核心素養(yǎng)視角下全國卷解析幾何命題特點分析

廣東 于 濤

自提出核心素養(yǎng)的總體框架和基本內(nèi)涵以來，高考評價體系就開始經(jīng)歷從能力立意到素養(yǎng)導(dǎo)向的歷史性轉(zhuǎn)變，解析幾何作為高考重點考查的內(nèi)容也被賦予了新的含義.結(jié)合數(shù)學(xué)核心素養(yǎng)與2018年《考試說明》來看，2018年全國卷對解析幾何的考查，注重基礎(chǔ)知識的鞏固與理解，主要考查直線與圓錐曲線的基本概念和簡單性質(zhì)，重點考查直線與圓錐曲線的位置關(guān)系；注重學(xué)科思維的考查，如運動與變化的基本觀點和用代數(shù)研究幾何的基本方法等；強調(diào)思想方法的考查，如數(shù)形結(jié)合、轉(zhuǎn)化與化歸、特殊與一般等思想方法；突出兩種能力的考查，即邏輯推理能力和運算求解能力；融入了直觀想象、數(shù)學(xué)抽象、數(shù)學(xué)運算、邏輯推理等數(shù)學(xué)核心素養(yǎng).

下面，筆者將結(jié)合數(shù)學(xué)核心素養(yǎng)的命題導(dǎo)向?qū)?018年全國卷解析幾何的命題特點進行分析.

1 解析幾何命題特點分析

縱觀2018年全國卷解析幾何的試題編排，試題數(shù)量穩(wěn)定，均為2-3道選填，1道解答，其中選填分布位置穩(wěn)定，1題屬于基礎(chǔ)題，1-2題屬于中高檔題，文理同題比例較往年有所提升.從考查曲線類型來看，4種曲線分布均勻，解答題集中在橢圓或拋物線.

1.1 注重學(xué)科基礎(chǔ)，凸顯直觀想象素養(yǎng)

直觀想象素養(yǎng)包括借助圖形感知認識事物，分析理解問題，通過建立形與數(shù)的聯(lián)系，探索問題的求解思路，也包括數(shù)學(xué)直覺思維，進行“以圖代證”的“正確”猜想.解析幾何高考命題注重對基本概念和幾何性質(zhì)等基礎(chǔ)知識的考查，如2018年Ⅰ卷文4，Ⅱ卷文6、理5都以基礎(chǔ)知識為考查核心.高考命題還強調(diào)對基本技能、基本思想和基本活動經(jīng)驗的考查，如2018年Ⅰ卷文15，Ⅲ卷文10在注重“四基”的同時，凸顯了直觀想象素養(yǎng).

例1.(2018·全國卷Ⅰ文·15)直線y=x+1與圓x2+y2+2y-3=0交于A，B兩點，則|AB|=________．

【點評】 試題精心設(shè)計了“特殊位置”的直線與圓，使得題目在解答過程中，既可以按照圓錐曲線弦長問題的基本方法求解，又可以結(jié)合圓的幾何性質(zhì)求解，還可以借助圖形“以圖代算”，直接求解，體現(xiàn)了“先畫圖，再分析、求解”的基本活動經(jīng)驗的重要性，有效地考查了學(xué)生的直觀想象素養(yǎng).

1.2 注重學(xué)科思維，凸顯數(shù)學(xué)抽象素養(yǎng)

數(shù)學(xué)抽象素養(yǎng)包括對數(shù)量關(guān)系與空間形式的抽象概括能力，也包括舍棄事物非本質(zhì)的屬性，揭示其本質(zhì)屬性的思維能力等.解析幾何用代數(shù)的方法研究圖形的幾何性質(zhì)，“代數(shù)”是研究工具，“幾何”是研究對象，問題的解決始于“幾何”，終于“幾何”.事實上，“幾何”也可以作為研究工具，全面地體現(xiàn)了解析幾何的學(xué)科思維.如2018年Ⅰ卷理11，Ⅱ卷文11、理12，Ⅲ卷理11都可以從代數(shù)、幾何兩個角度進行問題的求解.幾何解法需要經(jīng)歷數(shù)學(xué)抽象的過程，將題目曲線的基本概念、幾何性質(zhì)等條件信息進行圖形化翻譯后，抽象出題意蘊含的幾何圖形，凸顯了數(shù)學(xué)抽象素養(yǎng).

( )

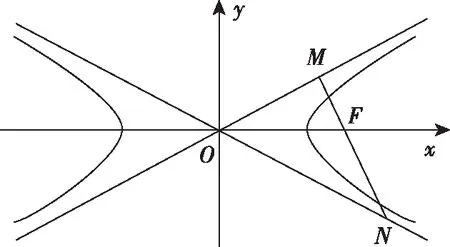
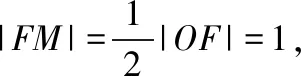
【點評】 試題把直角三角形與雙曲線的中心、漸近線有機整合，構(gòu)建了數(shù)形結(jié)合的環(huán)境，為不同能力的學(xué)生提供了方法選擇的空間，充分體現(xiàn)了解析幾何的學(xué)科思維：代數(shù)、幾何兩條路.試題解法的多樣性體現(xiàn)了思維的靈活性，代數(shù)解法思維量小，運算量大，起點低，落點高；幾何解法思維量大，運算量小，起點高，落點低.其中，幾何解法從大量信息中抽象出Rt△OMN,Rt△OMF,△OFN三個三角形，極大地簡化了運算量.要在“繁雜”的情境中抽象出“簡單”的數(shù)學(xué)對象，需要很好的數(shù)學(xué)抽象素養(yǎng).

1.3 強調(diào)多想少算，凸顯數(shù)學(xué)運算素養(yǎng)

數(shù)學(xué)運算素養(yǎng)包括理解運算對象，探究運算思路，選擇運算方法，設(shè)計運算程序等一系列過程中的思維能力，也包括掌握運算法則，求得運算結(jié)果等過程中遇到障礙調(diào)整運算的能力，以及敢算的勇氣和能算的信心.解析幾何試題考查以含字母的式子的運算為主，題目設(shè)置平穩(wěn)，容易上手，注重幾何問題解析化，力求人人可算，卻不一定能算、巧算.解題時必須進行認真的辨別、探索和選擇，做到多想少算，凸顯數(shù)學(xué)運算素養(yǎng).

【點評】 試題給定橢圓的方程，創(chuàng)設(shè)了橢圓動弦AB的中點在橢圓半通徑(x軸上方)上運動的情境.題目第(Ⅰ)問的兩個解題思路運算量差別巨大，解答時需要弄清命題背景，選擇恰當?shù)倪\算方法.題目第(Ⅱ)問增加了條件，信息較多，解題時可按照題目條件出現(xiàn)的順序進行“直譯”，以此來理清運算思路.三個環(huán)節(jié)的運算對象，對運算能力的要求逐步提高，每個環(huán)節(jié)的計算錯誤，都會導(dǎo)致后續(xù)解答的錯誤，強調(diào)了運算的準確性.試題的兩問從不同側(cè)面全面地考查了數(shù)學(xué)運算素養(yǎng).

1.4 注重合理轉(zhuǎn)化，凸顯邏輯推理素養(yǎng)

邏輯推理素養(yǎng)包括從一些事實和命題出發(fā)，推理論證其他命題的思維能力，也包括掌握推理的基本形式和規(guī)則，探索和表述論證過程，學(xué)會有邏輯地思考問題等.全國卷解析幾何試題設(shè)問簡明扼要，強調(diào)對幾何條件的等價轉(zhuǎn)化，解題時需根據(jù)具體情境廣泛地聯(lián)系相關(guān)知識，進行合理轉(zhuǎn)化，探索最佳論證過程.如2018年Ⅰ卷文20、理19，Ⅲ卷文8、理6都需進行合理轉(zhuǎn)化，凸顯了邏輯推理素養(yǎng).

(Ⅰ)當l與x軸垂直時，求直線AM的方程；

(Ⅱ)設(shè)O為坐標原點，證明：∠OMA=∠OMB.

(Ⅱ)要證明∠OMA=∠OMB，需要將其轉(zhuǎn)化為等價的代數(shù)關(guān)系，設(shè)A(xA,yA),B(xB,yB)，如圖，聯(lián)系不同的知識，有如下轉(zhuǎn)化方式.

方式1：由直線MA和直線MB關(guān)于x軸對稱，得kMA+kMB=0；

方式2：過O作直線MA,MB的垂線，垂足分別為D,E.由OM是∠AMB的角平分線，得dO-lMA=dO-lMB,即|OD|=|OE|；

方式3：記直線MA,MB與y軸的交點分別為G,H.優(yōu)化方式2，由△OMG≌△OMH，得|OG|=|OH|；

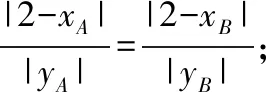
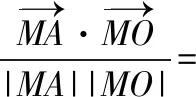
【點評】 試題以動弦(焦點弦)和定點(點M)構(gòu)造出運動與變化的情景，以圖形變化中的幾何不變性為命題背景，突出考查了幾何問題“解析化”的基本方法.設(shè)問的等價轉(zhuǎn)化過程體現(xiàn)了分析法的應(yīng)用，有效地考查了邏輯推理的基本形式，由形到數(shù)的轉(zhuǎn)化體現(xiàn)了數(shù)形結(jié)合的思想方法，8種轉(zhuǎn)化方式以方式1最佳，方式3，5次之，其余轉(zhuǎn)化方式或運算量巨大，或思路狹窄，多種轉(zhuǎn)化方式的探索與選擇，凸顯了邏輯推理的思維能力，試題多角度、多層次地考查了邏輯推理素養(yǎng).

1.5 注重學(xué)科規(guī)律，凸顯探究創(chuàng)新素養(yǎng)

探究創(chuàng)新素養(yǎng)包括發(fā)現(xiàn)、提出問題的意識和眼光，綜合與靈活運用所學(xué)知識、方法的能力，也包括能創(chuàng)造性地解決問題等.解析幾何有許多優(yōu)美的幾何性質(zhì)，高考命題也常以某個性質(zhì)為背景，或直接應(yīng)用，或探究證明，注重學(xué)科規(guī)律，如下表.

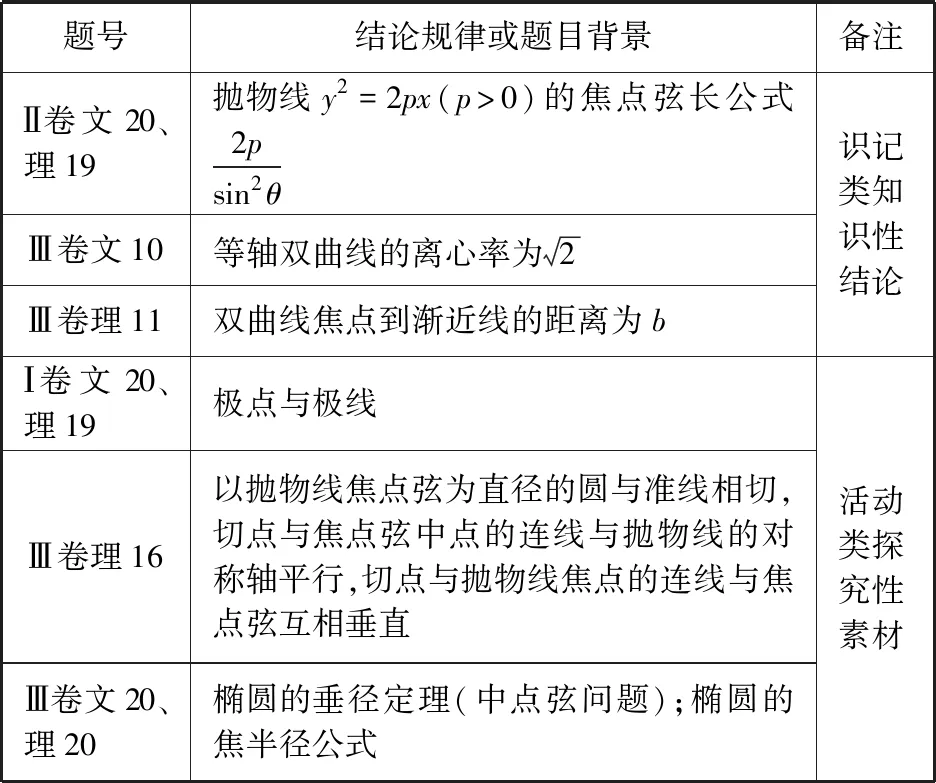
2018年全國卷解析幾何試題的結(jié)論規(guī)律或題目背景

知識性結(jié)論的積累和應(yīng)用，有助于減少解題的運算量.由探究性素材得到或體現(xiàn)的結(jié)論，要知其然，知其所以然.教學(xué)中可圍繞這些問題展開自主探究、合作研究，培養(yǎng)學(xué)生發(fā)現(xiàn)和提出有意義的數(shù)學(xué)問題的意識，提升學(xué)生猜想合理數(shù)學(xué)結(jié)論的能力，發(fā)展學(xué)生的探究創(chuàng)新素養(yǎng).

例5.(2018·全國卷Ⅲ理·16)已知點M(-1,1)和拋物線C:y2=4x，過C的焦點且斜率為k的直線與C交于A,B兩點.若∠AMB=90°，則k=________．

思路2如圖，若發(fā)現(xiàn)或知道DM∥x軸(D是AB的中點)，則由yA+yB=2yD=2得到關(guān)于k的方程.

【點評】 試題以拋物線焦點弦的幾何性質(zhì)為命題背景，思路1是常見的解析化思維，運算量很大，間接的從代數(shù)角度證明了思路2，3中的結(jié)論；思路2，3體現(xiàn)了“幾何多一點，代數(shù)少一點”的學(xué)科思維，根據(jù)幾何猜想或證明相應(yīng)結(jié)論，凸顯了直觀想象素養(yǎng).試題可向教學(xué)延伸，進行拋物線平面幾何性質(zhì)的探究，其性質(zhì)多達十余條(限于篇幅，不一一羅列)，凸顯了注重探究創(chuàng)新的命題導(dǎo)向.

2 解析幾何復(fù)習(xí)備考建議

2.1 牢固基礎(chǔ)知識

復(fù)習(xí)備考要用好《考試說明》和教材.《考試說明》能給復(fù)習(xí)備考以方向性的指導(dǎo)，例如《考試說明》中與圓有關(guān)的要求，使用的都是“掌握”“能”這樣要求較高的行為動詞，因此，要重視對圓的復(fù)習(xí)，也要重視與圓有關(guān)的綜合問題的復(fù)習(xí)，如2018年Ⅱ卷文20、理19就涉及對拋物線與圓的綜合考查.關(guān)于圓錐曲線的知識要求，則強調(diào)概念、性質(zhì)兩手抓，教學(xué)時可以幫助學(xué)生構(gòu)建知識體系，積累易錯點，力求夯實基礎(chǔ)，突出重點.教材是高考命題的素材源泉，復(fù)習(xí)時可以對教材中的經(jīng)典例題、習(xí)題進行變式、拓展和深化，強化知識的同時，突出對基本技能、基本思想、基本活動經(jīng)驗的復(fù)習(xí)，扎實學(xué)科基礎(chǔ)，為素養(yǎng)的養(yǎng)成和發(fā)展做好條件準備.

2.2 重視思想方法

數(shù)學(xué)思想方法引領(lǐng)著數(shù)學(xué)知識與數(shù)學(xué)方法的應(yīng)用，能幫助學(xué)生提升思維能力.《考試說明》中與解析幾何有關(guān)的要求，明確提出：“理解數(shù)形結(jié)合的思想”，“數(shù)”與“形”是解析幾何的本質(zhì)體現(xiàn)，代數(shù)好想不好算，幾何好算不好想，幾何條件挖掘越充分，代數(shù)表征就越簡潔，運算量就越小，文中例題均有所體現(xiàn).因此，數(shù)形結(jié)合不僅要以形助數(shù)，更要重視代數(shù)、幾何兩條路，培養(yǎng)學(xué)生先幾何后代數(shù)的思維習(xí)慣，力求每個題目都從代數(shù)、幾何兩種角度進行解法研究.全國卷解析幾何試題涉及的“幾何”多與特殊三角形、相似三角形、解三角形等幾何知識有關(guān)，教學(xué)時可以注重經(jīng)驗的積累.對于其它思想方法，要特別重視轉(zhuǎn)化與化歸的思想，教學(xué)中對每個幾何關(guān)系的轉(zhuǎn)化，都要讓學(xué)生聯(lián)系所學(xué)，盡量多的等價轉(zhuǎn)化，然后再比較不同轉(zhuǎn)化方式的優(yōu)劣，如文中例4，以此來培養(yǎng)學(xué)生形成思維中的慣性觀念，以及根據(jù)題目條件進行合理轉(zhuǎn)化的能力.除此以外，在有關(guān)定值、定點等存在性和探究性問題時，要特別重視特殊與一般的思想，解題從特殊情形入手，先通過“特殊”找到可能存在的結(jié)果，再對結(jié)果進行一般情形的驗證，做到先特殊后一般，四兩撥千斤.其中，有關(guān)斜率存在與不存在的分類討論，也可歸入特殊與一般的教學(xué).應(yīng)用思想方法能力的提升，也標志著數(shù)學(xué)核心素養(yǎng)的發(fā)展.

2.3 強化兩種能力

邏輯推理能力與運算求解能力是解析幾何掙不脫躲不過的能力要求，兩種能力并不孤立，邏輯推理能力能幫助學(xué)生通過對可行解題思路的預(yù)估，評價運算量的大小，引導(dǎo)學(xué)生選擇運算量較小的解題方式，因此，教學(xué)中要注重以邏輯推理助力運算求解.反過來，過硬的運算求解能力，能讓學(xué)生大膽設(shè)取字母，積極運算，能促進學(xué)生邏輯推理的暢順.二者相輔相成，缺一不可，促進邏輯推理素養(yǎng)和數(shù)學(xué)運算素養(yǎng)的共同提升.

2.4 關(guān)注探究創(chuàng)新

素養(yǎng)導(dǎo)向的高考命題以新背景、新情境、新信息等方式，考查學(xué)生的科學(xué)探究能力和創(chuàng)新能力.教學(xué)中要將符合命題導(dǎo)向的高考試題向教學(xué)延伸，如文中的例4、例5，不論是對試題多種解法展開探究，還是對試題高等幾何背景、拋物線平面幾何性質(zhì)的挖掘與學(xué)習(xí)，都是激發(fā)學(xué)生學(xué)習(xí)興趣，培養(yǎng)主觀能動性，發(fā)展創(chuàng)新能力的過程.需要指出，對探究得到的結(jié)論或性質(zhì)，需要讓學(xué)生明確其證明方法，經(jīng)歷其推導(dǎo)過程，以此來促進學(xué)生科學(xué)態(tài)度的形成，以及科學(xué)素養(yǎng)的提升.