從培養學生科學思維的視角例談數模建構

朱淑芳

(福建省漳州市第五中學 漳州 363000)

在教學中滲透科學思維能力的培養尤為必要，而數學模型作為揭示生命現象的特殊的呈現形式，是將原型的本質特征用數學語言構建而成的邏輯嚴密的數學過程或符號。本文以數模建構為抓手，引導學生進行改造、修正和完善，在建模、析模過程中達成思維的有序展開，使數模建構成為培養學生科學思維能力、提升生物學核心素養的有效途徑。

1 改造模型，促成知識內化升華，培養批判性思維

批判性思維能力是能夠質疑、解釋、分析和自我校準的能力[1]。數學模型是對生物學知識的精練簡化，往往是學生解釋分析問題的重要載體。在建模過程中，引導學生提取原有模型承載的知識信息，深挖掘、細分析，在新的條件下完成模型改造，讓被利用的先前知識根據具體情境的變異性得以重新建構，實現原有知識的內化、升華，讓學生在思維碰撞和問題解決的過程中，提升批判性思維的能力。

例如，學生對捕食關系的數學模型的認知是以種群數量和時間建立起來的坐標圖(見教材第73頁“資料分析”中“猞猁和雪兔種群數量的變化曲線”)。在這個模型里承載著這樣的信息： 被捕食者和捕食者之間呈現“先增加者先減少，后增加者后減少”的不同步變化。在授課過程中，鼓勵學生轉變思維，對該模型進行改造： 構建以被捕食者種群數量為橫坐標，以捕食者種群數量為縱坐標的新模型(圖1)。構建后，設置問題進一步自我校準： 若將封閉環以P2為橫軸、N2為縱軸，劃分為①②③④共4個區間，每個區間分別對應原坐標圖中的哪個區段？改造后的模型能體現“先增加者先減少,后增加者后減少”這種變化規律嗎？同時，可引導學生對錯誤觀點“P3代表捕食者的K值，N3代表被捕食者的K值”提出質疑并進行解釋分析： 從圖1封閉環的變化趨勢可以看出，捕食者和被捕食者在相互作用過程中，數量在N2和P2水平上保持動態平衡。所以，P2和N2才是捕食者和被捕食者的K值。

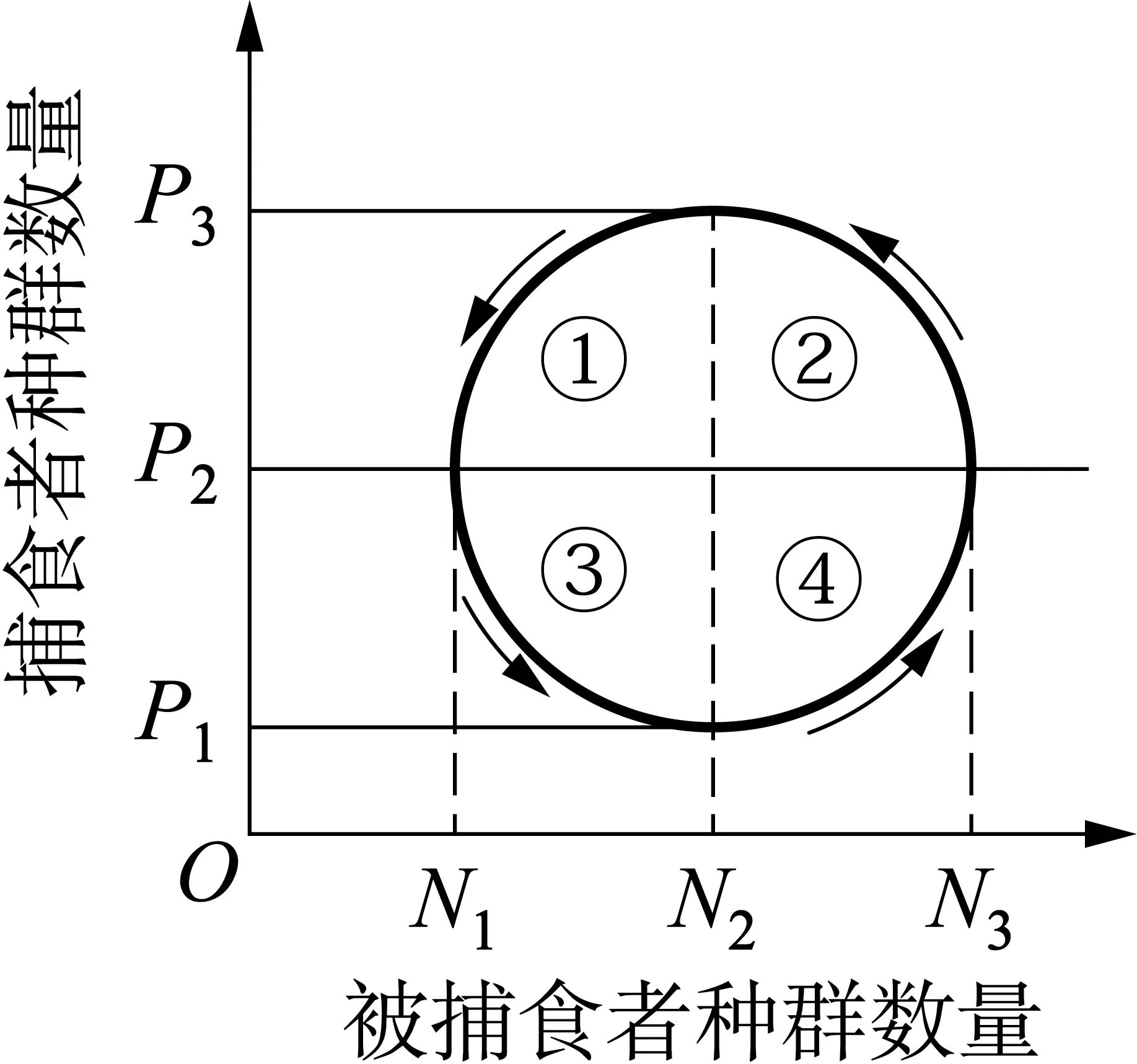
圖1 捕食者和被捕食者種群數量變化關系

綜上可見，在對模型的改造重建過程中，伴隨著對問題的抽絲剝繭，理性的辨析使學生在熟悉內容和陌生問題間實現有效轉化升華，促成思維遷移和問題解決，一定程度上培養和鍛煉學生的批判性思維。

2 修正模型，實現技能遷移應用，提升演繹推理能力

演繹推理是以一般性知識判斷為前提，推出個別的、具體的知識結論的推理過程，是重要的科學思維方式[2]。眾所周知，學生對于遺傳學“雜合子Aa(親代)連續自交，求第n代基因型的比例”“Aa連續自交并逐代淘汰隱性個體，求第n代基因型的比例”這類經典問題常望而生畏。但由于其推導過程所涉及的建模方法是突破有關基因分離定律某些重點題型的好方法，也是培養學生演繹推理能力的有效“推手”，所以一直很受關注。

例如，在分析這類題型時，引導學生從正常情況展開建模，即逐代寫出Aa連續自交(不淘汰)時各基因型的比例(F1代： 1/4AA，1/2Aa，1/4aa；F2代： 3/8AA，1/4Aa，3/8aa……)，分析至F3代，依據規律便可構建出相應的函數模型： 第n代雜合子的比例等于(1/2)n。在這基礎上，結合設定的限制條件(逐代淘汰隱性個體)，引導學生沿著原有思維軌跡繼續推理分析時就會發現： 逐代淘汰隱性個體會影響到每一代非隱性個體基因型在總群體中所占的比例(圖2)，這時學生自然會領悟到： 當原有模型已經不再適用于新情境時，就必須結合新信息給予修正，在思辨過程中演繹推理出正確的模型： Aa連續自交(淘汰隱性個體)，第n代雜合子的比例應為2/(2n+1)。

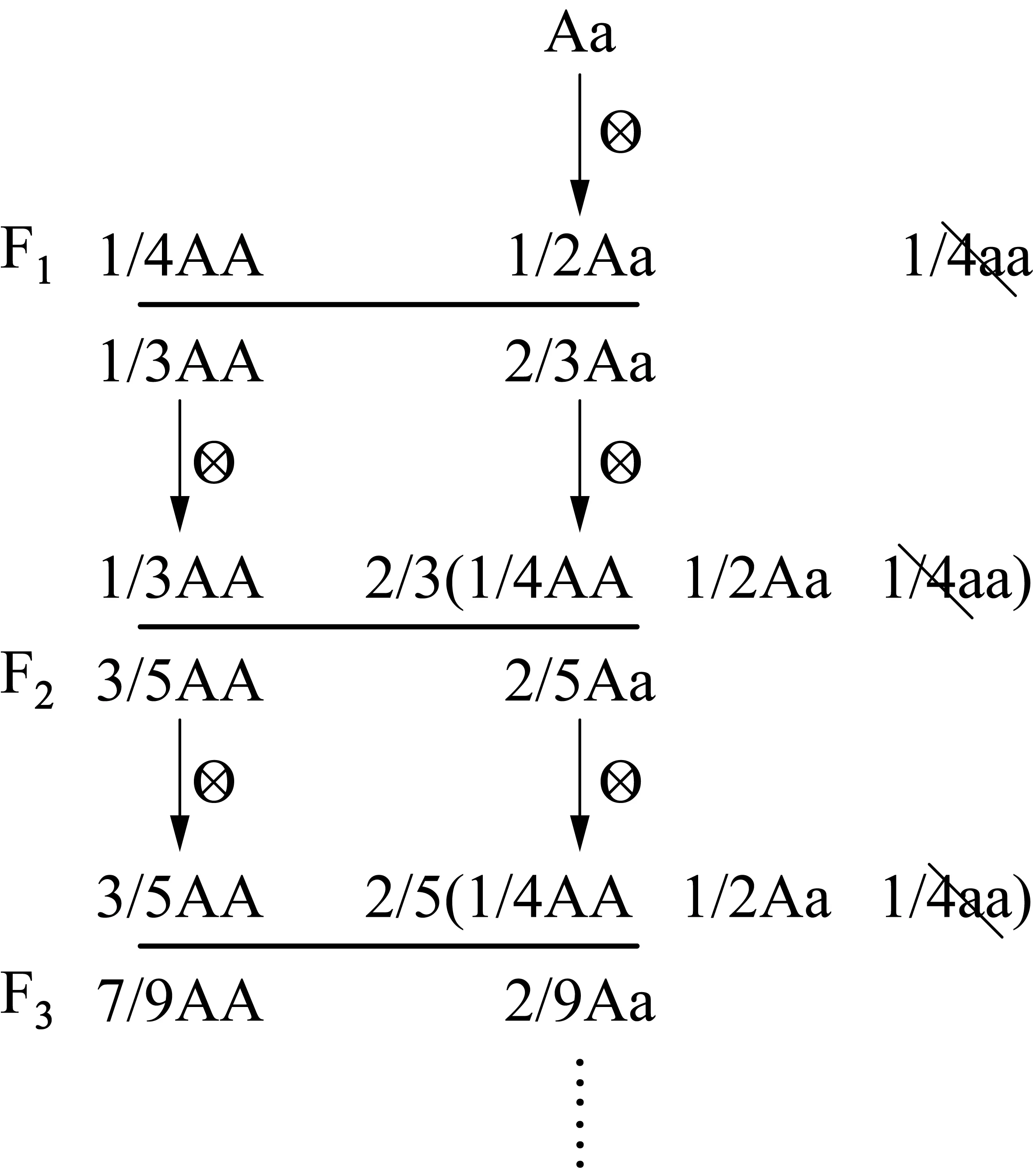
圖2 Aa連續自交(淘汰aa)后代基因型頻率的變化

在模型的修正過程中，促成了學生從一般規律的理解應用到學會運用新規律來檢驗、鞏固新知識的飛躍，不僅實現了數學知識技能在生物學領域的遷移應用。同時,也讓學科素養和能力培養在建模過程中得到滲透和提升。

3 完善模型，達成知識遷移拓展，提高概括歸納能力

數學模型可以用來描述事物本質和變化規律，在組織教學過程中，教師可有意識地引導學生對模型進行完善充實，不僅擴充了模型的知識承載量，同時也培養了學生透過現象揭示本質的洞察力和對事物變化規律的準確概括歸納能力[3]。

例如，在教材(必修2)“孟德爾豌豆雜交實驗(一)”一節“性狀分離比”的模擬實驗中，教材只要求完成一組模擬實驗并設計相應的數據統計表(表1)。在這個實驗中，模擬雌雄生殖器官的甲乙兩袋內D配子和d配子數量相同(均為15個)，且甲乙兩袋內配子總數相等(均為30個)。但單純完成這組模擬實驗，并不能有效達成體驗孟德爾假說、理解分離定律實質的目的。因此，設置如下問題： 如果甲乙兩袋內D、d配子數相同，但兩袋內配子總數不同，對實驗結果有影響嗎？如果甲乙兩袋內D、d配子數不同，但兩袋內配子總數相同，又會產生什么樣的結果呢？引導學生根據問題進行拓展實驗并完善原有圖表模型，最終獲得另外2組數據(表2、表3)。

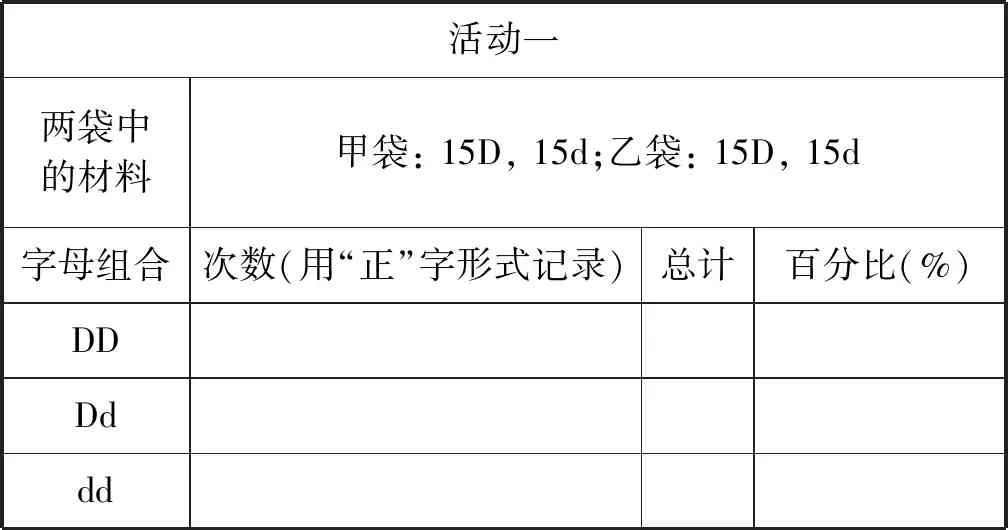
表1 孟德爾性狀分離比模擬實驗小組記錄數據統計表(活動1)

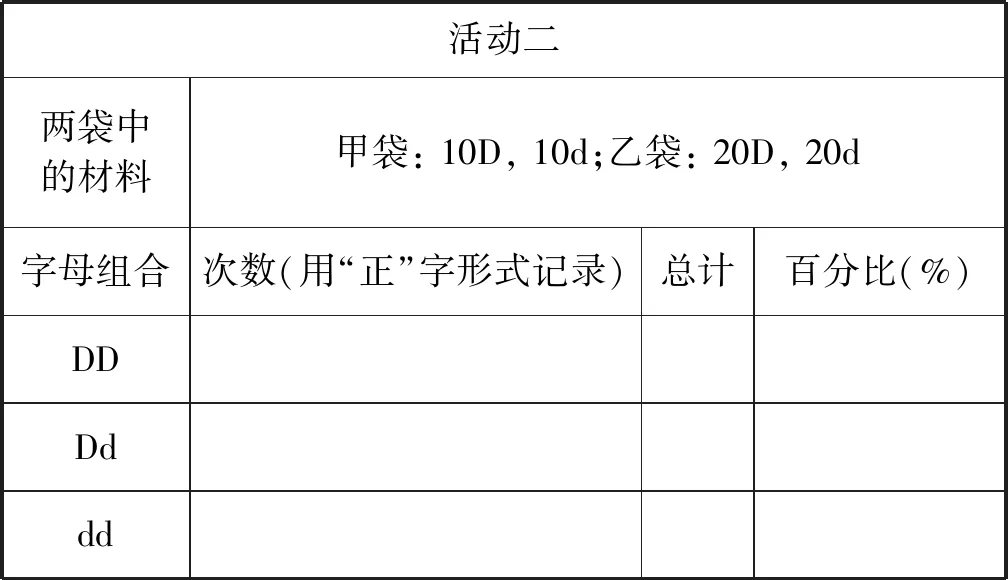
表2 孟德爾性狀分離比模擬實驗小組記錄數據統計表(活動2)

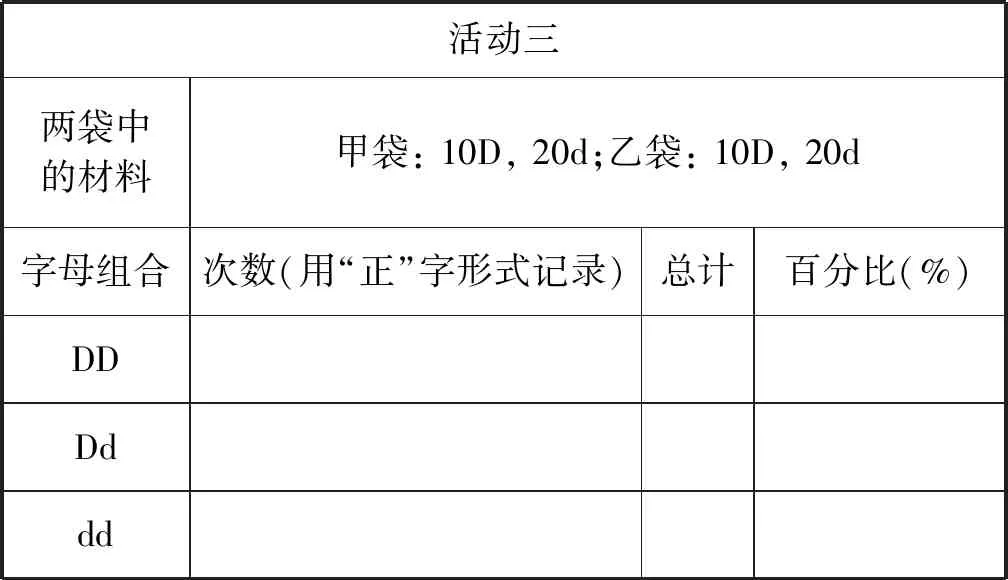
表3 孟德爾性狀分離比模擬實驗小組記錄數據統計表(活動3)

通過數據處理、模型(3個統計表)對比和歸納分析，學生會發現，活動1、 2的數據統計結果DD∶Dd∶dd接近于1∶2∶1；而活動3中該數據遠偏離1∶2∶1。

學生很快會意識到形成3∶1性狀分離比的關鍵之一是雜合子產生的2種不同的配子比例要相等，進一步厘清了分離定律的實質。