合情推理在豌豆雜交實驗中的運用

武佳佳 李 廣 劉赫健

(1 山西省忻州市第一中學 忻州 034000； 2 上海財經大學信息管理與工程學院 上海 200433； 3 北京航天航空大學北航學院 北京 102206)

科學假說是以一定的經驗材料和科學事實為依據，對預期事物所做出的推測性解釋。而演繹過程則是從一些假設的命題出發，運用邏輯的規則，導出另一命題的過程。而假說的得出往往要經過觀察、分析、比較、聯想，再經過歸納和類比，也就是我們常說的合情推理[1]。

科學思維是生物學科中培養核心素養很重要的方面。在教學過程中，不論是對現實生物學問題的數學抽象還是對復雜生物學問題的理想化數學模型的建立，都可以作為培養學生科學思維的載體。在豌豆雜交實驗的教學過程中，我們往往重視假說演繹思想的滲透。的確演繹推理是證明科學結論、建立科學體系的重要思維過程，但科學結論、新思路等的發現，主要靠合情推理。合情推理和演繹推理是推理思維活動的兩種基本形式。在教學實踐過程中，豌豆的雜交實驗不僅可以訓練學生的演繹推理，同時也是訓練合情推理的好素材。

1 歸納推理和演繹推理

歸納推理是從特定事實向一般事實推理的過程，是從實驗重復中建立起某種確定性或規律性結論的一種認知策略。運用好歸納推理展開教學，有利于激發學生參與學習的積極性，也有助于科學思維在學科教學中的落地。

實例一： 豌豆的高莖對矮莖為顯性。讓雜合的高莖豌豆連續自交，F5播種后長出的高莖植株中純合體所占的比例多少？(注： 豌豆的高莖基因和矮莖基因分別用A和a來表示，其中A對a完全顯性，不考慮基因突變和其他自然選擇的情況，同時所有個體都可以存活，以下實例假定條件與該實例相同。)

分析： 要求解雜合體連續自交五代后高莖植株中純合體所占的比例，首先計算由親本到子一代中的三種基因型的比例，再計算高莖植株中純合體所占的比例，同理直到第五代，繪制表格如下(表1)。

根據表格，得出F5播種后長出的高莖植株中純合體所占的比例為31/64。通過分析表格中數據，歸納推理可以得出P(AA)和P(aa)相等的結論。進一步發現，子代的前5代雜合體的概率都等于相應自交次數1/2的指數函數(即1/2n)，由此猜想，雜合體連續自交n代，雜合體的概率是1/2n。

上述過程也是數學建模的過程，數學模型是用來描述一個系統或其性質的數學形式，是一種用符號、公式、圖象等數學語言表現研究現象、特征和狀況的研究方法[2]。在繁雜的生物學原型基礎上抽離出的一個簡化、理想化的數學模型，有助于學生系統地、完整地學習和理解新知識。但在模型基礎上，經過數學分析得出的結論必須與具體的生物學過程相結合并加以檢驗[3]。所以雜合體連續自交n代，得出雜合體概率是1/2n的結論，還需要結合假定條件下的生物學過程加以分析驗證。

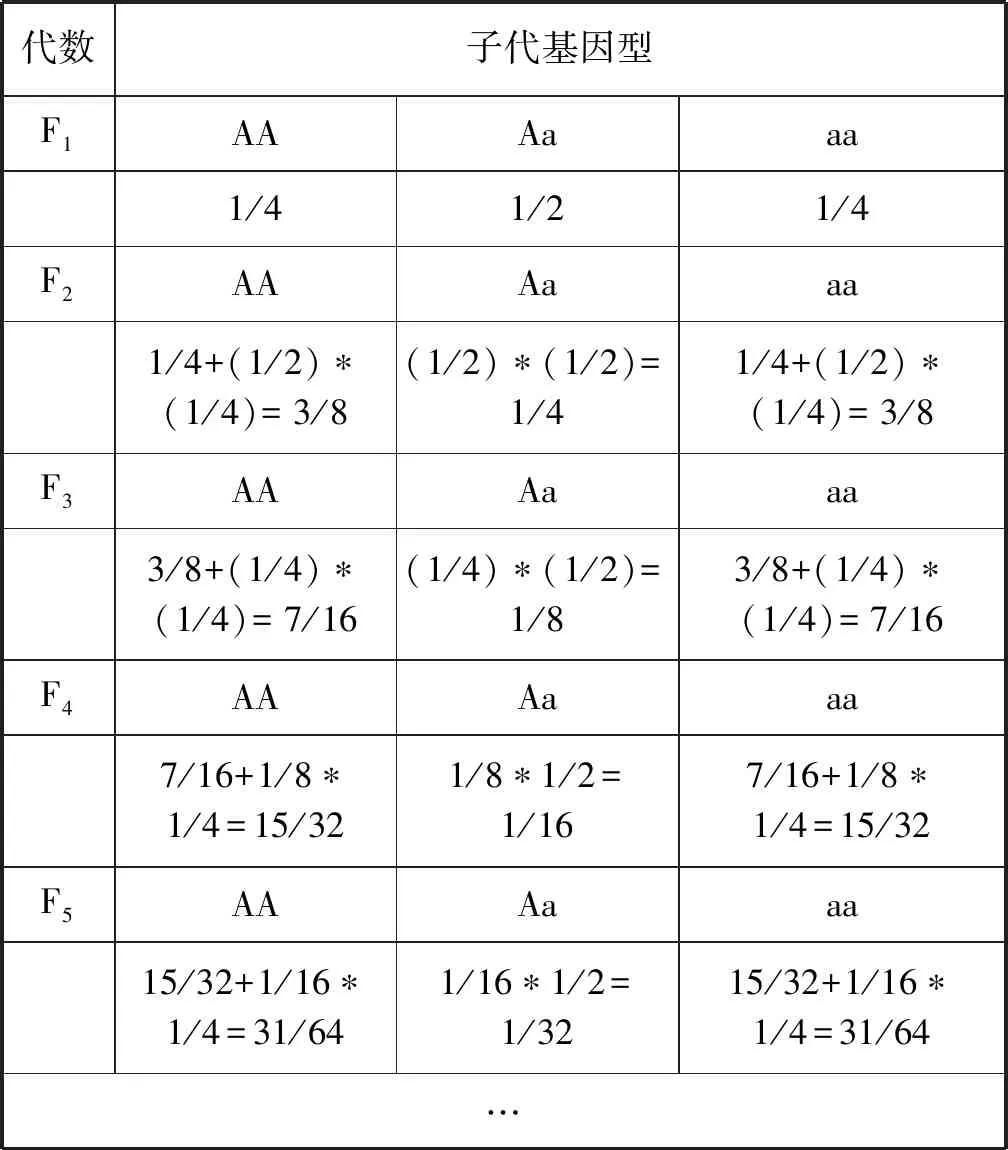
表1 雜合體(Aa)連續自交代數和子代基因型所占比例

根據生物學遺傳規律，Aa逐代自交(不考慮個體死亡、遷出遷入等)，后代會出現AA、 Aa、 aa三種基因型的個體，AA和aa是純合體，純合體自交后代不發生性狀分離，仍為純合體。而每自交一代雜合體的概率在原來的基礎上再乘以1/2，所以P(Aa)=1/2n(n為Fn中的n，n是正整數),基因型為AA的個體與基因型為aa的個體數量相等，故P(AA)=P(aa)=(1-1/2n)/2(n為Fn中的n，n是正整數)。P(Aa)=1/2n(n為Fn中的n，n是正整數),基因型為AA的個體與基因型為aa的個體數量相等，故P(AA)=P(aa)=(1-1/2n)/2(n為Fn中的n，n是正整數)。

演繹推理： 當n→∞,子代中純合體所占的比例接近于1，顯性純合體或隱性純合體所占比例接近于1/2。雜合體的比例接近于0。這樣就可以很好地解釋教材中孟德爾一對相對性狀的雜交實驗中親本高莖是純合體的原因。

2 類比推理和合情推理

在合情推理的過程中，除了歸納，往往還應用類比。遺傳學家薩頓運用類比的思想提出了基因與染色體的平行關系，仿生學中許多發明的最初構想都是類比生物機制得到的。豌豆的雜交實驗同樣也可以訓練學生的類比思想。

實例二： 豌豆的高莖對矮莖為顯性。讓雜合的高莖豌豆連續自交，F5播種后淘汰矮莖類型，則長出的高莖植株中純合體占的比例是多少？

分析： 根據實例一得出的結論： P(Aa)=1/2n，P(AA)=P(aa)=(1-1/2n)/2。所以在淘汰隱性純合子之后，顯性純合子在全部植株中所占比例為： [(1-1/2n)/2]/[(1-1/2n)/2+(1/2n)]=(2n-1)/(2n+1)。題目中n=5，則顯性純合子所占比例為31/33。

實例三： 豌豆的高莖對矮莖為顯性，讓雜合高莖豌豆連續自交并逐代淘汰矮莖豌豆類型，F5播種后長出的植株中高莖純合體所占比例為多少？

分析： 如同實例一采用的做法，分別計算讓雜合高莖豌豆連續自交并逐代淘汰矮莖豌豆后，每一代中基因型分別為AA、 Aa、 aa各自的比例，再計算去掉矮莖之后的比例，見表2。

從實例二和實例三不難看出，第5代淘汰隱性個體和逐代淘汰隱性個體的結果是一樣的。故猜想： Aa自交n代第n代去掉aa，第n代P(AA)的大小與Aa自交n代每一代去掉aa，第n代P(AA)的大小相等。

關于Aa自交n代后第n代去掉aa，第n代P(AA)的大小，可根據實例一，演繹推理得出一個計算公式P(AA)=(2n-1)/(2n+1)。類比實例一和實例二，猜想實例三可能也有一個關于n的計算公式。

結合表2，F1中P(AA)=1/3，F2中P(AA)=3/5，F3中P(AA)=7/9，F4中P(AA)=15/17，F5中P(AA)=31/33，將Fn時P(AA)記作an。猜想Fn時，an(即P(AA))=(2n+1-2)/(2n+1)=(2n-1)/(2n+1)。根據生物學遺傳規律： a(n+1)=[an+(1-an)*1/4]/[an+(1-an)*1/4+(1-an)*1/2]，即a(n+1)=(3an+1)/(an+3)，且a1=1/3。

下面我們用數學歸納法證明此猜想。

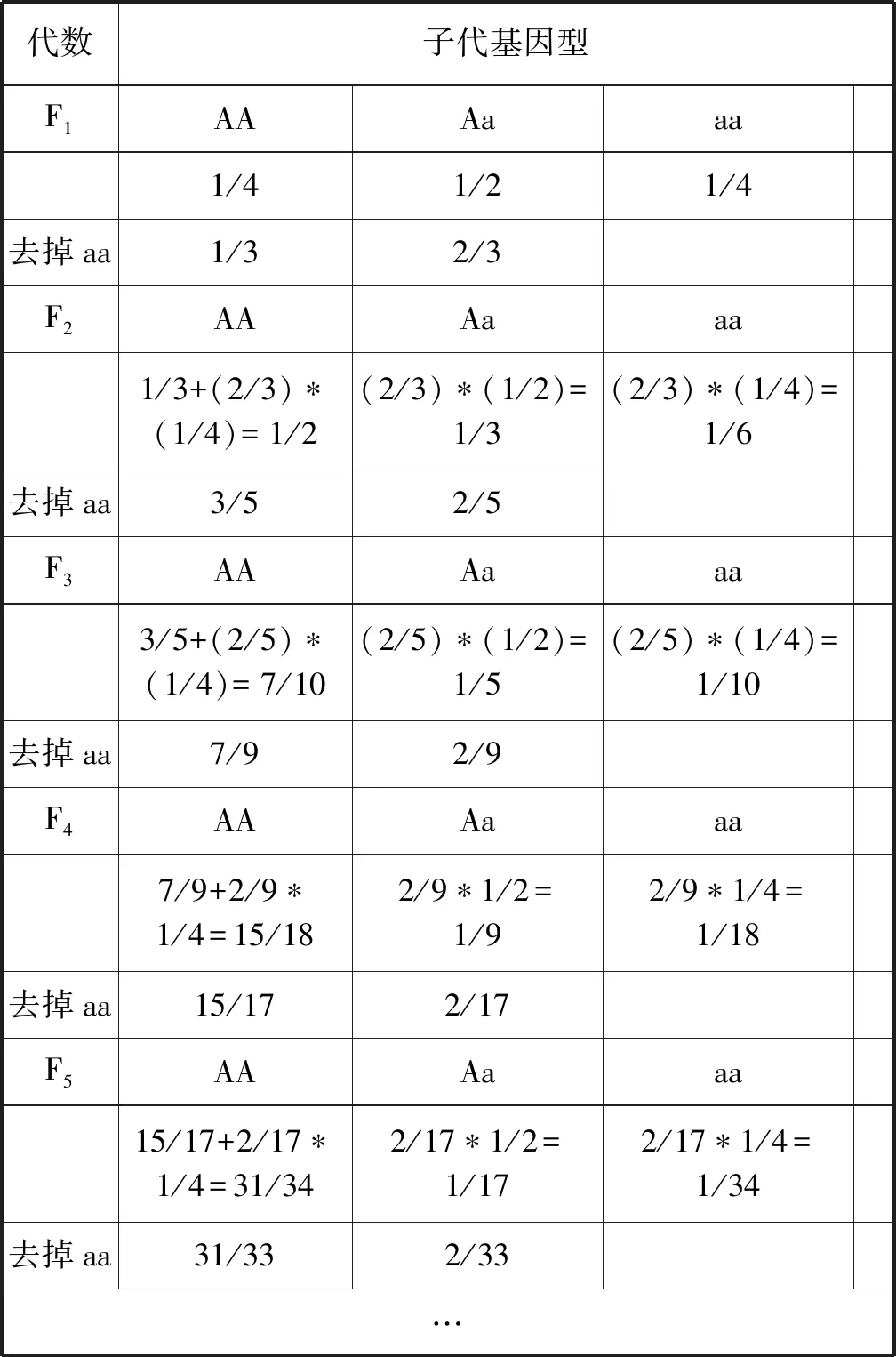
表2 雜合體(Aa)連續自交(逐代去掉aa)代數和子代基因型所占比例

(1) n=1時，a1=1/3，猜想顯然成立。

(2) 假設當n=k(n∈N*)時猜想成立，即ak=(2k-1)/(2k+1),那么a(k+1)=(3ak+1)/(ak+3)=[3(2k-1)/(2k+1)+1)]/[(2k-1)/(2k+1)+3]=(2k+1-1)/(2k+1+1)。

所以當n=k+1時猜想也成立。

根據(1)(2)，可知an=(2n-1)/(2n+1)對n∈N*都成立。

所以當Aa自交n代后第n代去掉aa，第n代P(AA)的值與Aa自交n代每一代去掉aa，第n代P(AA)的值相等。

3 小結

結合上面的實例，以豌豆雜交實驗為素材，可以很好地訓練學生的合情推理能力和演繹推理能力。合情推理和演繹推理作為推理的兩種基本形式，兩者是緊密聯系、相輔相成的。人們在認識世界的過程中，需要通過觀察實驗等獲得經驗，也需要部分到整體的歸納和特殊到特殊的類比，同時也需要將獲得的猜想加工和整理，使之條理化和系統化。合情推理和演繹推理分別在這兩個環節中扮演重要角色。