基于QPSO-SVR和聲發射信號的機械密封壽命預測*

(西南交通大學機械工程學院 四川成都 610031)

機械密封作為大型旋轉設備中必不可少的裝置，因其體積小、泄漏量小、可靠性高等優點，廣泛地應用于石油化工等過程工業大型旋轉設備[1]。據調查顯示，在旋轉設備中其使用率高達90%。機械密封的性能狀態直接影響生產過程中的安全和效率，因此對機械密封進行狀態監測和壽命預測尤為迫切。

長期以來，眾多學者致力于機械產品性能監測方法的研究，而壽命預測是機械密封健康監測中的重要組成部分，它對避免重大事故的發生和預知性維修具有重大意義。常用的壽命預測方法有2種：一是基于產品失效機制進行壽命預測；二是在數據驅動下通過機器學習或人工智能算法，對觀測數據進行深度分析、挖掘及融合，得到產品的退化曲線，從而得到剩余使用壽命。由于機械密封涂層摩擦副的退化過程很難建立相應的物理失效模型，考慮到機械密封失效機制是基于累積損傷的退化過程，通過得到完整的壽命周期數據，確定失效閾值，就可以使用支持向量回歸預測模型建立退化模型[2-3]。

聲發射檢測方法是一種無損檢測方法，作為非接觸式傳感方式，被大量應用于工業現場實時監測作業。聲發射實質上是應力波，是由于材料局部能量快速釋放而產生的瞬態彈性波[4]。CHOUDHURY和TANDON[5]利用聲發射參數對軸承故障進行了診斷和預測。單一的聲發射參數雖然分析速度較快，但是分析準確度低，易受環境影響[6-7]。

支持向量回歸(SVR)是近年發展起來的統計學習理論，具有泛化能力強、訓練時間短、全局優化和抗干擾能力強等優點，在工程領域有著廣闊的應用。傳統的參數選擇方法具有一定的盲目性，小幅的參數變化將會導致結果的巨大偏差[8-10]。面對大量數據樣本時，普通SVR算法的復雜度會大量增加，導致預測準確度和模型泛化能力急劇下降[11]。

針對上述問題，本文作者以金剛石涂層機械密封為研究對象，通過聲發射技術建立設備運轉時的聲發射信號與密封性能之間的關系，提出了基于聲發射特征融合的退化指標和QPSO-SVR壽命預測模型的機械密封剩余壽命預測方法。實驗證明，該模型能對機械密封壽命做出較好的預測，從而為機械密封壽命預測的工業應用提供了良好的技術支撐。

1 金剛石涂層機械密封壽命實驗

1.1 密封失效形式分析及檢測方式的選擇

機械密封失效成因包括化學損壞、熱損壞和機械損壞，分別體現為腐蝕、過熱和磨損[12]。文中實驗對象為金剛石涂層機械密封，它的退化過程實質上是涂層脫落和磨損，進而導致密封性能下降，最終導致密封泄漏量增大。聲發射技術是一種無損測量手段，可以在不破壞密封物理結構的情況下連續實時地監控密封運行狀態，并且涂層的磨損和脫落過程伴隨著大量的應力波釋放，而聲發射現象的實質正是應力波，所以采用聲發射技術建立設備運轉時的聲發射信號與密封性能之間的關系。

1.2 實驗裝置

實驗對象為金剛石涂層機械密封摩擦副，采用聲發射傳感器監測其聲發射信號。機械密封的金剛石涂層厚度為2～4 μm，電機轉速穩定在1 790 r/min。實驗時對機械密封施加100 N的軸向壓力，聲發射傳感器安裝在最靠近機械密封的表面，采樣頻率為2 MHz。

圖1所示為實驗中使用的金剛石涂層機械密封環。

圖1 金剛石涂層機械密封環

1.3 實驗結果

圖2、圖3是密封勻速旋轉時所測得的聲發射信號，其中包含了大量的噪聲，淹沒了有效信息。因此為了提高信噪比，突出壽命信息，將對信號采用小波降噪和特征提取。

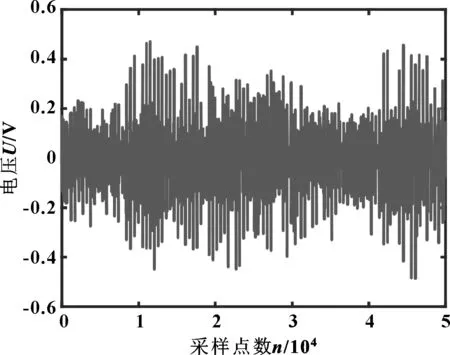
圖2 聲發射信號時域波形

圖3 聲發射信號頻域波形

2 研究方法

由于聲發射信號易受環境影響，信噪比較低，難以直接得出有效信息。采用傳統聲發射參數分析法結合KPCA，將特征進行優化，并且利用馬氏距離得出壽命信息，這樣不僅降低了特征維數，還削弱了特征之間的非線性相關程度。針對傳統SVR預測準確度低、預測效率低且泛化能力差的問題，提出QPSO優化SVR的預測模型，自適應進行參數尋優，對壽命信息進行有效利用，較之普通的SVR有更高的預測準確度。

2.1 特征選擇

聲發射參數分析法是利用聲發射信號的特征參數對聲發射源進行定性識別、定量評價[13]，主要是在時間域和頻率域內對信號進行放大、濾波、統計特征提取等。由于涂層密封的失效形式主要表現為涂層脫落和表面磨損，結合聲發射信號的參數分析法，采用的評價指標及評價意義如表1所示。

表1 聲發射特征選取

2.2 退化指標

馬氏距離是衡量服從同一分布且有著協方差矩陣的隨機變量之間的差異程度。假設共有m個樣本向量(X1,X2,......,Xm)，其中Σ為總體的協方差矩陣，則向量Xi與Xj之間的馬氏距離定義為

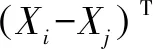
(1)

2.3 量子行為粒子群算法(QPSO)

量子行為粒子群算法是一種應用度廣、適應性高的優化算法。其主要思想是通過在解空間初始化一個粒子群，以適應度函數評價粒子的優劣，用最優個體更新迭代，最后得到一個全局最優解[14]。

假設一個包含m個粒子的粒子群在D維解空間中飛行，在t時刻，第i個粒子位置表示為Xi(t)=Xi,1(t),Xi,2(t),......,Xi,D(t)，其中i=1,2,......,m。第i個粒子在D維解空間中的歷史最優位置表示為Pi(t)=[Pi,1(t),Pi,2(t),......,Pi,D(t)]，群體的全局最優位置表示為G(t)=[G1(t),G2(t),......,GD(t)]，且G(t)=Pg(t)，其中g是全局最優位置粒子的下標，g∈1,2,......,m。個體最優位置的平均表達式為

(2)

對于最小化問題，目標函數值越小，對應的適應值越好，故第i個粒子的個體最優位置Pi(t)表達式為

(3)

群體的全局最優位置G(t)為

(4)

粒子位置進化方程為

Pi,jt+1=φj(t)·Pi,j(t)+1-φj(t)·Gj(t)φj(t)∈U0,1

(5)

Xi,jt+1=Pi,j(t)±α·Mbest(t)-Xi,j(t)·ln1/ui,j(t)ui,j(t)∈U0,1

(6)

其中，φj(t)、ui,j(t)為(0,1)區間均勻分布的隨機數，若ui,j(t)大于0.5，α前取負號，否則取正號。

2.4 支持向量回歸

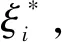
(7)

再引入懲罰參數c和拉格朗日乘子，對w、b求偏導，則可以將w和b的求解問題轉換為一個凸二次規劃問題：

(8)

選擇適當的核函數Kxi,x代替上式中的內積運算φ(xi),φ(xj)，即可構造出回歸函數：

(9)

支持向量回歸最大的特點是以統計學習理論為基礎，實現小樣本條件下的學習方法和統計規律，而且結構簡單，在機械密封壽命預測方面有一定的優越性。

2.5 量子行為粒子群算法優化支持向量回歸(QPSO-SVR)

傳統的SVR需要輸入懲罰參數c和核函數參數g，這2個參數與支持向量回歸的預測準確度息息相關。針對這種情況選用廣義交叉驗證(GCV)風險函數作為QPSO優化支持向量回歸的適應函數，通過目標函數最小化來選取漸進最優參數c和g。其主要步驟為

(1)對最佳懲罰參數和最佳和函數參數進行編碼；

(2)確定適應函數為CGV風險函數；

(3)初始化粒子群，確定迭代次數；

(4)輸入樣本數據，計算粒子的適應度；

(5)判斷粒子適應度是否達到要求，如果達到要求就進行解碼，如果未達到要求重新計算粒子群的平均最優位置，繼續進行迭代，直至滿足條件；

(6)將解碼后的最佳懲罰參數和核函數參數用來建立支持向量回歸模型；

(7)利用該模型進行壽命預測。

2.6 機械密封壽命預測方法

針對傳統聲發射參數分析方法準確度較低、易受環境影響，模型預測準確度不高的問題，對機械密封聲發射信號進行了如下處理：首先對數據進行小波降噪處理，再對降噪信號進行小波包分解，對各頻帶的子信號進行特征抽取，得到大量聲發射特征，再利用KPCA對特征矩陣降維處理，得到貢獻率高的少量特征，再利用馬氏距離進行特征融合，最后利用QPSO算法優化SVR支持向量回歸進行壽命預測。

3 聲發射信號處理

3.1 信號的特征提取

由于有環境噪聲的產生，從實驗采集的樣本可以看出低頻部分有很多毛刺。為削弱背景噪聲的影響，突出有用信號，對樣本數據采用小波降噪，濾掉了低頻噪聲信號，保留了高頻有用信號，降噪效果非常明顯，如圖4所示。

圖4 降噪前后聲發射信號對比

由于表征聲發射信號特征眾多，以及缺乏明確的退化指標，故采用特征融合的方式建立所需的退化指標。首先對每個頻帶的子信號提取表1中的特征，共計得到120個特征。然后將得到的高維特征進行降維處理，通過核主成分分析(KPCA)把貢獻率大于90%的特征提取出來，特征如圖5所示。

圖5 KPCA優化特征

為了得到唯一的退化指標，利用馬氏距離對KPCA后的特征進行融合。經過磨合期和平穩期后機械密封性能急劇退化，該過程隨時間變化，如圖6所示。

圖6 融合后的馬氏距離

對剩余3組全壽命數據采用同樣的信號處理方法，得到相應的退化指標。

3.2 壽命預測

將退化指標分為訓練樣本集1、2、3和測試樣本集4。利用訓練樣本集對量子行為粒子群算法優化支持向量回歸機(QPSO-SVR)進行訓練，再利用測試樣本集對該模型的預測能力和有效性進行校驗。其中設置QPSO-SVR的種群數量為30，迭代次數為300，選擇RBF核作為SVR的核函數，確定懲罰參數c和核函數參數的取值范圍均為[0,100]。通過樣本集的訓練，得到最終的懲罰參數c為0.324，核函數參數g為0.841。

經過計算，得到如表2所示預測模型對訓練數據的預測誤差。表中數據表明，預測誤差較小，預測結果較好。將預測樣本集輸入QPSO-SVR模型，得到表2所示結果，證明了該模型有著較高的準確度。

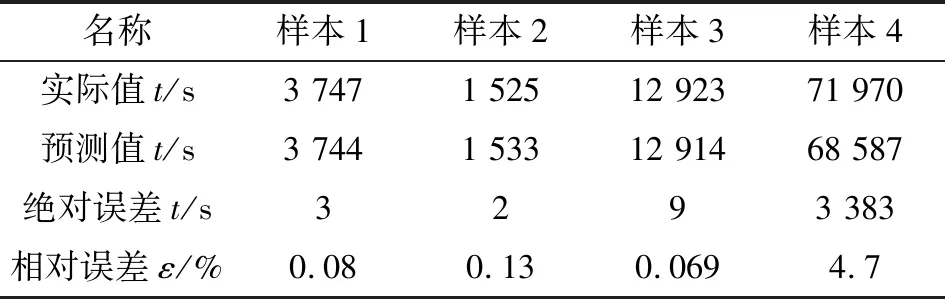
表2 QPSO-SVR模型預測結果

為了進一步說明QPSO-SVR模型在參數優化和預測準確度方面的效果，建立普通的SVR模型進行壽命預測。人為設定懲罰參數c為1，核函數參數g為1.2，采用上述預測過程，同樣訓練樣本為1、2、3，測試樣本為4。QPSO-SVR和SVR預測曲線如圖7所示，絕對誤差對比圖如圖8所示，結果如表3所示。經過QPSO改進后的SVR預測模型比普通的SVR預測模型更加接近真實的壽命退化過程，預測準確度高于普通的SVR預測模型。

圖7 QPSO-SVR與SVR估計剩余壽命以及真實壽命對比

圖8 QPSO-SVR與SVR估計剩余壽命的絕對誤差對比

表3 QPSO-SVR和SVR模型預測結果

Table 3 Prediction results of QPSO-SVR model and SVR model

名稱SVRQPSO-SVR懲罰參數10.324核函數參數1.20.841相對誤差11.84%4.7%

為了證明QPSO-SVR模型在有著良好的泛化能力，在原聲發射信號的基礎上加入高斯白噪聲，用訓練好的QPSO-SVR模型和SVR模型進行壽命預測。QPSO-SVR和SVR預測曲線如圖9所示，絕對誤差對比圖如圖10所示，結果如表4所示。經過QPSO改進后的SVR預測模型比普通的SVR預測模型具有更高的精度。通過原信號和加噪信號兩組不同信號的預測結果對比，說明了QPSO-SVR模型不僅有著更高的精度，同時有著良好的泛化能力。

圖9 加入高斯噪聲后QPSO-SVR與SVR估計剩余壽命以及真實壽命對比

圖10 加入高斯噪后QPSO-SVR與SVR估計剩余壽命的絕對誤差對比

表4加噪聲后QPSO-SVR和SVR模型預測結果

Table 4 Prediction results of QPSO-SVR model and SVR model after adding Gauss noise

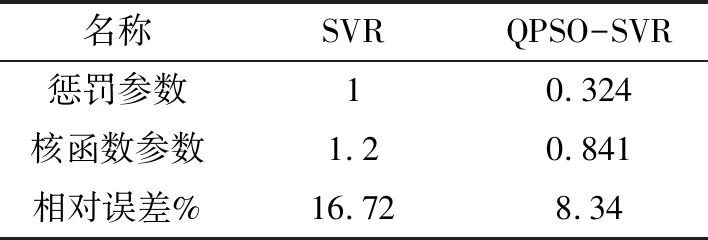
名稱SVRQPSO-SVR懲罰參數10.324核函數參數1.20.841相對誤差%16.728.34

4 結論

(1)采用多種統計特征，結合特征之間的優缺點，利用KPCA進行特征優化，得到主要的特征成分。通過馬氏距離融合出退化指標，表征機械密封性能退化過程，簡化了模型訓練的輸入參數。

(2)對比普通SVR模型和QPSO-SVR模型的效果，結果表明，QPSO-SVR避免了參數設定的盲目性，應用QPSO方法尋找到全局最優的參數值，模型有著較好的泛化能力和預測準確度，得到了較好的回歸模型，對金剛石涂層機械密封壽命預測具有一定意義。