基于一方程轉捩模型的狹縫沖擊射流傳熱數值模擬

黃華坤 ，張桂勇*，2，3，孫鐵志 ，宗智 ，2，3

1大連理工大學船舶工程學院遼寧省深海浮動結構工程實驗室，遼寧大連 116024

2大連理工大學工業裝備結構分析國家重點實驗室，遼寧大連 116024

3高新船舶與深海開發裝備協同創新中心，上海200240

0 引 言

沖擊射流現象是指具有一定速度的流體通過撞擊物體表面，使得撞擊區形成極薄的邊界層，從而得到較高傳熱效率的現象。沖擊射流傳熱原理被廣泛應用于工業生產，如紙張干燥和電子元器件冷卻等。在船舶領域，船舶甲板上的武器發射、無人機發射和垂直起降飛機起飛過程中產生的高溫高速噴射氣流，不僅會引起甲板的燒蝕，而且還會帶來殘余熱應力的影響。因此，準確預測沖擊射流的物理現象，對其工業應用具有重要意義。

許多學者對沖擊射流現象開展了研究。Gardon等［1］通過實驗發現，在較低沖擊距離下，以局部努塞爾數（Nu）表示的傳熱率表現出第2峰值的特征；當沖擊距離較大時，局部努塞爾數的第2峰值消失。Colucci等［2］研究了低沖擊距離下（H/D ＜2，H/D為圓形沖擊射流的沖擊距離，H為沖擊高度，D為噴嘴直徑）的沖擊射流現象，指出局部努塞爾數第1峰值主要受邊界層厚度的影響，第2峰值主要受層流到湍流轉捩的影響。隨著計算流體力學（CFD）和計算機技術的發展，CFD方法被廣泛用于模擬沖擊射流現象。在早期的數值研究中發現，兩方程湍流模型在滯止點處易產生較高的湍動能 k［3-4］，為此，Kato-Launder模型被用于降低滯止點處的湍動能［5］。此外，針對局部努塞爾數第2峰值的特征，研究表明，SST k-ω模型表現較好［6］。然而，Dutta等［7］指出，基于SST k-ω的低雷諾數模型雖然在低沖擊距離下（H/B=4，H/B為狹縫沖擊射流的沖擊距離，B為噴嘴寬度）獲得了第2峰值的特征，但在沖擊距離變大時（H/B=9.2），該模型預測出了實際不存在的第2峰值。為正確反映沖擊射流在不同高度下的特點，Alimohammadi等［8］研究了基于轉捩理論的四方程γ-θ模型（也稱Transition SST模型）在圓形沖擊射流中的表現。結果表明，γ-θ模型可準確預測圓形沖擊射流的傳熱特征；針對不同的沖擊高度，γ-θ模型表現出較好的預測能力。但在圓形沖擊射流中表現良好的湍流模型在狹縫沖擊射流中可能獲得較差的結果，反之亦然［9］。同時，γ-θ模型不能預測滯止區附近低湍流強度（Tu＜0.5%）下的橫流失穩現象。

因此，本文擬引入基于γ-θ模型的一方程轉捩模型來模擬狹縫沖擊射流現象。該模型耦合了橫流轉捩模型，在模擬橫流失穩現象和分離流問題上具有一定的優勢。同時，將一方程轉捩模型與Kato-Launder模型和SST k-ω模型耦合，并在此基礎上研究一方程轉捩模型在預測狹縫沖擊射流傳熱規律上的表現。

1 數值計算方法

1.1 控制方程

不可壓縮湍流流動的時均Navier-Stokes方程的質量守恒方程、動量方程和能量方程分別為：

式中：ρ為密度；μ為動力粘性；u和u′分別為平均速度和脈動速度；p為壓力；Cp為比熱容；K為傳熱率；T和T′分別為平均溫度和脈動溫度；分別為雷諾應力張量和湍流熱通量矢量；i和j分別為x，y方向。

1.2 SST k-ω湍流模型

本文采用Menter［10］提出的一種混合標準k-ε模型和k-ω模型的SSTk-ω模型。該模型的湍流粘性系數μt定義為

式中：k為湍動能；ω為比耗散率；α*為阻尼因子；a1=0.31；S為應變率；，y為到壁面的距離。

為了封閉控制方程，在模型中增加了湍動能k和比耗散率ω方程，表達式為：

式中，Gk為湍動能k的產生項；Gω為比耗散率ω的產生項；Yk，Yω分別為k和ω的耗散；Dω為交叉擴散項；Sk，Sω分別為k和ω的源項；σk和σω通過混合函數F1進行定義，具體為

式中，下標1，2分別為k-ω模型和k-ε模型的湍流常數。

1.3 Kato-Launder模型

Kato-Launder模型修正在Gk中采用渦量代替某個應變率，能避免兩方程模型在滯止點處預測的湍動能k過高的問題。由于在滯止點附近的流動幾乎呈無旋狀態，渦量趨于0，因此湍動能k變小。該方程的湍動能產生項為

Kato和Launder修正后的表達式為

1.4 一方程轉捩模型

在γ-θ模型中引入了轉捩臨界動量厚度雷諾數和間歇因子輸運方程。基于γ-θ模型的一方程轉捩模型保留了間歇因子輸運方程，同時使用經驗關系式取代了臨界動量厚度雷諾數方程。其中間歇因子γ的輸運方程為

式中：σγ=1.0；Pγ和Eγ的定義為

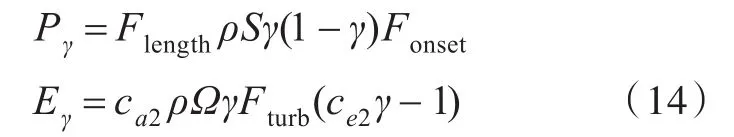
式中：Flength為控制轉捩區的長度；ca2=0.03，ce2=50；Fonset和Fturb的定義為

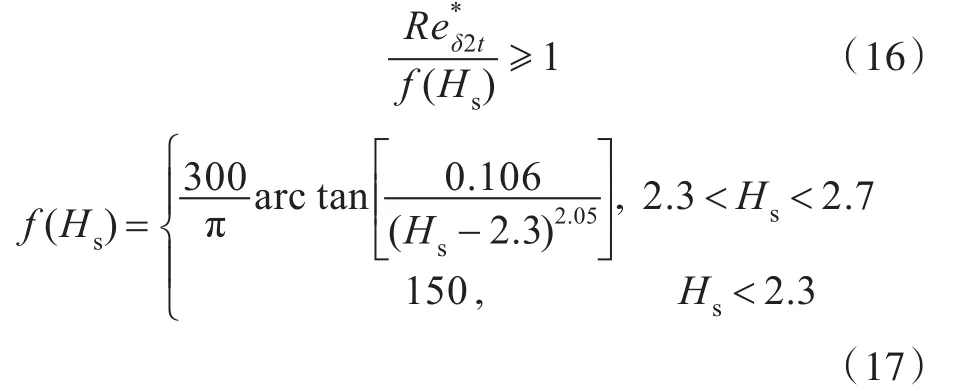
1.5 計算模型及求解設置

計算模型如圖1所示，L為沖擊板長度。由于計算模型關于y軸對稱，為提高計算效率，建立1/2模型進行計算。表1給出了計算模型尺度和網格節點分布情況。

圖1 沖擊射流的計算模型Fig.1 The computational model for jet impingement flow

本次計算基于Fluent軟件，使用有限體積法對計算域進行離散，選擇壓力基穩態求解器和壓力耦合方程半隱式（SIMPLE）算法。梯度離散格式采用最小二乘法，壓力離散格式采用交錯壓力格式（Pressure Staggering Option），其他離散格式采用二階迎風格式。湍流模型采用SST k-ω模型、Kato-Launder模型和轉捩模型（以下簡稱為“一方程轉捩模型”）。網格劃分方案如圖1所示。本文采用結構型網格，根據 Jaramillo［12］的研究，保持第1層網格節點與壁面間的無量綱距離y+＜2.5（，其中τw為壁面處的切應力），如圖2所示。在壁面和射流出口附近進行網格加密，加密方向如圖1箭頭方向所示，以漸疏式網格擴展到整個計算域，同時保證網格膨脹率小于2。表1給出了計算模型尺度以及進行網格無關性檢驗后在x軸和y軸方向的節點分布情況。

2 結果分析與討論

2.1 穩態沖擊射流驗證

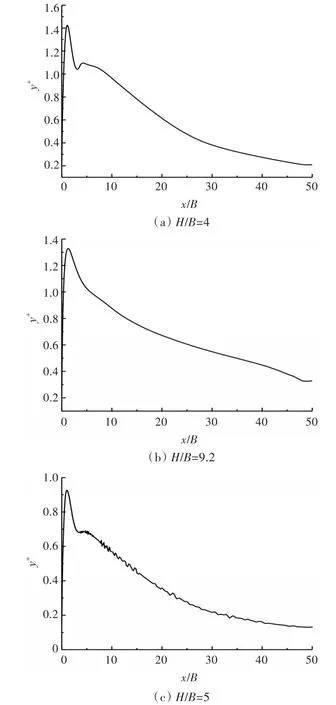
圖2 3種算例下 y+沿沖擊板的分布Fig.2 y+distributions along the impinging plate for 3 cases

表1 計算模型的尺度和網格節點分布Table 1 Scale and nodes distribution of computationalmodel

為了驗證一方程轉捩模型對穩態沖擊射流換熱的有效性，本文采用了 Ashforth-Frost等［13］的實驗工況，并與其他學者的數值計算結果進行了對比。實驗研究結果表明，在H/B=4時，局部努塞爾數表現出明顯的第2峰值特征；而在H/B=9.2時，局部努塞爾數的第2峰值消失。這2個算例可以驗證一方程轉捩模型對轉捩的預測能力。Ashforth-Frost等［13］的實驗是在1個標準大氣壓下進行的。射流出口溫度為恒溫300 K，射流出口平均速度雷諾數基于射流出口寬度，其大小為20 000。沖擊板設為恒溫310 K，無滑移固定壁面。上限板設為恒溫300 K，無滑移固定壁面。出口采用出流（outflow）邊界條件，出口壓力為1個大氣壓P=101 325 Pa。計算的普朗特數Pr=0.72。

圖3給出了H/B=4時，得到的局部努塞爾數與實驗數據以及其他學者的數值結果沿沖擊面的分布情況。從圖中可以看出，一方程轉捩模型可準確預測局部努塞爾數第1峰值和第2峰值的大小及位置。受轉捩過程影響，在3≤x/B≤7范圍內，傳熱率逐漸升高；當轉捩完成后，傳熱率逐漸降低。在滯止點附近，流動處于低湍流強度狀態，即準層流狀態，這使得滯止點附近相對于壁面射流區的傳熱率得到了極的大提高。

圖3 H/B=4時局部努塞爾數分布Fig.3 The distribution of local Nusselt number（H/B=4）

受益于Kato-Launder模型修正作用，可用一方程轉捩模型準確預測局部努塞爾數的第1峰值。如前所述，在滯止點處，流動幾乎處于無旋狀態，因此Kato-Launder模型中渦量的引入使滯止點處的湍動能下降；且在第2峰值附近可明顯看到渦的存在（圖4）。雖然Kato-Launder模型無法對渦進行計算，但是渦的脫落導致渦量增加，故一方程轉捩模型在2次峰值附近預測的傳熱率與SST k-ω模型相比有所增加，從而提高了渦附近湍動能的預測精度［14］。而無修正模型的RANS k-ω模型［15］和 SST k-ω模型在滯止點處過高地預測了局部努塞爾數。其中RANS k-ω模型無法預測局部努塞爾數的第2峰值。SST k-ω模型雖然能夠預測第2峰值，但其預測結果低于實驗值，且第2峰值的位置與實驗值相比提前了31%，這也說明轉捩模型的加入使一方程轉捩模型具備了良好的轉捩預測能力。因粘性底層的流動狀態與湍流轉捩相關，故沒有粘性底層修正的SST k-ω模型和RANS k-ω模型難以準確預測轉捩區間的位置。RANS/LES模型［15］繼承了大渦模擬（LES）模型在滯止點附近湍流強度幾乎為零的特點，因此正確地捕捉到了局部努塞爾數的第1峰值，但卻提前預測了第2峰值的位置。除一方程轉捩模型外，其他數值模型同樣存在第2峰值預測不準確的現象。整體上，一方程轉捩模型獲得了與實驗結果基本一致的分布趨勢，這說明該模型不僅能準確模擬滯止點附近的流動狀態，還能準確預測壁面射流區層流到湍流的轉捩過程。

圖4 H/B=4時的流線圖Fig.4 The streamlines for H/B=4

圖5給出了H/B=9.2時的數值計算與實驗結果中局部努塞爾數沿沖擊面分布的對比結果。從圖可看出，局部努塞爾數的第2峰值消失。圖6顯示了H/B=9.2時的流線圖，可見回流中心位置較H/B=4時的遠，因此在0≤x/B≤10范圍內受渦的影響較小。由于轉捩受渦的影響，其對傳熱的影響變弱，局部努塞爾數的第2峰值消失。RANS/LES模型和一方程轉捩模型的預測結果與實驗結果吻合較好。此外，RANS k-ω模型［15］在滯止點附近預測的局部努塞爾數與實驗值相比更低。這是因為在較大的沖擊距離下，模型中的應力限制器對流動幾乎無影響，這導致滯止點附近的湍流強度升高，傳熱率下降。而RANS/LES模型［15］則稍好于RANS k-ω模型［14］，但誤差仍然有12%。一方程轉捩模型較為準確地預測了滯止點處的局部努塞爾數。RANS k-ω模型［14］預測的局部努塞爾數第2峰值與實驗值不相符，而RANS/LES模型和一方程轉捩模型在趨勢上則與實驗結果基本保持一致。與一方程轉捩模型相比，SST k-ω模型在滯止點處過高地預測了局部努塞爾數，這反映出Kato-Launder模型起到了降低滯止點處湍動能的作用。但在下游區域，SST k-ω模型與一方程轉捩模型預測的局部努塞爾數基本一致，這說明在高沖擊射流情況下，轉捩模型對傳熱預測的影響較小，同時表明一方程轉捩模型可正確反映沖擊射流中的轉捩強度，從而準確給出局部努塞爾數的分布。

圖5 H/B=9.2時局部努塞爾數分布Fig.5 The distribution of local Nusselt number（H/B=9.2）

圖6 H/B=9.2時的流線圖Fig.6 The streamlines for H/B=9.2

2.2 脈動沖擊射流驗證

脈動沖擊射流與穩態沖擊射流的不同之處在于，其提供了一個擾動源。Lytle等［16］的研究表明，平行于沖擊面的速度脈動峰值與沖擊面的平均傳熱率峰值相關，而擾動源又與渦的形成相關。渦影響了射流的發展以及層流到湍流的轉捩過程，進而影響到沖擊面上的傳熱分布。在此，我們采用了Mladin等［17］的實驗工況。在本算例中，射流出口采用正弦變化的速度分布，其公式為

式中：vavg為入口的平均速度；A為脈動幅度；fr為脈動頻率；t為時間。射流進口溫度為300 K。沖擊板是厚度為5 mm的鋁鎳材質，導熱率為150 W·m-1·K-1，溫度設為 323 K，無滑移固定壁面；上限板的溫度設為恒溫300 K，無滑移固定壁面。出口設置為出流邊界條件，出口壓力為1個大氣壓P=101 325 Pa。計算得到的沖擊高度為H/B=5，普朗特數Pr=0.72。

圖7給出了在穩定狀態下局部努塞爾數沿沖擊面的分布情況。從圖中可以看出，局部努塞爾數的第2峰值仍然較為明顯。這是因為回流中心在x/B=10.8處，如圖8所示。一方程轉捩模型能準確捕捉到滯止點處局部努塞爾數的大小，同時也能準確預測局部努塞爾數第1個最低點的值。而k-ω-v2-f（k-ω模型和v2-f模型）混合模型［18］則過低地預測了滯止點和最低點處的局部努塞爾數；在下游區，k-ω-v2-f模型［18］的表現較一方程轉捩模型差。一方程轉捩模型獲得了與實驗基本一致的結果。這是因為一方程轉捩模型引入了間歇因子輸運方程來模擬轉捩，而轉捩的發生與擾動相關，因此對于脈動沖擊射流，一方程轉捩模型依然能夠給出較為準確的結果。

3 結 語

本文提出采用一方程轉捩模型對狹縫沖擊射流問題進行數值模擬，并研究不同沖擊高度、不同雷諾數下的穩態沖擊射流和脈動沖擊射流傳熱分布規律。結果表明，一方程轉捩模型不僅能捕捉到局部努塞爾數的第1峰值，也能準確預測受轉捩影響的局部努塞爾數第2峰值的大小和位置。在4≤H/B≤9.2時，一方程轉捩模型在傳熱預測上表現出了良好的魯棒性特征。