基于彎矩影響系數的軸系安裝狀態評估逆計算方法

陳昊，周瑞平*，雷俊松，張建軍

1武漢理工大學能源與動力工程學院，湖北武漢430063

2中國船級社上海規范研究所，上海200135

0 引 言

船舶推進軸系安裝狀態的好壞直接影響到軸系長期運行的可靠性，必須在其安裝完成后進行檢驗，確定軸系的狀態。應變檢測是一種精度高且適用性強的檢測方法，已成為船舶軸系安裝檢測的主要方法之一。針對船舶推進的應變測試技術發展至今已有30余年，其測試方法和分析模型也有很多種。Cowper等［1］利用應變測量和力矩平衡原理，在集裝箱船和車輛滾裝船上進行了實船測試及軸承負荷分析。汪驥等［2］研究了基于應變波形和力矩平衡原理的軸承負荷檢測方法，這兩者都是以力矩平衡原理直接計算出艉軸承和中間軸承的軸承負荷，無法計算主機負荷和其他狀態參數。Zhang等［3］提出了一種結合傳遞矩陣法和應變檢測對渦輪機組軸系狀態進行分析的方法，其測量對象為渦輪機組，相對船舶推進軸系其測點布置限制較少。美國船級社（ABS）［4］結合應變測量與遺傳算法開發了軸承變位測量軟件，并將其應用于船體變形研究。日本船級社（NK）［5］在其軸系校中指南中介紹了彎矩影響數以及如何將其用于軸承變位求解的方法，但沒有對不同類型軸系的測點布置規律和布點優化進行系統研究。

目前，軸系校中計算的理論方法主要有傳遞矩陣法、三彎矩法和有限元法。其中，傳遞矩陣法在截面數過多時易產生較大的累積誤差；三彎矩法計算精度較高，相比有限元法具有編程容易的特點［6］。三彎矩法雖然求解計算量大，但其將軸系整體受力情況歸納到了一個矩陣方程中，便于分析軸系各部分之間的相互影響。

本文將從三彎矩方程入手，推導彎矩影響系數，借助軸系任意截面彎矩與軸承變位的線性關系，列線性方程來推算軸系狀態。首先，對彎矩影響系數的特性進行研究，推導不同軸系以直接求解最大軸承數，并在此基礎上得出適用于不同軸系類型的測點布置規律。然后，對不同測點布置下求解矩陣的條件數進行分析，得出測點優化布置的原則。最后，根據38 500 DWT散貨船實軸測試數據推算其軸系狀態，驗證計算方法的正確性，為軸系應變測試提供一種新的思路。

1 彎矩影響系數法

1.1 彎矩影響系數的推導

對于具有n個截面的變截面梁軸系模型，一共可以列出n-2個三彎矩方程［7］：

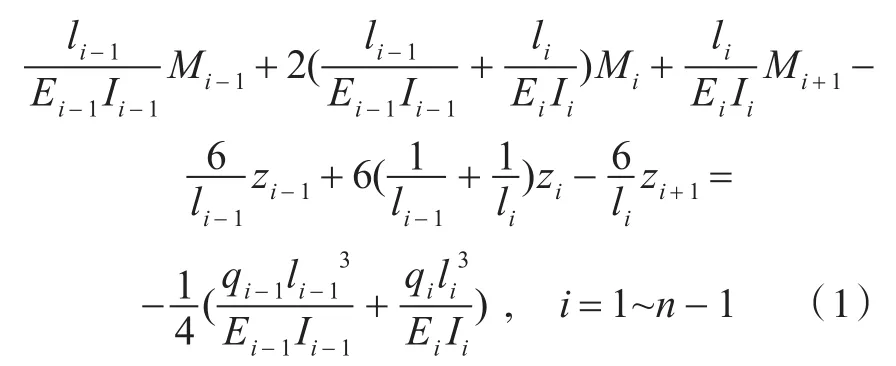
式中，li為軸系各單元的長度；EiIi為彎曲剛度；qi為均布載荷；Mi為各截面的彎矩；zi為各截面的撓度。再加上首、尾截面2個邊界條件方程以及n個虛支承處支反力為0或實支承處撓度為軸承變位的補充方程，共計2n個方程，可以解出n個截面彎矩和n個截面撓度，將其表示成矩陣形式：

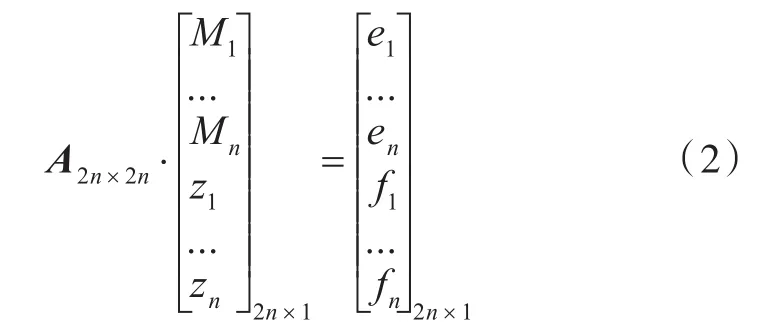
式中，A為2n×2n的系數矩陣；向量C=［e1…en f1…fn］T中各項由方程右側常數確定，對于建立完成的模型，這兩者是定常的；向量X=［M1…Mnz1…zn］T為一個2n行的列向量，表示所要求解的彎矩與撓度。式（2）又可以表示為A-1·C=X，包含2n個方程，前n個用于求解彎矩的方程可以表示為

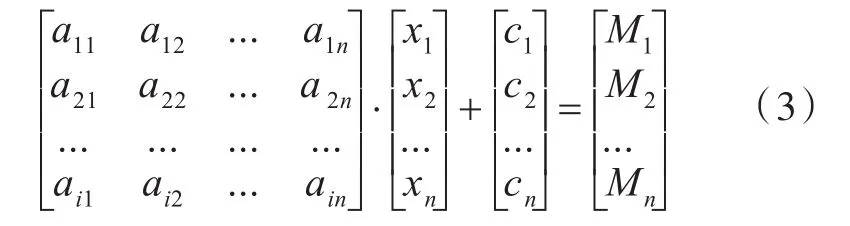
式中：xi為第i個軸承的變位；ci為直線狀態下該截面處的彎矩值；ain為第n個軸承單位變位對第i個截面所造成的彎矩變化量，即彎矩影響系數，kN。對于含有n個軸承和m個截面的軸系來說，其彎矩影響系數可以組成一個m×n的矩陣，每一列都為一個軸承對所有截面的彎矩影響系數。

1.2 基于彎矩影響系數的軸系狀態逆計算方法

在推導出彎矩影響系數后，利用軸承變位與截面彎矩之間的線性關系，列出線性方程可以求解軸承變位，進而得出軸系整體狀態：

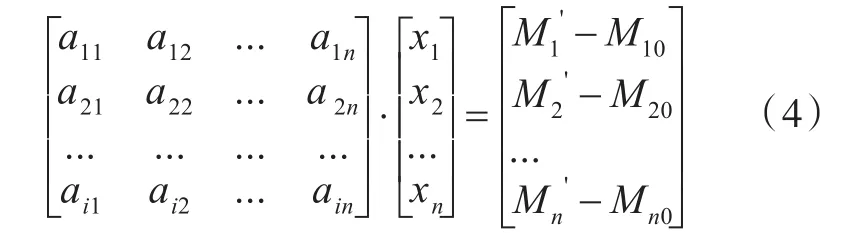
式中，xn為第n個軸承的實際變位；為第n個軸承的實際彎矩；Mn0為第n個軸承在直線狀態下的彎矩。理想情況下，若要求得n個軸承的變位，只需測得n個截面處的彎矩即可。需要注意的是，為得出正確的計算結果，必須盡可能正確簡化模型來得到正確的直線彎矩值。

2 測點布置規律與優化原則

2.1 彎矩影響系數性質

研究發現，式（4）中的系數矩陣是不滿秩的，原因是矩陣各行線性相關，造成矩陣奇異。要找出矩陣奇異的原因，必須對彎矩影響系數的性質進行研究。圖1為4#軸承彎矩影響系數在軸線方向上的分布。

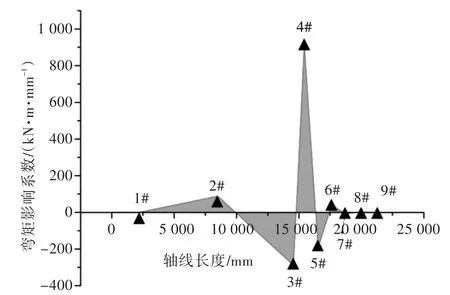
圖1 軸承彎矩影響系數分布圖Fig.1 Distribution of bending moment influence coefficient on shaft

從圖1可以看出：每個軸承的彎矩影響系數在軸線長度方向上都為連續直線，且在每一跨梁內斜率、截距均各不相同；越靠近軸承的截面其彎矩影響系數越大，越遠離軸承的截面其彎矩影響系數越小；從船艉向船艏看，在第1個軸承前（包括第1個軸承處）及最后一個軸承后（包括最后一個軸承處），彎矩影響系數均為0。

對含有n個軸承的軸系，由于彎矩影響系數與截面位置成線性關系，第1跨梁和第n-1跨梁內獨立彎矩數最大為1，第2至第n-1跨梁內獨立彎矩數最大為2，當跨梁內待測彎矩數大于最大獨立彎矩數時，可以依據線性關系確定跨梁中所有截面的彎矩。前一跨梁內所有截面彎矩確定后，后一跨梁會減少1個獨立彎矩數。

將1～n-1跨梁內所有獨立彎矩數相加，可以發現整個軸系最多只存在n-2個獨立彎矩，這就造成了彎矩影響系數矩陣的秩最大為n-2，即使軸系上布置超過n-2個測點，最多也只存在n-2個獨立方程，若測點布置不合理，比如將所有測點布置在同一跨梁內，獨立方程數會低于n-2。

為求解出全部軸承的變位，需對軸系進行處理。若所有跨梁都可以布置測點，選擇任意n-2個跨梁各布置一處彎矩測點，并將首個軸承和末軸承的變位設為0，這相當于對軸系整體作剛性約束。整個軸系的變位可以表示為［0 x1x2…xn-10］，而軸系實際可能是在此基礎上旋轉一定角度。這樣的旋轉不會改變軸承間相對位置，對于軸系校中計算不會產生影響。

與渦輪機等軸系不同的是，船舶推進軸系受現場條件的限制，有部分跨梁，如艉軸管內和主機內部無法布置測點，這樣會導致獨立彎矩數進一步減少。因此，需要針對這類軸系作出假設。圖2與圖3分別為單艉軸承和雙艉軸承軸系彎矩影響系數的分布情況。

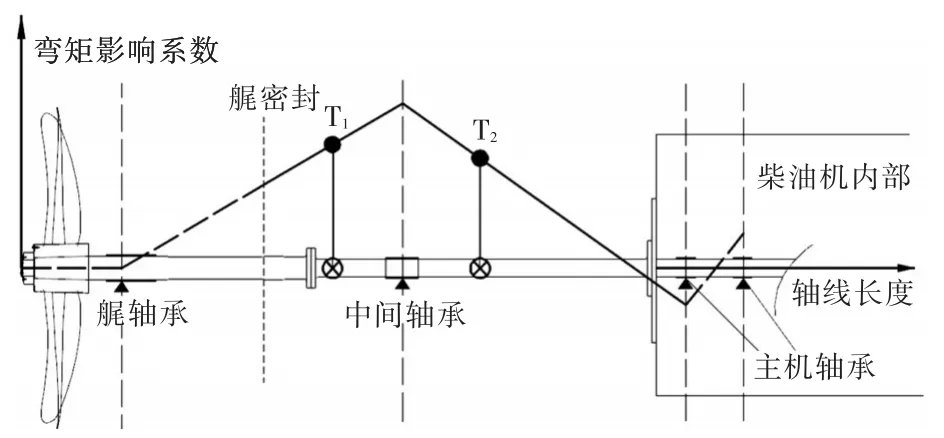
圖2 單艉軸承彎矩影響系數圖Fig.2 Bending moment influence coefficient for single stern tube bearing shaft

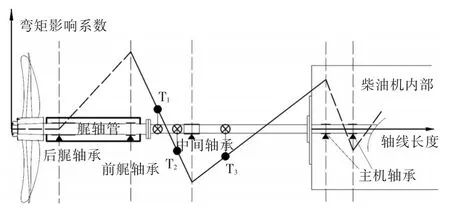
圖3 雙艉軸承軸系彎矩影響系數圖Fig.3 Bending moment influence coefficient for double stern tube bearing shaft

由圖2與圖3可以看到，對于單艉軸承和雙艉軸承軸系，由于測點布置位置受限，軸上獨立彎矩數分別為NIB+1與NIB+2，其中，NIB為中間軸承數。為求出所有軸承的變位，對軸系進行如下假設：

1）艉軸管及船艉結構剛度很大，將艉軸管軸承的變位均設為0或已知量。

2）主機內軸段無法布置測點，但考慮到主機軸承一般是整體安裝，對于單艉軸承軸系，以彎矩影響系數方程計算中間軸承和1號主機軸承變位，假設其余主機軸承變位與1號主機軸承相同或所有主機軸承按已知傾斜角位于同一直線上；對于雙艉軸承軸系，以彎矩影響系數方程計算中間軸承和第1，2號主機軸承變位，假設其余主機軸承與1，2號主機軸承位于同一條直線上。在這樣的假設下，通過給定艉軸承高度并補充主機軸承約束，可以通過式（5）和式（6）分別對單艉軸承和雙艉軸承進行軸承變位求解。

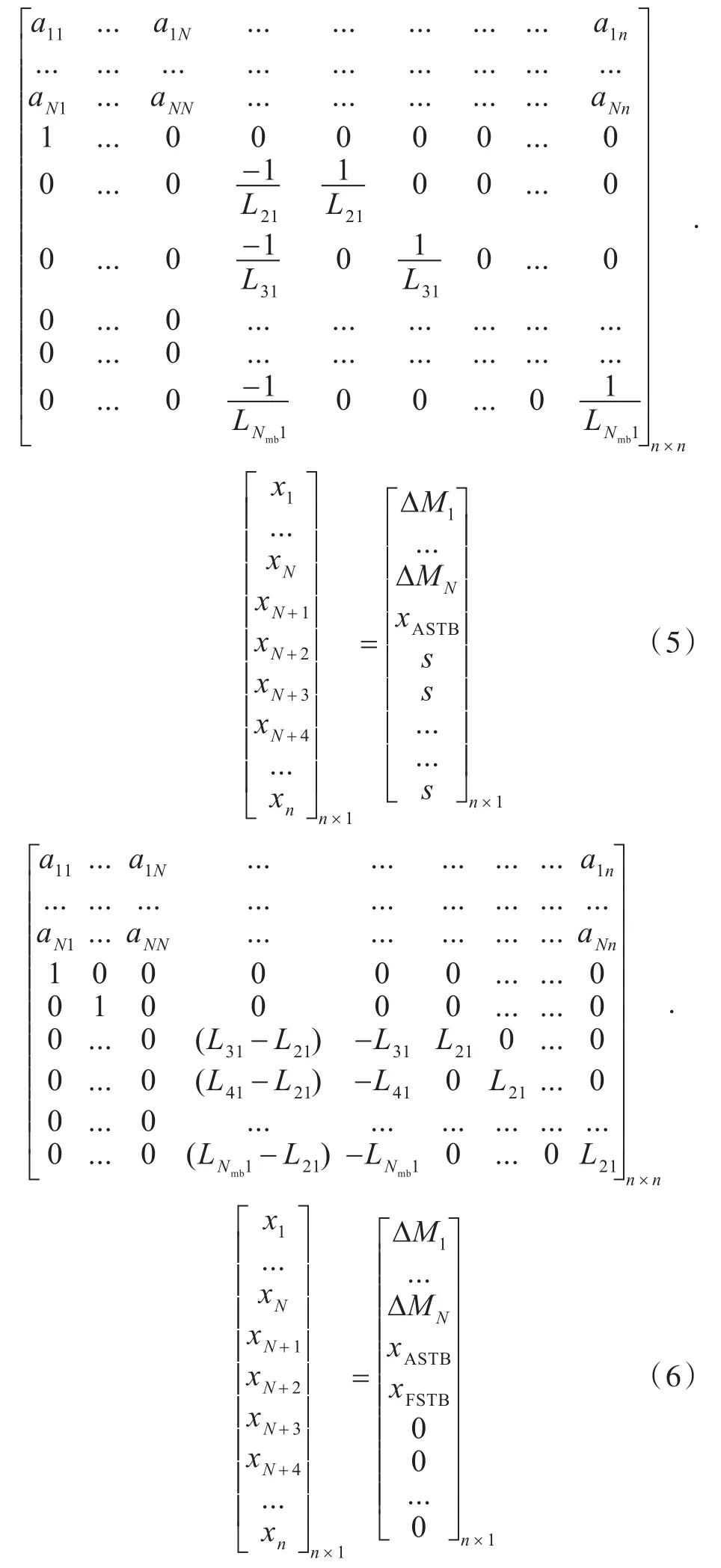
式中：對于單艉軸承模型，N為NIB+1，對于雙艉軸承模型，N為NIB+2；Ln1為第n個主機軸承與第1個主機軸承間的距離；Nmb為主機軸承數；xASTB與xFSTB分別為后艉和前艉軸承給定高度；s為單艉軸承模型中給定的主機軸承傾角，若主機水平安裝，則s=0。

2.2 測點優化布置原則

實測中，因操作或者儀器本身的精度問題，測得的彎矩會有一定的誤差。將測點布置在跨梁內不同的位置得出的不同求解矩陣對誤差的敏感度不同，反映在實際的測試中表現為，即使所有測點的彎矩絕對測量誤差都很小，計算出的軸承變位也可能與真實值有很大偏差。因此，在布置測點時，應該選擇合理的位置。

為找出可能引起求解矩陣誤差敏感度上升的位置，針對圖4所示的測點布置方案，研究了誤差敏感度與T1～T4這4個測點在各自跨梁內位置的關系，得到圖5。其中圖5（a）表示誤差敏感度隨T2，T3測點在同一跨梁內位置變化的情況，圖5（b）表示誤差敏感度隨T1，T4測點在各自跨梁內位置變化的情況。圖中誤差敏感度是用求解矩陣的條件數表征的，條件數越大，表示矩陣的誤差敏感度越大。為便于研究，每次只有2個測點的位置發生改變，其他測點位置保持不變。

圖4 測點布置圖Fig.4 Arrangement of strain test points

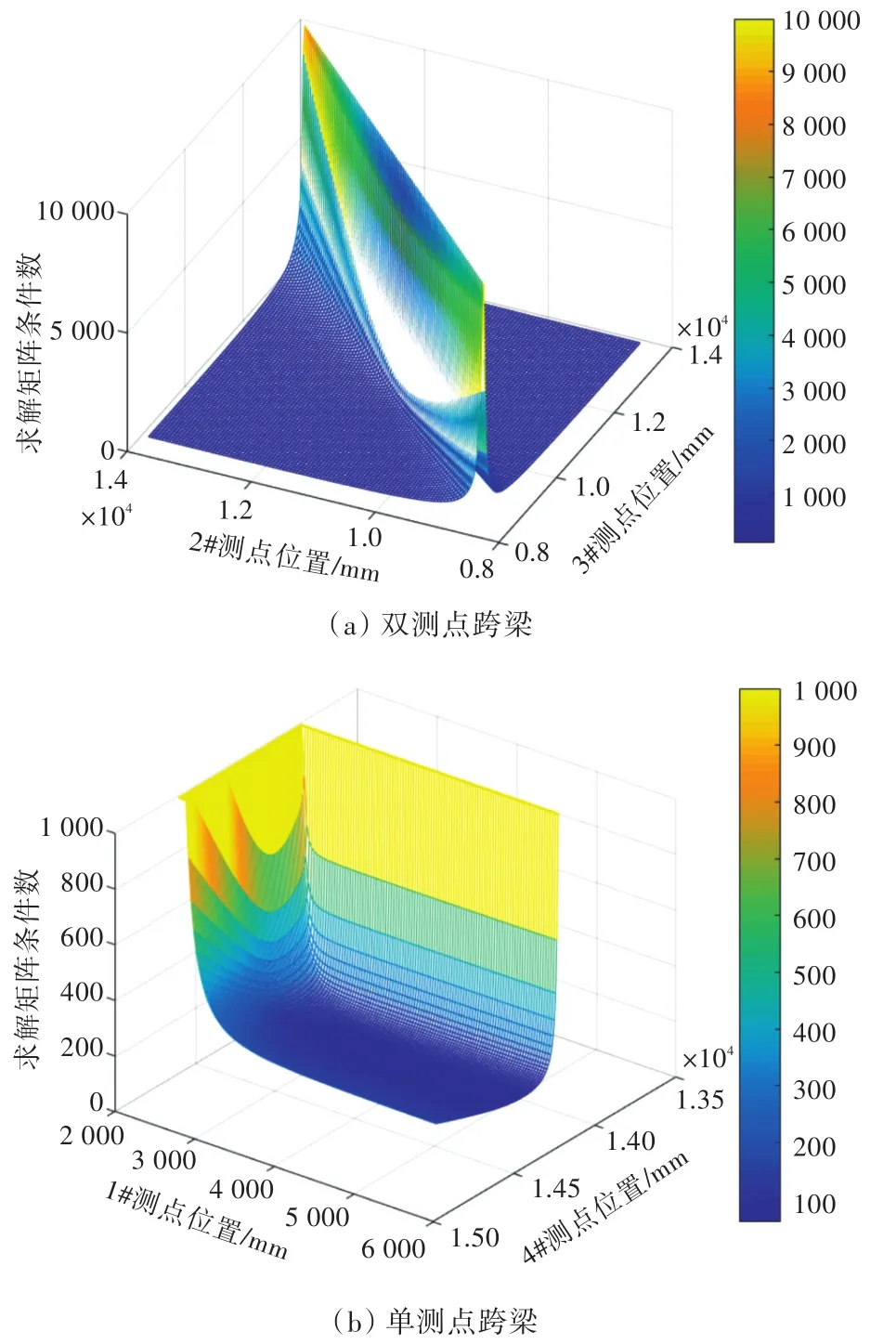
圖5 誤差敏感度圖Fig.5 Plot of error sensitivity

由圖5（a）可以看出，若同一跨梁內布置有2個測點，則2個測點的位置相距越近，矩陣條件數越大；當2個測點接近重合時，條件數趨于無窮大。因此，在同一跨梁內布置2處測點時，應增大這2個測點間的距離。

由圖5（b）可以看出，T1測點靠近1#軸承時以及T4測點靠近4#軸承時，矩陣條件數都會急劇上升，當測點位置與軸承位置接近重合時，矩陣條件數會趨于無窮大。這是因為當測點位置與軸承重合時，總的獨立彎矩數會減1，造成矩陣奇異。因此，若測點位置與軸承重合后獨立彎矩數減少，應增大測點與該軸承的距離。

在實際測量中，為提高計算準確度，可以采集超過所需測點數的截面彎矩，通過最小二乘算法（LMS）進行計算，但仍須保證有效測點數不少于該模型需要的獨立方程數。

圖6是利用彎矩影響系數計算船舶推進軸系安裝狀態的逆計算流程。

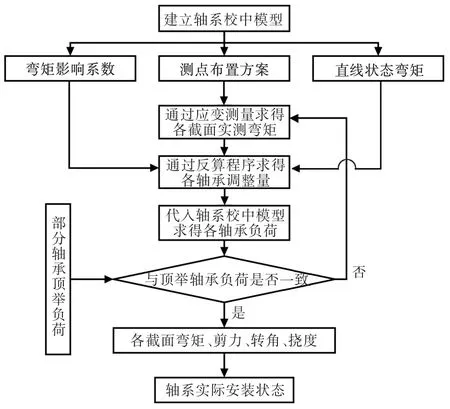
圖6 彎矩影響系數法軸系安裝狀態檢驗流程圖Fig.6 Flow diagram of bending moment influence coefficient method

3 實船驗證

根據上文提到的軸系狀態逆計算方法，對某38 500 DWT散貨船軸系進行了彎曲應變測量，并根據測量結果對軸系狀態予以了反推。

3.1 彎矩測量原理

在軸上測點位置粘貼應變片，通過采集軸旋轉一周內應變信號的變化，得出軸上對應位置的彎曲應變值，進而得出該位置的彎矩值。具體原理如圖7所示。

如圖7（a）所示，應變片從水平位置開始隨軸旋轉，由于軸表面的彎曲應變ε與其距彎曲中性面的距離r成正比。因此，軸旋轉一周彎曲應變的波形如圖7（b）所示，在不考慮橫向彎曲的情況下，該截面處的最大彎曲應變εi為波形最高點與最低點差值的一半［8］，如式（7）所示。

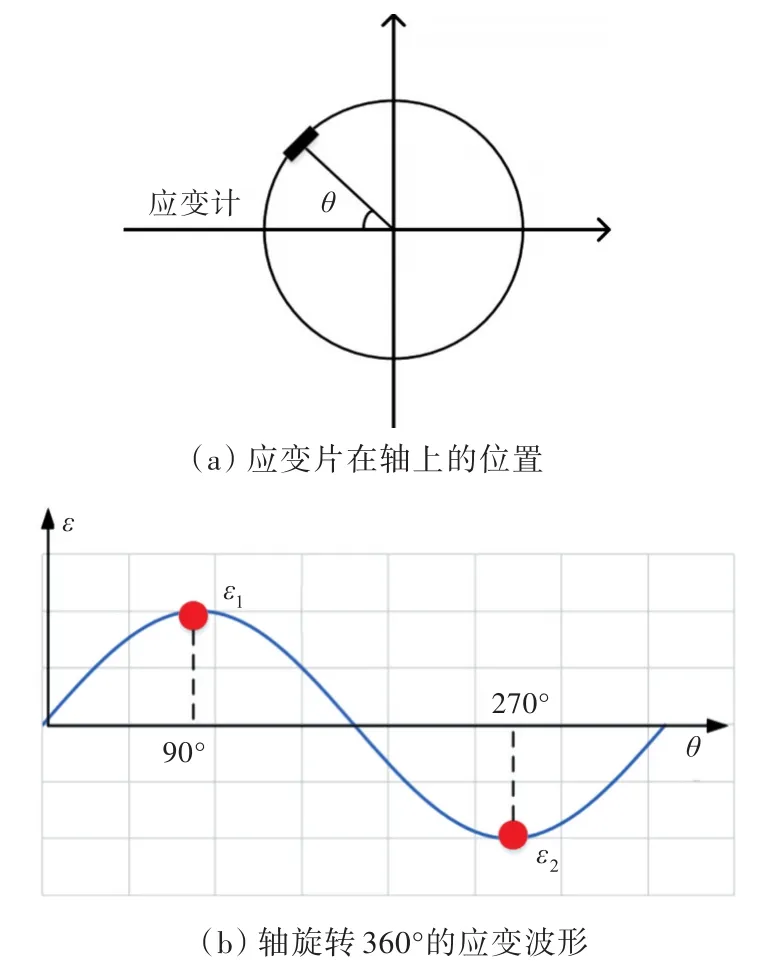
圖7 軸上彎矩測量原理Fig.7 Principle of measurement for bending moment on shaft

若考慮橫向彎曲，則應變的最大、最小值不出現在90°與270°，而是偏離一定的相位，但應變的幅值不會發生變化。

軸上的彎矩可以用式（8）來計算［9］：

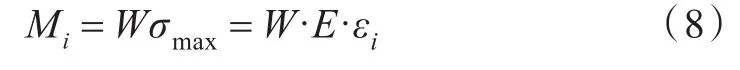
式中：Mi為測量截面i處的彎矩，kN·mm；σmax為測量截面i處的最大彎曲應力，GPa；W為測量截面i處的抗彎截面模數，mm3；E為軸系材料的彈性模量，GPa；εi為測量截面i處最大彎曲應變。

彎矩測量具體步驟為：

1）將主機第一缸盤車至上止點位置；

2）在軸上0°與180°位置粘貼2組應變片，組成惠斯通半橋橋路，再將測量電路與數據采集系統連接；

3）利用盤車機將主機盤車一周，同時開始采集數據；

4）利用動態信號采集分析系統對測量數據進行分析，計算各測點的彎矩值。

3.2 模型建立與測點布置

38 500 DWT散貨船為雙艉軸承軸系，包含1道中間軸承和6道主機軸承，因此需要的有效測點數為3。為驗證不同測點位置測得的彎矩對計算結果的影響，在軸上布置了5處測點，將5個測點按每組3個進行組合，可以得出9組逆計算結果。圖8為現場布置測點和粘貼應變片的照片，圖9為5處測點在軸上分布的示意圖。實驗測得的5個測點的彎矩值如表1所示。

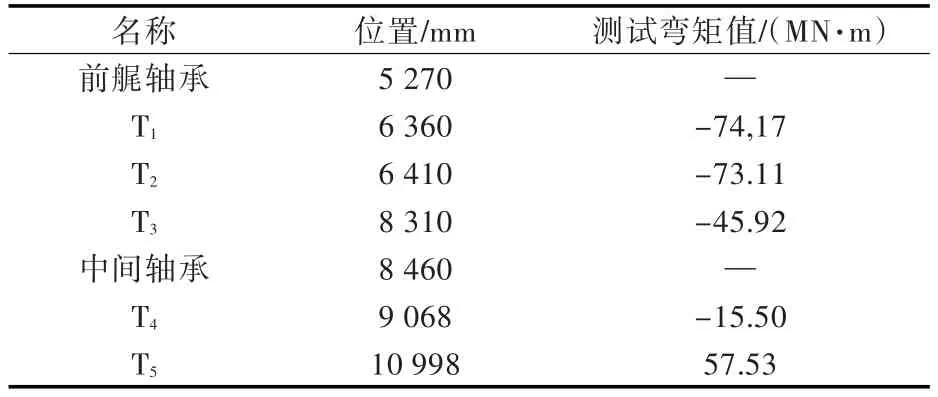
表1 38 500 DWT散貨船軸系應變測試結果Table 1 Tested strain of 38 500 DWT bulk carrier

根據測點彎矩值將測點組合后計算出9組變位，如圖10所示。

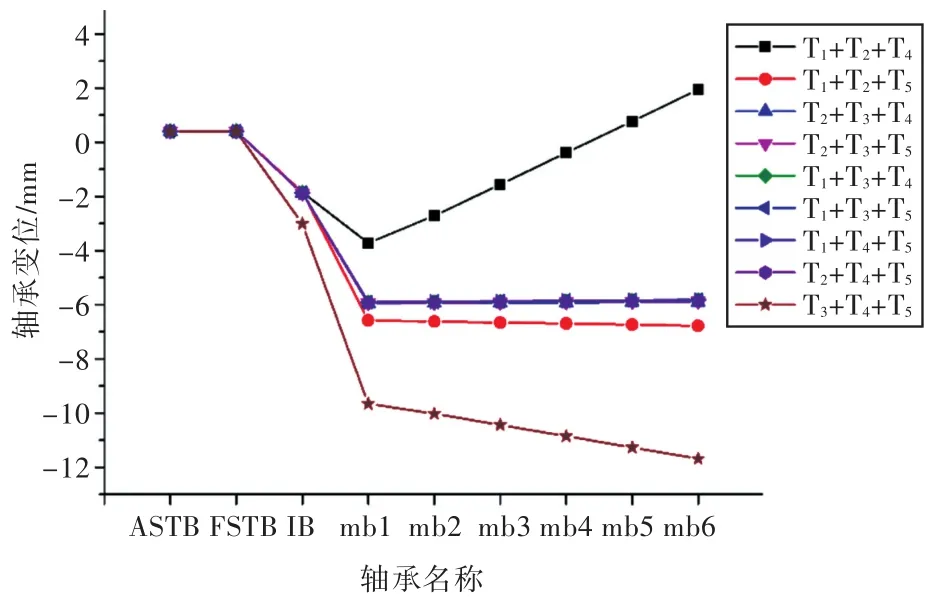
圖10 軸承變位逆計算結果Fig.10 Recalculated bearing offsets

各組合求解矩陣的條件數如表2所示。可見，T1+T2+T4，T1+T2+T5與T3+T4+T5這3組的條件數比其他組大了1～2個數量級，求解矩陣誤差敏感度上升，這是因為1號與2號測點相互距離很近、3號測點與中間軸承距離很近。結果T1+T2+T4與T3+T4+T5這2組結果非常不合理，T1+T2+T5組結果也存在較大誤差。

去除這3組結果，將其余結果取平均值作為最終結果輸出，計算各軸承負荷，如表3所示。

從表3中可以看出，計算負荷與頂舉負荷誤差最大為3.14%，第1道主機軸承計算為負值，而在實際頂舉中也是脫空狀態。圖11為根據軸承變位計算所得各截面的剪力、彎矩、撓度、轉角，可以為全部評估軸系安裝狀態提供參考。

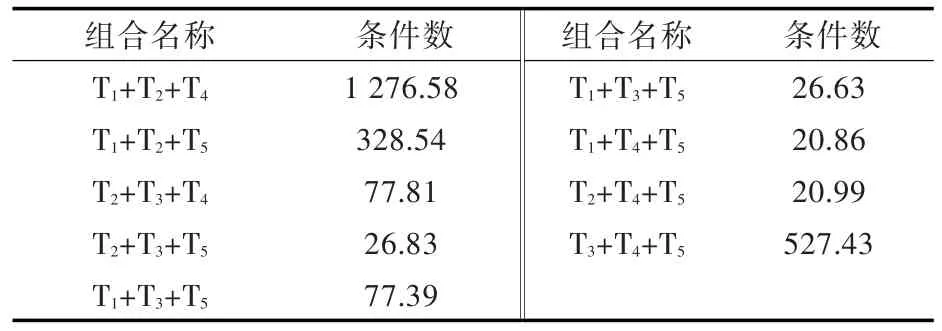
表2 各測點組合求解矩陣條件數Table 2 The condition number under different combinations of measuring points

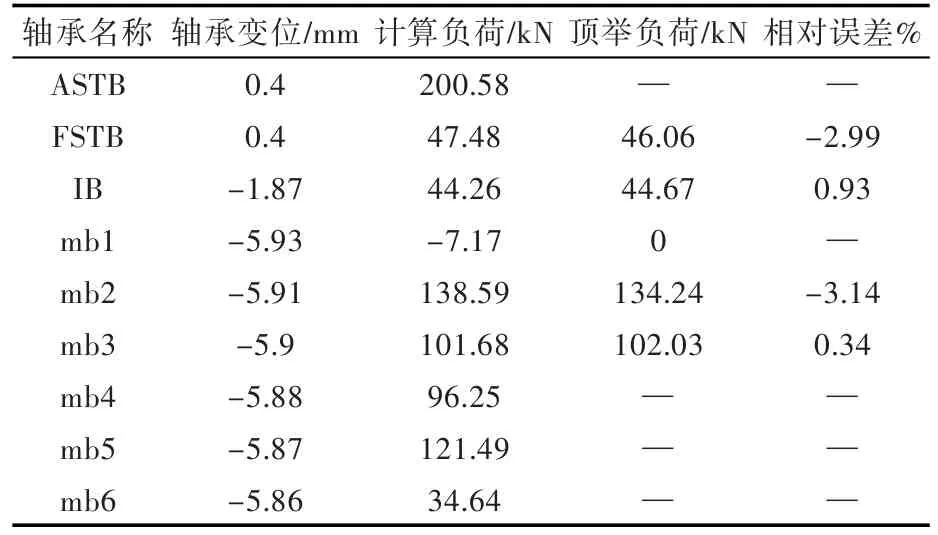
表3 軸承負荷計算結果Table 3 Calculation results of bearing load

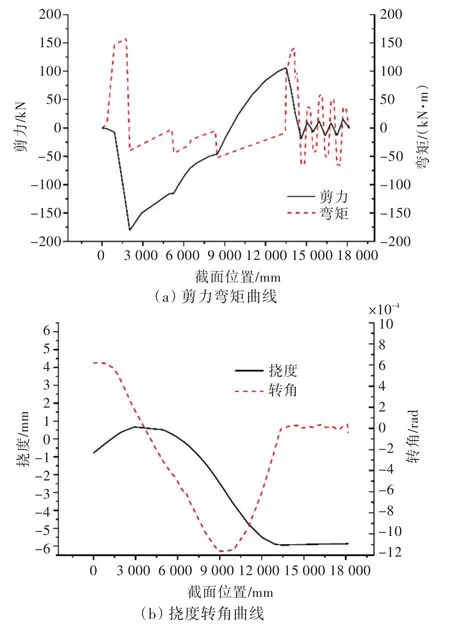
圖11 剪力彎矩及撓度轉角圖Fig.11 Plot for recalculated sheer force，bending moment，deflection and slope on shaft

4 結 語

軸系安裝后，獲得其準確的安裝狀態對于安裝質量的評估非常重要。本文提出的基于彎矩影響系數的逆計算方法相比傳統方法可獲得軸系的完整狀態，在軸系安裝未達標時，其計算出的軸承變位可以為下一步調整提供依據，同時計算出的剪力、彎矩、轉角等數據也可對軸系受力狀態作更全面的分析。實驗結果驗證了文中計算方法和測點布置原則的正確性。相比盤車工況的相對靜止狀態，軸系在實際運轉過程中的受力情況將更加復雜，運用無線應變檢測技術對軸系實際運轉狀態的監測是今后很有價值的研究方向。