基于實數全息圖的無零級光全息顯示技術

楊靖宇

（四川大學，成都 610065）

1 引言

由于零級光占有全息圖再現時大部分的光強。消除全息顯示系統中的零級光一直都是全息界的熱點話題。如果能夠設計出無零級光的全息系統，也就能夠獲得高效率，高亮度的全息圖。

2 計算全息術濾波的局限

計算全息中的數字濾波技術能夠同時消除零級光和共軛光，在計算機上生成只含有正1級光（目標圖像）的再現結果。然而，這樣濾波得到的頻譜如果變換回全息圖得到的是復數型全息圖。由于缺乏顯示復數型全息圖的空間光調制器，這樣的數字全息系統是無法搭建的。相比之下，實數型全息圖則更有潛力。

3 實數全息圖

將全息圖的頻譜域的-1級光和0級光濾去。得到的新頻譜逆傅里葉變換回全息圖。取新全息圖的實部得到有正負取值的全息圖。

式中，IH指原全息圖；F（）為傅里葉變換；P0為濾波函數；F-1為逆傅里葉變換；Re為取實部。采用離軸全息，以四川大學校徽為例，在MATLAB上制作出實數全息圖。程序如附錄所示。首先，用fft2（快速傅里葉變換）計算原始圖像的菲涅爾衍射。這里采用的計算方法是[1]中提到的S-FFT算法。然后設置一個與物光傳播方向有恰當夾角的參考光，計算物光與參考光的干涉。將干涉的復數結果取振幅得到全息圖。再用快速傅里葉變換計算該透過率為正實數的全息圖的頻譜。將頻譜-1級和0級所在的位置取為0。然后逆傅里葉變換得到一個復數全息圖，取復數全息圖的實部得到實數全息圖。

圖1 原始圖像

圖2 濾波前全息圖

其中歸一化頻譜＞1/10部分皆顯示為白色，濾波操作濾去了左上角的-1級頻譜和中央的0級頻譜。如圖6所示，用bar3函數展示了100個像素點的全息圖。由于濾波后取實部的全息圖有正負取值，因此用imshow（）無法體現全息圖的正負性，在這里使用bar3函數，bar3繪圖在1024*1024像素的情況下會給計算機很大的負擔，因此只取其中10000個像素顯示。

圖3 濾波前全息圖再現結果

圖4 濾波前頻譜

圖5 濾波后頻譜

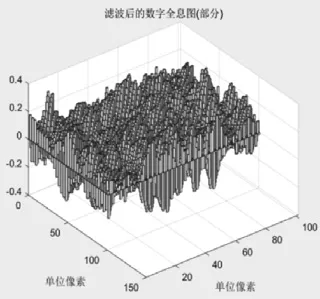
圖6 濾波后取實部的全息圖

圖7 實數全息圖的再現像

IH′作為有正負取值的實數全息圖，其正負取值剛好使得通過其的光場在光線傳播方向（0級光方向）完全干涉相消。如果將這樣的實數全息圖變換到頻域可以看到其頻域只含有右下和左上的點。這剛好對應了±1級像。

4 顯示實數全息圖的空間光調制器

數字全息顯示系統中，數字微鏡器件DMD（Digital Micromirror Device）是最常用的空間光調制器。DMD利用反射鏡面的翻轉來實現光開關的“開”、“關”狀態。再通過PWM波控制開關速率，快速開閉的反射鏡面利用人眼的視覺暫留產生灰度圖像。

圖8 數字微鏡器件

如圖8所示，為了實現反射鏡面的受控翻轉，數字微鏡陣列包含了3個部分-電路部分，機械部分，以及光學部分。其正常工作時，最下層的數字微鏡單元電路產生驅動信號，驅動信號使得中間層的機械部分運轉，帶動鉸鏈翻轉最上層的反射鏡面。然而，這樣的數字微鏡陣列僅能實現正實數透過率的全息圖。對于有正負取值的實數全息圖，由eiπ=-1，要實現負值則需使得光線產生π的相位差。

產生π相位差有如下幾個方法：

（1）制作新型空間光調制器。如果能夠在DMD的機械部分增加一個前后推動的微細推手，使得該推手接收驅動信號后將其前方的反射鏡面向前推移1/4個波長，經反射后也就與其他位置的光產生了·2=π的位相差了。

（2）利用半波損失。當光從折射率小的光疏介質射向折射率大的光密介質時，反射光相對于入射光有π的位相突變。如果將兩個DMD互成一定角度，其中一個DMD為主DMD，激光源發射的光入射到該DMD后反射到±12°的方向。±12°為觀察方向，-12°方向設置另一個DMD，其距離主DMD整數個波長，調整其在水平面的角度，使得其反射到-12°方向的光剛好投射到屏上，與原DMD的±12°光發生干涉，-12°光因為2次反射而與±12°擁有π的位相差，從而干涉相消，消除掉0級光。

（3）利用相位型衍射光學元件。如果在DMD表面放置一個二元相位型的衍射光學元件。該二元衍射元件階梯高度為也能產生π的相位差。該相位型衍射光學元件可由普通光刻機簡單地制作出來，對光刻精度要求很小，但僅限于靜態全息。title（‘物平面重建圖像'）；axis square。