類星體長周期光變分析方法的研究*
余 蓮,張 雄,張皓晶,李富婷,徐小林,任國偉,吳月承
(云南師范大學物理與電子信息學院,云南 昆明 650500)
對長周期光變的研究是分析耀變體性質的重要方法之一,它的確定關系到耀變體的結構和輻射等相關的多個物理量的估算,比如輻射區域的半徑、噴流的多普勒因子和黑洞質量等,長周期光變為理論模型的建立提供一定的參數。光變可分為長時標光變、中等時標光變、短時標光變[1]。對于長時標光變和中等時標光變來說,由于受到觀測儀器、月相和天氣等多種因素的影響,很難得到比較完整的光變的觀測數據序列[2]。在研究光學劇變類星體光變周期性時,通過研究長周期光變分析方法,可以獲取周期光變分析的最佳參數,用有限的實際觀測數據序列獲得最佳周期估算值。
通常分析周期的方法有:功率譜法、Jurkevich方法、小波、結構函數等,這些方法的特點是可以對高于奈奎斯特采樣定律均勻采樣的數據進行可靠分析[3-5]。但是實際的數據分析,特別是針對天體觀測所獲得耀變體的長時標光變周期分析中,這些方法的使用受到許多條件的限制,比如說傅里葉分析[6]要求連續的等間隔采樣,缺失數據點的處理引進了一些不真實的信息。所以這些方法應用在天體的光變周期分析中,增大了確定周期的誤差。而文[7]提出的Jurkevich方法,是一種建立在期待值均方誤差基礎上的統計方法,對于處理不等間隔觀測數據有很大幫助[7]。本文利用4種方法對這一問題進行討論,并提出相應的改進,使得在不等間隔時間序列的類星體光變曲線中,尋找周期性的分析計算變得更為簡便準確。
1 類星體長周期光變的計算方法
1.1 Jurkevich方法

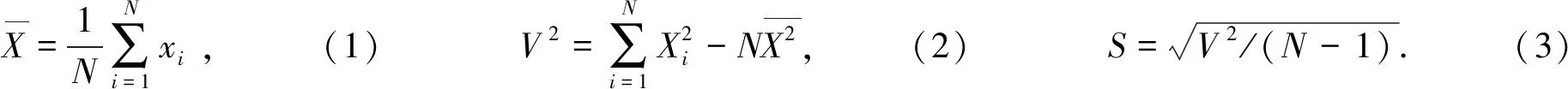

(7)
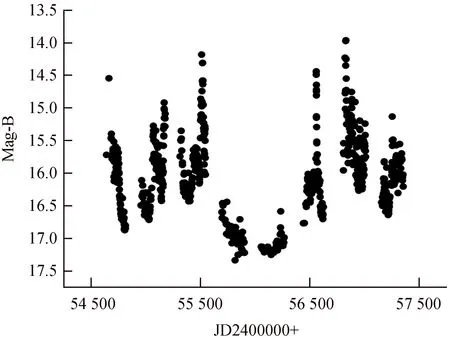
顯然,V2m 在周期分析中按照不同的試驗周期P把數據折疊,然后把折疊好的資料按相位從小到大排列,分成m組。若給定一個觀測時間為t,試驗周期為P,則其對應的相位定義為[7] (8) 其中,φ(t)滿足0≤φ(t)≤1;t0為時間原點。計算出每組數據的方差V2l和總方差V2m,如果所得的實驗周期等于實際周期,則V2m的值將達到最小,由實驗周期Pn與V2m的關系曲線中的V2m最小值對應的時間即可得到樣本的周期。 時間補償離散傅里葉變換方法是計算光變周期最常用的方法之一,此方法最早由文[9]在1981年提出。在過去的研究中文[10]用該方法分析PKS 1510-089紅外光變周期。通過對1,sinωt,cosωt作Gram-Schmidt正交化,得到3個正交向量,將數據投影到3個正交向量上得到了頻譜。具體過程如下: H0=1;H1=cosωt;H2=sinωt. (9) 正交化后:h0=a0H0, (10) h1=a1H1-a1a0(h0,H1), (11) h2=a2H2-a2a0(h0,H2)-a2a1(h1,H2), (12) 小括號表示求兩個向量的內積。根據以下關系確定h0,h1,h2: (h0,h0)=(h1,h1)=(h2,h2)=1 . (13) 在不均勻采樣的情況下,加權的時間補償離散傅里葉變換: (14) 在許多類星體的觀測中,觀測數據f(ti)的精度各不相同,考慮到這個問題,引進權重方程ωi=ω(ti),重新定義內積: (g1,g2)=∑ωig1(ti)g2(ti). (15) (16) (17) (18) 在內積中引入權重后得到回歸系數:c0=0, (19) c1=a1∑ωif(ti)cosxi, (20) (21) (22) 由線性回歸理論可知0≤I(ω)≤Q,式中: Q=(f,f)=∑ωif(ti)2, (23) 利用這一性質,引進標準化因子:統計量S(ω)=I(ω)/Q,稱這個量為譜相關系數,對于所有頻率ω,0≤S(ω)≤1。 離散相關分析方法是Edelson和Krolik用來分析兩組離散數據相關性的方法之一,文[11]用此方法分析PKS 2155-304的光變。該方法可以指出兩個變量時間序列的相關性和時間延遲,并可應用于周期性分析[11]。具體步驟如下: 首先計算兩組數據的離散相關函數值,如數組ai和bi,則離散相關函數值為 (24) 其次,計算DCF(τ)值。通過時間延遲Δtij=ti-tj把兩組數聯系起來,假如時間延遲為τ,在區間τ± Δτ/2中有M個Δtij,則DCF(τ)值為 (25) 再次離散相關函數的誤差為 (26) 對于所得到的離散相關圖,如果峰值在0的右邊,表明數組ai早于數組bi的變化。反之,數組ai遲于數組bi的變化。 功率譜密度的定義[12]是如果u(t)是一個可以進行傅里葉變換的函數,則 u(ν)=∑u(t)e-2icvt, (27) 因為u(t)是實函數,u(ν)是一個復函數,它們之間滿足Parseval公式 (28) 若u(t)表示光譜,則等式左端表示u(t)在(-,)上的總能量,右端的函數稱為能譜密度,它是一個非負實數,表示單位頻率所具有的能量。從數學意義上講,大多數u(t)不能進行傅里葉變換,如果使用截尾函數ur(t)截取u(t), (29) 那么對于持續時間有限的截尾函數ur(t)而言可以進行傅里葉變換,變換式: uT(ν)=∑uT(t)e2icνt=∑u(t)e2icνt, (30) (31) 根據截尾函數的定義,將上式兩端除以2T并令T→,得到 (32) 與能譜密度的定義相對應,上式右端函數稱為功率譜密度,記為 (33) 從表達式中可見功率譜密度是一個非負實數,從整個功率譜密度的推導可以看出,功率譜密度是一個頻域中的量,它直接反應了在頻域中不同頻率對應的值。 為檢驗上述4種研究方法的可靠性,用一個模擬的周期信號作為天文觀測數據分析上述4種方法。在這里以2π為周期的正弦函數y=sinθ,檢驗分析4種研究方法的準確性,使用的單位為弧度。在實驗中選擇0 rad為起點,步長為0.1 rad,不同的數據點個數共取15組,所有研究方法考慮噪聲等因素的影響。 圖1為檢驗Jurkevich方法分析天體周期的可靠性,取80~360個數據點,每組增加20個數據點,通過Jurkevich方法分析后得到15組不同數據點的V2m-P曲線,進而得到的分析結果為(6.30 ± 0.02) rad。 圖1 Jurkevich方法對sin函數不同數據點的周期性分析 圖2為檢驗時間補償離散傅里葉變換分析方法分析天體周期的可靠性,取80~360個數據點,每組增加20個數據點,用時間補償離散傅里葉變換分析方法分析后得到15組不同數據點的DCDFT-Frequency曲線,進而得到的分析結果為(6.33 ± 0.13) rad。 圖2 時間補償離散傅里葉變換分析方法(DCDFT)對sin函數不同數據點的周期性分析 圖3為檢驗離散相關分析方法分析天體周期的可靠性,取80~360個數據點,每組增加20個數據點,用離散相關分析方法分析后得到15組不同數據點的DCF-Delay曲線,進而得到的分析結果為(6.287 ± 0.088) rad。 圖4為檢驗功率譜密度分析方法分析天體周期的可靠性,取80~360個數據點,每組增加20個數據點,用功率譜密度分析方法分析后得到15組不同數據點的Power-Frequency曲線,進而得到的分析結果為(6.287 ± 0.045) rad。 由圖5得到,Jurkevich方法、時間補償離散傅里葉變換分析方法、離散相關分析方法和功率譜密度分析方法周期需要的數據點最低分別為50個、120個、100個和60個。獲取最短的連續數據采樣后,Jurkevich方法最有效。 圖3 離散相關分析方法(DCF)對sin函數不同數據點的周期性分析 如圖6,當取360個數據點,分組數為1~6組時,要求不等間隔的數據樣本周期數不少于6個[7],因此周期性可忽略;當分組數為7~12組時,在第10組、第11組和第12組可能出現了倍周期,即可能剛好是第1個周期的重復出現。即使出現極小微差的偽周期,周期性最好的仍為第9組。 當取720個數據點,如圖7,分組數為1~6組時,同樣沒有周期性;當分組數為7~12組時,在第10組和第12組出現了倍周期,即可能剛好是第1個周期的重復出現;在第11組出現了明顯的偽周期,因此第9組周期性的分析結果最佳。 如圖8,當取1 500個數據點,分組數為1~6組時,周期性不明顯,所以這幾組的周期可忽略。當分組數為7~12組時,在第8組、第10組和第12組出現了倍周期,第11組的周期性顯然沒有第9組明顯。總的來說,周期性的最佳分析結果為第9組。下面用具有多個觀測數據的兩個源驗證此結果。 圖4 功率譜密度分析方法(PSD)對sin函數不同數據點的周期性分析 圖5 sin函數用時間補償離散傅里葉變換分析方法 (DCDFT)、Jurkevich方法、離散相關分析方法 (DCF) 和功率譜密度分析方法 (PSD) 進行周期分析時要求的最低數據點 (右邊的兩個圖形從上向下分別為Jurkevich方法和功率譜密度分析方法(PSD) 的分析圖形) Fig.5 The minimum data points required for the sin function to perform periodic analysis using the DCDFT method, Jurkevich method, DCF method and PSD method (The two graphs on the right are the Jurkevich method and PSD method analysis graph from top to bottom) 圖6 sin函數的V2m-P,左圖分組數為1~6組,右圖分組數為7~12組 圖7 sin函數的V2m-P,左圖分組數為1~6組,右圖分組數為7~12組 圖8 sin函數的V2m-P,左圖分組數為1~6組,右圖分組數為7~12組 Fig.8 TheV2m-Pcurve of sin, The number of groupings on the left are Group 1-6,and the grouping on the right are Group 7-12 本文研究的類星體3C 279在B波段和3C 454.3在B波段數據點主要是從網站(http://www.astro.yale. 從2008年2月5日到2017年7月19日,由以上網站搜尋到類星體3C 279在B波段的數據點有661個,B波段的光變曲線如圖9,可以看出有幾次大的爆發,最亮時B波段星等為14.9,光變曲線中有6個以上周期存在,這些均滿足Jurkevich方法中確認長周期存在的必要條件[13]。 利用Jurkevich方法分組數m=9,圖10可得到3C 279在B波段的光變周期(2.81 ± 0.54)年。周期Pn與V2m的關系曲線中有很多的極小值,為了有效地判斷周期Pn與V2m關系曲線中所得出周期的真實性,文[14]給出了較好的判據: (34) 其中,V2m為歸一化的值。在歸一化的V2m-Pn圖中,若V2m=1.0,則有f=0,即在樣本數據中沒有表現出周期性;若V2m=0,則有f=1,這時樣本中存在的最大周期能夠從圖中識別。在通常情況下,當f≥ 0.5時,樣本數據表現出非常強的周期性;當f≤ 0.25時,則表現為不含有周期性。進一步分析V2m值,選擇曲線較平滑部分的最小深度和噪聲做實驗,如果平滑部分的相對最小爆發值比平滑部分的V2m大10倍,則可以進一步討論相應的短周期性。在計算中分組數m的大小十分重要,組數m分得越多,靈敏度越高,但每組數據中有少數的數據點在圖中產生較大的噪聲。分組數m較大時,還增加V2m的計算量。反之,有可能尋找不到周期。如圖10,對類星體3C 279在B波段的光變周期分析中,很容易找到V2m及P值,并用文[14]的判據:f=(1-V2m)/V2m進行檢驗,結果如表1。 通過對表1分析發現,最小值V2m=0.352 1,f=1.840 1,類星體3C 279可能的光變周期為(2.81 ± 0.54)年。利用Jurkevich方法,分組數m=9,分析了類星體3C 279在B波段的光變數據,圖10顯示了B波段的分析結果。從表1可以看出,在滿足判據f的條件下[14],類星體3C 279在B波段的P2,P3與P1之間存在類星體簡單的倍數關系:P2≈2P1,P3≈3P1,說明它們之間可能存在天文學倍頻關系。 圖9 類星體3C 279在B波段的光變周期 Fig.9 The light curve of quasar 3C 279 in B band 圖10 Jurkevich方法分析類星體3C 279在B波段的光變周期 Fig.10 Jurkevich method analysis of the variability period of quasar 3C 279 in B band 3C 454.3(PKS 2251+158, OY091)是一個比較亮、變化比較劇烈的類星體,并且在光學和射電波段存在比較明顯的相關性[15]。本文的數據是從2008年6月23日到2017年7月30日,約765個數據點,獲得了如圖11的歷史光變曲線。 利用Jurkevich方法,分組數m=9,分析了類星體3C 454.3在B波段的光變數據,圖12顯示了B波段的分析結果。從圖12可以看出,類星體3C 454.3在B波段有3個明顯的極小值,意味著類星體3C 454.3在B波段光變曲線中存在3個可能的周期,它們分別是:P1=457 d,P2=891 d和P3=1 320 d。根據文[16]的結果,要確定一個周期,數據樣本的時間跨度要超過周期的6倍。文中數據樣本的時間跨度大約2 500 d,小于P2,P3的6倍, 故P2,P3必須排除,并需要更多的觀測數據確定它們。但是P2,P3與P1之間存在著簡單的倍數關系:P2≈2P1,P3≈3P1,說明它們之間可能存在天文學倍頻關系,意味著類星體3C 454.3在B波段的光變曲線中可能存在一個P1=457 d的真正的光變周期。 表1 類星體3C 279在B波段的周期分析表Table 1 The table of 3C 279 objects cycle analysis 圖11 類星體3C 454.3在B波段的光變周期 Fig.11 The light curve of quasar 3C 454.3 in B band 圖12 Jurkevich方法分析類星體3C 454.3在B波段的光變周期 Fig.12 Jurkevich method analysis of the variability period of quasar 3C 454.3 in B band 如圖12,對類星體3C 454.3在B波段的光變周期分析中,很容易找到V2m及P值,并用文[14]的判據:f=(1-V2m)/V2m進行檢驗,結果如表2。 通過對表2分析發現,當V2m取最小值0.550 5,f=0.817,對應的光變周期可能為P=457 d,這既滿足了圖12的分析結果,也滿足f判據[14]。 表2 類星體3C 454.3在B波段的周期分析表Table 2 The table of 3C 454.3 objects cycle analysis 本文利用一個以2π為周期的正弦函數y=sinθ檢驗4種研究方法的可靠性。在實驗中,使用的單位為弧度,選擇0 rad為起點,步長為0.1 rad,不同的數據點個數共取15組,得到Jurkevich方法的分析結果為(6.3 ± 0.017) rad;時間補償離散傅里葉變換分析方法的分析結果為(6.331 ± 0.130) rad;離散相關分析方法的分析結果為(6.287 ± 0.088) rad;功率譜密度方法的分析結果為(6.287 ± 0.045) rad。分析結果表明,Jurkevich方法、時間補償離散傅里葉變換分析方法、離散相關分析方法和功率譜密度方法周期需要的數據點最低分別為50個、120個、100個和60個。獲取最短的連續數據采樣后,Jurkevich方法最有效。Jurkevich方法分析結果在4種方法中最精確可靠,且此計算方法簡捷實用。 在實際應用中,發現Jurkevich方法十分依賴于分組數m,m越大分析結果越好,但會產生比較大的噪聲;反之則有可能找不到周期[17]。如果數據分布不均勻,則會導致組間數據分布偏差很大,從而影響獲得實際的周期。根據圖6、圖7和圖8可以看出,對于不同的m值,V2m與Pn的關系曲線的傾斜程度不同,周期大的向下傾斜。結合f檢驗公式可知,V2m越小,f值越大,更容易滿足f檢驗。由此可知f檢驗依賴于m值的大小。利用模擬數據尋找到Jurkevich方法的分組數為m=9時,分析結果最佳。最后用分組數m=9時的Jurkevich方法分析了類星體3C 279及3C 454.3的光變周期,得出類星體3C 279可能的光變周期為(2.81 ± 0.54)年,在文[18]中分析了類星體3C 279可能的光變周期為(130.6 ± 1.3) d,分析得到的可能周期大約是(130.6 ± 1.3) d的8倍。類星體3C 454.3可能的光變周期為457 d。在文[19]中分析了類星體3C 454.3可能的光變周期為12.39年,大約是本文得到周期的10倍。1.2 時間補償離散傅里葉變換分析方法

1.3 離散相關分析方法
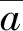
1.4 功率譜密度分析方法
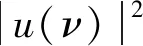

2 天文觀測數據中周期信號的模擬檢驗
2.1 天文觀測周期信號的模擬檢驗結果

Fig.1 Periodic analysis of sin functions′ different data points by using Jurkevich method
Fig.2 Periodic analysis of sin functions′ different data points by using DCDFT method2.2 利用天文模擬數據尋找Jurkevich方法的最佳參數

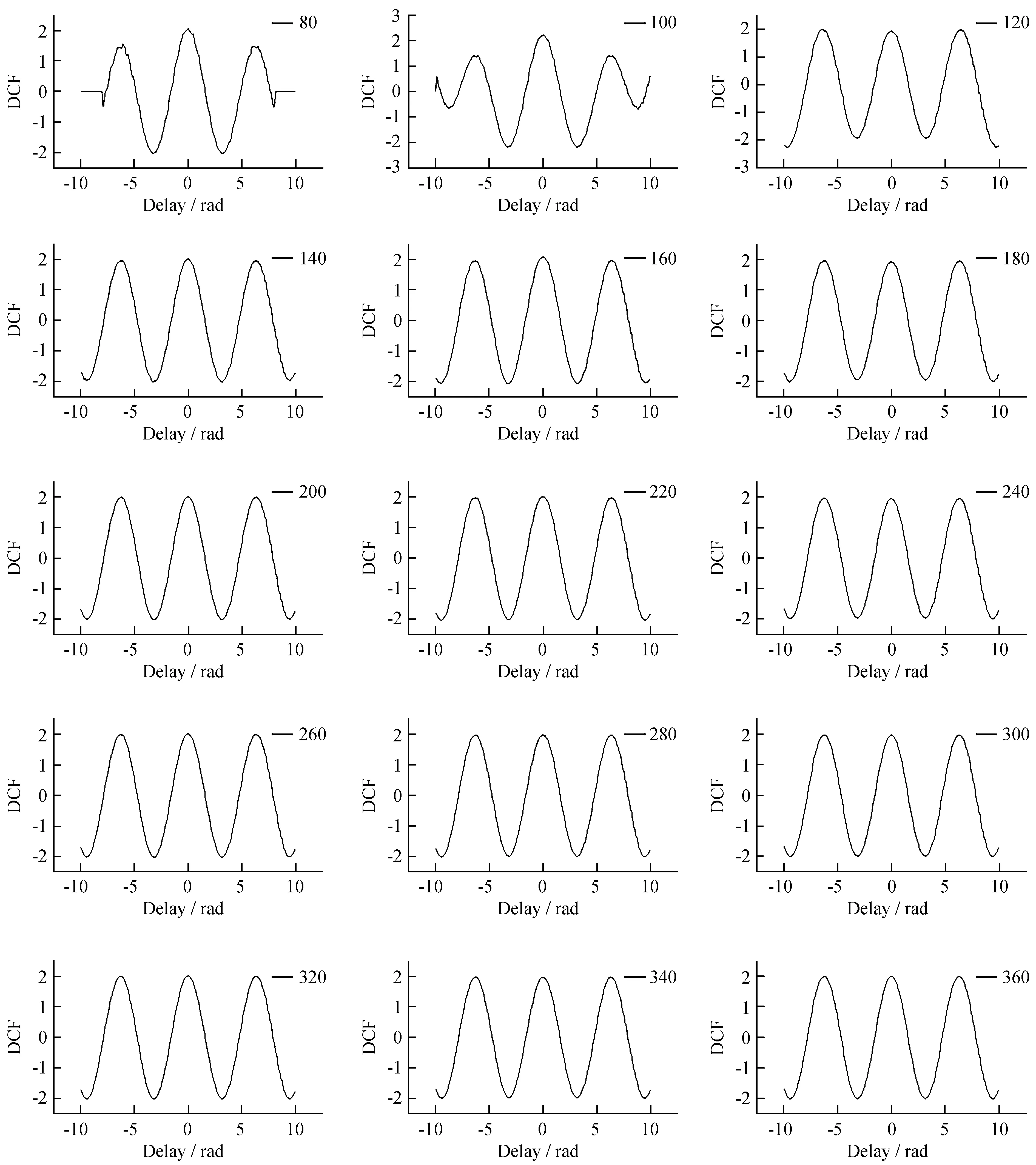
Fig.3 Periodic analysis of sin functions′ different data points by using DCF method
Fig.4 Periodic analysis of sin functions′ different data points by using PSD method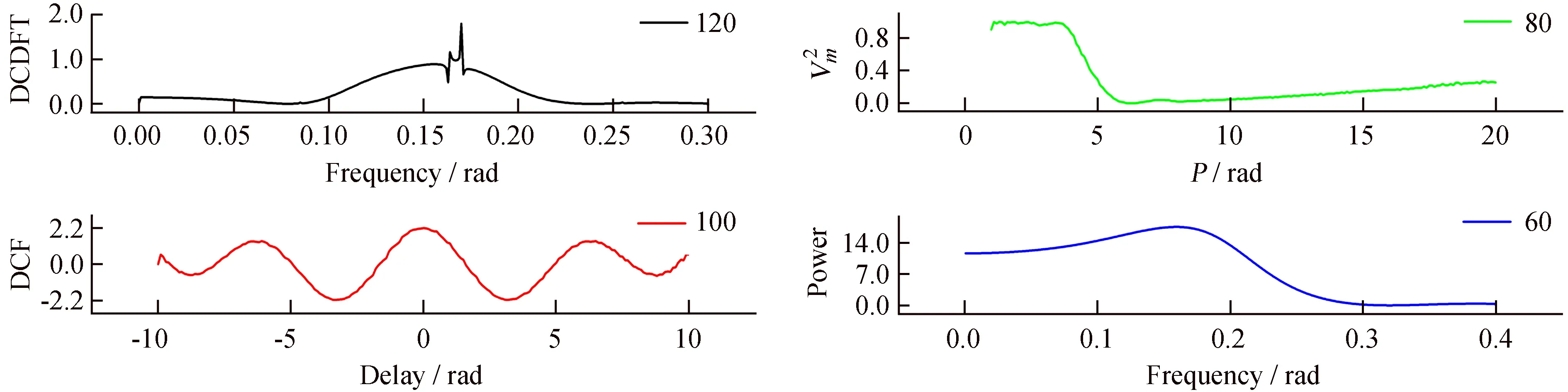

Fig.6 TheV2m-Pcurve of sin, The number of groupings on the left are Group 1-6, and the grouping on the right are Group 7-12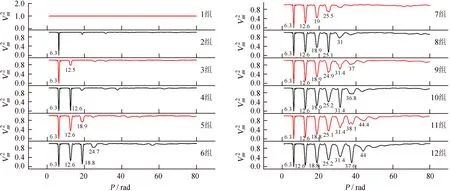
Fig.7 TheV2m-Pcurve of sin, The number of groupings on the left are Group 1-6, and the grouping on the right are Group 7-12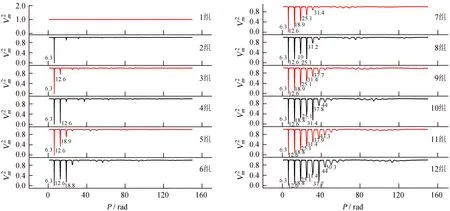
3 計算并分析類星體3C 279和3C 454.3的光變周期
3.1 類星體3C 279的數據點及光變周期
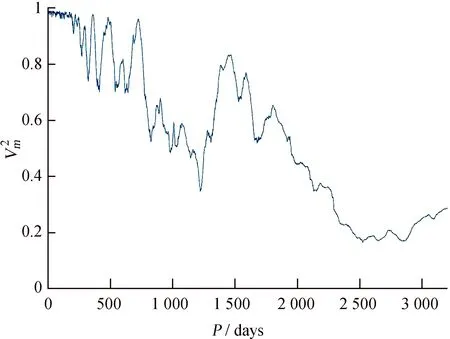
3.2 類星體3C 454.3的數據點及光變周期



4 討論與結論

