關于指數Diophantine方程x2=D2m?Dmpn+p2n

賀艷峰

(延安大學數學與計算機科學學院,陜西延安 716000)

1 引言和結論

設Z,N分別是全體整數和正整數的集合.D>1是正整數,p是適合p-D 的素數.50多年前,陳景潤[1]在研究數論中有關本原商高數的Je?manowicz猜想時,曾涉及到方程

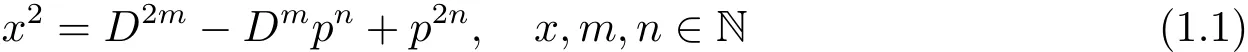
的求解問題.這是一類指數型的廣義Ramanujan-Nagell方程,它與數論、組合數學和編碼理論中的很多重要問題的研究有關(參考文獻[2]).對此,佟瑞洲在文獻[3]中確定了方程(1.1)的所有適合m=1的解(x,m,n);在文獻[4]中提出,除了

以外,方程(1.1)適合m>1的解必定滿足下列兩個條件之一:

(i)D是奇數,p≡1(mod 8),m=2,n=1;

(ii)D是偶數,D含有2kq+1之形素因數,其中q是m的奇素因數.然而,方程(1.1)除了(1.2)以外,顯然還有解

不滿足上述(i)和(ii).由此可知文獻[4]的結果是不完整的.

對于非負整數t,設

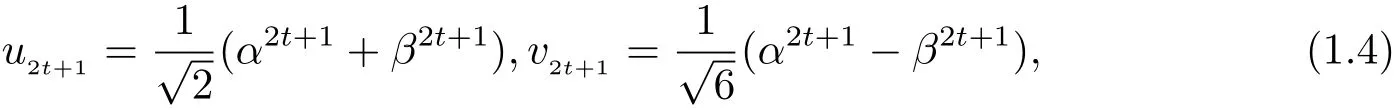
其中

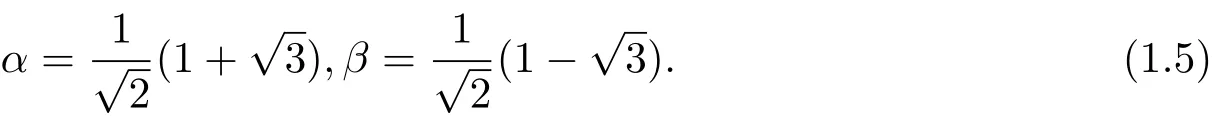
本文根據Diophantine方程的性質和若干已知結果,運用初等方法,完整地確定了方程(1.1)適合m>1的所有解,即證明了

定理 除了(1.2)和(1.3)以外,方程(1.1)適合m>1的解僅有

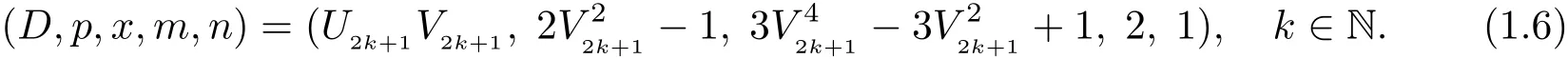
2 若干引理

為了證明定理,首先需要證明下面的幾個引理.為此,設X>1,r>1均是正整數,q是奇素數.

引理 2.1如果 Xr?1是素數,則X=2且r是素數.

證 參見文獻[5]的定理1.10.1.

引理 2.2 如果Xr+1是素數,則X是偶數且r=2s,其中s是正整數.

證 參見文獻[5]的定理1.10.2.

引理 2.3設X>1,r>1均是正整數,q是奇素數,則

(i)

(ii)當X+1≡0(mod q)時,q k(Xq+1)/(X+1),且(Xq+1)/q(X+1)的素因數p滿足p≡1(mod 2q);當X+1 6≡0(mod q)時,(Xq+1)/(X+1)的素因數p滿足p≡1(mod 2q).

證 參見文獻[6].

引理 2.4當 U2t+1,V2t+1適合(1.4)和(1.5)式時,(U,V)=(U2t+1,V2t+1)(t=0,1,···)是方程

的全部解.

證 因為(U,V)=(1,1)是方程(2.1)的最小解,所以從文獻[7]第5.3節直接可得本引理.

引理2.5方程組

僅有解(X,Y,Z)=(1,1,1).

證 參見文獻[4]的引理6.

引理2.6方程

僅有解(X,Y)=(1,1).

證 參見文獻[7]第6.2節.

引理2.7方程

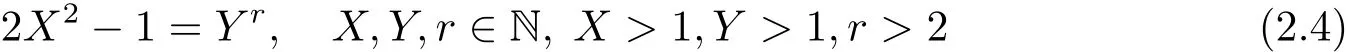
僅有解(X,Y,r)=(78,23,3).

證 參見文獻[8]的定理8.1.

引理2.8方程

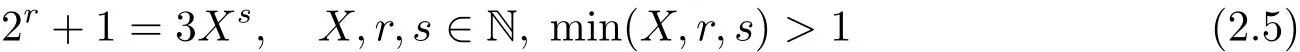
無解(X,r,s).

證 參見文獻[9].

引理2.9方程

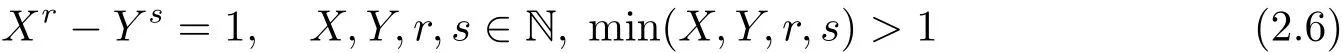
僅有解(X,Y,r,s)=(3,2,2,3).

證 參見文獻[10].

引理2.10對于奇素數p,方程

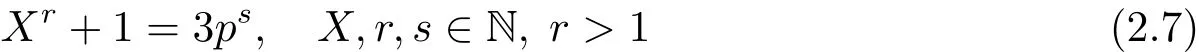
證 設(p,X,r,s)是方程(2.7)的一組解.此時顯然X>1.因為當r是偶數時,3-Xr+1,所以r必為奇數;又因r>1,所以r必為奇素數q.

根據引理2.9可知,方程(2.7)僅有解(p,X,r,s)=(3,2,3,1)適合p=3.當p 6=3時,因為從方程(2.7)可知3|Xr+1且32-Xr+1,所以q>3.設

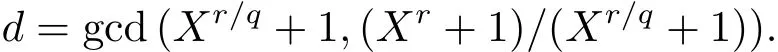
根據引理2.3,從(2.7)式可知d=1或p且q=p.

如果d=1,則從(2.7)式可知

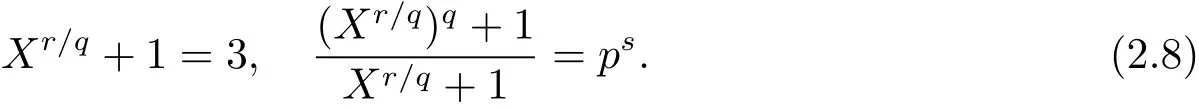
由于從(2.8)式中第一個等式可得X=2,且r=q,又結合引理2.8和(2.8)式的第二個等式可得s=1,故有其中q是大于3的奇素數.

如果d=p,且q=p,則根據引理2.3的結論(ii),從(2.7)式可得Xr/q+1=3ps?1≥3p,以及p=(Xr+1)/(Xr/q+1)>Xr/q+1>p,這就得出一對矛盾不等式,故d=p不成立.引理證完.

引理2.11對于奇素數p和q,方程

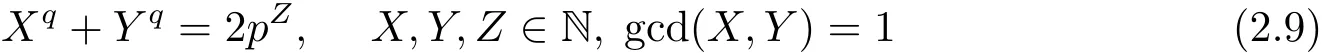
無解(X,Y,Z).

證 設(X,Y,Z)是方程(2.9)的一組解.因為p>1,所以(X,Y)6=(1,1),故有X+Y>2.由于(Xq+Yq)/(X+Y)是大于1的奇數,所以從(2.9)式可得

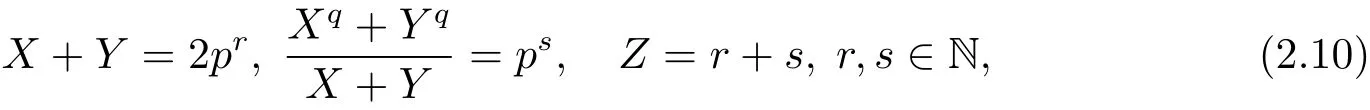
因為從(2.10)式可知p|gcd(X+Y,(Xq+Yq)/(X+Y)),所以q=p.然而,由于q k(Xq+Yq)/(X+Y),所以(2.10)式中的 s=1,并且可得q=p=(Xq+Yq)/(X+Y)>q,矛盾.因此方程(2.9)無解.引理證完.

引理2.12當r是大于2的正整數時,方程

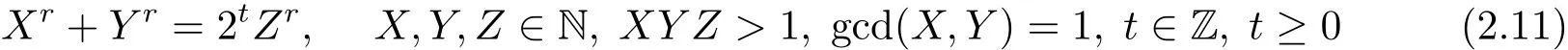
無解(X,Y,Z,t).

證 參見文獻[11].

3 定理的證明

設(x,m,n)是方程(1.1)的一組滿足m>1的解.

首先討論p=2時的情況.此時D是大于1的奇數,方程(1.1)可表示成

因為D是奇數,所以從(3.1)式可知x也是奇數,故從x2≡D2m≡1(mod 8)以及0≡x2?D2m≡?2n(Dm?2n)(mod 8)可知n≥3.

從(3.1)式可得

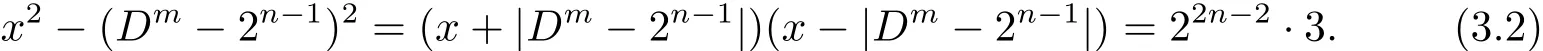
因為gcd(x+|Dm?2n?1|,x?|Dm?2n?1|)=2,所以從(3.2)式可得

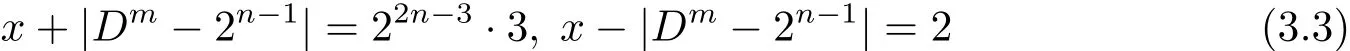
或

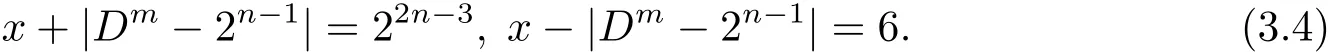
當(3.3)式成立時,在其中消去x可得

由于 n ≥ 3,所以 22n?4·3?1>22n?3>2n?1,故從 (3.5)式可知 Dm>2n?1以及

從(3.6)式可得

因為n≥3,所以從(3.7)式可知m必為奇數,故有m≥3.又因(Dm+1)/(D+1)是奇數,所以從 (3.7)式可得 D+1 ≥ 2n?1,以及 2n?1>2n?3·3+1 ≥ (Dm+1)/(D+1)≥(D3+1)/(D+1)=D2?D+1>D+1≥2n?1這一矛盾.

當(3.4)式成立時,在其中消去x可得

如果n=3,則從(3.8)式可得|Dm?4|=1.然而,因為m>1,這是不可能的.如果n>3,

則因 22n?4?3>2n?1,所以從 (3.8)式可知 Dm>2n?1以及

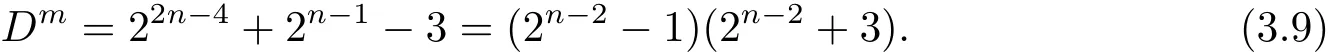
由于 gcd(2n?2?1,2n?2+3)=1,故從 (3.9)式可得

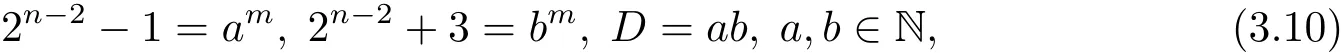
然而因為m>1,所以根據引理2.9,從(3.10)式中第一個等式可知n=3,又從第二個等式可得bm=5這一矛盾.

從以上分析可知,當p=2時,方程(1.1)沒有適合m>1的解(x,m,n).

其次討論p是奇素數時的情況.此時從(1.1)式可知

因為p-D,所以p-x且gcd(2x+|2Dm?pn|,2x?|2Dm?pn|)=1,故從(3.11)式可得

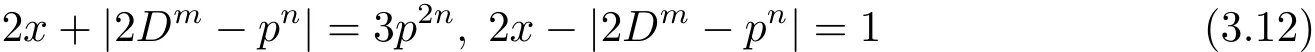
或

現分別按照(3,12)式和(3.13)式成立這兩種情況進行討論.

情況I(3.12)式成立.從(3.12)式可得

和

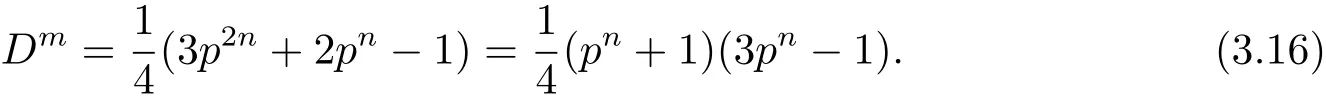
如果pn≡1(mod 4),則因與是互素的奇數,故從(3.16)式可得

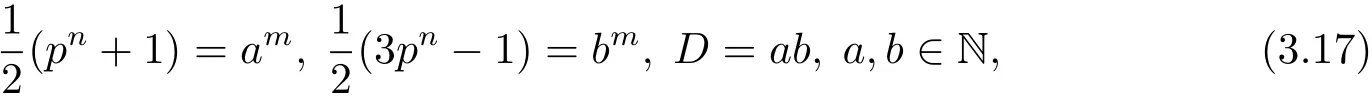
從(3.17)式可得

和

由于m>1,根據引理2.11,從(3.18)式可知m沒有奇素因數,所以m=2s,其中s是正整數.同時,因為從(3.18)式可知(a,b)6=(1,1),所以根據引理2.6,結合(3.19)式可知s<2.因此s=1,即m=2.將此代入(3.17)式中第一個等式,可得

當n>2時,根據引理2.7,結合(3.20)式可知,僅有(a,p,n)=(78,23,3),然而,此時從(3.17)式中第二個等式可得=18250,故這是不可能的.

當n=2時,聯合(3.19)式和(3.20)式可知,方程組(2.2)有解(X,Y,Z)=(p,a,b)6=(1,1,1).然而,根據引理2.5可知這是不可能的.

當n=1時,根據引理2.4,聯合(3.14),(3.19)和(3.20)式可得形如(1.6)式的解.

如果pn≡3(mod 8),則因是與3pn?1互素的奇數,后者是偶數,所以從(3.16)式可得

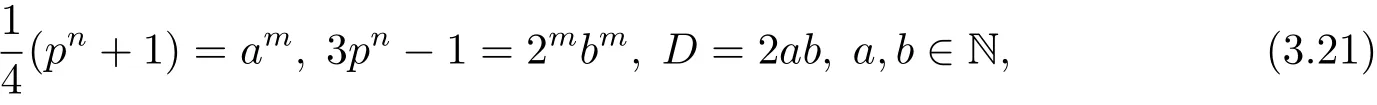
因為m>1,所以根據引理2.10,從(3.21)式中第二個等式可得

或

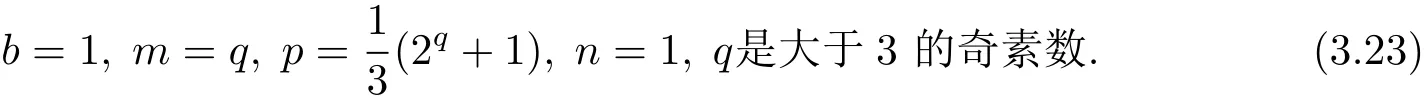
當(3.22)式成立時,聯合(3.14)和(3.21)式可得解(1.2).當(3.23)式成立時,從(3.21)式中第一個等式可得

如果pn≡7(mod 8),則因是與pn+1互素的奇數,后者是偶數,所以從(3.16)式可得

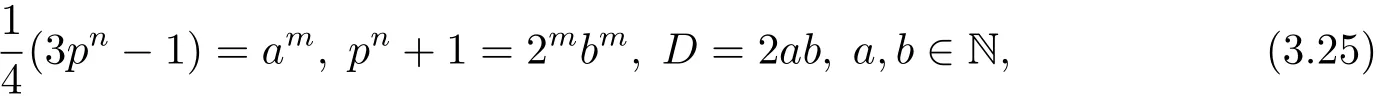
因為m>1,所以根據引理2.9,從(3.25)式中的第二個等式可知n=1,以及

再根據引理2.1,從(3,26)式可知b=1.將此代入(3.25)式中的第一個等式可得

然而,由于1<3·2m?2?1<2m,所以(3.27)式不可能成立.

從以上分析可知:方程(1.1)僅有解(1.2)和(1.6),滿足m>1和(3.12)式.

情況II(3.13)式成立.從(3.13)式可得

和

如果pn≡1(mod 8),則因是與pn?1互素的奇數,后者是偶數,所以從(3.30)式可得

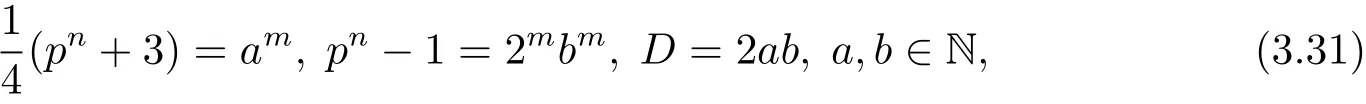
因為m>1,而且從(3.13)式可知p 6=3,所以根據引理2.9,從(3.31)式中第二個等式可得n=1,以及

再根據引理2.2,從(3.32)式可知m必為偶數.然而,此時在(3.31)式中消去pn,可得1=am?2m?2bm≥ am/2+2m/2?1bm/2>1,矛盾.

如果pn≡3(mod 4),則因與是互素的奇數,所以從(3.30)式可得

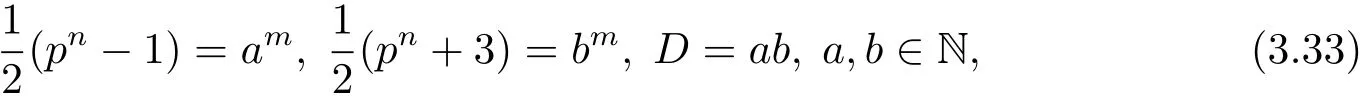
然而,因為m>1,又從(3.33)式可知b>a≥1,所以在(3.33)式中消去pn,可得

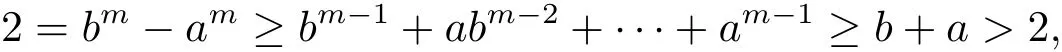
矛盾.

如果pn≡5(mod 8),則因是與pn+3互素的奇數,后者是偶數,所以從(3.30)式可得

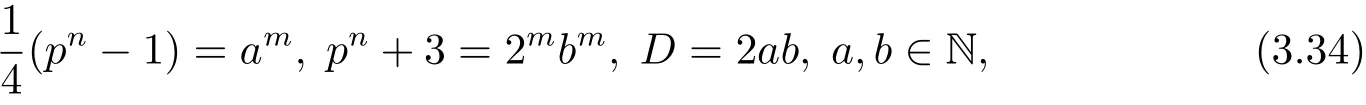
在(3.34)式中消去pn,可得

顯然,從(3.35)式可知m必為奇數.又因m>1,所以根據引理2.12,從(3.35)式可知,僅有m=3以及a=b=1.將此代入(3.28)和(3.34)式即得解(1.3).由此可知,方程(1.1)僅有解(1.3)滿足m>1以及(3.13)式.

綜合以上所有,定理證完.