擴散方程九點格式中節點未知量的一種新的插值算法

董 成,鄔吉明

(1.中國工程物理研究院研究生院,北京 100088)

(2.北京應用物理與計算數學研究所,北京 100088)

1 引言

考慮擴散方程邊值問題

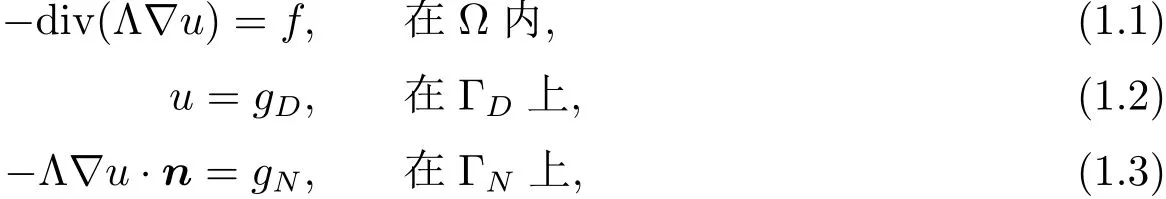
其中??R2是平面上的多邊形區域,Λ是擴散張量,f是源項,??=ˉΓD∪ˉΓN是?的邊界,n為單位外法向量,gD和gN分別是Dirichlet和Neumann邊值.

上述擴散問題有著廣泛的實際應用背景,例如在輻射流體力學、輻射磁流體力學、油藏模擬等應用中,擴散過程與其他物理過程相耦合.我們常常需要在網格強扭曲、強間斷、強各項異性、強非線性等極端條件下求解擴散方程,這是一件具有挑戰性的工作.有限體積方法是求解擴散問題最常用的方法之一,它具有局部守恒、簡單容易實現等良好性質.多年來,許多科研工作者致力于擴散方程的有限體積方法研究,提出了眾多的離散格式,如九點格式(NPS)[1]、多點通量逼近格式(MPFA)[2]、支撐算子格式[3]、廣義差分格式[4]等.按照未知量的類型,這些格式可大致分為單元中心格式、節點格式、雜交格式、混合格式等等,詳細的最新研究進展可參見文獻[5–9].

我國學者李德元教授等人在二維網格上基于積分插值法構造了一個單元中心型有限體積格式[1],由于該格式在結構四邊形網格上有九點模板,故常稱其為九點格式,它是若干輻射流體力學程序的基本格式[10,11].由于單元中心格式在一個單元上只有一個未知量,在構造離散格式時需要引入輔助未知量來提高精度.九點格式的輔助未知量定義在網格節點處,如何用單元中心未知量逼近節點輔助未知量是九點格式研究中的一個重要內容.一個理想的二維節點插值算法應當具有簡單、保正、不依賴于網格拓撲、不依賴于間斷線的位置、有二階精度、易于向三維推廣等性質.目前已知的節點插值算法,如算術平均插值[1]、逆距離加權插值[12]、最小二乘插值[13]、顯式加權算法[14]等,均只能滿足部分要求.由于缺乏容易向三維推廣的二階插值算法,嚴重制約了九點格式在三維問題中的應用.

本文在多點通量逼近的邊輔助未知量插值算法的基礎上,通過一個特殊的極限技巧獲得了一個新的節點插值算法,并在給定假設下證明了該算法中局部線性系統的可解性.本文插值算法的一個重要之處在于容易向三維推廣,且滿足除保正性以外的其他要求.全文的推導基于所謂的線性精確準則[15],即當擴散張量關于網格是分片常數、解析解關于網格是分片線性函數時,算法推導的每一步都是精確成立的.為了和通常的等式相區別,用符號’表示相關等式是在線性精確意義下成立的.

2 九點格式的構造

最初的九點格式是在擴散系數為標量的情形下推導的,但我們容易將其推廣到擴散系數為張量的情形[14],為保持本文內容的完整性,我們簡要介紹一下擴散張量情形下九點格式的一種構造算法．首先將?剖分為互不重疊的多邊形網格,K表示其中的一個單元,σ表示單元邊,K 的所有邊組成的集合記為EK,單元K 關于邊σ的單位外法向量記為nK,σ.記流向量為F=?Λ?u,這里假定Λ關于網格是分片常數,并用ΛK表示Λ在單元K 上的限制.單元K 通過邊σ的流記為FK,σ,即

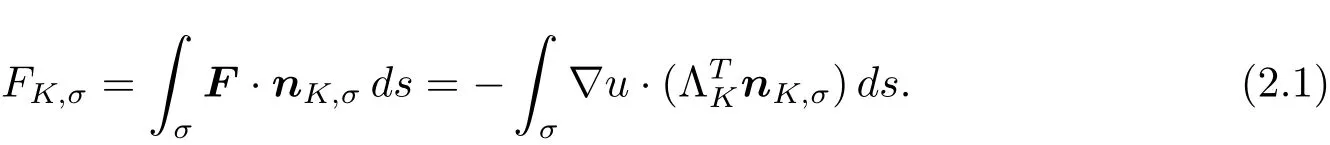
在單元K上對方程(1.1)兩端積分并利用散度定理,有

于是有限體積法解擴散問題就歸結為構造流FK,σ的離散表達式.

在圖1中,K和L表示兩個相鄰單元,它們的單元中心分別是OK和OL,σ是它們的公共邊,其頂點為A 和B,nK,σ,nL,σ分別是K,L關于σ的單位外法向量.dK,σ,dL,σ分別表示OK,OL到σ的距離,uA,uB,uK,uL表示u在點A,B,OK,OL處的近似值.對于向量v=(a,b)T,記v?=(b,?a)T.此外,為敘述簡單起見,引入以下記號(見圖1)

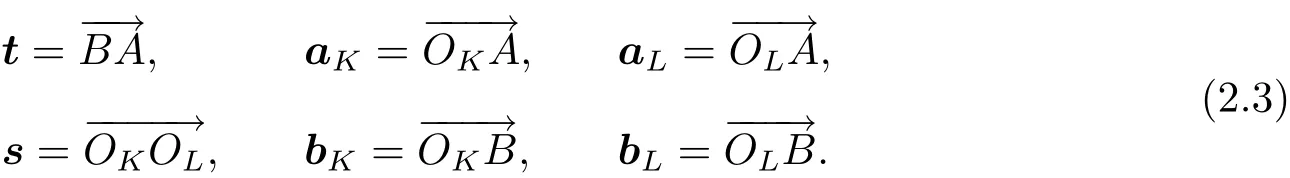
首先,有如下的向量分解

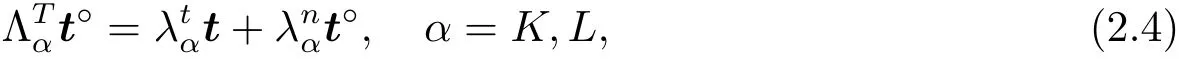
其中

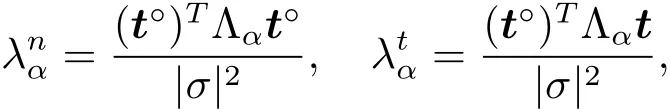
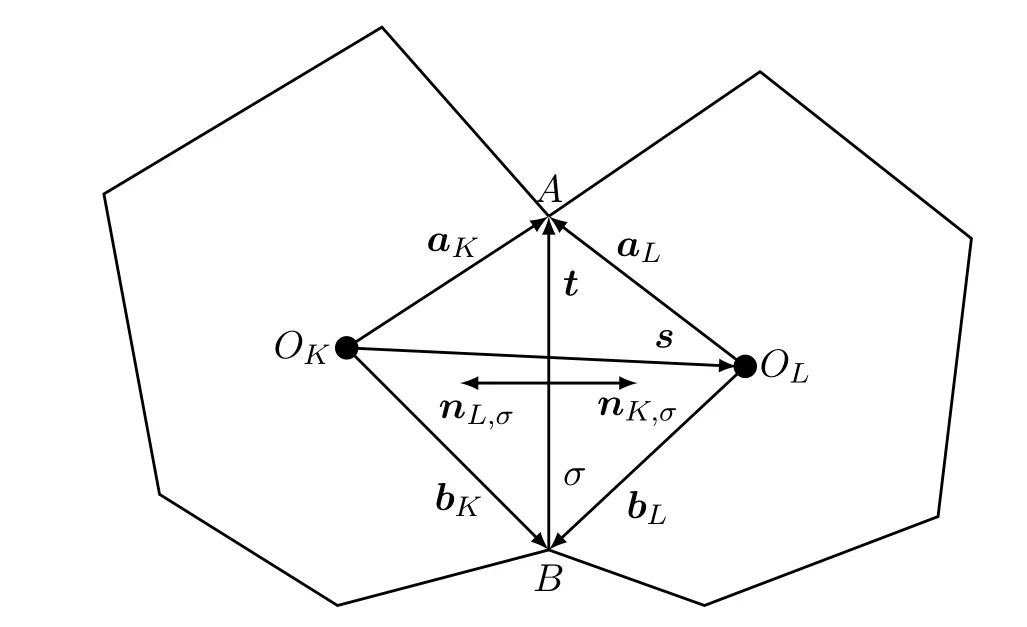
圖1:離散流構造模板

|σ|表示σ的長度.其次,在單元K 上,根據文獻[14]的引理2.1,

注意到 |σ|nK,σ=t?,t=aK? bK,·t= ?|σ|dK,σ,將 (2.4) 和 (2.5) 式代入 (2.1) 式,經過簡單的計算后就可以得到

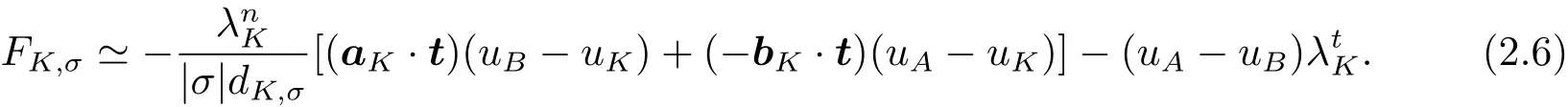
類似地,在單元L上,有

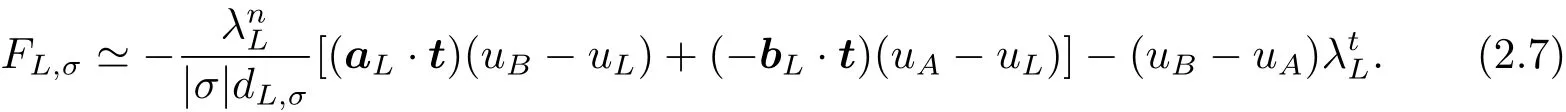
通常要求通過邊σ的流滿足連續條件,即

由此得到

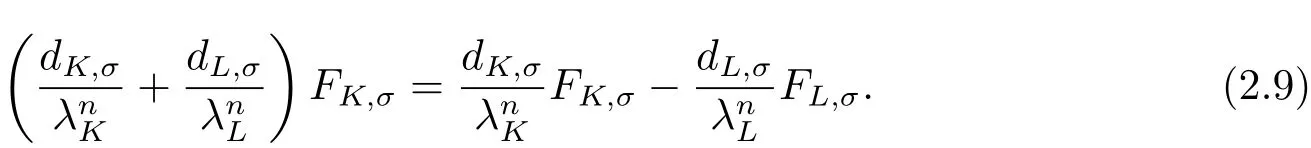
將(2.6)和(2.7)式代入(2.9)式的右端,利用aK?bK=aL?bL=t,aK?aL=bK?bL=s,并經過簡單化簡就得到內部邊σ上流的離散表達式

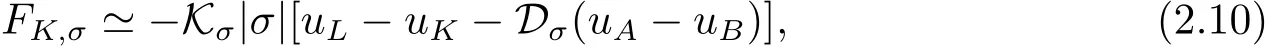
其中

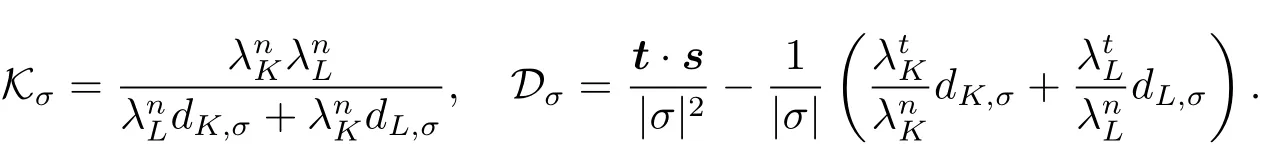
容易看出,上述離散流涉及單元中心未知量uK和uL以及節點輔助未知量uA和uB,要得到純單元中心格式,需要用單元中心量對節點輔助未知量進行插值.

3 節點輔助未知量的插值算法

如圖2(a),假設Q0是一內部節點,它周圍的單元?k(1≤k≤n)按逆時針順序排列.Q0Pk和Q0Pk+1是?k的以Q0為頂點的邊,Ok為其中心.假設Tk是邊Q0Pk上的一點,由下式確定

其中τ∈(0,1).令u0,uk,分別表示Q0,Ok,Tk處的未知量,Λk表示Λ在?k上所取的分片常數值,nk表示?k關于Q0Pk的單位外法向,見圖2(b).本文中k將被視為以n為周期的指標,例如當k=n+1和0時,有Pn+1=P1,T0=Tn.

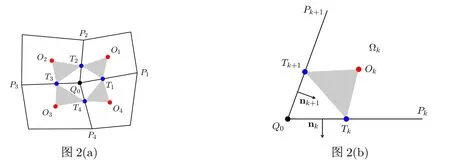
圖2:內部節點Q0處的局部結構和記號

3.1 邊輔助未知量的插值算法

在多點通量逼近格式中,邊未知量ˉuk可以通過單元中心未知量uk表示.為敘述簡潔起見,引入以下記號

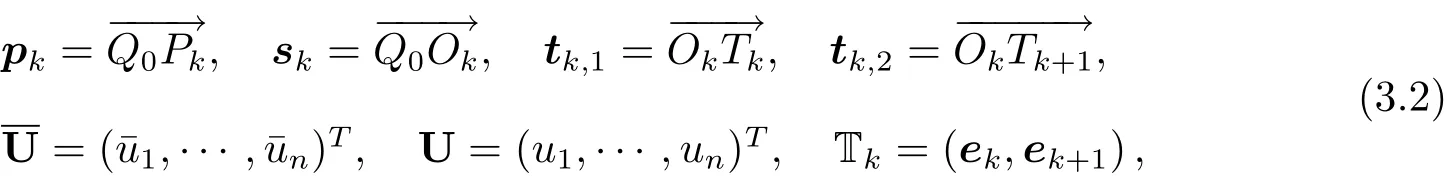
其中ek表示n階單位矩陣的第k個列向量.顯然,Tk是一個n×2的矩陣,并且

在單元?k的邊Q0Pk和Q0Pk+1上,定義如下離散流

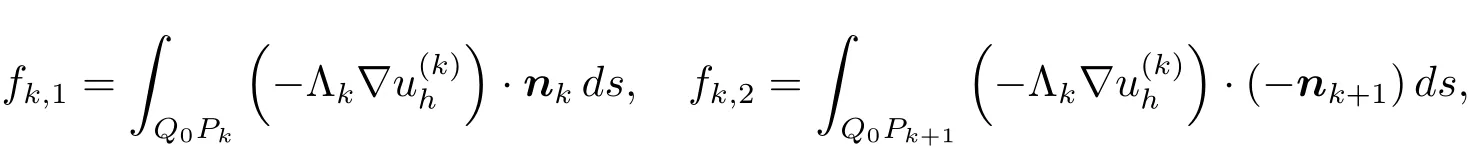
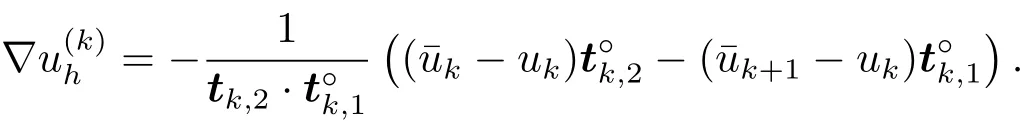
注意到對于 Q0Pk(Q0Pk+1),有于是

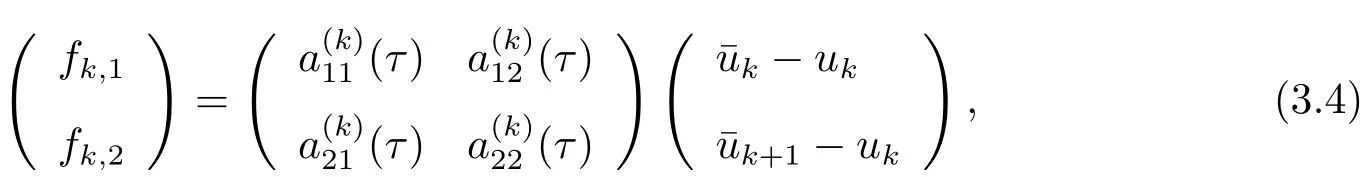
其中

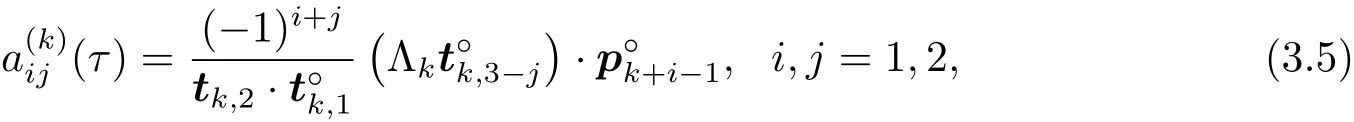
這里記號(τ)表示相關的量是τ的函數,在不引起歧義的情況下將其省略.利用(3.3)式,可將(3.4)式改寫為

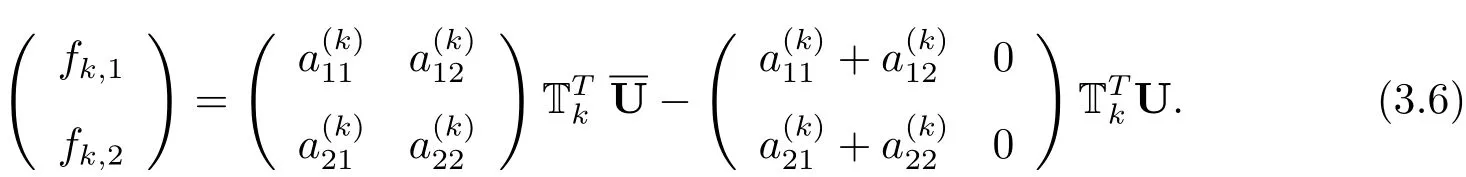
再利用邊Q0Pk+1上的流連續條件,即

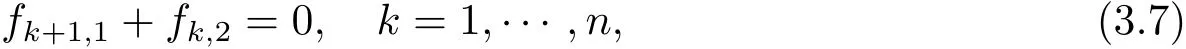
或者其等價形式

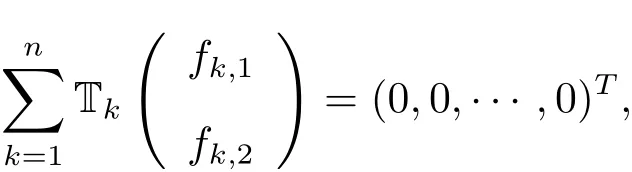
就得到

其中

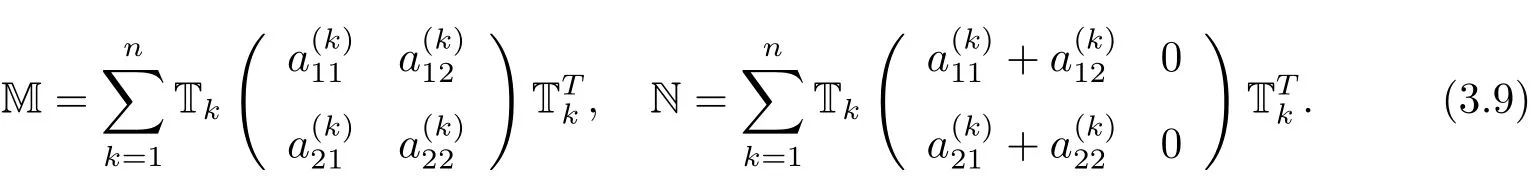
通過求解(3.8)式,就能夠用單元中心未知量來表示邊未知量,即=M?1NU.容易看出,只有當M可逆時,上述邊未知量插值算法才是可行的.自多點通量逼近算法提出來的二十多年里,人們還沒有在數值計算中遇到過M奇異的情形,但這一點至今仍缺乏嚴格的理論證明.

3.2 新的節點未知量插值算法

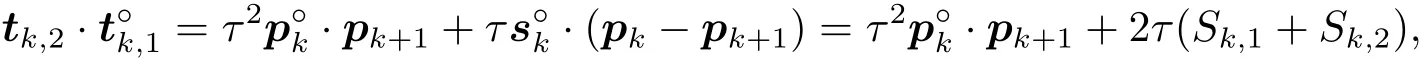
其中Sk,1(Sk,2)表示4Q0PkOk(4Q0OkPk+1)的面積.于是(3.5)式可以寫為

其中

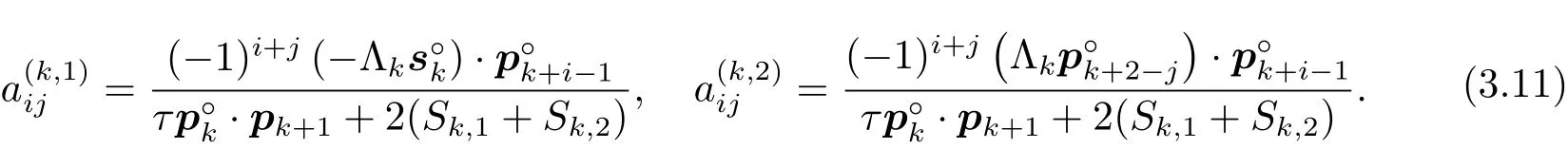
再利用(3.9)式,可得

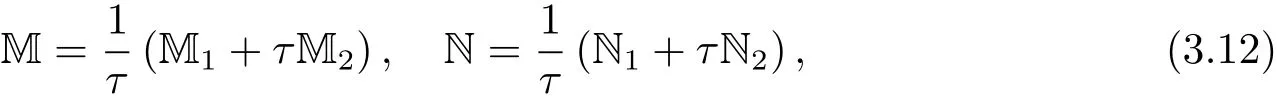
其中

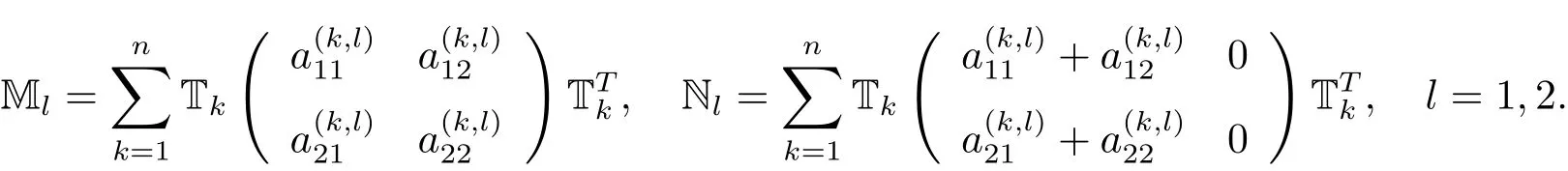
需要注意,由于(3.11)式的分母中含有τ,Ml和Nl依然是τ的函數.根據(3.11)式,發現

故有

其中1和0分別表示所有分量為1和0的向量,O表示零矩陣.利用(3.12)和(3.14)式,可證(3.8)式等價于

注意到解沿著Q0Pk(1≤k≤n)是切向連續可微的,通過泰勒展開,可以得到

其中 Γ =(γ1,···,γn)T是與 τ無關的常向量,O(τ2)表示所有分量為 O(τ2)的向量. 將(3.16)式代入(3.15)式并且利用(3.14)式中的第一個等式,得到

最后將以上方程兩端同時除以τ,并令τ→0,就得到最終的方程

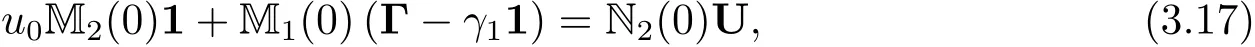
其中M1(0),M2(0)和N2(0)表示M1,M2和N2取τ=0的值.將M1(0)的第一列替換為M2(0)1其余列不變得到一個新的矩陣,記為,則(3.17)式可以寫為與τ無關的線性系統

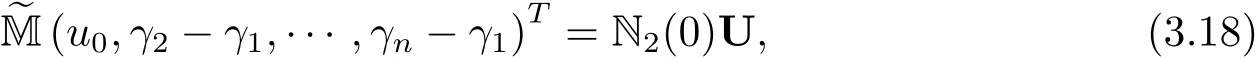
求解上述局部線性系統就得到一個新的節點插值算法,即

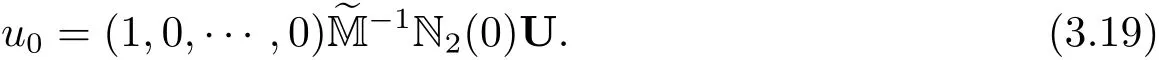
這里需要特別強調,雖然上述算法基于多點通量逼近的邊輔助未知量插值,但它與(3.8)式中矩陣M的可逆性沒有關系.

4 局部線性系統(3.18)的可解性

雖然(3.8)式的可解性目前尚無理論證明,但局部線性系統(3.18)式的可解性在一定條件下是可以嚴格證明的.本節的主要結果依賴以下兩個假設:

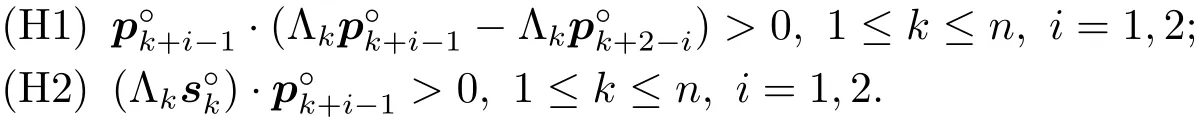
在擴散系數是標量的情況下,假設(H1)和(H2)的幾何意義是明顯的,此時,兩個假設變為

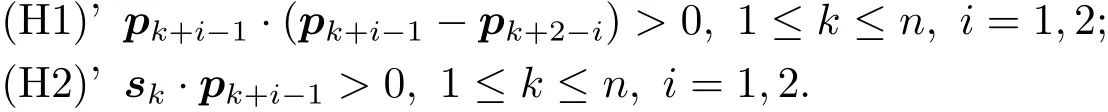
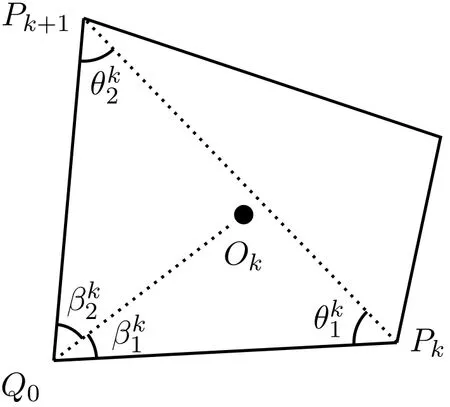
圖3:假設(H1)和(H2)的幾何意義

引理4.1在假設(H1)下,M2(0)1的所有元素都是負的,即

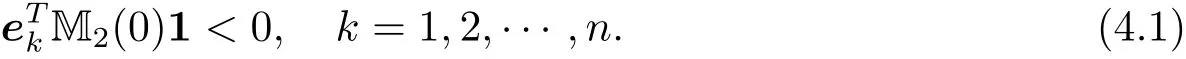
證 由M2(0)的定義,有

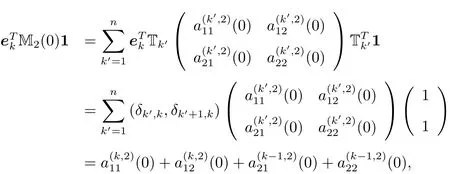
其中δij表示Kronecker delta函數.利用(3.11)式并且注意到τ=0,進一步得到

再結合假設(H1),立即得到(4.1)式.

引理4.2記A=(aij)為n×n的矩陣,滿足

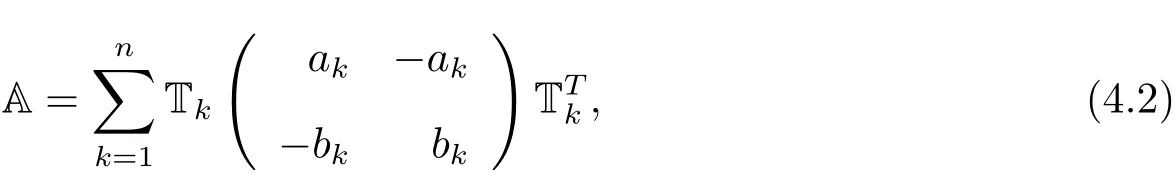
其中ak,bk(1≤k≤n)是正數.則

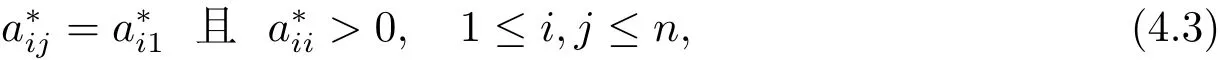
證 根據(4.2)式,有

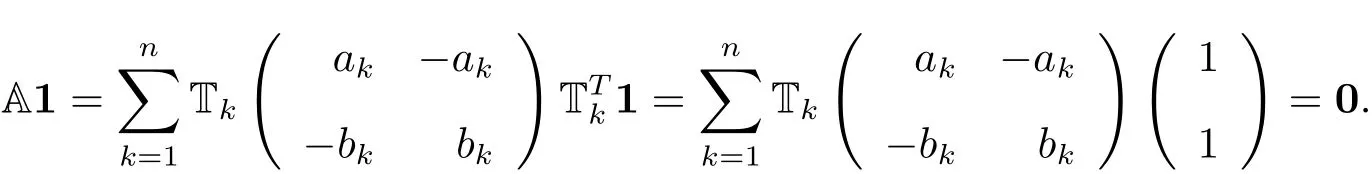
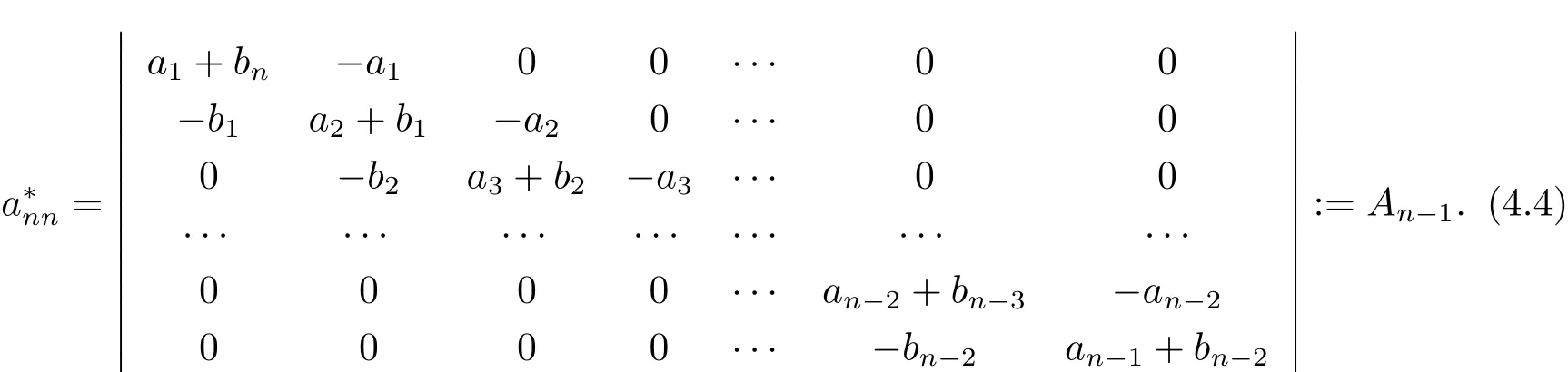
分裂An?1的最后一列,可得

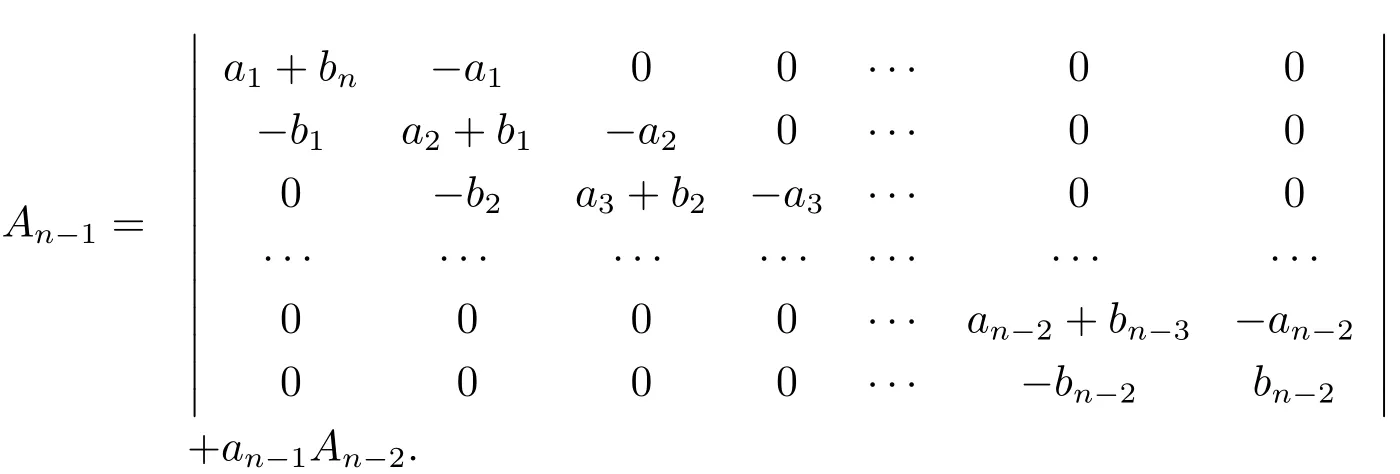
對于An?1的第一部分,通過將最后一列加到第(n?2)列,再將新的第(n?2)列加到第(n?3)列,依此類推,最終可得到一個上三角型行列式,進而有

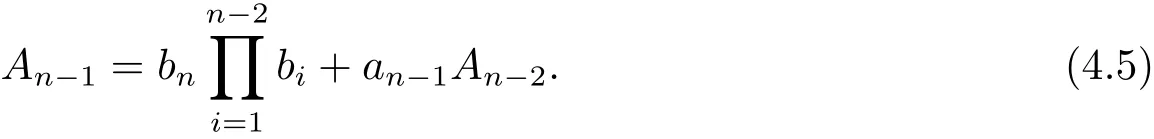
用同樣的方法可以得到

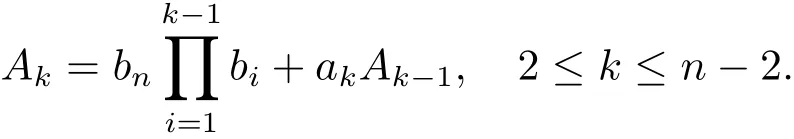
注意到A1=a1+bn>0以及ai,bi>0,通過數學歸納法最終得到An?1>0,從而>0.類似地,可以證明>0.當i 6=1,n時,記aii對應的余子式為,并令

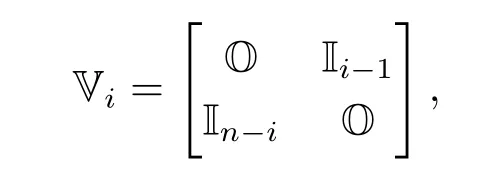
其中Ik是k階單位矩陣.容易驗證是形如(4.4)式的三對角矩陣.于是

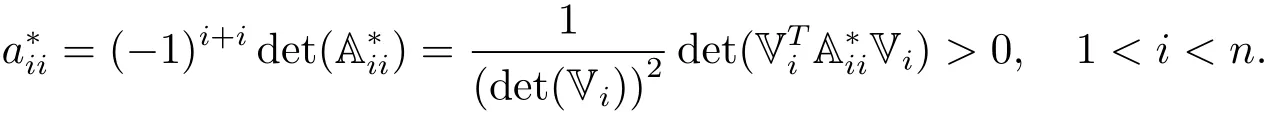
定理4.3 在假設(H1)和(H2)的條件下,(3.18)式中的系數矩陣 eM是非奇異的.

證 由M1(0)的定義和(3.13)式,有

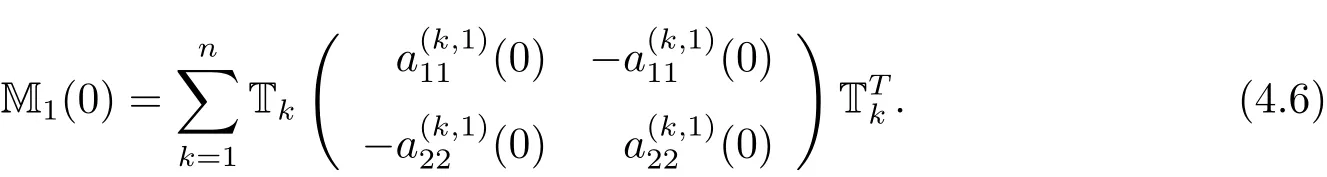
由(3.11)式和假設(H2),可以得到

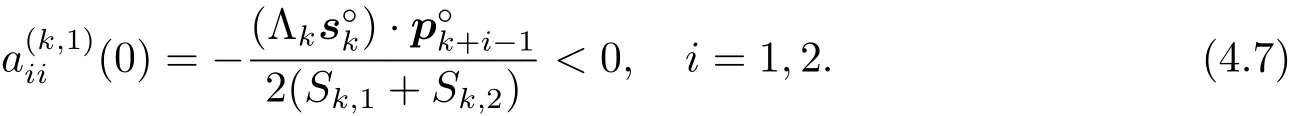
令A=(aij)n×n= ?M1(0).根據引理4.2,>0(1≤k≤n).由 eM 的定義,并利用引理4.1,可得

5 數值實驗

首先,定義如下的L2誤差和流誤差

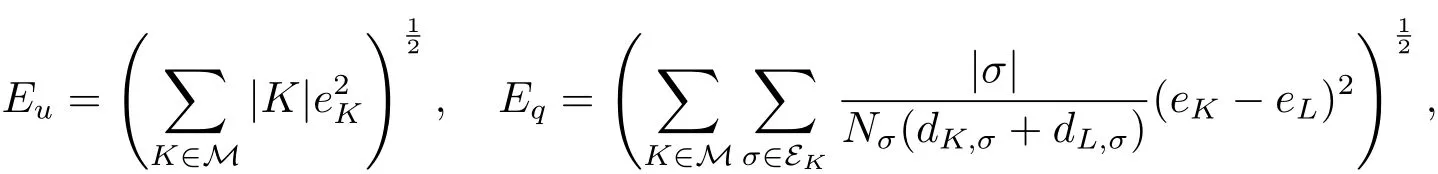
其中M為單元集合,eK表示單元K中心的誤差,Nσ表示邊σ的相鄰單元數,L表示σ的除K 之外的另一相鄰單元（如果存在的話）,當σ在邊界上時,我們約定dL,σ=eL=0.兩個網格層之間的收斂率Rα(α=u,q)通過以下公式獲得

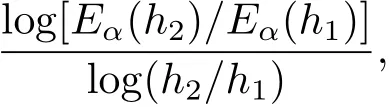
其中h1,h2代表兩個網格層的網格尺寸,Eα(h1),Eα(h2)為對應的離散誤差.

用BICGSTAB方法求解離散線性系統,并取收斂準則為εlin=1.0E-15.離散流采用公式(2.10),節點插值算法分別采用文獻[14]中的顯式加權算法2和本文的極限加權算法,對應的格式簡記為NPS-EW2和NPS-LW.采用的計算網格見圖4,且所有的計算均在雙精度下完成.

圖4:計算網格

5.1 實驗1:各向異性問題

考慮?=[0,1]2上的具有全Dirichlet邊界的擴散問題(1.1).擴散張量和精確解如下

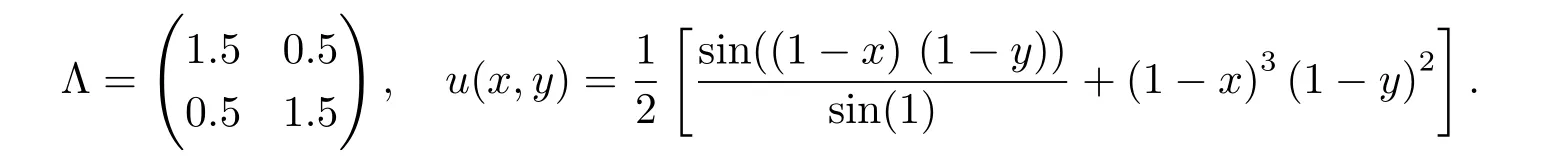
這個數值實驗是文獻[5]中的一個測試的一個簡單變形.

從實驗結果來看,NPS-LW在各網格上與NPS-EW2的實驗結果接近,這里僅給出前者的計算結果.表1給出了NPS-LW在各個網格上數值解和流的誤差,圖5以對數折線圖的形式展示了收斂速度.可以看出NPS-LW在這些網格上的數值解的誤差隨著網格加密以趨近2階的速度收斂.

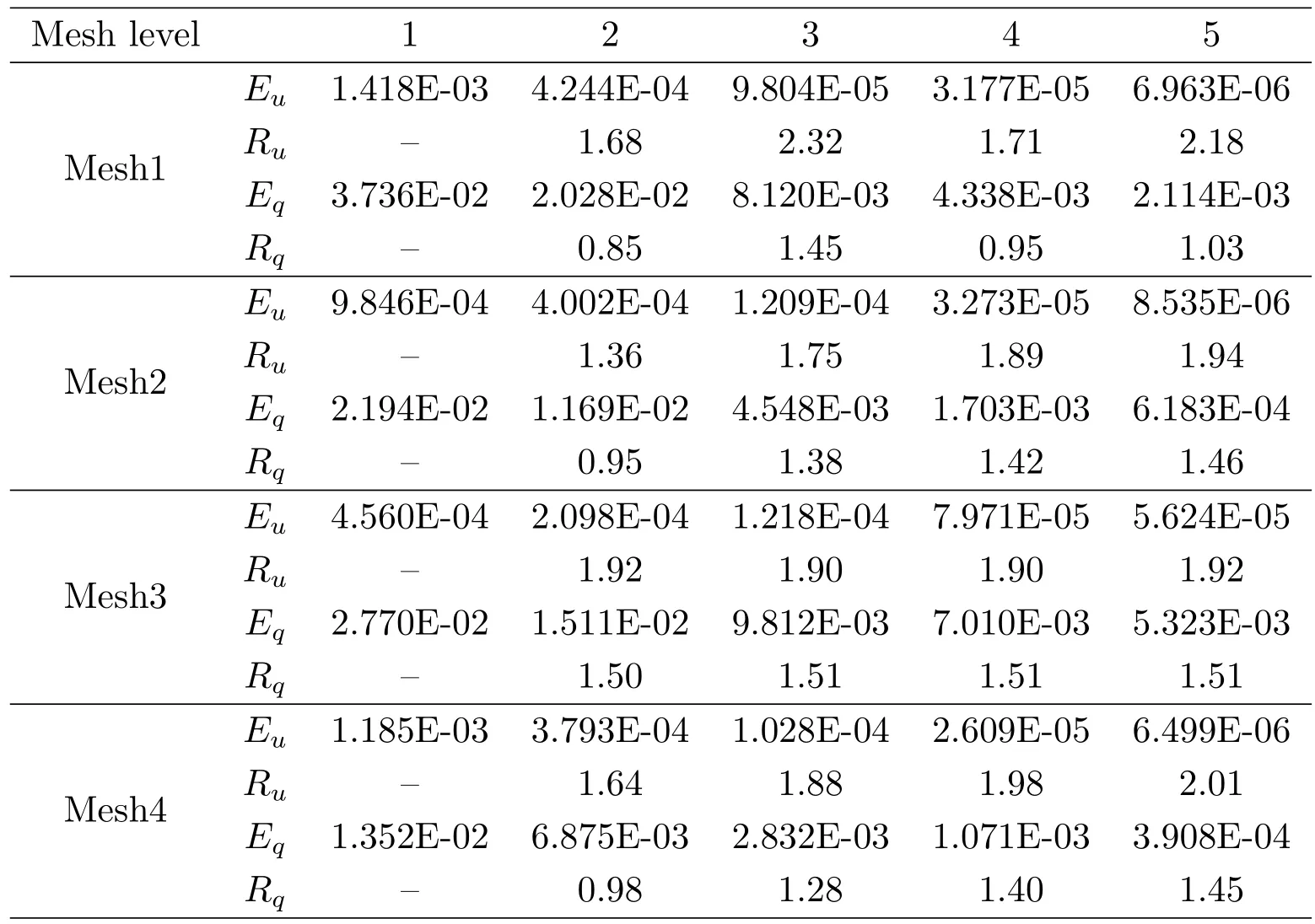
表1:NPS-LW在實驗1中的數值結果

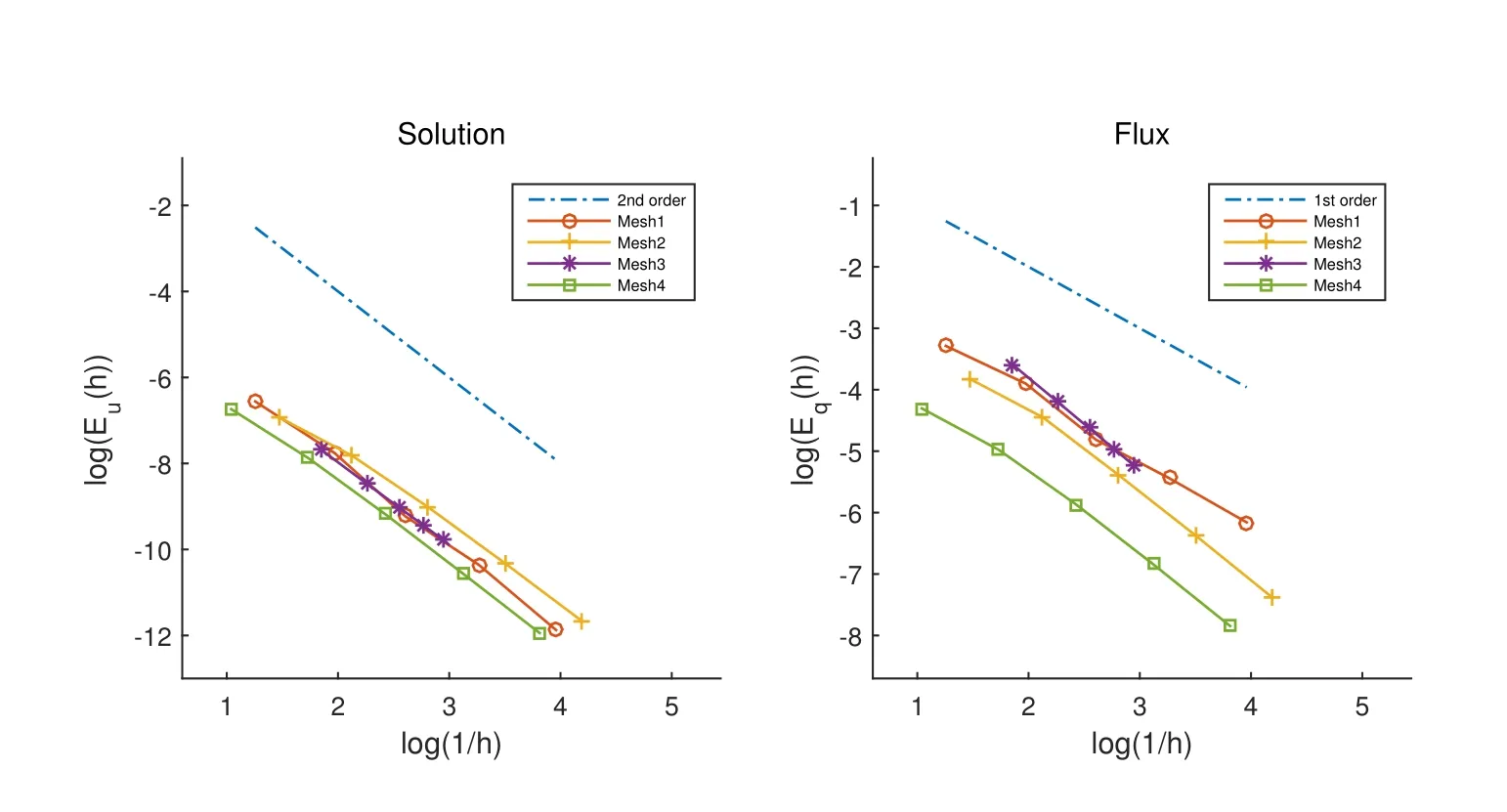
圖5:NPS-LW在實驗1中的誤差曲線

5.2 實驗2:泊松問題

在[0,1]2上求解泊松方程??u=4.0,采用Dirichlet邊界條件,解析解取為

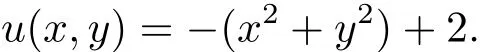
本算例十分簡單,其設計目的是測試新的節點加權算法與已有顯式加權算法在數值表現上的差異.NPS-LW的數值結果在Mesh1,Mesh2和Mesh4上與NPS-EW2非常接近,但在Mesh3上明顯優于NPS-EW2,在表2中進行了對比.

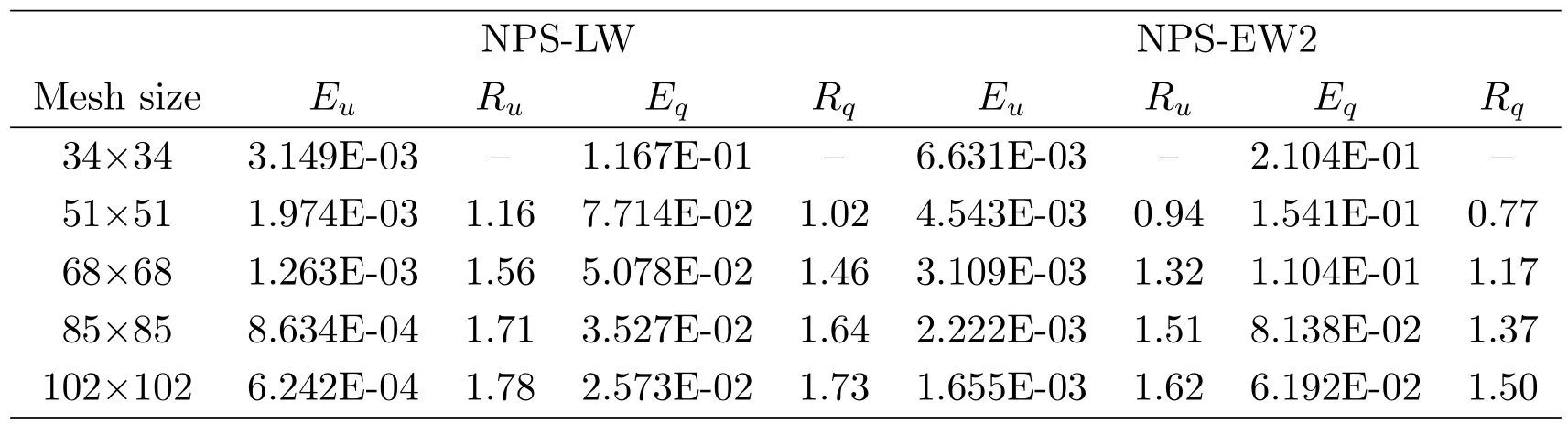
表2:NPS-LW與NPS-EW2在Mesh3上的數值結果對比

5.3 實驗3:間斷系數問題

在?=[0,1]2上求解擴散問題(1.1)–(1.2),擴散張量取為

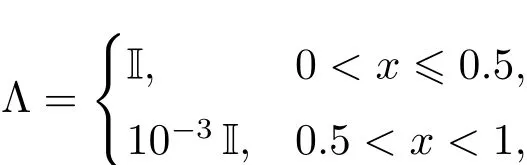
I為二階單位矩陣,精確解取為

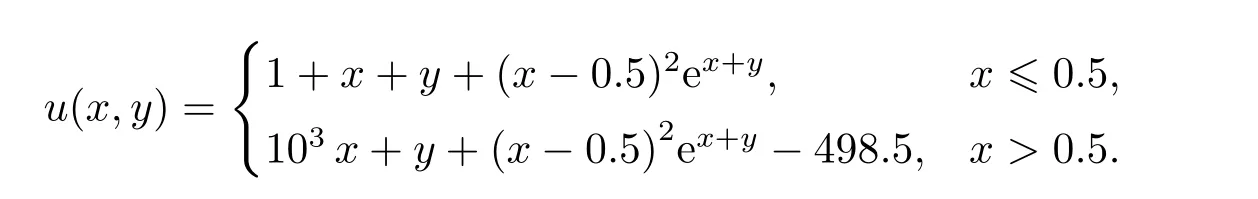
這里采用Mesh1和Mesh4.對于Mesh1,所有位于x=0.5上的節點在x方向上都不擾動.數值計算結果見表3.從該表中可以看到,數值解誤差收斂速度均趨于2階,流的誤差接近1階,均為最優階,表明新的節點加權算法也能很好地適應間斷系數問題.

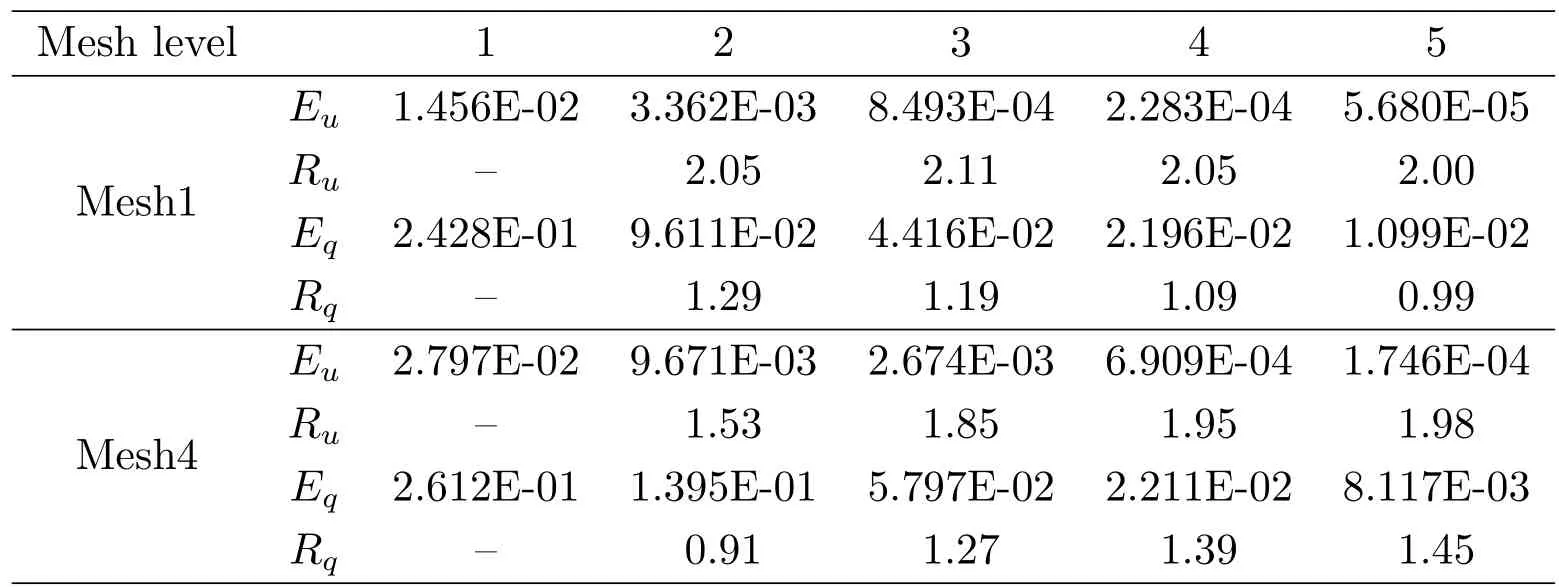
表3:實驗3 NPS-LW在Mesh1,4上的數值結果