量子微波制備方法與實驗研究進展*

苗強 李響 吳德偉 羅均文 魏天麗 朱浩男

(空軍工程大學信息與導航學院, 西安 710077)

1 引 言

量子信息科學建立在量子力學的疊加性、糾纏性、非局域性和不可克隆性等特性的基礎上, 可以突破現代經典信息技術量測的物理極限, 開拓了與經典電磁應用方式具有本質區別的全新信息處理功能[1]. 目前正在研究利用的基于空間傳播場的量子信息技術主要包括量子通信、量子定位、量子雷達等[2?4]. 由于高能單光子在光子探測等實際應用中具有優勢, 使得光學波段量子信息技術的研究與應用在當前量子信息技術發展進程中占據主導地位. 然而, 光波的自由空間傳輸受天氣條件及大氣塵埃、粒子影響較大. 相對于可見光及其他頻段電磁信號, 微波受大氣環境影響較小, 云霧穿透能力較強, 而且在高功率信號產生以及接收探測等方面具有一定的優勢, 現行很多基于自由空間傳播場的信息傳輸系統工作于微波波段.

近年來, 科研工作者們已通過多種不同方式在實驗中發現或制備了微波頻段的非經典電磁場–量子微波, 如微波單光子、微波糾纏光子對、壓縮態微波場和糾纏態微波場等. 量子微波信號既保留了經典微波信號在空間中的遠距離傳播能力, 又具有非經典的量子特性, 在大尺度動態空間環境中具有重要的應用前景, 甚至會對傳統的通信、導航、雷達等領域產生顛覆性影響. 量子微波的生成為微波頻段量子信息處理、量子隱形傳態、量子密集編碼, 特別是微波量子通信、微波量子雷達以及量子超精密測量等基于空間傳輸的量子信息技術提供了可資利用的重要信號源. 作者及其研究團隊近年來持續跟蹤量子微波相關實驗進展, 對目前產生非經典微波的原理、方法及其相關典型實驗進行了歸納分析, 并探討了非經典微波在量子導航等自由空間傳輸系統應用中需著重破解的若干關鍵問題.

2 腔量子電動力學系統、超導電路量子電動力學系統和腔–光(電) –力學系統

腔量子電動力學系統(cavity quantum electrodynamics, C?QED)與超導電路量子電動力學系統 (circuit quantum electrodynamics, c?QED)是實現量子微波的兩類最重要的實驗平臺. 此外,近年來研究較多的腔–光(電)–力學系統也被用來產生非經典微波. 目前的量子微波制備主要基于以上三類系統實現各種不同類型的非經典、非線性量子效應, 如克爾效應(Kerr effect)、卡西米爾效應(Casimir effect)、三波混頻 (three?wave mixing)、四波混頻(four?wave mixing)等, 以產生不同性質的量子微波.

腔量子電動力學系統描述了在高品質的共振腔中某一物質(一般為原子、分子系統)與電磁場之間的相干耦合. 在強耦合情況下, 原子在從腔場泄露出來之前, 與單模腔場多次發生單光子交換.而通過腔場與雙能級原子(或分子及其他系統)的相互作用可以產生腔場的非經典態[5?7].

超導電路量子電動力學系統是基于超導傳輸線和超導約瑟夫森結(Josephson junction)耦合構成的超導微電路, 它可以看成是原子腔量子電動力學原理在固態領域的實現. 基于超導約瑟夫森結的量子比特(qubit)對應人工原子, 與之耦合的超導傳輸線對應光學微腔[8,9]. 根據約瑟夫森能(energy of Josephson)和充電能(energy of charge)的大小, 可以將量子比特分為電荷量子比特(charge qubit)、磁通量子比特(flux qubit)、相位量子比特(phase qubit)以及傳輸子量子比特(transmon qubit)等. 超導電路量子電動力學系統的典型工作頻率范圍在1–10 GHz. 與腔量子電動力學系統相似, 超導電路量子電動力學系統也可以產生微波頻段的非經典態, 而且微波光子可以在超導傳輸線中無損傳輸, 具備良好的量子相干性和可集成性, 是目前最受重視的固態量子信息處理系統之一[10?13].

腔–光–力學系統(cavity optomechanical system)是光腔與機械振子相結合的系統, 其典型結構是光場被增強的光學共振腔(或者微腔), 其一端帶有可移動的反射鏡或等效為腔鏡的各種結構(機械振子), 如圖1(a)所示. 在腔–光–力學系統中,光與機械諧振子的非線性相互作用導致了很多非經典的效應, 如類電磁誘導透明現象、腔場與機械振子之間的糾纏以及場的非線性, 因此使得這一體系成為重要的量子系統[14,15].

圖1 (a) 腔–光–力學系統結構示意圖; (b) 腔–電–力學系統結構示意圖Fig. 1. (a) Schematics of the cavity optomechanical system;(b) schematics of the cavity electromechanics system.

腔–電–力學系統 (cavity electromechanics system)是腔–光–力學原理在微波頻段的實現, 結構很相似. 它由微波腔和機械振子結合, 如圖1(b)所示. 微波腔由LC振蕩電路構成, 電容器的一端固定, 另一端可移動, 當腔體受到微波場驅動作用時, LC振蕩電路中的電流發生變化, 使得電容器移動端的位置和體系電容發生改變的同時引起回路中的電流再次變化, 導致微波場與機械振子發生相互作用[16].

3 量子微波制備方法與典型實驗進展

在探討量子微波源之前, 有必要區別一下“微波光子”一詞的兩個概念. 在常見的微波工程或光學工程論著里, 微波光子學是研究微波和光波相互作用規律及應用的一門新興學科, 用光子學的方法來產生、分配、處理微波信號, 根本目標是提升現有的微波系統的性能, 使得系統在頻率、帶寬、動態范圍、抗干擾等方面獲得提升[17], 而這并不是本文涉及的“微波光子”. 本文所研究的“微波光子”是微波頻段的電磁場能量量子, 是微波場的基本能量單元, 是光頻光子在微波頻段的對應[18].

量子信息科學根據所利用的量子系統的本征態具有分離譜或是連續譜結構, 將量子變量分為分離變量與連續變量兩大類[19,20]. 能夠用有限維希爾伯特空間表征的量子變量為分離變量, 如光子或光場的偏振. 另一類量子變量, 如粒子的位置與動量、光場的正交振幅與正交位相分量等, 它們的每一個值對應不同的正交本征態, 其本征態構成無限維希爾伯特空間, 稱為連續變量. 以下分別探討微波頻段的分離變量量子系統(微波單光子和糾纏微波光子)和連續變量量子系統(壓縮態微波場和糾纏態微波場)的產生方法、原理和實驗進展.

3.1 微波單光子的制備

產生單光子是制備光子偏振態、光子數態(Fock態)的基礎. 在光學頻段, 單光子的產生可以有多種途徑[21], 如激光衰減方法、腔量子電動力學方法(單個原子或分子、量子點單光子源)、自發參量下轉換(spontaneous parametric down?conversion,SPDC)等. 可以類比光頻單光子源研究產生微波單光子, 但由于頻率相差幾個數量級, 因此微波光子比光頻光子能量微弱很多. 波長的紅外光子等效溫度為10000 K, 而波長3 cm的微波光子等效溫度僅有0.5 K, 因此常溫環境下極難觀測、驗證微波場的量子效應[22]. 近年來在微波單光子源及探測器研究方面取得了較大進展. 按照實驗途徑, 目前研究較多的微波單光子制備方法可基本劃分為腔量子電動力學和超導電路量子電動力學方案.

3.1.1 腔量子電動力學系統

單原子或者一些類原子系統在電學激發下能發射出單個光子. 處于激發態的電子通過自發輻射躍遷到基態后產生一個光子. 由于躍遷需要一定的時間, 處于激發態的原子在輻射光子并返回基態前不會吸收光子, 所以原子(或類原子)系統產生的光子是嚴格的單光子. 腔量子電動力學系統為實現這種產生方法提供了原子系統與場相互作用的平臺–微波諧振腔, 即利用微波腔中的原子系統與電磁場的相互作用產生微波單光子輻射.

腔量子電動力學方法制備微波單光子的典型代表是微–微波激射器(micro?maser)或單原子微波激射器. 微波激射器是含有一個微波腔和一束入射到腔中的處于激發態原子流的物理系統, 原子流足夠稀疏以至每次最多只有一個原子出現在微腔中. 微波激射器為觀察原子與輻射場相互作用的量子特性提供了最簡單的物理系統[23]. 利用微–微波激射器已可以實現多種量子效應, 如微波場的亞泊松分布、光子數態[24]和壓縮態[25]的產生等.

圖2 腔量子電動力學系統Fig. 2. Cavity quantum electrodynamics system.

張智明教授團隊對微–微波激射器作為腔量子電動力學系統進行了廣泛而深入的研究, 如圖2所示. 設有一個兩能級原子, 其基態為, 激發態為. 初始時, 原子由態進入真空態為的腔中,腔模頻率等于躍遷頻率, 初始的原子–腔態表示為. 當原子躍遷到基態時, 腔中產生一個光子, 此時原子–腔態表示為[26]. 通過控制進入微–微波激射器腔中的原子(或分子)數, 能夠達到輻射單光子的目的. 為了觀測到理論所預言的量子效應, 首先原子通量要足夠小,以保證在任何時刻, 腔中最多只有一個原子, 從而實現單個原子與電磁場的相互作用. 另外原子與腔場的相互作用需要足夠強. 處于高里德堡(Rydberg)態的原子可以滿足這一要求, 而且相鄰里德伯態之間的躍遷頻率正好處在微波區(10–120 GHz). 實驗所用處于里德伯態的銣原子, 其能級63P3/2與61D3/2之間的躍遷頻率約為21.5 GHz[27,28].Jones團隊利用微–微波激射器對微波光子進行級聯放大, 在微腔中激發態里德堡原子與腔場光子相互作用, 通過微腔出射原子的里德堡狀態實現微波單光子的探測. 實驗中的微–微波激射器使用處于里德堡態63P3/2的激發態銣原子, 基態為61D5/2,躍遷頻率21.456 GHz[29].

除單原子或分子外, 量子點方法在光頻單光子制備和探測方面研究較多, 但尚未見到利用量子點產生微波單光子的相關實驗. 但只要設計合適的材料制備半導體量子點使其二能級差處于微波頻段,理論上也可實現微波單光子輻射.

3.1.2 超導電路量子電動力學系統

由于超導量子比特包含很多原子, 其有效偶極矩(dipole matrix)比堿金屬原子和里德伯原子大很多, 而且一維傳輸線模體積小, 因此即使固態環境的干擾作用較強, 超導電路與腔的強耦合仍然是可以實現的, 能夠觀察到單個人工原子和單個微波光子的相互作用[30,31]. 基于超導電路量子電動力學系統, 近年來的研究取得了一系列重要進展, 例如,觀察到了微波光子的類粒子特性, 實現了微波單光子態和光子數態的制備和檢測[32?34].

Bozyigit等[35]和Eichler等[36]利用超導電路實現了微波頻段單光子態產生與檢測技術的新突破, 如圖3所示. 他們用精確操控的超導量子比特與諧振腔的耦合電路實現了微波單光子源, 其多光子的發射概率基本可以忽略.

圖3 微波單光子產生設備[35], 左側內插圖為超導量子比特 a： 超導傳輸線諧振腔; c： 輸出電容; d： 熱噪聲端口;e/f： 相干測量端口; Z0 和 Z1 為匹配阻抗Fig. 3. The experimental set?up of generating microwave single?photon, where the left inset denotes qubit. a： super?conducting transmission line resonator; c： output capacit?ance; d： thermal noise port; e/f： coherent measurement port; Z0 and Z1 are matching impedance.

2016年, Peng等[37]利用片裝可控超導人工原子(量子比特)與兩端開路傳輸線(控制和輻射傳輸線)的非對稱耦合電路實現了可控的微波單光子源, 如圖4所示. 該單光子源中的人工原子與控制傳輸線弱耦合, 而與輻射傳輸線強耦合, 人工原子經微波脈沖激勵后在傳輸線中輻射微波單光子,該實驗在7.75–10.5 GHz的可調頻域內得到近90%的單光子效率, 光子頻率的調整由外加磁通控制. 在探測方面, Yin等[38]利用電流偏置的約瑟夫森結作為一個三能級系統實現了微波單光子的探測, 探測效率達到70%. 該約瑟夫森結可以從入射場中吸收微波單光子, 并用于工作在4 GHz的HBT(Hanbury?Brown and Twiss)實驗驗證微波熱態的光子群聚效應. 日本Tokyo Medical and Dental University的Kunihiro等[39]和Inomata等[40]利用超導量子比特的綴飾態構成的人工Λ系統實現微波單光子探測. 微波單光子引起Λ系統的拉曼躍遷(Raman transition)并激發量子比特, 從而實現微波單光子探測, 其單光子探測效率達到66%.

圖4 頻率可調微波單光子源原理與結構[37]Fig. 4. Principle and structure of frequency?adjustable mi?crowave single?photon source.

利用超導電路量子電動力學實現單光子探測是目前研究最為廣泛和深入的方法. 除此之外, 利用其他物理效應探測微波單光子的方法也不斷被提出, 如微波動態電感探測器(microwave kinetic inductance detector, MKID)、超導轉變邊界光子探測器(transition edge sensors, TESs)、超導隧道結 (superconducting tunnel junctions, STJs)、超導納米線(superconducting nanowire single photon detector, SNSPD)等[41].

3.1.3 腔–光 (電)–力學系統

利用腔–光(電)–力學系統實現微波單光子源的實驗未見報道. 目前只有通過電–光–力學系統(electro?opto?mechanical, EOM)實現微波光子和光頻光子的路徑糾纏來間接產生微波單光子的方案. 即： 若在一路探測到光頻單光子, 則在另一路必定獲得微波單光子, 相關內容在后續糾纏微波光子制備部分探討.

3.2 糾纏微波光子的制備

糾纏微波光子對或多組分糾纏微波光子可用于微波頻段量子通信或量子雷達, 成為微波頻段重要的量子信息源. 光頻量子糾纏源的制備研究較為深入, 其產生糾纏光子的主要物理機理包括： 基于二階非線性效應的BBO, KDP等晶體或者PPLN,PPKTP等準相位匹配晶體的自發參量下轉換; 基于三階非線性效應的色散位移光纖或者光子晶體光纖中的四波混頻過程等. 糾纏微波光子的產生方法可參照糾纏光子的制備原理, 關鍵在于制備類似產生光頻糾纏光子的BBO, PPKTP等晶體的非線性器件或系統.

目前已有多種制備糾纏微波光子的理論和實驗研究方法, 實現的物理機理也與光頻糾纏光子制備相似, 主要是利用腔量子電動力學系統、超導電路量子電動力學系統以及腔–光(電)–力學系統等幾類系統實現類似糾纏光子生成過程的非線性效應.

3.2.1 腔量子電動力學系統

腔量子電動力學系統產生光頻糾纏光子的基本原理是利用原子與高品質因數值光腔的耦合作用, 已有多種方案提出并進行了實驗驗證[42?44]. 而利用腔量子電動力學系統產生糾纏微波光子的關鍵問題在于能級差處于微波頻段的材料. 腔量子電動力學系統中實現糾纏微波光子對的典型途徑是超導納米結構–量子點(對應光頻的原子). 量子點導帶和價帶的帶間躍遷可以產生可見光頻段光子,而帶內躍遷則可產生微波頻段光子. Emary和Trauzettel[45]利用一對量子點的帶內躍遷產生了偏振糾纏的微波光子對, 如圖5所示. 四個量子點置于圓柱形微波諧振腔中, 兩個量子點(L,R)提供電子的初態和終態, 另外兩個量子點(A,B)提供衰變路徑. 電子從L中的高能級初態隧穿進入(A,B)的高能級的疊加態, 然后通過輻射兩個光子衰變到基態. 量子點A(B)中產生兩個左旋CP+(或右旋CP?)的圓偏振光子, 即量子點與微波光子系統的態為

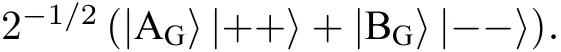
通過量子點(A,B)與量子點R耦合, 使微波光子對與電子解糾纏, 得到糾纏微波光子對中的參量下轉換產生光頻糾纏光子對的物理機理.

圖5 利用量子點產生糾纏微波光子對的原理[45]Fig. 5. Principle of generating entangled microwave photon pair using quantum dots.

Shi等[46]提出了利用HgTe量子點產生偏振糾纏光子, 輻射光子在太赫茲范圍(MeV量級), 并從理論上論證了該方案對量子點內無序性的魯棒特性, 但目前尚未見到相關實驗報道.

3.2.2 超導電路量子電動力學系統

超導電路量子電動力學系統是目前產生微波糾纏光子對的重要平臺. 利用不同結構的超導電路量子電動力學系統已經研究了多種能夠產生微波光子糾纏的非線性效應(如動態卡西米爾效應、克爾效應等), 并通過實驗進行了驗證.

在量子理論中, 對電磁場進行量子化會發現真空零點能的存在. 而在非靜態真空腔中, 一個腔壁的快速運動可以使量子真空漲落(vacuum fluctuation)轉變成真實的光子, 這一現象被稱為動態卡西米爾效應. 動態卡西米爾效應本質上是一種通過外界擾動(例如介電常數、電導率等邊界材料的特性隨時間變化)改變量子場的模式結構, 進而從量子真空漲落中產生光子對的量子放大過程.2011年瑞典查爾姆斯工業大學Wilson等[47]在《Nature》上發表了關于測量動態卡西米爾效應的實驗, 他們利用基于可變邊界條件的微結構共面波導的超導電路實現了動態卡西米爾效應. 實驗中通過調諧超導量子干涉儀的磁通實現了對邊界條件的快速調制, 結果顯示測得了真空釋放的微波頻段的光子對, 并通過二階相干函數證明了雙光子的時空強相干特性[48,49], 如圖6所示. 在這一過程中,實光子對的能量來自于磁通對邊界條件的驅動(頻率為Ω), 而且微波光子對的頻率()之和等于邊界條件變化的頻率Ω, 即.

圖6 Wilson小組實驗裝置及超導量子干涉儀電子掃描照片[48]Fig. 6. The scanning?electron micrograph of the experiment?al device and SQUID of Wilson group[48].

基于卡西米爾效應產生微波糾纏光子對只是超導電路量子電動力學方法產生微波糾纏光子的一種. 目前, 以超導約瑟夫森結為核心的超導電路量子電動力學系統已經成為產生非經典微波的重要平臺, 即約瑟夫森–光子裝置. 多個團隊都對其產生微波糾纏光子進行了理論和實驗研究[50?54].在這種實驗系統里, 量子比特與兩個或多個微波傳輸線諧振腔耦合. 約瑟夫森結在兩個或多個耦合諧振腔(諧振于相同或不同的頻率)里分別產生微波光子, 其等效電路如圖7所示[51].

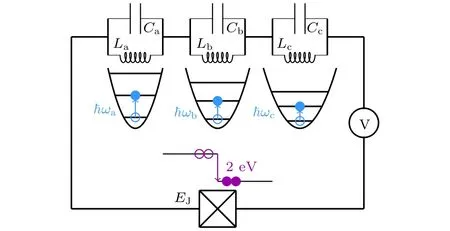
圖7 約瑟夫森–光子裝置等效電路原理圖[51]Fig. 7. Sketch of an equivalent circuit principle of Joseph?son?photonics device.

3.2.3 腔–光 (電)–力學系統

在腔–光(電)–力學系統中, 光或電與機械諧振子相互作用的非線性導致了很多非經典效應的產生, 使得這一體系成為重要的量子系統. 而電–光–力學系統由包含了機械振子的光腔和微波腔共同組成, 是腔–光–力學系統與腔–電–力學系統的集合[56]. 在該系統中, 機械振子既與光場耦合, 也與微波場耦合, 其結構如圖8所示. 目前未見到利用該類系統產生微波光子離散變量糾纏的方案. 而文獻[57–60]的研究表明, 將機械振子作為光頻光子與微波光子的量子接口, 可以利用電–光–力學平臺產生光場與微波場的糾纏.

利用藍、紅失諧激光分別驅動微波場和光場,此時的哈密頓量為

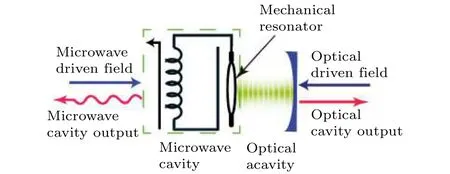
圖8 電–光–力學系統典型結構Fig. 8. The typical structure of electro?opto?mechanical sys?tem.

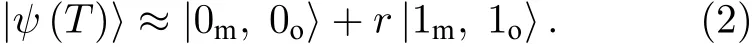
可判斷體系能夠產生微波場和光場的光子數糾纏, 且在某一時刻若檢測到光場為一個光子, 則微波場此時一定處于單光子態.

Barzanjeh等[61,62]提出一種基于電–光–力學系統的微波量子照射雷達. 該量子雷達系統利用機械振子將微波腔與光腔耦合, 產生微波光子與光波光子的糾纏, 并將微波作為雷達信號照射目標, 光波信號作為休閑信號保留在本地, 然后對微波的回波變換成光波再與光波休閑信號進行符合測量, 如圖9所示.

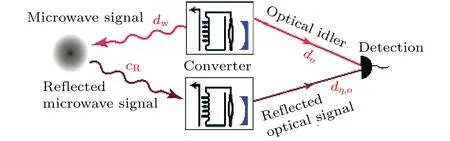
圖9 微波量子照射雷達示意圖[61]Fig. 9. Schematic of microwave quantum illumination.

3.3 壓縮態及糾纏態微波場的制備

按照量子噪聲特性可將連續變量量子微波場分為熱態微波場、相干態微波場、壓縮態微波場以及糾纏態微波場. 熱態和相干態微波場的產生相對容易, 本文不再展開論述, 主要分析壓縮態以及糾纏態微波場的產生原理與相關實驗進展. 壓縮態微波場可分為正交壓縮、振幅壓縮(光子數壓縮)和強度差壓縮微波場. 本文重點關注正交壓縮微波場的制備原理和實驗進展. 正交壓縮微波場是將微波場某個正交分量的量子噪聲壓縮到經典散粒噪聲極限以下的一種非經典微波場. 而壓縮態微波場通過分束器與真空態或熱態耦合, 可以產生連續變量糾纏微波場. 連續變量糾纏微波場的糾纏特性體現為子系統正交分量之間的非定域量子關聯[63]. 由于電磁場正交分量的糾纏與其耦合模的正交分量壓縮相互聯系, 故這種類型的糾纏又被稱為壓縮糾纏.

正交壓縮光場具有突破量子噪聲極限的特點,被廣泛應用于精密光學測量[64]和微弱引力波信號探測[65]等領域. 制備正交壓縮態光場的方法途徑很多, 目前已報道的不下數十種, 但按照產生原理基本可以分為參量過程、克爾效應和四波混頻等非線性效應過程. 參量過程可以認為是二階非線性效應的結果, 二階非線性效應可以用于實現三波混頻. 主要過程是將泵浦和信號輸入至非線性器件, 產生差頻信號即休閑信號, 結果使得,信號都得到放大, 如果則得到簡并參量放大和單模壓縮信號; 如果, 則得到非簡并參量放大, 但不會對任何一個模式產生壓縮效應, 而是使雙模之間產生關聯特性, 得到雙模壓縮態. 三階或更高階非線性可以產生克爾效應, 實現光子之間的相互作用. 四波混頻, 即一對泵浦光子產生信號光與休閑光的過程：, 就是三階非線性效應的結果. 壓縮微波場的制備完全可參照壓縮光場的制備原理和方法, 前提條件是能夠制備實現以上非線性效應的材料、器件或電路.

3.3.1 腔量子電動力學系統

腔量子電動力學系統利用原子(原子系綜、單原子或離子)和腔耦合(如囚禁在腔中二能級或多能級原子與腔模的相互作用)來制備壓縮態和糾纏態光場, 是產生非經典光場的重要途徑. 目前已有多種不同結構制備壓縮/糾纏光場的腔量子電動力學系統被提出并得到實驗驗證.

而在微波頻段, Pielawa等[66]提出了一種利用量子庫(quantum reservoir)(用于囚禁離子)產生雙模壓縮糾纏態的方案, 如圖10所示. 該方案中原子束起到原子庫的作用. 利用原子束泵浦諧振腔, 且無需控制原子到達順序, 但每次在諧振腔里只能有一個原子. 通過激光場和微波場的聯合作用控制入射原子束處于里德堡態和的相干疊加態(能級差對應于偶極躍遷), 原子束與高品質因數值微波諧振腔強耦合, 微波場飽和原子的偶極矩躍遷, 使微波腔諧振于兩個非簡并模式()上, 并逐漸演變并穩定于雙模壓縮態. 當原子從強驅動場吸收兩個光子, 則會在兩個場模邊頻上同時輻射兩個強相干光子, 即四波混頻的非線性過程, 這本質上對應于一個雙光子過程. 兩個場模諧振于原子偶極躍遷頻率的兩個拉比邊帶(Rabi sideband). 穩態時, 兩個場模處于EPR(Einstein?Podolsky?Rosen)糾纏態, 且糾纏度可由驅動光場強及頻率控制.

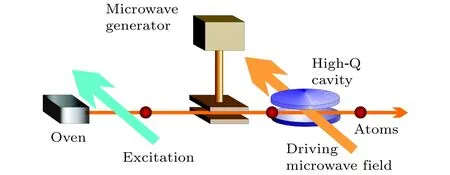
圖10 利用量子庫產生雙模壓縮態方案[66]Fig. 10. Scheme of generating two?mode squeezed state us?ing quantum reservoir.

理論研究表明, 超冷原子與超導傳輸線腔之間的磁耦合強度可以達到強耦合區, 利用超冷原子與超導傳輸線腔的強耦合, 李蓬勃和李福利[67,68]提出了一種制備傳輸線腔場雙模壓縮態的新方法, 并證明了在特定條件下超冷原子自旋波與腔場耦合體系可以看作參數可控的三個耦合量子諧振子體系. 在該方案中, 包含原子數為N的87Rb超冷原子系綜囚禁于超導傳輸線諧振腔表面, 如圖11所示. 通過對體系演化的相干控制, 在特定時刻超冷原子自旋波和腔場自由度分離, 而且此時腔場處于雙模壓縮態. 這一方案的優勢在于可以通過調諧外部經典場的強度和失諧量方便地對壓縮度進行調整, 并且具有較長的相干時間. 實際上該方案并不是一個典型的腔量子電動力學系統, 這里的諧振系統是超導傳輸線, 因此該方案是原子系綜與超導電路量子電動力學系統的結合, 但結構及工作原理與腔量子電動力學系統更加相似.

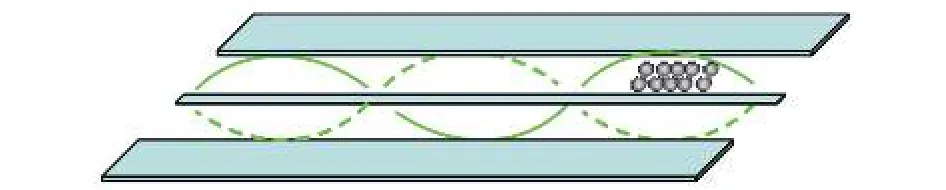
圖11 基于超冷原子與超導傳輸線腔耦合產生雙模壓縮態方案[67]Fig. 11. Scheme of generating two?mode squeezed state based on the coupling of ultracold atoms and superconduct?ing transmission line resonator.

3.3.2 超導電路量子電動力學系統

以約瑟夫森結為核心器件的超導電路是超導電路量子電動力學系統的主要研究對象. 其優越的超導特性實現了超低的能量耗散, 其諧振電路具有較高的品質因數. 更重要的一點是, 可等效為電感的超導約瑟夫森結在電路中表現出極強的非線性特征. 因此可以在宏觀尺度上實現這樣一種量子比特或人工原子. 而由于其比普通原子要大得多, 所以人工原子具有超大偶極矩(電或磁), 也因此在耦合電路的幫助下人工原子可以實現與電磁場較強的非線性相互作用. 而由于單微波光子能量低, 實現單微波光子的探測與應用較為困難, 目前基于正交位相、正交振幅等信息的連續變量量子微波場的研究較多, 在壓縮態微波場、連續變量糾纏微波場的生成與探測等方面取得了較大進展.

以超導約瑟夫森結為基礎構建的約瑟夫森參量放大器(Josephson parametric amplifier, JPA)是制備壓縮態微波場實驗中應用較多的器件. 約瑟夫森參量放大器是包含超導共面波導諧振器和超導量子干涉儀(superconducting quantum interfer?ence device, SQUID)的電路, 如圖12(a)所示. 它既可以實現微波信號的參量放大[69], 又能夠產生非經典的微波態[70], 還可以單點讀取超導磁通量子位[53]. 作為一種相敏放大器(phase sensitive amplifier), 它可以壓縮微波場的一個正交分量(具體是正交振幅分量還是正交位相分量取決于泵浦場信號與輸入信號的相位關系)的起伏, 而放大另一個正交分量上的起伏, 實現正交壓縮微波場. 而在這一過程中, 伴隨著泵浦光子分裂成信號光子和休閑光子的雙光子過程. Menzel等[71]利用該放大器首先實現了單模微波壓縮場, 然后與真空態在微波混合環分束器中混合, 實現了空間分離的頻率簡并連續變量微波糾纏. 這里的超導180°混合環(hybrid ring, HR)分束器工作原理類似于光學分束器[72], 它將真空態與約瑟夫森參量放大器產生的壓縮態混合, 分束的兩路信號表現出糾纏特性,如圖12(b)所示.

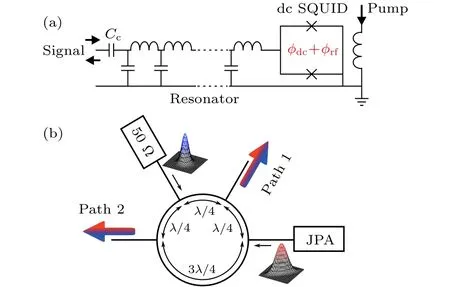
圖12 (a) 約瑟夫森參量放大器[71]; (b) 180°混合環微波分束器[72]Fig. 12. (a) Josephson parametric amplifier; (b) 180° hy?brid ring microwave beam splitter.

Eichler等[73]利用類似的約瑟夫森參量放大器產生壓縮態微波場, 明顯不同的地方在于, 該約瑟夫森參量放大器應用了三個超導量子干涉儀陣列作為非線性器件, 另外該參量放大器工作于非簡并模式, 實現四波混頻的作用, 即兩個泵浦光子生成一個信號光子和一個休閑光子, 產生雙模壓縮微波場. 空間上耦合在一起的雙模壓縮微波場經過高電子遷移率場效晶體管(high electron mobility transistor, HEMT)放大器放大后分成兩路, 各與一個本地振蕩信號進行差拍檢測, 獲取雙路信號共四個正交分量的全部信息, 進而驗證了其雙模壓縮特性, 如圖13所示.

Ku等[74]將壓縮場與真空場輸入微波分束器,在輸出端進行正交相關檢測, 驗證了兩個輸出模之間的糾纏特性, 如圖14所示.

約瑟夫森環形調制器(Josephson ring modu?lator, JRM)是另一種可以作為頻率轉換器或者相位保持參量放大器應用的非線性電路. 它包含四個約瑟夫森結, 為典型的惠斯頓電橋結構, 完全對稱,且具有無損耗、無噪聲以及強非線性特性. 其應用非常廣泛, 如固態量子位的讀取、頻率變換以及糾纏微波光子對的產生等[75,76]. Roch等[77]在約瑟夫森環形調制器的基礎上, 增加了四個交叉相連的線性電感, 設計了寬調諧的三波混頻設備. Flurin等[78]通過在這種電路上外加傳輸線和電容組成的諧振回路, 產生了空間分離的一對不同頻率的雙模壓縮微波場, 即連續變量微波糾纏信號, 這種設備稱之為約瑟夫森混頻器(Josephson mixer, JM), 如圖15所示.

圖13 四波混頻產生壓縮微波場[73]Fig. 13. Schematic of generating squeezed microwave field using four?wave mixing.

圖14 壓縮場與真空場耦合產生糾纏微波場[74]Fig. 14. Schematic of generating entangled microwave field using the squeezed field and vacuum field.

以上用于產生壓縮態或糾纏態微波場的超導電路量子電動力學系統, 具體電路結構可能有所差異, 但基本工作原理都是基于超導電路量子電動力學系統的核心器件–約瑟夫森結的非線性電感以及由此產生的其他非線性效應, 如二階非線性效應、克爾效應等, 而參量過程可以認為是二階非線性效應的結果, 四波混頻是三階非線性效應的結果.

3.3.3 腔–光 (電)–力學系統

圖15 約瑟夫森混頻器產生雙模壓縮微波場[78]Fig. 15. Schematic of generating two?mode squeezed mi?crowave field using Josephson mixer.

腔–光(電)–力學系統是近年來產生壓縮態、糾纏態微波場的重要研究平臺[79,80]. Caspar等[81]搭建了類似約瑟夫森參量放大器結構的腔–電–力學參量放大裝置, 產生了噪聲起伏比真空噪聲低8 dB的壓縮態微波場. 該裝置包含一個超導微波諧振腔(諧振頻率6.9148 GHz, 線寬為6.44 MHz),與一個直徑的振動薄膜耦合(振動頻率=10.319 MHz, 線寬為107 Hz), 諧振腔由包含兩個頻率()的電壓信號驅動,表示相對共振頻點的失諧. 兩個系統通過微波輻射壓耦合, 在過耦合狀態, 機械振子不會吸收任何能量而將微波場完全反射, 如圖16所示. 該實驗系統可以看作約瑟夫森參量放大器產生單模壓縮態微波場的實驗方案在腔–電–力學系統中的對應.

Li等[82]利用腔–電–力學平臺制備了雙模壓縮糾纏態微波場, 其結構是利用納米結構機械振子將兩個超導共面波導諧振腔耦合, 如圖17所示. 該結構與超導電路量子電動力學系統中的約瑟夫森–光子裝置非常相似, 只是中間的非線性耦合器件由人工原子變成了機械振子. 機械振子的機械移動改變了電路電容, 使兩個諧振腔與機械振子產生了參量耦合效應, 結果使得兩個諧振腔之間產生了相互作用. 可以通過調整該實驗裝置電容上的驅動電壓來改變諧振腔與機械振子的機電耦合強度, 進而調整產生的雙模壓縮糾纏態的糾纏度. 其中驅動電壓,,分別為兩個微波諧振腔和機械振子的諧振頻率.

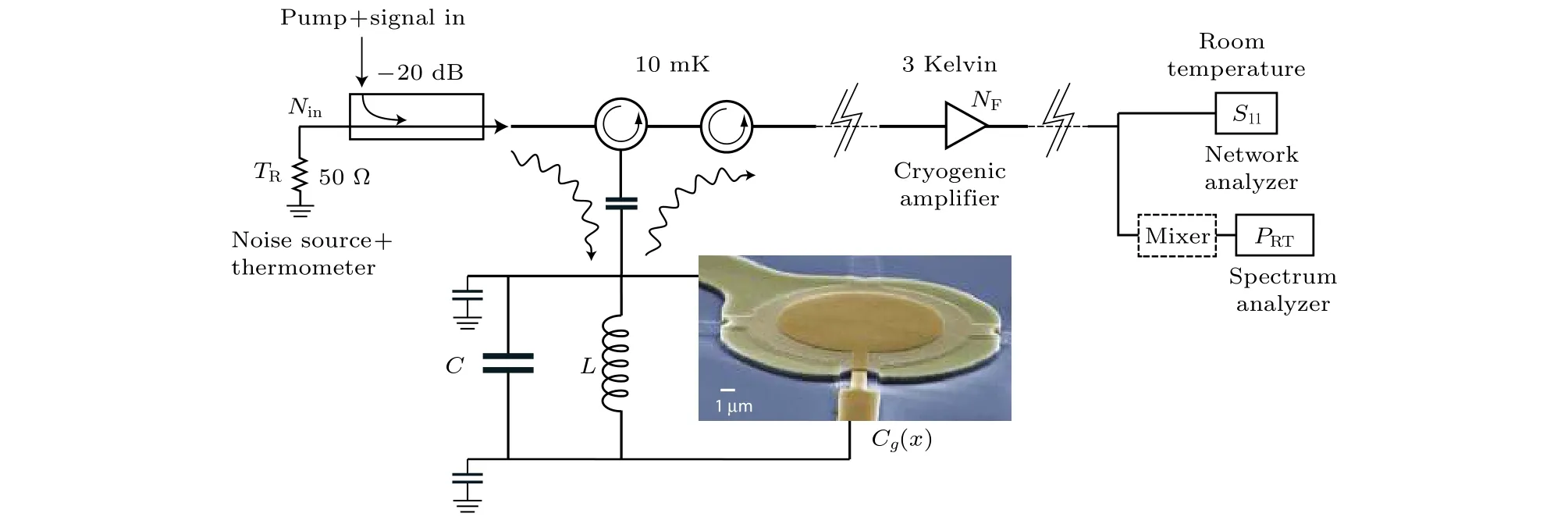
圖16 基于腔–電–力學系統的微波參量放大裝置[81]Fig. 16. The microwave parametric amplifier device based on cavity electromechanics system.

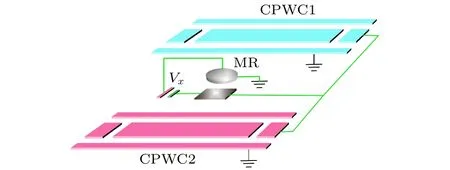
圖17 基于腔–電–力學系統的雙模壓縮微波場產生裝置[82]Fig. 17. Device of generating two?mode squeezed mi?crowave field based on cavity electromechanics system.

Sete和Eleuch[83]利用超導電路量子電動力學與腔–電–力學的聯合系統研究了微波壓縮場的產生以及微波場與機械振子的糾纏, 系統結構如圖18所示. 超導量子比特與傳輸線諧振腔TLR1以及微機械振子耦合, 機械振子再與另一個傳輸線諧振腔TLR2耦合. 在強耗散極限下, 超導量子比特與TLR1以及微機械振子的耦合會使傳輸線諧振腔與機械振子產生非線性耦合作用, 此外TLR2也會與機械振子產生非線性作用. 實驗表明, 即使存在熱噪聲, 兩種非線性作用的聯合效應也能夠實現微波場的強壓縮, 且壓縮度可通過調整泵浦微波場的功率來控制.

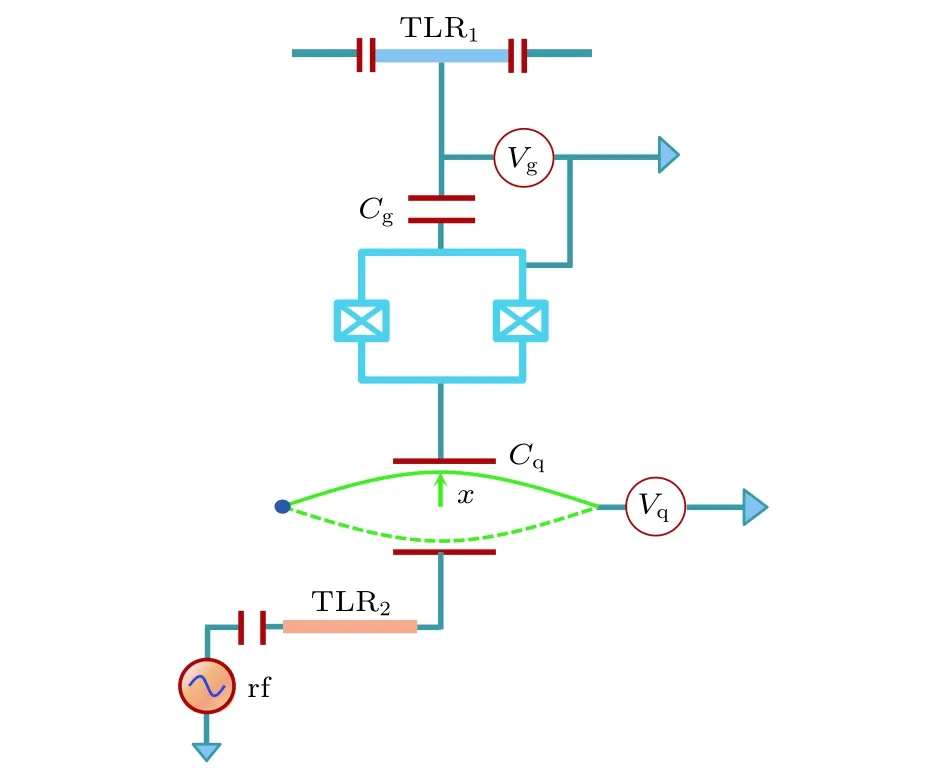
圖18 超導電路量子電動力學與腔–電–力學的聯合系統制備壓縮微波場[83]Fig. 18. The jointed system of circuit quantum electro?dynamics and cavity electromechanics system that generat?ing squeezed microwave field.

此外, 集合了腔–光–力學系統與腔–電–力學系統的電–光–力學系統也可以制備非經典微波場. 在電–光–力學系統中, 機械振子既與光場耦合, 也與微波場耦合. 若使微波場和光場都受紅失諧激光驅動, 此時微波場和光場與機械振子均形成線性混合的相互作用, 使得二者均與機械振子形成量子態的交換, 因而機械振子可以成為光場與微波場的量子接口, 實現二者量子態的轉移或者傳遞[84,85]. 因此,利用電–光–力學系統, 選擇紅失諧激光驅動微波腔和光腔, 在光腔中輸入壓縮態光場, 利用微波場和光場之間的量子態轉換, 在體系耗散系數很小時,微波腔中可制備出髙保真度的壓縮態微波場, 即利用量子態的轉移實現微波非經典態. Palomaki[86],Tian[60]以及Wang和Clerk[87]分別研究了在高斯態、貓態、單模壓縮態和光子數態下, 不同熱環境從光場到微波場間量子態的轉移保真度及其演化.

利用機械振子作為光場與微波場的量子接口,Abdi等[88]設計了直接產生連續變量糾纏微波場的電–光–力學方案, 如圖19所示.

圖19 連續變量糾纏微波場的電–光–力學產生方案[88]Fig. 19. Scheme of electro?opto?mechanical system to gener?ate continuous variable entangled microwave field.

該方案包含兩個相隔一定距離的電–光–力學系統Alice和Bob. 同樣在每一個電–光–力學系統中利用藍、紅失諧激光分別驅動微波場和光場, 實現微波場和光場的糾纏. 相比微波場, 光場受退相干影響較小. Alice和Bob將光學模送至二者中間的Charlie, 對兩個光學模進行貝爾態測量, 通過連續變量糾纏交換使空間相隔一定距離的兩個微波場糾纏起來.

4 量子微波場在微波量子導航中的問題探討

量子微波場的生成為微波頻段量子信息處理、量子密集編碼, 特別是微波量子通信、微波量子雷達以及量子超精密測量等基于空間傳輸的量子信息技術提供了可資利用的重要信號源. 而且由于微波場相對于光頻信號具有更強的云霧穿透能力, 抗大氣衰減能力強, 因此其在空間中的遠距離傳播能力更有利于量子微波信號大尺度動態空間環境中的量子信息傳輸應用, 甚至會對傳統的通信、導航、雷達等領域產生顛覆性影響. 作者與研究團隊近年來持續跟蹤量子微波場的研究進展, 并在連續變量糾纏微波信號在無線電導航中的應用問題做了一些研究工作[89?91]. 利用量子糾纏微波信號實現在粒子性層面運用電磁場的無線電導航, 依靠糾纏粒子強關聯、隱形傳態等特性, 建立起新型無線電導航系統體制, 能夠大幅提升無線電導航參數量測精度、弱信號檢測能力、保密抗干擾等性能水平,占據信息化戰爭條件下獲取安全可靠導航信息的優勢地位. 然而, 從實驗室制備產生量子糾纏微波信號到實現在具體系統中的現實應用, 還有一系列理論和工程技術問題亟待解決.

4.1 量子糾纏微波信號生成能力問題

目前, 已有研究團隊成功制備了連續變量量子糾纏微波信號, 特別是Menzel團隊利用約瑟夫森參量放大器以及Flurin團隊利用約瑟夫森混頻器產生了空間分離的糾纏微波信號, 為利用其糾纏特性奠定了技術基礎. 然而, 目前糾纏微波信號的生成能力是有限的, 實驗中制備的信號功率水平較低. 將糾纏微波信號應用于實際的無線電導航系統, 首先要解決的問題就是這種基于約瑟夫森結的量子糾纏微波信號生成能力的問題, 即如何提高所產生的壓縮態、糾纏態微波場的輻射源功率、壓縮度、糾纏度等性能指標, 以及降低對實驗環境、實驗條件要求的問題.

4.2 量子糾纏微波信號傳輸信道退相干問題

量子糾纏微波導航信號的無線傳播環境是一個量子系統與自由空間環境相互作用的開放系統.糾纏信號在信道傳輸過程中, 因量子系統與周圍環境的相互作用將環境的各種參數引入而使問題變得過于復雜, 自由空間傳輸衰減、湍流和非線性效應會引起糾纏度的下降, 導致應用系統的工作基礎–糾纏微波相干性能的破壞. 總的來說, 糾纏微波信號在自由空間的傳播問題主要有三個方面：一是能量損耗問題; 二是與大氣中物質作用引起的退相干問題; 三是空間形狀散射導致的能量擴散和部分檢測問題. 目前, 糾纏微波信號的傳播與量測都是在波導及微帶傳輸線中進行的, 基本不存在這些問題. 但若向空間輻射糾纏微波信號, 上述問題不可避免.

4.3 量子糾纏微波信號接收檢測問題

量子糾纏微波信號經過自由空間傳輸的衰減,到達接收方天線時能量已經非常弱, 甚至遠低于電路噪聲. 因此, 需要在接收端解決信噪比的提高(如采用壓縮真空注入及相敏放大等量子增強技術)以及糾纏微波信號的最優量子接收和檢測問題. 此外, 如何有效利用量子糾纏微波信號的非經典特性, 在現有零拍檢測及雙路徑接收檢測方法的基礎上, 探尋最適宜的接收檢測方法, 將其非定域關聯特性與無線電導航技術有效結合, 也是下一步工作中需要解決的重點問題.

5 小結與展望

盡管微波頻段量子信息技術的研究和應用要比光學頻段發展緩慢, 但由于微波受大氣環境影響較小, 云霧穿透能力和遠距離傳播能力較強, 量子微波場的生成為微波頻段量子信息處理、量子密集編碼, 特別是微波量子通信、微波量子雷達以及量子超精密測量等基于空間傳輸的量子信息技術提供了可資利用的重要信號源. 對于未來量子微波的研究方向與發展路線, 我們主要有以下三個方面的設想： 一是在內部冷凍機中進行實驗, 完成連續變量量子微波隱形傳態、微波量子照明等實驗的原理性論證, 伴隨著需要開發和制造足夠高效率的微波光電探測器. 二是在內部冷凍機之間進行實驗, 將一束微波留在冷凍機中, 而另一束通過高噪聲的波導或微帶傳輸線傳輸, 在與低反射率的目標對象相互作用后, 通過探測反射信號來確定目標對象存在與否. 這一實驗和技術的進步需要得益于設計熱光子濾波器以及基于約瑟夫森材料的小型延遲線. 三是利用天線輻射和接收量子微波信號, 在開放空間中進行上述實驗的驗證. 適用天線理論模型的發展和材料的選擇、形狀的設計等都將是其中最關鍵的工作.

本文主要綜述了近年來對量子微波場制備與探測理論技術與相關的實驗研究進展, 具體以量子糾纏微波導航為例指出了量子微波信號在自由空間量子信息傳輸系統應用中的若干需要關注的問題, 并簡要展望了未來量子微波技術的發展方向.希望為正在從事或有興趣從事量子微波技術相關研究的學者提供有益的參考.