基于彈載捷聯慣性導航系統精確導航的雙歐拉全姿態方法

呂維維，程向紅，邱 偉

(1. 東南大學 微慣性儀表與先進導航技術教育部重點實驗室，江蘇 南京 210096； 2. 東南大學 儀器科學與工程學院， 江蘇 南京 210096； 3. 上海宇航系統工程研究所，上海 201109)

0 引言

捷聯慣性導航系統(SINS)是一種不依賴于任何外部信息，也不向外部輻射能量的自主導航系統。該系統具有隱蔽性好、導航精確的優點，在戰術導彈、運載火箭、宇宙飛船、飛機、艦船上有著廣泛應用[1-2]。作為SINS的核心，姿態更新算法在SINS精確導航中發揮著重要作用，這些算法主要有方向余弦法、四元數法、歐拉角法[3-5]等。其中：方向余弦法更新姿態矩陣需求解9個微分方程，求解的姿態矩陣可全姿態工作，但計算量較大[3]；四元數法計算量小、計算精度高，但每次求解到的姿態矩陣必須經過正交化的誤差修正處理，在飛行過程中會出現有界參數誤差出界的情況[6-8]；歐拉角法求解歐拉角只需求解3個微分方程，與其他算法相比，需要求解的方程個數最少，且求解到的姿態矩陣永遠是正交陣，無需正交化處理，但歐拉角系統有1對奇異點，在奇異點附近會產生解算誤差，使輸出姿態角發生突變，無法準確定值[2, 9-10]。

為解決歐拉角奇異性的問題，黃雪樵[6]最早對雙歐法進行了理論論證，認為雙歐法能有效消除單歐法奇異點。SINGLA等[11]對序貫旋轉法(MSR)進行了詳細研究，并指出采取不同歐拉角組合、相互切換的方法比MSR方法更簡潔。陳廷楠等[12]將雙歐法與四元數法進行了理論對比，證明四元數法存在較大的累計計算誤差，雙歐法在克服歐拉角奇異性的問題上優于四元數法。以上學者主要進行理論研究，對雙歐法的應用研究較少，對四元數法與雙歐拉法解算精度的對比研究也較少。為適應現代戰爭的需要，目前戰術導彈已逐漸采用大攻角控制方式，實現大機動飛行。對于垂直發射的地空導彈，為使導引頭能成功捕獲目標，要求對導彈姿態進行精確控制。傳統方法使用四元數表示彈體姿態，并對姿態控制進行系統設計，然而四元數法在彈體俯仰角90°時只能進行姿態矩陣更新，無法正常輸出姿態角，這給大機動地空導彈的姿態控制帶來了困難。

本文針對垂直發射的地空導彈在大機動飛行時姿態解算容易出現奇異值的問題，將正、反歐拉角切換的雙歐拉全姿態算法應用到姿態解算過程中，通過半物理試驗驗證了該方法的有效性。

1 正、反歐拉角方程

1.1 歐拉角法

動坐標系相對參考坐標系方位，由動坐標系依次繞3個不同軸轉動的3個轉角來確定[6]，如圖1所示。令O-XbYbZb為動坐標系，O-ENU為參考坐標系，則航向角H、縱搖角P、橫滾角R為1組歐拉角。

圖1 彈體空間角位置的確定Fig.1 Determination of missile’s space position

兩坐標系間的變換矩陣等于基本旋轉確定變化矩陣的連乘，順序根據基本旋轉先后次序從右向左排列。圖中，彈體空間角位置確定依據為

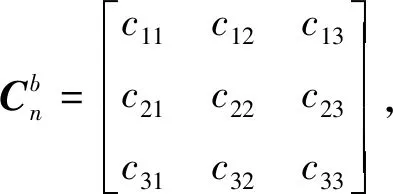
令導航坐標系為n，彈體坐標系為b，則姿態矩陣可表示為

(1)

(2)

1.2 正、反歐拉角微分方程

彈體的姿態變化可看作依次繞航向軸、俯仰軸、橫滾軸進行基本旋轉后的復合結果[1, 10]，即

(3)

(4)

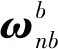
(5)

將式(5)轉換為歐拉角微分方程，具體表示為

(6)

(7)

由式(6)可知，歐拉角微分方程包含三角函數運算，給實時計算帶來困難，當俯仰角P=90°時，歐拉角微分方程出現奇異點，使計算溢出。

(8)

(9)

(10)

式(8)～(10)中：P=±90°為方程組奇異點，但當P=0或P≈±180°時，方程解的精度會提高，此求解范圍稱為正歐拉方程解的精華區。

(11)

將式(11)轉換為

(12)

(13)

(14)

(15)

從反歐拉方程來看，奇異性問題同樣存在，即Rr=±90°是方程組的奇異點；當Rr=0或Rr=±180°時，方程解的精度會提高，此求解范圍稱為反歐拉角微分方程解的精華區。

2 正、反歐拉角的轉換關系

任意2個坐標系之間的變換矩陣是唯一的，因此正、反歐拉角的變換矩陣對應項相等，分別表示為

(16)

L(Pr,Rr,Hr)=

(17)

由式(16)，(17)可得，cosRr=sinP/sinPr，將cosRr代入式(13)～(15)中，則反歐拉角微分方程可變換為

(18)

(19)

(20)

圖2 正、反歐拉角微分方程的精華區與奇異區Fig.2 Essence areas and singular areas of positive and reverse Euler angle differential equations

由式(18)～(20)可見，反歐拉角微分方程與正歐拉角微分方程相反，其精華區在P=±90°附近，奇異區在P=0或P=±180°附近。若以±45°和±135°為界進行劃分，則正、反歐拉角微分方程的精華區與奇異區如圖2所示。由圖可知：正、反歐拉角微分方程的精華區與奇異區正好呈倒置關系。充分利用該關系實現兩者的無縫切換：當|P|≤45°或|P|>135°時，求解正歐拉角微分方程，發揮正歐拉角精華區解算精確的優點；當|P|>45°且|P|≤135°時，求解反歐拉角微分方程，利用反歐拉角精華區進行姿態解算，有效避免俯仰角在±90°附近姿態角突變的問題。

由于正、反歐拉角變換矩陣的一致性，因此正歐拉角變換矩陣與反歐拉角變換矩陣的對應項相等，其定義為

由式(16)～(17)得到正歐拉角到反歐拉角的變換關系式，即

(21)

式中：Rr≠±π/2。反之，反歐拉角到正歐拉角的變換關系式為

(22)

式中：P≠±π/2。針對地空導彈的大機動運動，利用雙歐拉全姿態算法，交替采用正、反歐拉角來描述姿態。地空導彈正、反歐拉角微分方程的全姿態解算流程如圖3所示。由圖可知，其解算步驟為：1)初始化系統，輸入慣性測量單元(IMU)信息。2)對正歐拉角俯仰角P的絕對值進行判斷，當|P|≤45°或|P|>135°時，符號標志位Flag=1，此時求解正歐拉角微分方程；當|P|>45°且|P|≤135°時，Flag=-1，此時求解反歐拉角微分方程。整個姿態解算的持續時間設為T，當導航時間達到T時解算結束。

圖3 地空導彈正、反歐拉角微分方程全姿態解算流程Fig.3 Flow chart of positive and reverse Euler angle differential equations’ whole attitude solution

3 試驗驗證

3.1 仿真驗證

為驗證地空導彈雙歐拉全姿態算法的非奇異性，進行了仿真驗證。仿真參數設置情況見表1。姿態解算周期為0.01 s，仿真經度為118.8° E，緯度為32.06° N。在仿真過程中，IMU航向角H=0°，橫滾角R=0°，俯仰角周期性搖擺，正弦函數為A·sin(2πf·t+φ0)+ψ0。其中：A為IMU的搖擺幅值，A=90°；f為搖擺頻率，f=(1/256)Hz；φ0為搖擺初始相位，φ0=0°；ψ0為搖擺中心，ψ0=0°。仿真時間為2 500 s。

表1 傳感器參數設置

整個仿真過程中，IMU俯仰角在±90°附近周期性搖擺，姿態解算采用四元數算法。經過2 500 s的仿真，IMU實際解算姿態角與理論姿態角的對比如圖4～6所示。

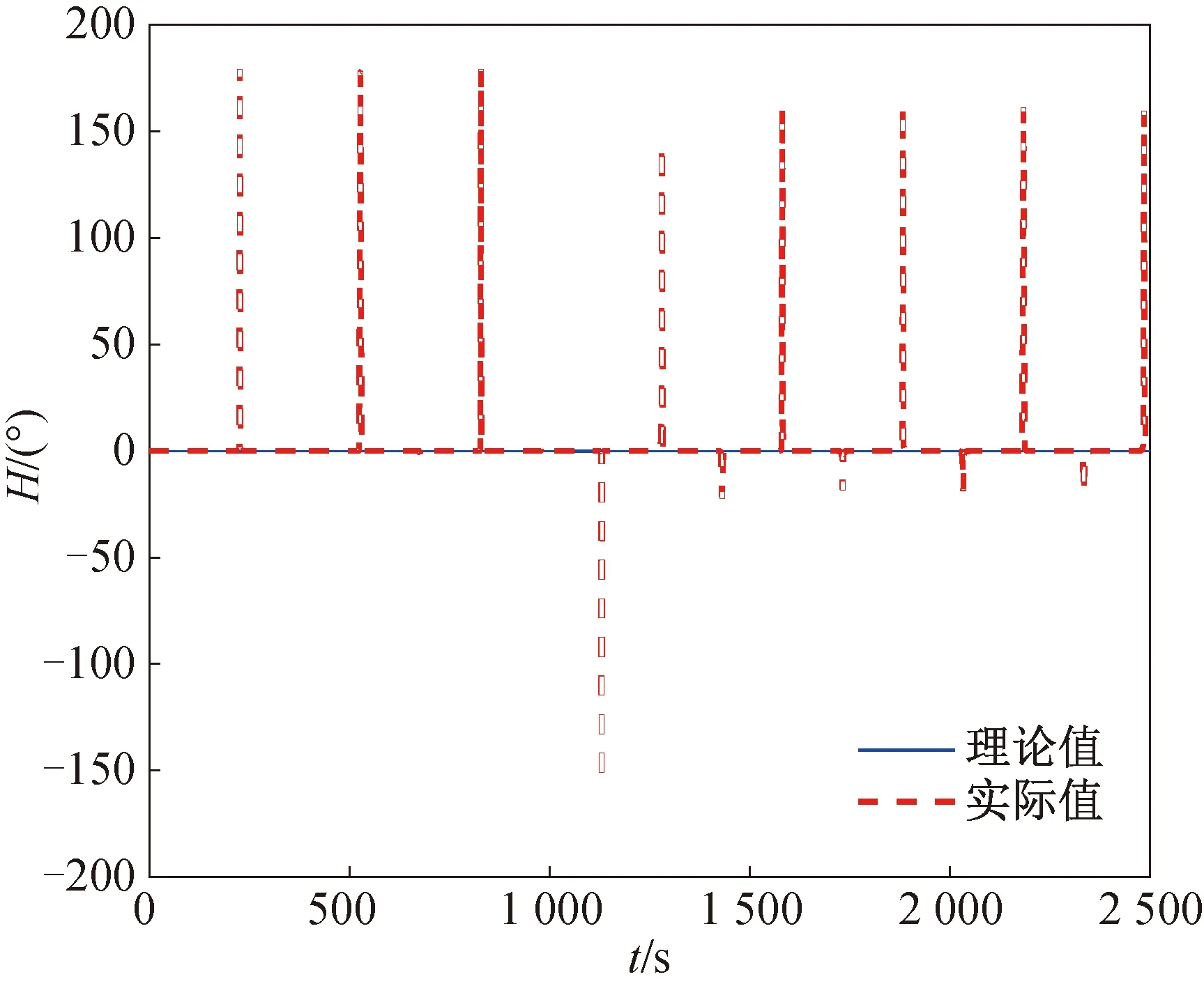
圖4 四元數法航向角的理論值與實際值比較Fig.4 Comparison of heading angle’s theoretical value and actual value by using quaternion method

圖5 四元數法俯仰角的理論值與實際值比較Fig.5 Comparison of pitching angle’s theoretical value and actual value by using quaternion method

圖6 四元數法橫滾角理論值與實際值比較Fig.6 Comparison of rolling angle’s theoretical value and actual value by using quaternion method

由圖4～6可知：當姿態解算采用四元數算法時，由于IMU俯仰角為±90°時只能進行姿態更新，無法正常輸出姿態角，因此IMU輸出的實際航向角和橫滾角均發生突變，姿態角出現奇異現象。

為進行對比，在同樣條件下采用雙歐拉全姿態算法進行姿態解算，IMU實際解算的姿態角與理論姿態角的對比情況如圖7～9所示。

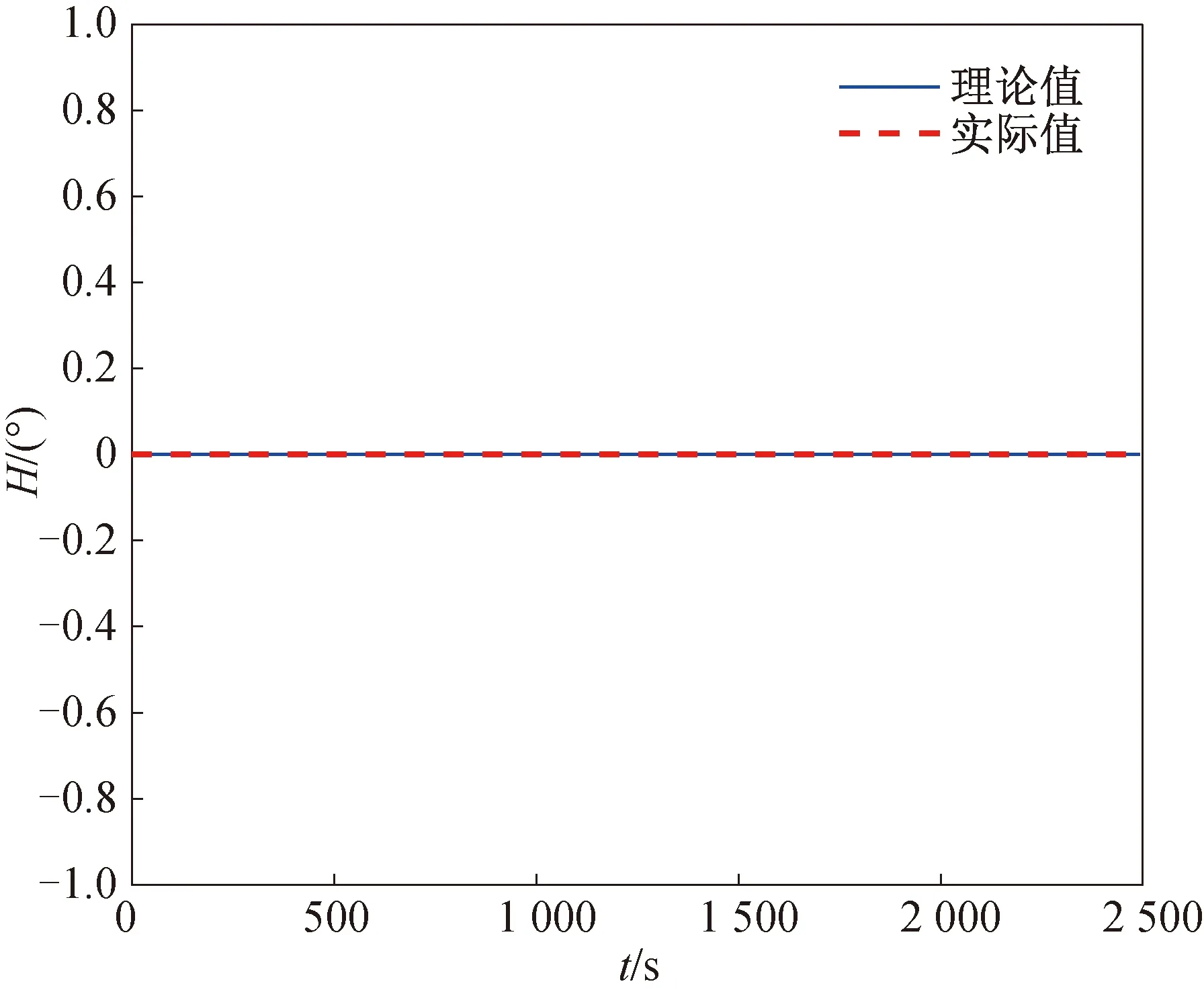
圖7 雙歐拉法航向角理論值與實際值比較Fig.7 Comparison of heading angle’s theoretical value and actual value by using dual-Euler method

圖8 雙歐拉法俯仰角理論值與實際值比較Fig.8 Comparison of pitching angle’s theoretical value and actual value by using dual-Euler method

圖9 雙歐拉法橫滾角理論值與實際值比較Fig.9 Comparison of rolling angle’s theoretical value and actual value by using dual-Euler method

由圖7～9可知：當采用雙歐拉全姿態算法后，IMU實際解算的航向角、橫滾角與理論值基本重合，未出現突變為-180°或180°的現象。理論俯仰角與實際俯仰角基本重合，在±90°附近能正常輸出姿態，未出現突變現象。雙歐拉全姿態解算的實際姿態、理論姿態的誤差曲線分別如圖10～12所示。

圖10 雙歐拉法航向角誤差Fig.10 Error curve of heading angle by using dual-Euler method

圖11 雙歐拉法俯仰角誤差Fig.11 Error curve of pitching angle by using dual-Euler method

圖12 雙歐拉法橫滾角誤差Fig.12 Error curve of rolling angle by using dual-Euler method

由圖10～12可知：在解算過程中，航向角誤差緩慢變大，但誤差絕對值在0.5′以內。俯仰角誤差因IMU周期性搖擺而上下波動，但誤差絕對值在1′以內。橫滾角誤差隨時間增長而緩慢變大，但誤差絕對值在0.6′以內。當運用正歐拉角更新時，Flag=1；當運用反歐拉角更新時，Flag=-1。俯仰角在±90°搖擺時Flag的變換情況如圖13所示。

圖13 雙歐拉法正、反歐拉角微分方程切換標志Fig.13 Switch flag of positive and reverse Euler angle differential equations by using dual-Euler method

3.2 半物理驗證

為進一步驗證地空導彈雙歐拉全姿態算法的有效性，在三軸轉臺上進行了半物理試驗。轉臺試驗實物如圖14所示，該轉臺的轉動速率精度為±0.000 5(°)/s，角度測量精度為±0.000 1°，可認為轉臺輸出是沒有誤差的理論姿態。在半物理試驗中，轉臺外框、中框、內框分別控制IMU的航向角、俯仰角、橫滾角轉動。試驗采用某型撓性慣組作為IMU，其中三軸陀螺儀的隨機常值漂移為0.025 (°)/h，隨機噪聲為0.01(°)/√h，三軸加速度計的隨機常值偏置為0.1 mg，隨機噪聲為0.05 mg/√Hz。IMU的姿態更新周期為0.01 s。試驗中，轉臺外框和內框始終保持靜止(H=0，R=0)，轉臺中框先靜止一段時間，然后以約0.015 (°)/s的固定轉動速率在±90°之間周期性轉動。

圖14 轉臺試驗實物Fig.14 Actual turntable test

試驗總共進行2 500 s，導航計算機實時記錄轉臺輸出姿態、IMU輸出角速度、加速度信息。導航計算機采用雙歐拉全姿態算法對陀螺儀和加速度計輸出進行捷聯解算。給出俯仰角姿態解算結果，解算得到的實際俯仰角與轉臺輸出理論俯仰角的比較如圖15所示。

圖15 雙歐拉法俯仰角理論值與實際值比較Fig.15 Comparison of pitching angle’s theoretical value and actual value by using dual-Euler method

圖16 雙歐拉法俯仰角誤差曲線Fig.16 Error curve of pitching angle by using dual-Euler method

由圖15可知：雙歐拉全姿態算法得到的IMU俯仰角曲線與轉臺輸出俯仰角曲線幾乎重合。即使轉臺輸出角速率因人為操作而出現小的波動，IMU解算的姿態角也能很好跟蹤。當俯仰角接近±90°時，導航計算機能正常輸出俯仰角，未出現突變為-180°或180°的現象。雙歐拉全姿態算法解算的俯仰角與理論俯仰角的誤差曲線如圖16所示，解算出的俯仰角與理論俯仰角的誤差大致在±2′之間波動，誤差值保持穩定。

半物理試驗正、反歐拉角微分方程切換時Flag的變化情況如圖17所示。由圖可見：Flag的變化與IMU俯仰角大小的變化保持一致。

圖17 雙歐拉法正、反歐拉角微分方程切換標志Fig.17 Switch flag of positive and reverse Euler angle differential equations by using dual-Euler method

3.3 雙歐拉全姿態方法與四元數法的精度比較

垂直發射的地空導彈為了使導引頭能夠成功捕獲目標，對導彈的姿態精度和導航精度提出了很高的要求。但目前，對雙歐拉方法進行理論研究的文獻很少有雙歐拉方法與四元數法導航精度比較的報道。為比較本文提出的地空導彈雙歐拉全姿態方法與傳統四元數方法的導航精度，進行了半物理純慣性導航試驗。試驗進行了2 500 s，分別記錄不同時刻采用雙歐拉法和四元數法所得的純慣性導航位置誤差，對比情況見表2～4。

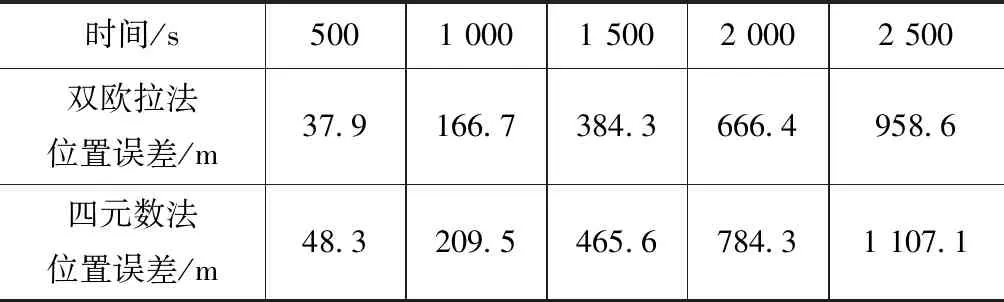
表2 純慣性導航東向位置誤差

表3 純慣性導航北向位置誤差

表4 純慣性導航位置誤差

由表2～4可知：在不同時刻采用雙歐法所得的純慣性導航東向位置誤差、北向位置誤差、位置誤差均小于采用四元數法所得的誤差。采用四元數法每次求解到的姿態矩陣必須經過正交化的誤差修正，不可避免存在近似誤差，且隨著計算時間的增加，誤差逐漸變大。由于雙歐拉法無需正交化處理，因此無近似誤差的累積。由表4可知：當時間為500 s時，雙歐拉法的位置誤差比四元數法的位置誤差減小了9.81%；當時間為2 500 s時，雙歐拉法的位置誤差比四元數法的位置誤差減小了13.14%。隨著時間的增加，雙歐拉法的導航精度比四元數法的導航精度更高。

4 結束語

地空導彈在大機動飛行時，其俯仰角在±90°附近會因奇異性而造成姿態角輸出突變。為解決該問題，本文提出了雙歐拉全姿態解算方法。通過推導正、反歐拉角微分方程，證明正、反歐拉角微分方程的精華區與奇異區呈倒置關系。根據俯仰角將正、反歐拉角微分方程進行切換，避免微分方程在奇異區內求解所產生的奇異性。詳細分析了正、反歐拉角的內在聯系，建立了兩者的轉換關系，實現兩者的無縫切換。為驗證地空導彈雙歐拉全姿態算法的有效性，進行了仿真試驗與半物理試驗,結果表明：由雙歐拉全姿態算法得到的彈體俯仰角，在±90°附近與理論俯仰角一致，未出現姿態突變現象。將雙歐拉全姿態解算方法與四元數法的導航精度進行試驗對比，結果表明：前者導航精度更高，未出現誤差累積現象。本文方法能保證地空導彈在大機動飛行時姿態角正常解算和輸出，對于彈載SINS在大機動飛行時的全姿態解算具有較高的工程應用價值。后續將對大機動飛行實際系統中的導彈進行進一步測試，以驗證該方法的穩定性和精確性。