一般性拱軸線偏差對拱橋內力和穩定性的影響
(重慶交通大學 重慶 400047)
拱作為一種以受壓為主的結構,最為理想的拱軸線是與拱上各種荷載的壓力線重合,在這種情況下,拱結構的各截面上只會存在軸向的壓力且分布均勻。然而,對于實際工程而言,拱軸線偏離合理狀態的情況幾乎不可避免。
一、拱軸線偏差對拱橋內力的影響
(一)水平推力
(1.1)
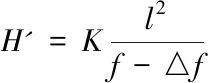
(1.2)
因為矢高變化量f△一般很小,則水平推力的變化率可簡化為:
(1.3)
又因為△f?f,由上式(1.4)可知,拱圈內的水平推力對矢高變化的響應不大。
(二)軸線偏差引起的彎矩
假定原設計拱軸線為y0,成橋時實際拱軸線為y,則實際拱軸線較設計拱軸線的偏差為δ=y-y0;假定成橋時實際恒載壓力線為y恒,則實際拱軸線較實際恒載壓力線的偏差為η=y-y恒。由系統余能公式可得:
(1.4)
M=Нη=Н(y-y恒)
(1.5)
由上述可知,主拱圈任意截面的彎矩M與其對應的實際拱軸線較實際恒載壓力線的偏差η有一定的函數關系。
二、拱軸線偏差對穩定性的影響
(一)面內軸線偏差
假設某一反對稱的軸線偏差為:δ=αsin(2πx/l0),則拱軸線的壓桿微分方程可以寫成:
(1.6)
設:k2=Na/EIZ,則
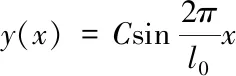
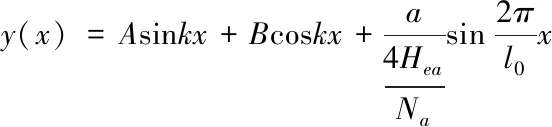
(1.7)
其中y(0)=y(l)=0,則式(1.9)改寫為:
(1.8)
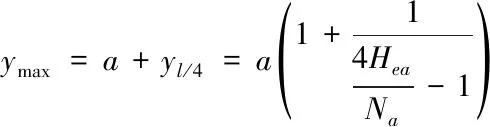
綜上所述可得:
1.式中4Hea/Na=λa是穩定安全度,對于理想桿的臨界平衡條件應為λa=1,當λa<1時,出現分支點失穩。由上式可知,當存在初始偏差a時,λa=1,則ymax→∞,表現為結構失穩。這說明拱結構失穩模態由第一類失穩(分支點失穩)變換為第二類失穩(極值點失穩)的根本原因是拱軸線平面內偏差的出現。
2.對于正對稱偏差δ=asin(πx/l0)和反對稱偏差δ=asin(2πx/l0)而言,若其偏差δ相同,則正對稱偏差的a小于δ,而反對稱偏差的a與δ相近,因此,正對稱偏差的總附加繞度ymax比反對稱偏差的要小,即穩定安全度更高,更不易失穩。
(二)面外軸線偏差
假設面外的拱軸線初始偏差:b(x)=b1sin(πxL0)
由此同理可建立平面外微分方程:
(1.9)
設:k2=Nb/EIy,則
上式一般解為:z(x)=Asinkx+Bcoskx,
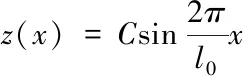
(1.10)
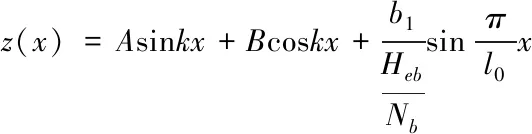
(1.11)
其中z(0)=z(l)=0,則式(1.14)改寫為:
(1.12)
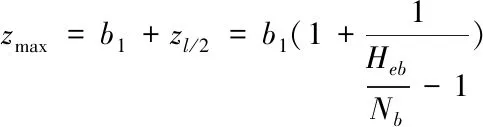
綜上所述可得:
面外和面內軸線偏差的情況類似,同樣會使得拱結構失穩模態由第一類失穩變換為第二類失穩,即失穩狀況提前出現。但是與面內軸線偏差不同的是臨界荷載取值不同,一般情況下比4Hea要大很多。
三、結論
1.拱橋施工中由于拱圈線形的變化,導致了恒載壓力線也作出了相應的變化。因此,若仍以原設計拱軸線作為基礎來控制拱圈軸線的偏差或對偏差進行評定,是不夠準確的。
2.對于水平推力而言,其對一般性的拱軸線偏差的響應不明顯,而彎矩對拱軸線偏差的響應情況就要看具體偏差的大小和類型了。正對稱的軸線偏差,其軸力N、彎矩M的響應都很小。反對稱的軸線偏差,由于反對稱的軸線偏差水平夾角φ大,則其軸力不可忽略,為N=Н/cosφ,且η近似的等于a,則由偏差引起的彎矩為M=Нa。
3.面內和面外兩種軸線偏差都會使得拱結構從第一類失穩轉換為第二類失穩,而拱軸線初始的偏差又使得拱結構的失穩狀態提前。對于一般性拱軸線偏差,即正對稱和反對稱偏差,當偏差相同時,正對稱偏差引起的遠小于,反對稱偏差引起的更接近,因此正對稱偏差比反對稱偏差穩定安全度更高,更不易失穩。

