徑向聲子晶體隔聲特性?

王興國 舒海生 張 靚 劉秀林 王鳳娟

(1齊齊哈爾大學機電工程學院 齊齊哈爾 161006)

(2哈爾濱工程大學機電工程學院 哈爾濱 150001)

(3黑龍江交通職業技術學院 齊齊哈爾 161002)

0 引言

聲子晶體作為一種人工周期結構功能材料，具有控制波傳播的特性，從而受到了學界的廣泛關注[1?5]。近年來，聲子晶體在帶隙理論和帶隙算法方面均取得重要進展。聲子晶體模型是借鑒和模仿自然晶格結構形式，即在直角坐標系中構造聲子晶體模型，這種周期性結構在一定程度上已經制約了該領域的進一步發展。在聲子晶體帶隙的產生本質上應根源于其內在的平移周期性，然而我們認為能夠激發帶隙的并不僅限于這種周期特性。目前，我們已經做了一些廣義聲子晶體方面的研究[6?8]，成功地將廣義周期性的理念引入到曲線坐標系和柱坐標系下，例如：在曲線坐標系下構建出廣義聲子晶體曲梁結構；在柱坐標系下構建出一維廣義聲子晶體薄圓板以及壓電型廣義聲子晶體薄圓板。需要指出的是，Torrent等[9]提出了一類徑向波晶體概念；Li等[10]和Ma等[11]構造了兩類徑向聲子晶體，針對Lamb波在其中的傳播特性進行了研究，并指出這類結構可用于結構的探傷；Ye等[12]對兩種流體組成的復合球殼對中心點聲源的透射系數與反射系數進行了研究，但是并沒有針對固體情況進行探索，也未揭示出帶隙的產生機理。

在以上研究的基礎上，本文進一步構建了柱坐標系下具有徑向周期性的一維徑向聲子晶體柱殼。柱殼的振動與聲輻射問題一直是結構聲學的重點，文獻[13-18]分別采用解析法和數值法討論了單雙層圓柱殼的振動與聲輻射性能，這些研究主要集中在圓柱殼結構受簡諧力作用下的振動與聲輻射，而對于內部聲源作用下的周期圓柱殼的外場聲輻射問題的研究較少。隨著靜音設備和減振隔振技術的發展，機械力引起的噪聲得到了有效的控制，使得內部聲激勵殼體的振動及聲輻射的研究更加重要。為此我們針對聲波在徑向聲子晶體柱殼內的軸對稱傳播問題展開研究，力圖發現一些有意義的現象并研究其產生機理，以期能夠為此類結構的減振降噪提供一種新的原理和技術途徑。

1 理論分析

圖1為我們所構建的系統結構簡圖。圖中，徑向聲子晶體柱殼是由兩種不同彈性常數和密度的固體介質材料A和B在r方向上交替嵌套排列形成的一維柱狀周期結構；聲波入射空間和出射空間流體介質區域分別用I和II來表示。

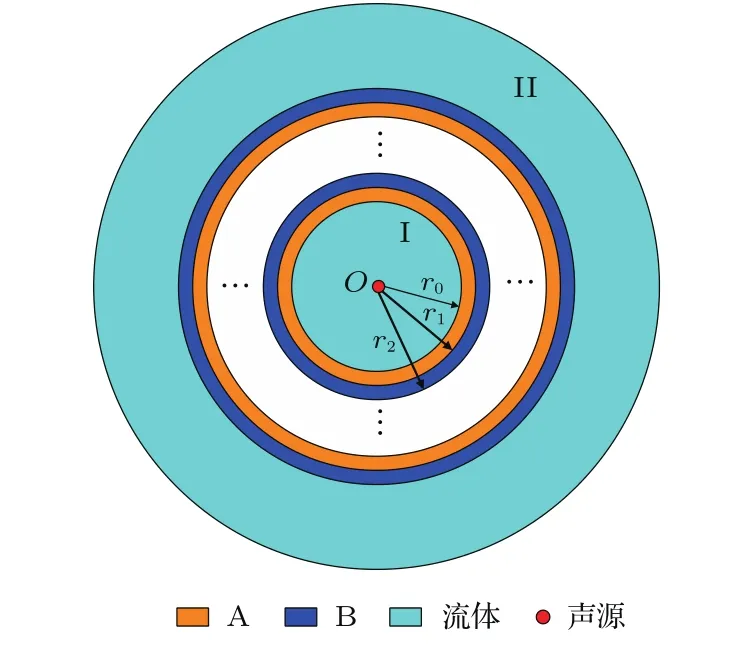
圖1 線聲源和徑向聲子晶體柱殼結構簡圖Fig.1 Schematic diagram of the line source and cylindrical shell of radial phononic crystals

在線聲源激勵下，能量的傳輸途徑為聲源-內部流體介質-徑向聲子晶體柱殼-外部流體介質，故柱殼內外流體介質存在聲輻射，而殼體將產生振動，需對聲場和結構場分別進行分析。

1.1 聲場方程

線聲源作用下，區域I內入射波場的聲壓表達式為

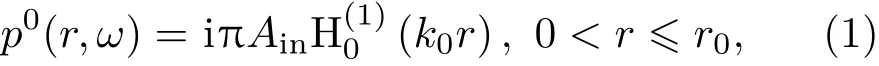
其中，Ain為待定系數，為漢克爾函數，k0=ω/c0，c0代表聲腔內流體介質的聲速。

由于流體介質與徑向聲子晶體的阻抗特性不同，在區域I內必然還存在反射波。反射波場聲壓的表達式為

其中，R0為待定系數，J0為貝塞爾函數。

故內部聲腔總的聲壓表達式為

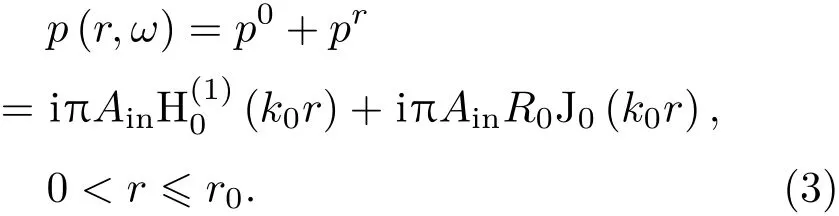
在區域II(r>r2N,N為總周期數)存在著透射聲場，透射波的聲壓表達式為

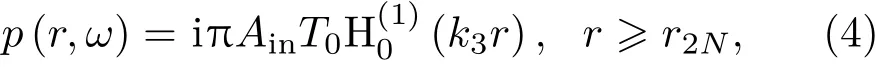
其中，T0為待定系數，k3=ω/c3，c3為外部流體介質的聲速。

區域I、II聲場的質點振動速度表達式為[19]

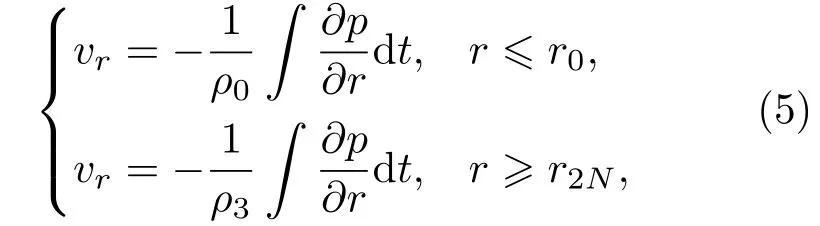
其中，ρ0、ρ3分別代表柱殼內外流體的密度。

聯立式(1)、式(2)、式(4)，推導出聲壓透射TR和反射系數RF表達式為

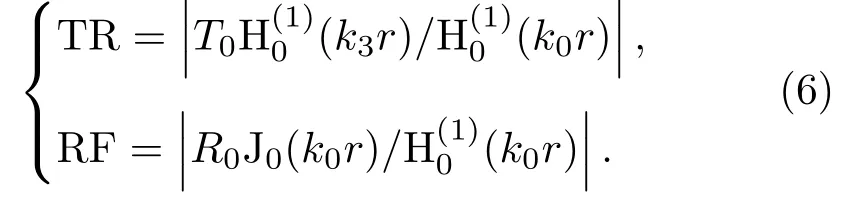
隔聲量的一般通式可表示為

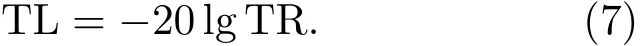
聯立式(6)、式(7)即可推導出徑向聲子晶體柱殼隔聲量的具體表達式。

徑向聲子晶體柱殼內外側的聲壓級之差為

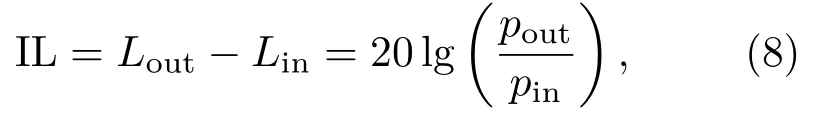
其中，IL為聲壓級之差，Lout、Lin分別表示柱殼內外層的聲壓級。式(8)中，

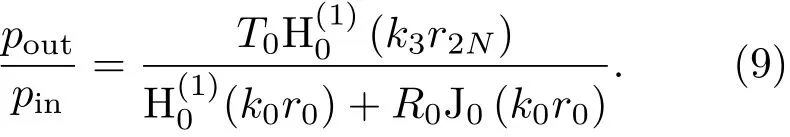
1.2 結構場方程

在中心線聲源激勵下，彈性固體中只存在縱波。縱波在徑向聲子晶體柱殼中傳播的控制方程表示為[20]

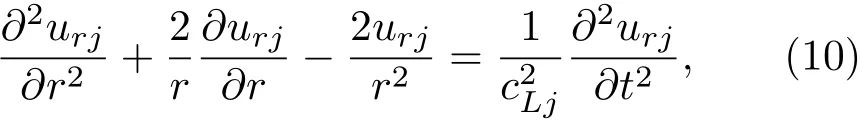
式(10)中，urj代表徑向位移，cLj=為縱波的波速，λ和μ為拉梅常數，j=1,2代表任意組元中的子層1和子層2。

方程(10)的通解表示為

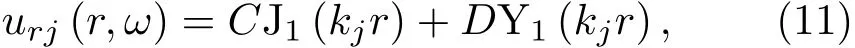
其中，C、D為待定系數，J1、Y1分別表示一階第一類和第二類柱貝塞爾函數，kj為波數。

徑向應力表示為

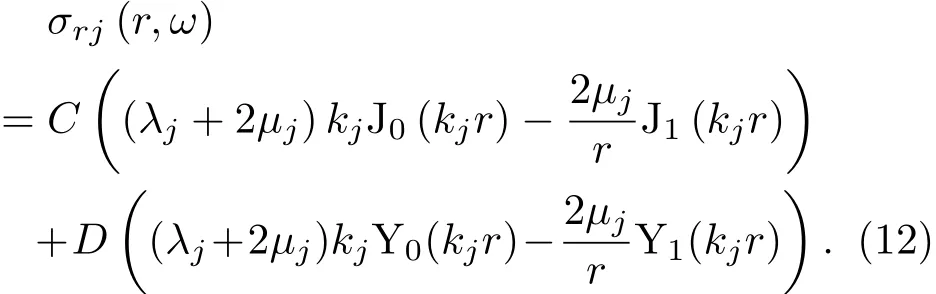
式(11)、式(12)即為徑向聲子晶體柱殼在聲波激勵下徑向位移與應力的表達式。

本文重點關注的是反射聲場和透射聲場的大小及其分布情況，而采用力學狀態向量傳遞矩陣法，可以直接將內外聲場與結構場聯立起來求解透射系數和反射系數，進而能夠消除求解結構場各周期組元待定系數的復雜性。鑒于在之前的研究中詳細地推導了徑向波在徑向聲子晶體柱殼中由內向外傳播的力學狀態向量傳遞矩陣，本文在計算過程中直接引用相關方程[21]。

求解透射系數以及反射系數的前提需先求出未知系數R0和T0，應用聲固耦合協調條件來進行求解，即在柱殼內壁(r0)和柱殼外壁(r2N)界面處固體和流體的法向振速相等、固體的法向正應力與流體的聲壓相等：

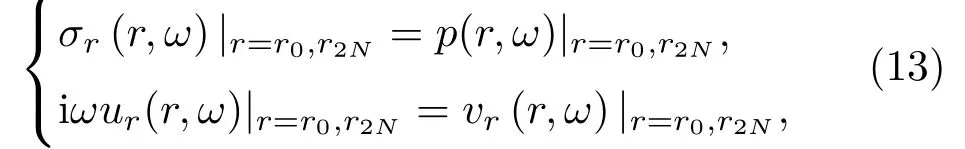
求解式(13)即可求出系數R0和T0。

2 數值計算和有限元仿真

為了能夠說明問題的本質，我們進行一些數值算例分析。假定柱殼內外的流體介質為理想狀態下的水(ρ0/3=1000 kg/m3,c0/3=1480 m/s)；柱殼本體結構的材料參數如表1所示。

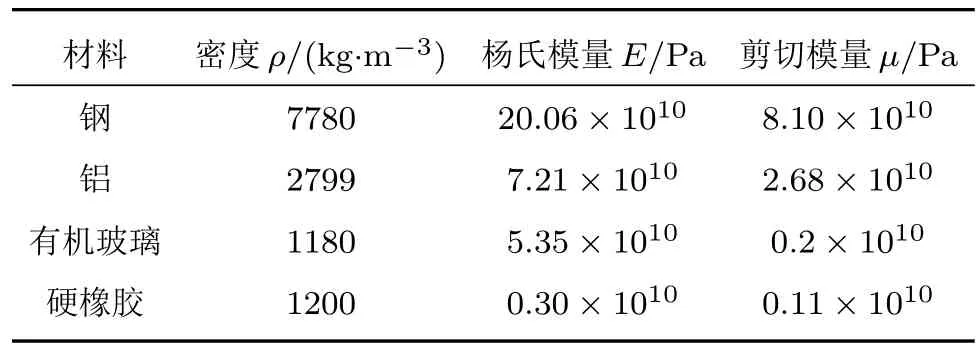
表1 線彈性材料參數Table 1 Linear elastic material parameters

2.1 單一材質柱殼隔聲性能分析

2.1.1 殼體厚度(d)

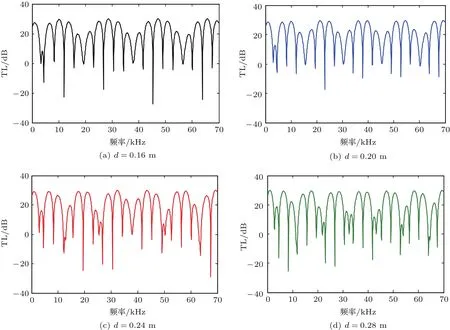
圖2 聲波在不同厚度鋼質柱殼中傳播時隔聲量頻響曲線Fig.2 The sound insulation frequency response curve when acoustic waves propagate in steel shells with dif f erent thicknesses

首先分析殼體的厚度對隔聲性能的影響。圖2給出了在聲腔尺寸r0=0.2 m情況下，聲波在不同厚度(d)鋼質柱殼中傳播時隔聲量頻響曲線。觀察圖2我們可以發現，這四條隔聲量頻響曲線均存在較為密集的共振峰和節點，當聲波頻率接近于TL曲線節點對應頻率時，聲波得到了一定程度上的抑制；相反，當入射聲波頻率接近共振峰對應頻率時，該結構顯然并沒有起到隔聲的效果。此外，由于聲波多重反射的相干性，四條曲線表現出一定的周期性，其隨著柱殼厚度d的增加，周期數目增多，周期變小。

縱觀全圖，就隔聲效果而言，隨著d的增加，TL曲線的數值并沒有顯著變化，在低頻范圍內(0.1 kHz～2 kHz)TL的值有略微增加，而在高頻處TL的最大值穩定在30 dB左右，顯然單純地增加柱殼厚度能夠對低頻聲波進一步產生一定程度的抑制作用。

2.1.2 聲腔尺寸(r0)

將柱殼厚度統一設定為0.16 m，分別對聲腔尺寸為0.2 m、0.5 m、1.0 m和2.0 m的四種鋼質柱殼進行數值計算，相應的隔聲量頻響曲線如圖3所示。對比圖3可以發現，隨著聲腔尺寸的擴大，隔聲量頻響曲線的包絡線周期數目是不變的，但其峰谷數目增多。這表明聲腔尺寸影響峰谷的位置以及疏密程度，而殼體厚度控制著包絡線的數目。

對于聲腔尺寸的增大意味著波陣面的擴大，文獻[7]已經證明了波陣面對近場波的作用較為明顯，而對遠場波的影響較小，所以單材質柱殼會表現出隨著聲腔尺寸的增大，低頻聲波的衰減逐漸越小，而高頻聲波的衰減量幾乎沒有變化這一現象。

2.1.3 結構材料

由隔聲質量作用定律可知，結構材料特性阻抗的不同，將導致不同材質殼體的隔聲性能也不相同。圖4給出了同一厚度(d=0.16 m)和聲腔尺寸(r0=0.2 m)下，不同材質柱殼隔聲量的頻響曲線圖。明顯可以發現，除部分共振峰位置外，單質柱殼表現出特性阻抗越大，隔聲能力越強。

2.2 徑向聲子晶體柱殼的隔聲特性分析

針對由鋼(A)、硬橡膠(B)兩種材料組成的徑向聲子晶體柱殼進行隔聲特性分析，組元及聲腔的結構尺寸參數如表2所示。為了能夠說明問題同時便于和單質柱殼隔聲能力進行對比，此處，我們針對四周期的徑向聲子晶體柱殼模型進行分析。

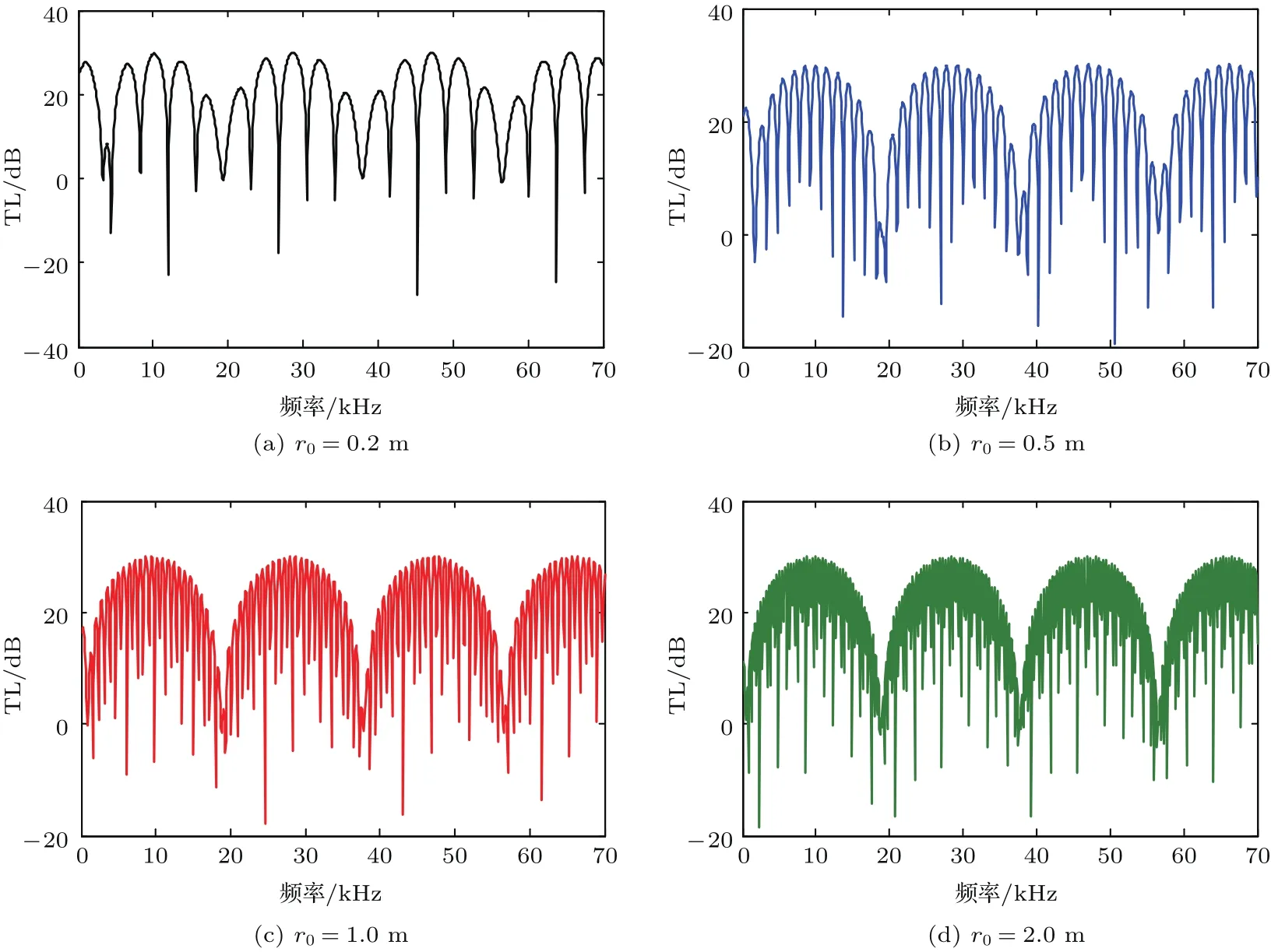
圖3 不同聲腔尺寸殼體的隔聲量曲線Fig.3 The sound insulation curve of the shells with dif f erent acoustic cavities

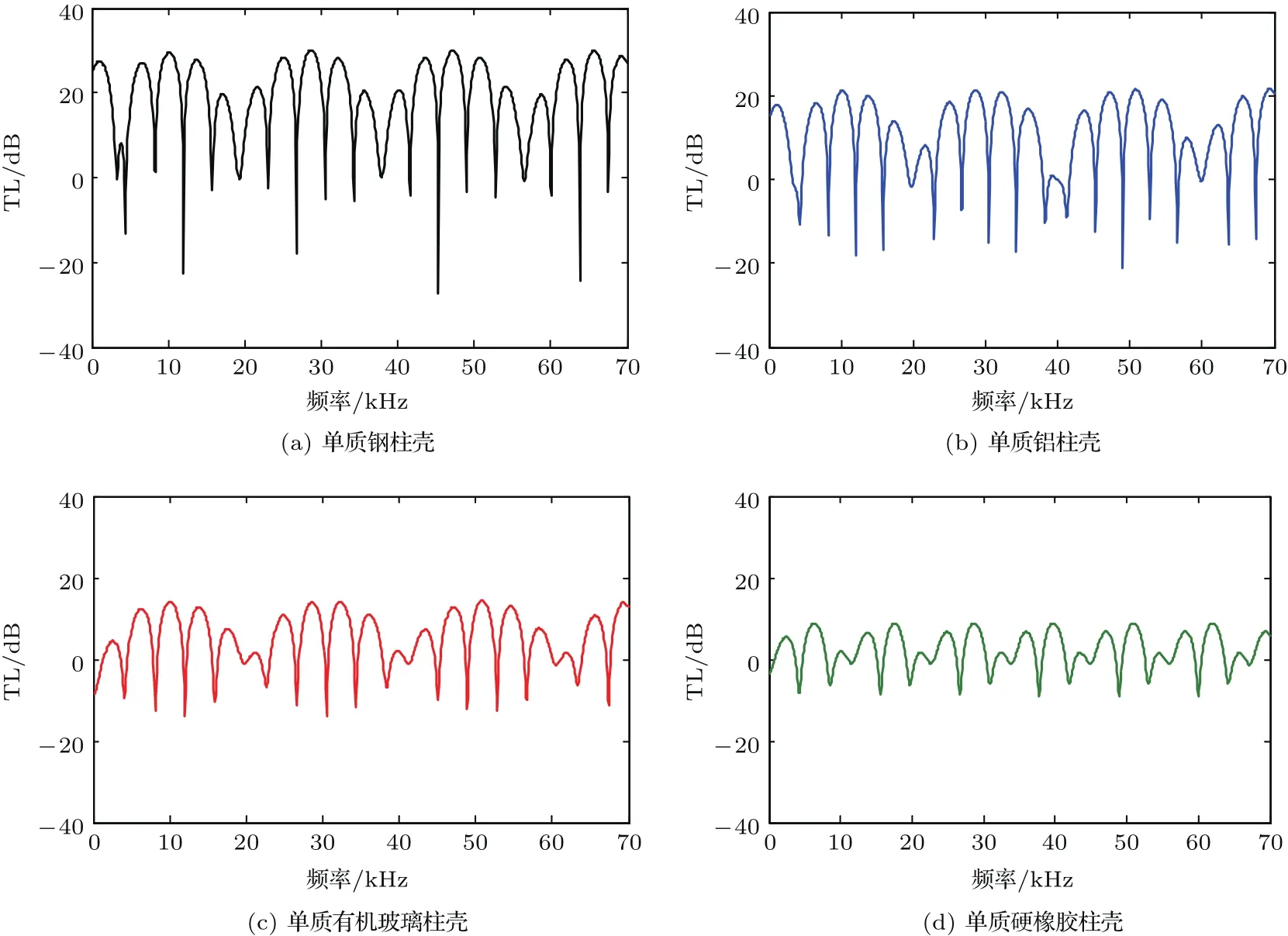
圖4 不同材料殼體的隔聲量曲線Fig.4 The sound insulation curve of dif f erent material shells

表2 結構尺寸參數Table 2 Structural dimension parameters

根據第1節的理論分析，對徑向聲子晶體柱殼的透射系數和隔聲量進行計算，其計算結果如圖5所示。

由圖5可知，徑向聲子晶體柱殼在中高頻域(13.2 kHz～57.1 kHz)內均存在一個明顯的聲波帶隙包絡線。在聲波帶隙范圍內，透射系數曲線的數值都小于1，隔聲量曲線的數值都在0 dB以上，最大隔聲量為86.51 dB，明顯高于單質鋼和硬橡膠柱殼，說明聲波得到有效的抑制；而在低頻范圍內徑向聲子晶體與單一材質殼體的隔聲量并沒有顯著的區別。

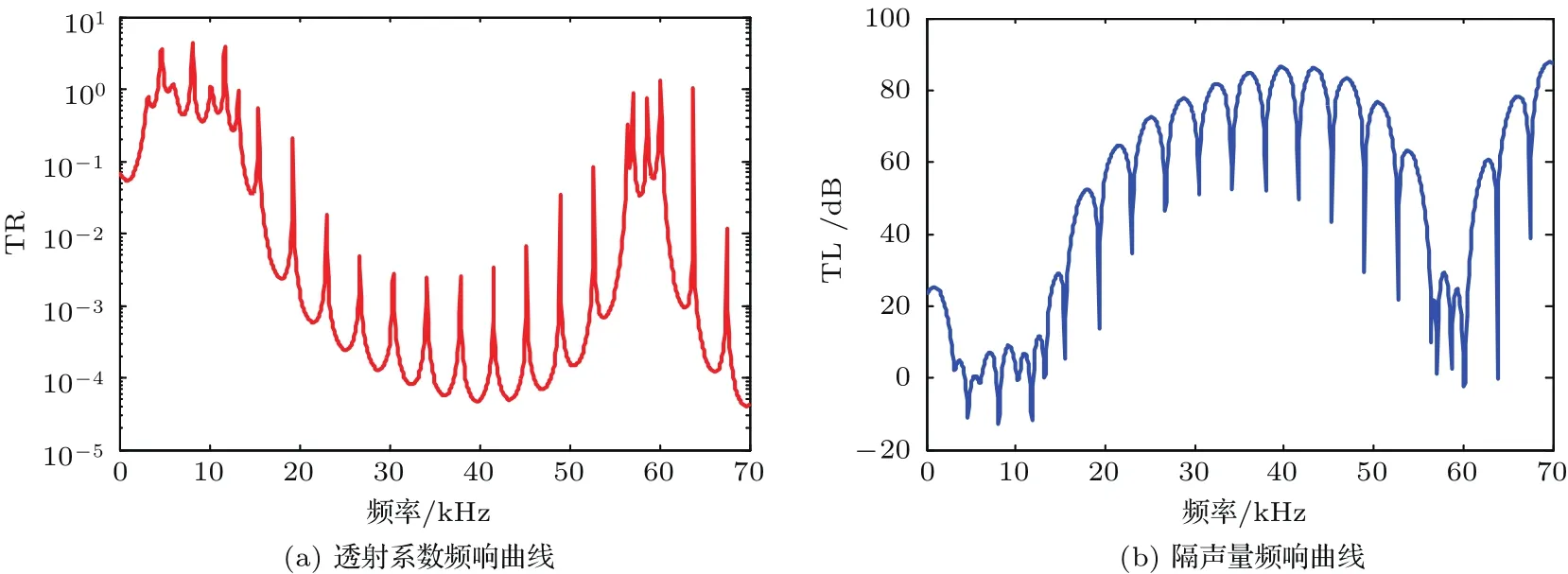
圖5 徑向聲子晶體柱殼的透射系數和隔聲量頻響曲線Fig.5 Transmission coefficient and sound insulation frequency response curve of cylindrical shell of radial phononic crystal

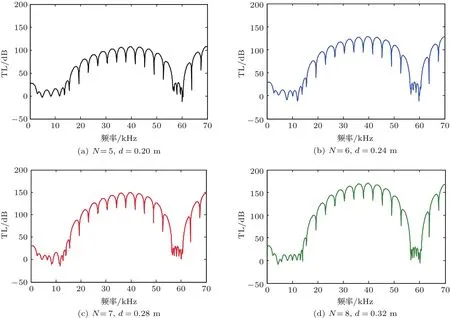
圖6 不同周期數下徑向聲子晶體柱殼的隔聲量頻響曲線Fig.6 The sound insulation frequency response curve of cylindrical shell of radial phononic crystals in dif f erent cycles

由質量定律可知，增加單一材質殼體的壁厚來提高隔聲量并不是一種高效的手段，在第2.1節針對單一材質柱殼隔聲性能進行了分析，此處為了便于對比，圖6給出了與單質鋼柱殼相同厚度的徑向聲子晶體柱殼的隔聲量曲線。可以看到，隨著殼體總周期數目N(相當于柱殼的壁厚)的增加，中高頻處帶隙內的隔聲量顯著增加，而在0.1 kHz處的隔聲量略有增加。由此可見，徑向聲子晶體柱殼在帶隙范圍內表現出來的特性突破了聲學中質量定律的限制，即可以實現厚度增加一倍，隔聲量增加一倍的效果。

2.3 有限元仿真驗證

采用COMSOL 5.3聲固耦合模塊對四周期徑向聲子晶體柱殼隔聲性能進行有限元仿真驗證。由于軟件不便于拾取徑向聲子晶體柱殼的隔聲量，而可以拾取柱殼內外聲場的聲壓級，其具體數值由聲源功率所調控，考慮到僅計算內聲場或外聲場的聲壓級曲線并不能體現徑向聲子晶體柱殼的隔聲特性，所以此處針對徑向聲子晶體柱殼內外聲場與結構場接觸面的聲壓級之差進行計算，同時根據式(8)給出數值計算結果，并將兩者計算結果進行對比，從而可以驗證理論分析的正確性，計算結果如圖7所示。

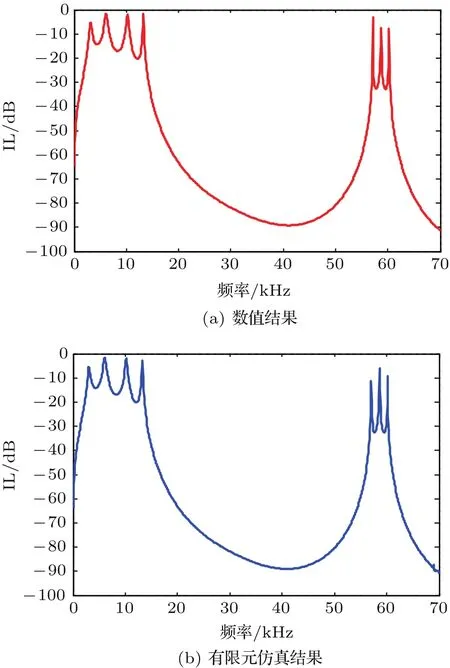
圖7 徑向聲子晶體柱殼的內外聲壓級之差頻響曲線Fig.7 The dif f erence frequency response curve of the inner and outer sound pressure level of cylindrical shell of radial phononic crystals

對比兩條頻響曲線可知，就帶隙位置以及衰減量而言，有限元仿真結果與數值結果幾乎完全一致，從而驗證了理論分析和數值計算相關結論的正確性。

3 流體介質參數對TL影響規律

隔聲量的表達式與內外聲場流體介質以及徑向聲子晶體結構場的本體結構參數有關。目前對于本體結構中材料和結構參數對聲子晶體彈性波帶隙的影響研究很多，故在本節中，主要針對聲場流體介質參數對隔聲量的影響進行分析。表3給出了部分常用流體介質的聲學常數。

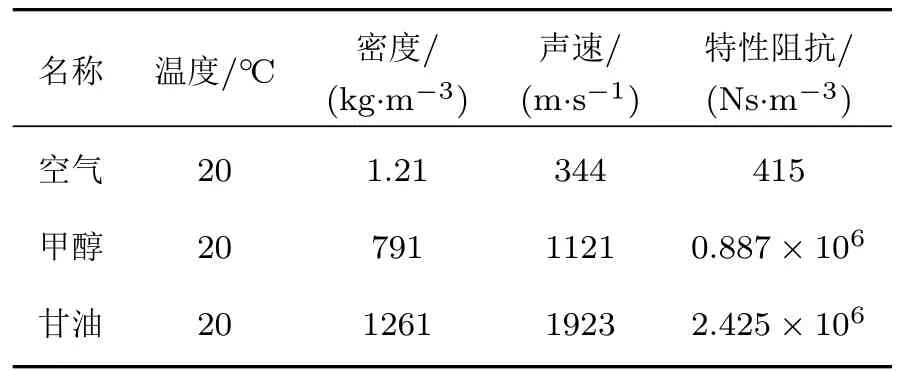
表3 流體介質的聲學常數表Table 3 Acoustic constants of the f l uid medium

3.1 內聲場流體介質特性阻抗

假定徑向聲子晶體柱殼的本體結構和外聲場流體介質(理想狀態下的流體水)固定不變，通過改變內部流體介質的特性阻抗來探索隔聲量頻響曲線的變化規律。

當內部聲場介質的阻抗很小時，隔聲量頻響曲線峰谷相對較多，隨著阻抗的增加，其數量也逐漸減少。圖8及圖5(b)表現出一個共同點，即聲波帶隙的位置完全相同，表明聲波帶隙的位置完全是由徑向聲子晶體本體結構所調控。

3.2 外聲場流體介質特性阻抗

接下來，假定殼體內腔的流體介質為水，徑向聲子晶體本體結構不變，改變殼體外部聲場流體的特性阻抗參數，使外部聲場介質的特性阻抗逐漸增大，研究隔聲量曲線的變化規律。

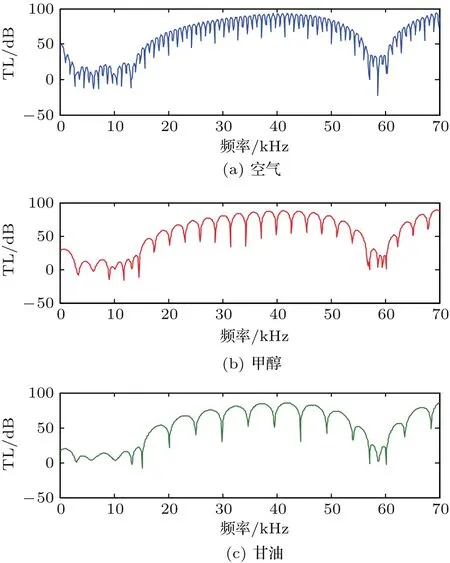
圖8 徑向聲子晶體柱殼內腔流體參數對隔聲量的影響Fig.8 The inf l uence of internal f l uid parameters of cylindrical shell of radial phononic crystal on the sound insulation

由圖9可以看出，在整個頻率區間內曲線的疏密程度幾乎是不變的，同時聲波帶隙的位置也是一致的。然而在圖9(a)中，隔聲量曲線在帶隙范圍內 (30 kHz附近處)存在明顯的共振峰，而其他曲線并沒有出現這一現象，通過進一步分析可知此共振峰位置正對應于表面波模態頻率，即出現表面局域態現象。而彈性波帶隙內表面局域態現象出現與否，與聲子晶體材料的排列順序有關[22?23]。此處，我們進一步討論探索聲波帶隙內表面局域態現象的出現與徑向聲子晶體材料(軟/硬)和內外流體介質(輕/重流體)的排列順序的關系。通過多組數值計算，得出了表面局域態現象的出現規律，如表4所示。

首先，當內外流體介質采用輕流體排列時，隔聲量頻響曲線帶隙范圍定會出現表面局域態現象，相反，采用重流體排列時，則不會出現；當內外流體介質與徑向聲子晶體組元采用輕/重流體-軟/硬材料或重/輕流體-硬/軟材料組合排列時，會出現表面局域態現象，相反則不會出現。結果表明，隔聲量頻響曲線是否會在表面波模態對應頻率處出現表面局域態現象，不僅與徑向聲子晶體柱殼組元材料排列順序(即自由表面層的波速)有關，同時還受內外聲場介質的特性阻抗影響。

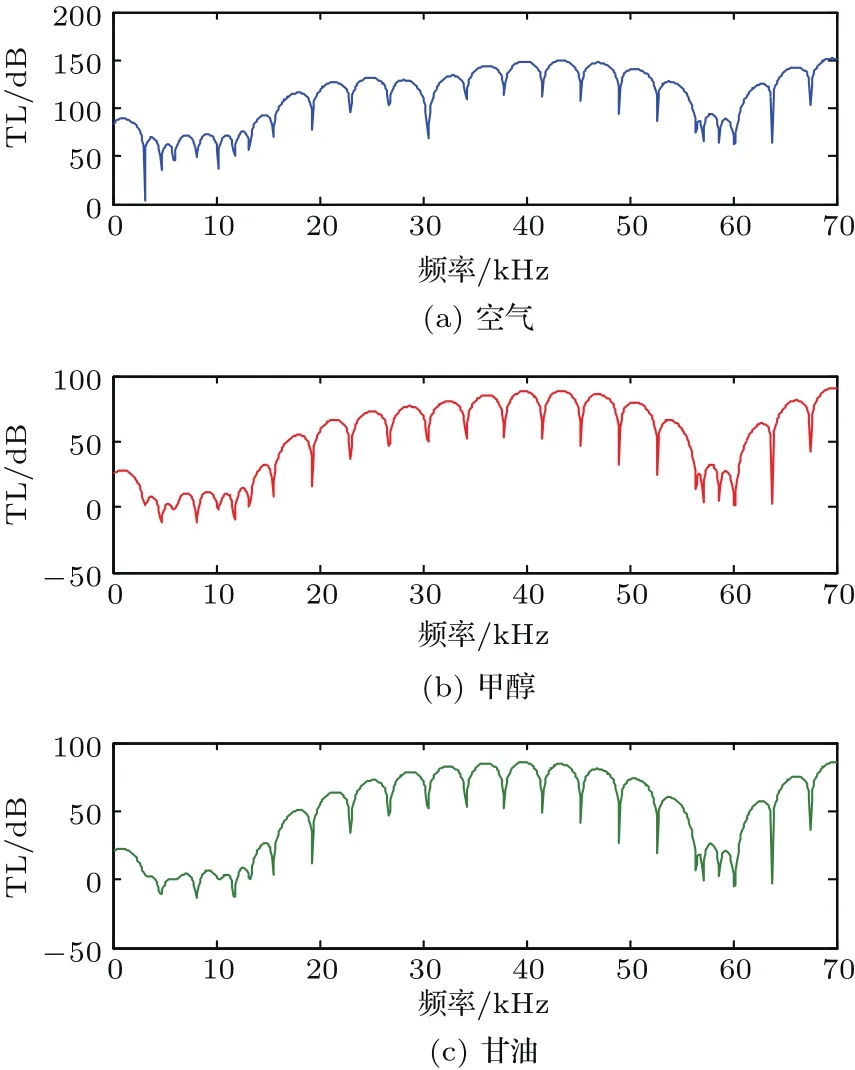
圖9 徑向聲子晶體柱殼外部聲場流體參數對隔聲量的影響Fig.9 The inf l uence of external acoustic f i eld f l uid parameters of cylindrical shell of radial phononic crystals on the sound insulation

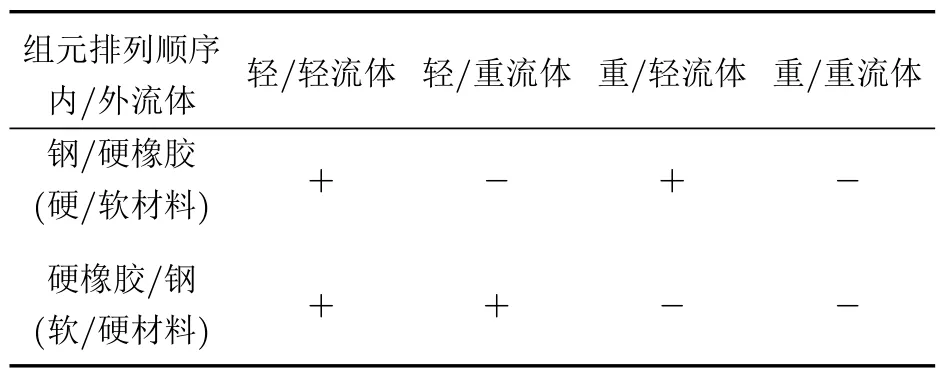
表4 表面局域態現象(+代表存在，?代表不存在)Table 4 The surface localized modes(+represents existence,?represents nonexistence)

4 結論

本文構建了徑向聲子晶體柱殼的模型。采用力學狀態向量傳遞矩陣法將內外聲場與結構場的力學量相結合，系統地研究了在中心線聲源激勵下聲波在徑向聲子晶體柱殼中的傳播特性，并與單一材質柱殼中的傳播規律進行對比分析；然后借助有限元方法對數值計算結果進行了驗證；最后重點討論內外聲場流體介質對隔聲量的影響規律。研究表明：

(1)聲波在徑向聲子晶體柱殼傳播過程中，聲波帶隙的出現能有效地抑制聲波由內向外的傳播；此外，其在帶隙范圍內表現出來的隔聲特性已經突破聲學中的質量定律的限制，當徑向聲子晶體柱殼的壁厚增加一倍時，帶隙范圍內的隔聲量數值顯著增加近一倍。

(2)徑向聲子晶體內外聲場流體參數對隔聲量頻響曲線峰谷的疏密程度會產生影響，但并不影響聲波帶隙的位置，帶隙的位置是由徑向聲子晶體本體結構所決定。此外，隔聲量頻響曲線是否會在表面波模態對應頻率處出現表面局域態現象，不僅僅與徑向聲子晶體柱殼組元材料排列順序(即自由表面層的波速)有關，同時還要受內外聲場介質的特性阻抗的制約，即由內外聲場和結構場介質共同決定。

本文的研究對實際工程應用具有一定的指導性，同時也對隔聲問題提供一種新的解決途徑，拓寬了減振降噪思路。例如，通過合理設計徑向聲子晶體的材料和結構參數，可以構造出具有不同隔聲性能的隔聲罩，若進一步結合現有隔聲罩原理(如附著各類吸聲材料)進行集成，那么極有可能獲得性能更為優異的新型隔聲罩。