3-RPS并聯機構神經網絡滑模變結構控制

王 欣,陳振威

(1.東莞職業技術學院 電子工程系,廣東 東莞 523808; 2.東莞成電金盤軟件技術有限公司 技術部,廣東 東莞 523000)

并聯機構具有多運動空間維度、運動精度高、結構剛度大等特點,因而廣泛應用于生物工程、微納制造及裝備、并聯機床等高精密領域[1].隨著并聯機構宏觀控制與微觀控制技術相結合的研究不斷深入,并聯機構的控制系統設計越來越受到學者們的關注,但是并聯機構是一個高耦合、強非線性的多變量控制系統,如何降低并聯機構的軌跡跟蹤誤差逐漸成為研究的重點[2].文獻[3]基于一種空間3自由度并聯機構的運動學和動力學模型,采用自適應反演滑模變結構控制研究了機構的穩定誤差和穩定時間.文獻[4]以6-PUS并聯機構為研究對象,采用簡化模型和線性反饋求解的方法，設計了一種神經網絡PID控制器,對機構的啟動力矩、穩態誤差和抗干擾性進行了仿真.文獻[5]通過Matlab軟件建立了3-RPS并聯機構的仿真模型,比較了PID和滑模變結構控制器在添加干擾條件下的軌跡跟蹤誤差.文獻[6]提出了一種基于6自由度并聯機構的模糊PID控制器,討論了控制系統的運動精度和動態響應.為了降低3-RPS并聯機構的軌跡跟蹤誤差,本文設計了一種徑向基函數(Radial Basis Function,RBF)神經網絡滑模變結構控制器,有效提高了機構的軌跡跟蹤精度.

1 3-PRS并聯機構模型

1.1 機構特征

3-RPS并聯機構主要包括對稱的3條支鏈、動平臺和定平臺3部分結構,每一部分支鏈含有3個運動副,即1個轉動副(R)、1個移動副(P)和1個球副(S).機構通過R副與定平臺相連接,S副與定平臺相連接,并在R副與S副間通過P副進行串聯,R副是機構的驅動副,為機構提供動力.分別在機構定平臺等邊△abc和動平臺等邊△ABC的中心點,建立機構的靜坐標系O-XYZ和動坐標系o-xyz,等邊△abc和△ABC的邊長分別為m和n,各桿件的長度均為l,與定平臺的夾角為φi(i=1,2,3).3-RPS并聯機構模型如圖1所示.

圖1 3-RPS并聯機構模型Fig.1 Model of 3-RPS parallel robot

1.2 運動特性分析

由螺旋理論可知,研究并聯機構的運動特性,首先需要分析每條支鏈對動平臺產生的運動螺旋,并綜合分析機構所受的約束螺旋類型,以分析出機構的運動特性[7].由于3-RPS并聯機構是對稱機構,因此,只需研究機構的一條支鏈的約束螺旋即可.取支鏈Bb為研究對象,支鏈轉動副B的軸線方向為繞Y軸轉動,則轉動副B的運動螺旋為

移動副的運動螺旋為

球副B可以等價為3個轉動副,假設其3個轉動副的軸線方向分別為繞X,Y和Z軸的轉動,則球副B的運動螺旋為

綜上,支鏈Bb的運動螺旋系為

由于機構運動螺旋與約束螺旋的互易積為0,可得機構的約束螺旋系為

(1)

根據式(1)和并聯機構的對稱性可得,機構動平臺總共受到3個約束力的作用,方向與對應基面上轉動副的軸線方向一致.因機構在初始狀態時動定平臺平行,所以該3個約束力的線矢共面.該3個不匯交的約束力共面線矢是線性無關的,則約束了機構動平臺沿X,Y軸的移動和繞Z軸的轉動.因此,3-RPS并聯機構可實現繞X,Y軸的轉動和沿Z軸的移動.

1.3 機構動力學模型

采用拉格朗日法(Lagrange法,L法)研究并聯機構動力學特性時,從動能和勢能的角度進行分析,不用考慮機構角速度和加速度的問題,求解較簡便.因此,采用L法描述的3-RPS并聯機構二階微分方程為[8]

(2)

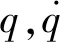
2 神經網絡滑模控制律

2.1 控制器的設計

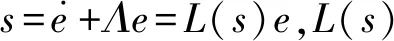
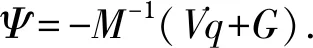
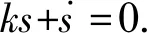
在實際工程運用過程中,由于摩擦、振動等不確定因素的存在,不可能精確地建立機構的動力學模型,所以機構模型不可避免地存在未建模部分,且存在外界干擾的作用,故F=0是不成立的.因此,上述的控制律τc所控制的機構閉環系統不具有魯棒穩定性.基于上述控制律的缺陷,本文采用RBF神經網絡控制律τR來逼近控制律τc,其結構原理模型如圖2所示.RBF神經網絡算法具有強大的在線識別、非線性系統映射和自學習功能,可實現對系統模型不確定參數的在線估計和對外界干擾的補償,從而有效提高了滑模控制器的魯棒性.

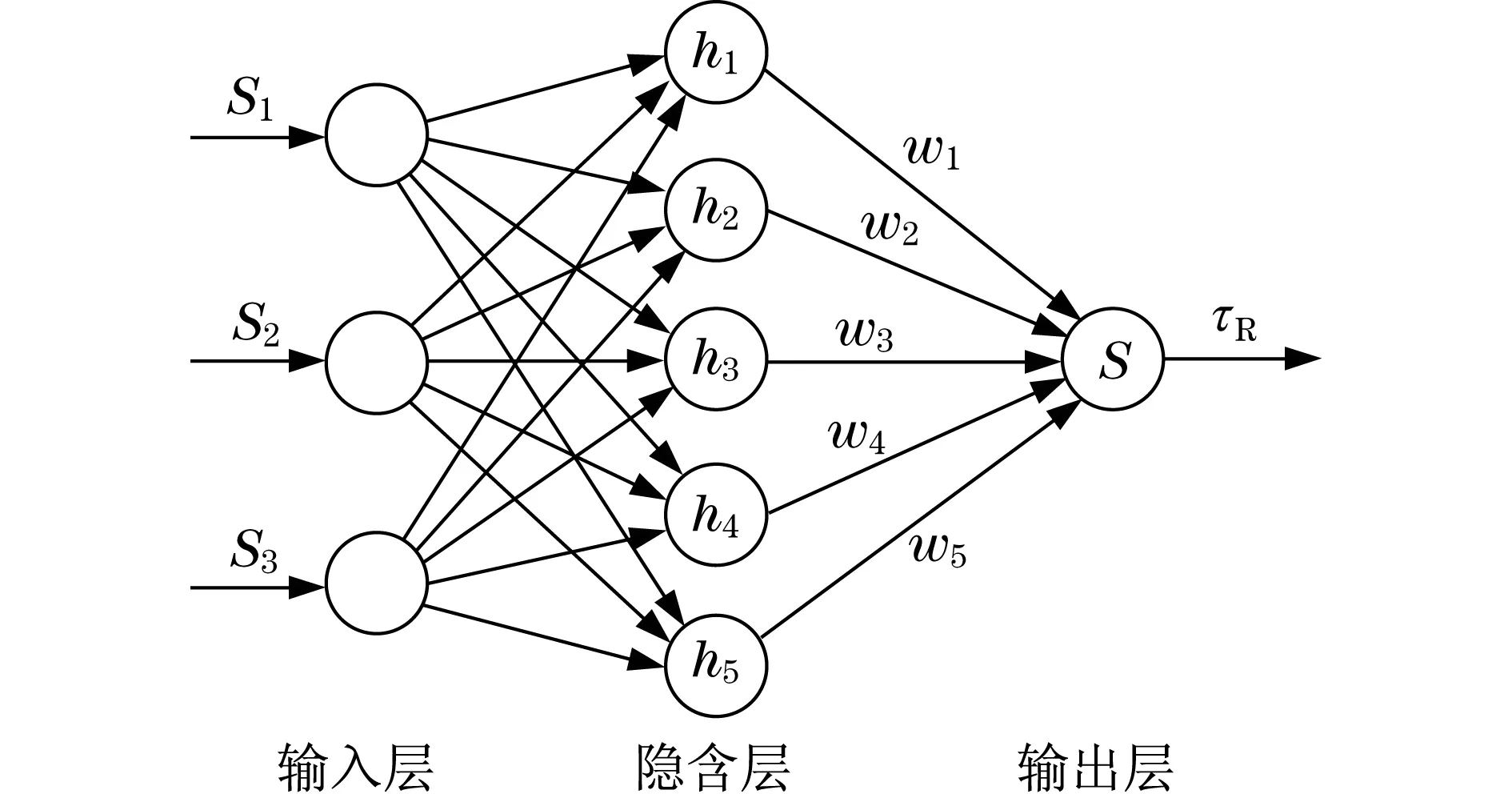
圖2 RBF結構原理模型Fig.2 Model of RBF structure principle

通過引入RBF神經網絡算法,則控制律τR可表示為

(3)

式中:τa為有界項;τb為魯棒項.

2.2 有界項分析

將式(3)代入式(2)的變形表達式可化簡為

構造的Lyapunov函數為

對上式求導可得

若存在已知函數|f|和常數|d|,使不等式|Fi|≤f,|Di|≤d成立.選取有界項為

(4)

式中:Γ(t)為關于Me的分段函數;Kai=|τRi|+|τsi|+d+f.

2.3 魯棒項分析

對上式求導可得

式中:ω1=ω+F為機構建模偏差.

(5)

式中:λmin(M)為矩陣M的最小特征值.

3 控制仿真

圖3 神經網絡控制示意圖Fig.3 Schematic diagram of neural network

圖4 機構X軸方向的跟蹤誤差曲線Fig.4 Tracking error curve of mechanism’s X axis

由機構的跟蹤誤差曲線可知,機構在滑模變結構和神經網絡滑模變結構控制策略下都能達到一定的穩定跟蹤精度,兩種控制方式在開始的1 s內,跟蹤誤差都比較大,這可能與機構啟動時需克服摩擦阻力有關.但是隨著神經網絡控制的逼近運算,神經網絡滑模變結構控制的誤差逐漸趨近于0,而滑模變結構控制的誤差還是較大,說明神經網絡滑模變結構的控制效果更好,在響應速度和穩定性方面較優.

圖5 機構Y軸方向的跟蹤誤差曲線Fig.5 Trackingerror curve of mechanism’s Y axis

圖6 機構Z軸方向的跟蹤誤差曲線Fig.6 Tracking error curve of mechanism’s Z axis

4 結論

通過分析3-RPS并聯機構的運動學特征和動力學方程,為控制系統的設計提供了控制對象.在滑模變結構控制的基礎上,引入RBF神經網絡控制律,研究了機構在兩種不同控制方式下的誤差曲線.結果表明:基于RBF神經網絡滑模變結構的閉環控制系統,其軌跡跟蹤誤差更小,自適應魯棒性更好,在工程實踐方面具有重要的參考價值.