基于自適應步長RRT的雙機器人協同路徑規劃
李 洋 徐 達 周 誠
(陸軍裝甲兵學院兵器與控制系, 北京 100072)
0 引言
RRT作為具有概率完備性的規劃方法[1-4]廣泛應用于機器人的路徑規劃。該方法省略了在C-space(構型空間)中建立障礙物模型的過程,只需在節點處進行碰撞檢測,其運行速度快,對于高維空間的路徑規劃優勢更加明顯。目前,國內外學者針對RRT提出了多種改進方法,LIN等[5]提出了一種自適應步長RRT,該方法可根據障礙物自動調整隨機樹的生長方向,可快速生成避障路徑。WANG等[6]提出了變步長RRT方法,在隨機樹的生長過程中,加入了貪婪思想,使隨機樹以固定步長增量盡可能生長,加快了RRT算法的收斂速度,但無法控制在W-space(工作空間)中的步長大小。文獻[7-10]提出了自適應維度RRT,通過降低C-space的局部維度,提高算法的運行速度,但該方法沒有考慮節點之間的碰撞問題,無法保證碰撞檢測的有效性。劉成菊等[11]將勢函數引入到RRT算法中,減少了RRT算法的隨機性,在局部搜索過程中具有良好的避障效果。
目前,RRT及其改進方法的相關研究主要集中在移動機器人的路徑規劃,在雙機器人的協同路徑規劃方面,RRT相關應用較少。對于高維空間的運動規劃,RRT方法雖然省去了在C-space中建立障礙物模型的過程,但只在節點處進行碰撞檢測難以保證其有效性[12-15];利用RRT進行雙機器人協同路徑規劃時,在每個節點處兩個機器人末端執行器的相對位置必須保持固定[16-17],而雙機器人的隨機樹卻在各自的C-space中隨機生長,若要保持雙機器人之間的協調,需在不同的C-space中對機器人隨機樹的生長進行協調控制。
本文提出一種自適應步長RRT方法,通過構建C-space和W-space中步長的范數不等式,把隨機樹每一次生長產生的位移約束在給定范圍內,確保碰撞檢測的有效性,通過被動生長算法控制兩個機器人隨機樹的協調生長,完成雙機器人在W-space中的協調運動,以實現雙機器人協同路徑規劃。
1 雙機器人運動學模型建立與求解
1.1 雙機器人旋量模型
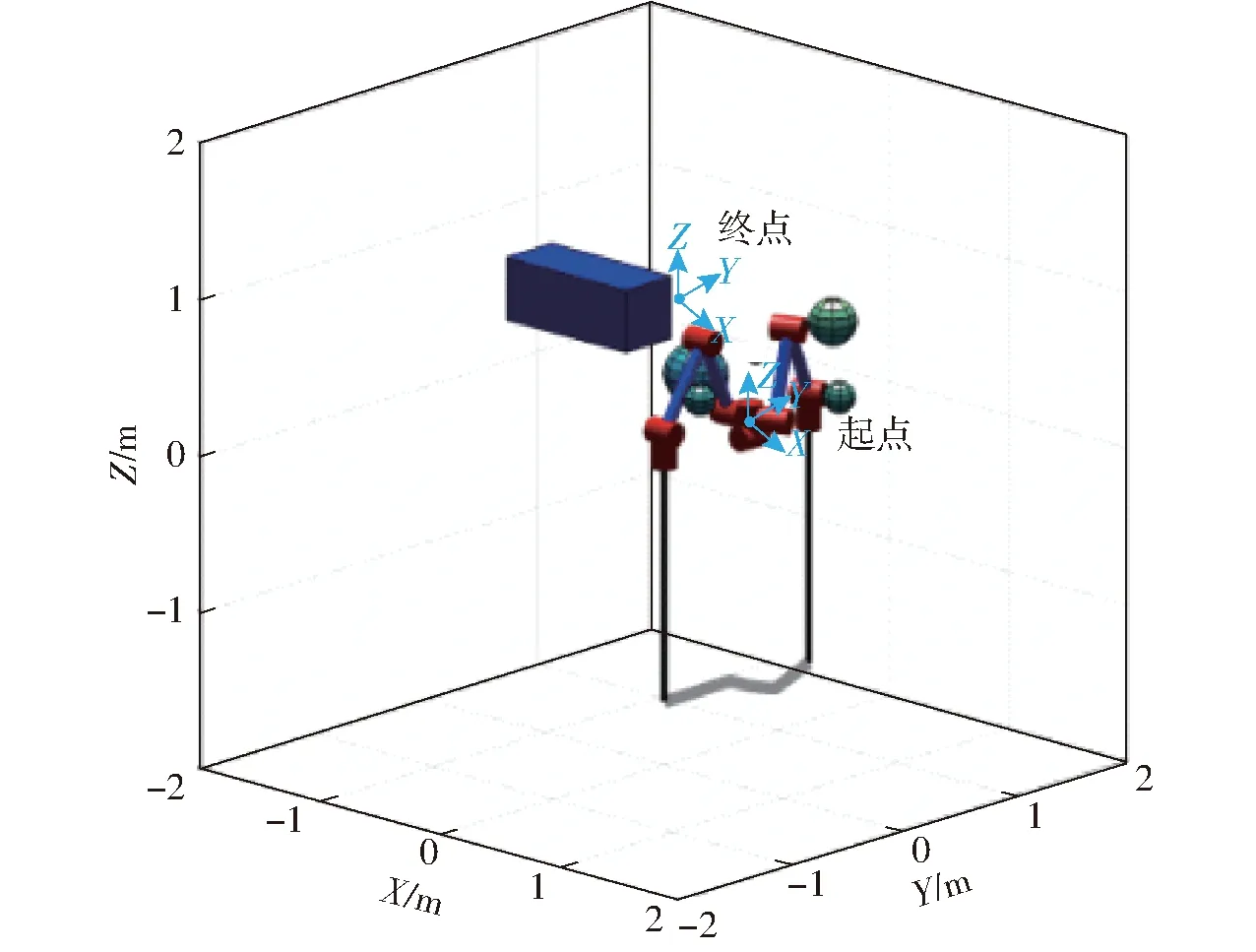
建立的雙機器人模型如圖1所示,雙機器人系統由機器人R1、R2組成,其基座坐標系分別為S1和S2,取S1為慣性坐標系,S2在慣性坐標系下的描述為
1S2=Rz(π)Tx(lx)Ty(ly)S2
(1)
其中
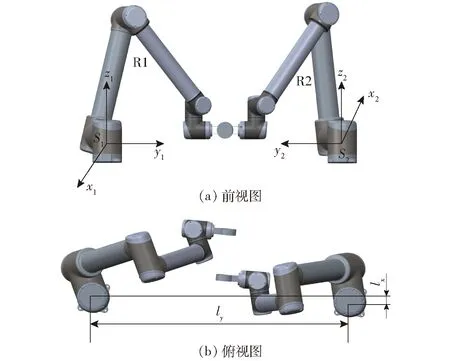
圖1 雙機器人模型Fig.1 Models of dual-robot
通過1S2可以將機器人R1和R2的運動學統一在慣性坐標系S1中表達,故只需在機器人R1、R2各自的基座坐標系下建立運動學模型即可。建立機器人R1的運動旋量模型,如圖2所示,R1的慣性坐標系S與基座坐標系重合,T為工具坐標系,關節1和5繞z軸方向旋轉,其余關節繞y軸方向旋轉,ri為各關節軸線所在位置,建立關節的運動旋量坐標
(2)
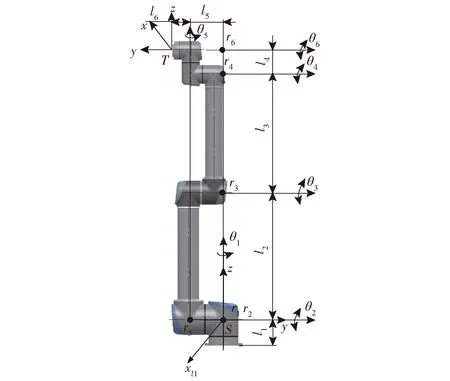
圖2 機器人R1的運動旋量模型Fig.2 Twist model of robot R1
將關節的旋量坐標映射為指數形式

1.2 正向運動學
根據串聯機器人的POE公式[18],計算R1的正向運動學方程
(3)
其中r11=-c6(s1s5-c1c5c234-c1s6s234)
r21=-c6(c1s5-s1c5c234-s1s6s234)
r31=-s6c234-c5c6s234
r12=-c5s1-c1s5c234r22=c1c5-s1c5c234
r32=s5s234r13=c1c6s234-s6(s1s5-c1c5c234)
r23=c6s1s234-s6(c1s5+s1c5c234)
r33=c6c234-c5s6s234
p1=l5s1+l2c1s2+l3(c1c2c3+c1s2c3)+
l4(c1c2c3s4+c1c2s3c4+c1s2c3c4-c1s2s3s4)
p2=-l5c1+l2s1s2+l3(s1c2s3+s1s2c3)+
l4(s1c2c3s4+s1c2s3c4+s1s2c3c4-s1s2s3s4)
p3=l1+l2c2+l3c23+l4c234
式中ci=cosθi,si=sinθi,cij=cos(θi+θj),sij=sin(θi+θj),下文同。
為實現雙機器人協同路徑規劃,須將機器人R1和R2的正向運動學統一在同一個坐標系下描述,由于機器人R1和R2具有相同的結構,所以機器人R2的正向運動學g2(θ)在S2中描述與g1(θ)相同,通過式(1)可將g2(θ)在慣性坐標系S下表述為
g2(θ)=1S2g1(θ)
(4)
1.3 逆向運動學
機器人R1和R2后3個關節的軸線不相交于一點,因此無法求解逆向運動學的解析解[19]。本文采用Newton-Raphson迭代法[20],首先給出一組估計解θ0和誤差Δ,通過多次迭代找到一組接近θ0且誤差小于Δ的數值解θt,θ0的選取在下文中會進行詳細的說明。
1.4 雅可比矩陣
雅可比矩陣定義了機器人單個關節速度對末端執行器速度的貢獻度,將機器人C-space中的關節速度映射到W-space的矩陣函數,是構建C-space和W-space中步長關系的關鍵。機器人R1末端執行器速度與關節速度的映射關系為
V=J(θ)θ′
(5)

(6)
式中θ′——關節速度
J(θ)——雅可比矩陣

機器人R1的6個關節皆為轉動副,因此有
(7)
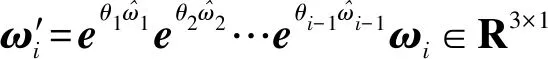
2 傳統RRT算法
采用固定步長RRT方法對機器人路徑進行規劃,需要在C-space中確定步長,對于多自由度的關節型機器人,C-space通常為6維,因此無法在C-space中進行碰撞檢測,碰撞檢測只能在W-space中的節點處進行,雖然在C-space中RRT的步長為固定的Δθ,但是通過正向運動學將Δθ映射到W-space中所產生的位移Δp卻無法固定。
如圖3所示,在C-space中隨機樹以固定步長Δθ從節點1生長到節點2所引起的位移Δp大于障礙物W-obs的尺寸,而在W-space中節點1和節點2并沒有與障礙物發生碰撞,RRT算法會通過這次碰撞檢測,但在機器人從節點1向節點2運動的過程中卻發生了碰撞,由此可見,利用固定步長RRT方法對多自由度關節型機器人進行路徑規劃,無法確保生成一條避障路徑。
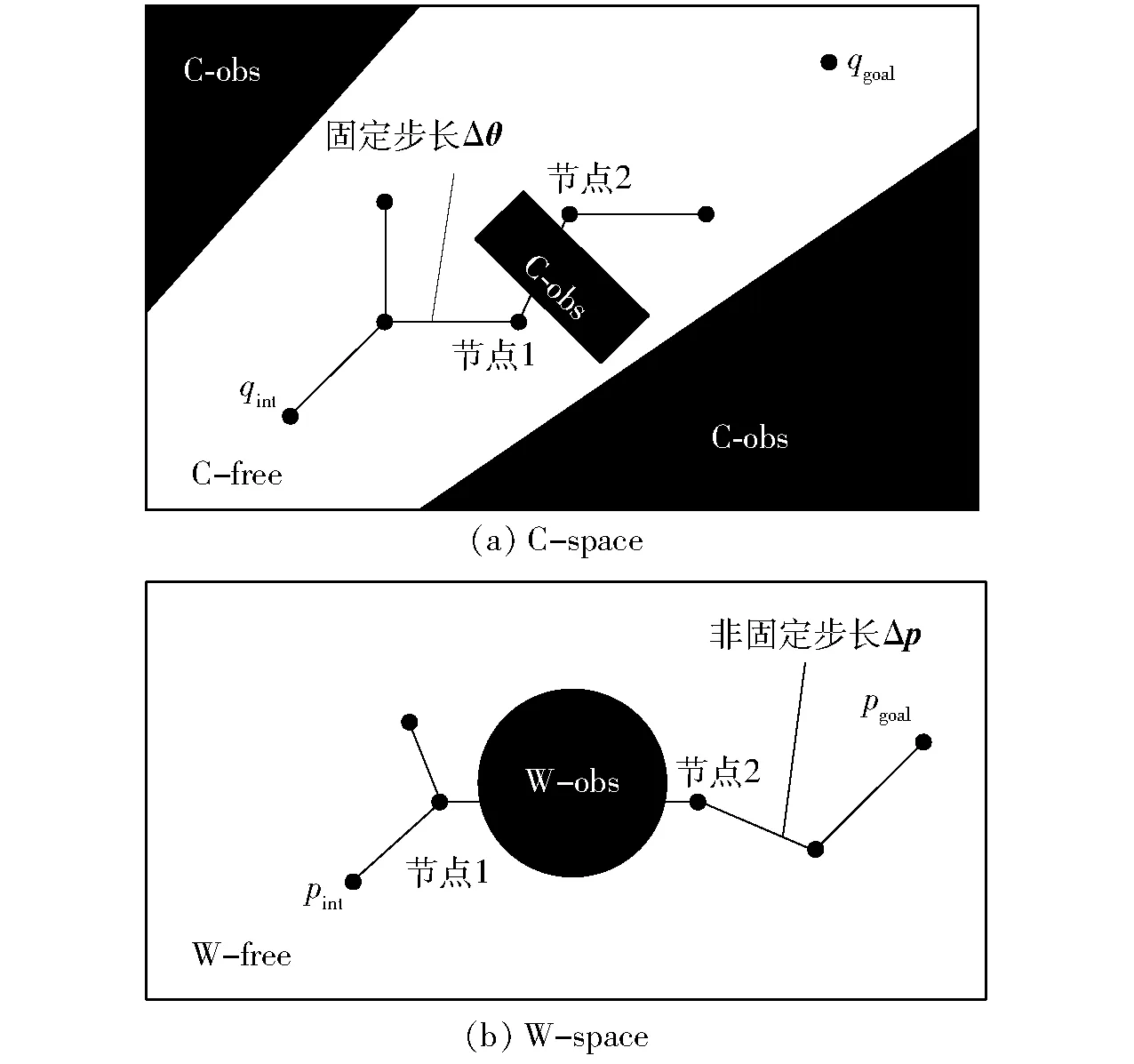
圖3 C-space和W-space中的步長關系Fig.3 Relationship of stepsize in C-space and W-space
3 自適應步長RRT
3.1 C-space和W-space的范數不等式構建
RRT方法以固定步長Δθ在C-space中進行隨機樹的生長無法控制在W-space中所產生的位移Δp,為了解決這一問題引入算子范數,構建C-space和W-space中步長的范數不等式,實現在C-space中控制W-space中Δp的目的。給定兩個向量范數‖·‖a∈Rm,‖·‖b∈Rn和矩陣A∈Rm×n,從屬于兩個向量范數的矩陣算子范數為
(8)
可得到范數不等式
‖Ax‖a≤‖A‖a,b·‖x‖b
(9)
機器人R1的C-space中步長Δθ∈R6,W-space中所對應的位移Δp∈R3,因此只需構造從屬于向量Δp和Δθ的矩陣算子范數,就可建立C-space和W-space的范數不等式,即構造一個矩陣A∈R3×6,滿足Δp=AΔθ即可通過不等式約束Δp的最大值,達到在C-space中控制步長的目的。矩陣A的構造過程如下:

(10)
其中
根據雅可比矩陣式(10)可改寫為
(11)
式(11)兩邊同乘以Δt可得
(12)
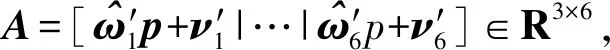
‖Δp‖w≤‖A‖w,c‖Δθ‖c
(13)
式中 ‖Δp‖w——W-space中的范數
‖Δθ‖c——C-space中的范數

3.2 C-space和W-space范數相容不等式改進
在式(13)中Δp特指雙機器人末端執行器的位移,當在C-space中給定一個步長Δθ機器人發生位移的最大位置不一定為末端執行器,也有可能發生在關節處,所以僅對機器人末端執行器的位移進行約束無法保證碰撞檢測的有效性,因此需改進范數不等式。
選用長方體包圍盒對雙機器人的連桿進行模型等效,設第i個連桿的頂點集合Li={pi1,pi2,…,pi8},i=1,2,…,6,則產生最大位移的位置必然在集合Li中,所以有
‖Δpmax‖w=max‖Δpij‖w(Δpij∈Li)
(14)
將式(14)代入式(13)可得
max‖Δpij‖w≤max‖Aij‖w,c‖Δθ‖c
(15)
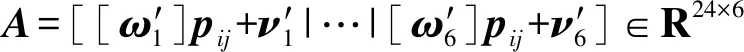
max‖Aij‖w,c∈R3×6
由此得到改進C-space和W-space范數不等式為
‖Δpij‖w≤max‖Aij‖w,c‖Δθ‖c
(16)
式中w、c的取值參考3.1節。
通過式(16)可以控制機器人任意位置由Δθ所引起的最大位移Δpij,完成雙機器人的全局性避障。
3.3 隨機樹被動生長
為了保持機器人之間的協調,在W-space中,隨機樹每一個節點的機器人末端執行器相對位置必須保持不變,因此兩個機器人在W-space中必須共享一顆隨機樹S_tree,但是在C-space中,機器人R1和R2的隨機樹卻是各自生長,故RRT算法無法控制雙機器人隨機樹的生長產生相同的S_tree。引入隨機樹被動生長方法,使機器人R2的隨機樹跟隨機器人R1隨機樹的生長,在機器人R2的隨機樹生長的同時,完成對S_tree的復制,如圖4所示,假設機器人R1的隨機樹為主動生長樹A_tree,機器人R2的隨機樹為被動生長樹P_tree,當A_tree在C-space中生長出一個新的節點A_node時,通過正向運動學將該節點映射到W-space中,完成共享隨機樹S_tree的生長并產生新的共享節點S_node,而P_tree新節點P_node的正向運動學須滿足
g1(A_node)=1S2g2(P_node)=S_node
(17)
因此機器人R2隨機樹P_tree只能根據式(17)進行生長,通過機器人R2的逆向運動學反解出P_node,為了避免機器人R2的關節位移產生跳動,估計解θ0應取在P_tree中A_node的父節點Anear_node所對應的節點Pnear_node。此時P_node為P_tree的新節點,若P_node通過碰撞檢測,則把P_node加入到機器人R2隨機樹P_tree中,完成一次雙機器人隨機樹的生長。
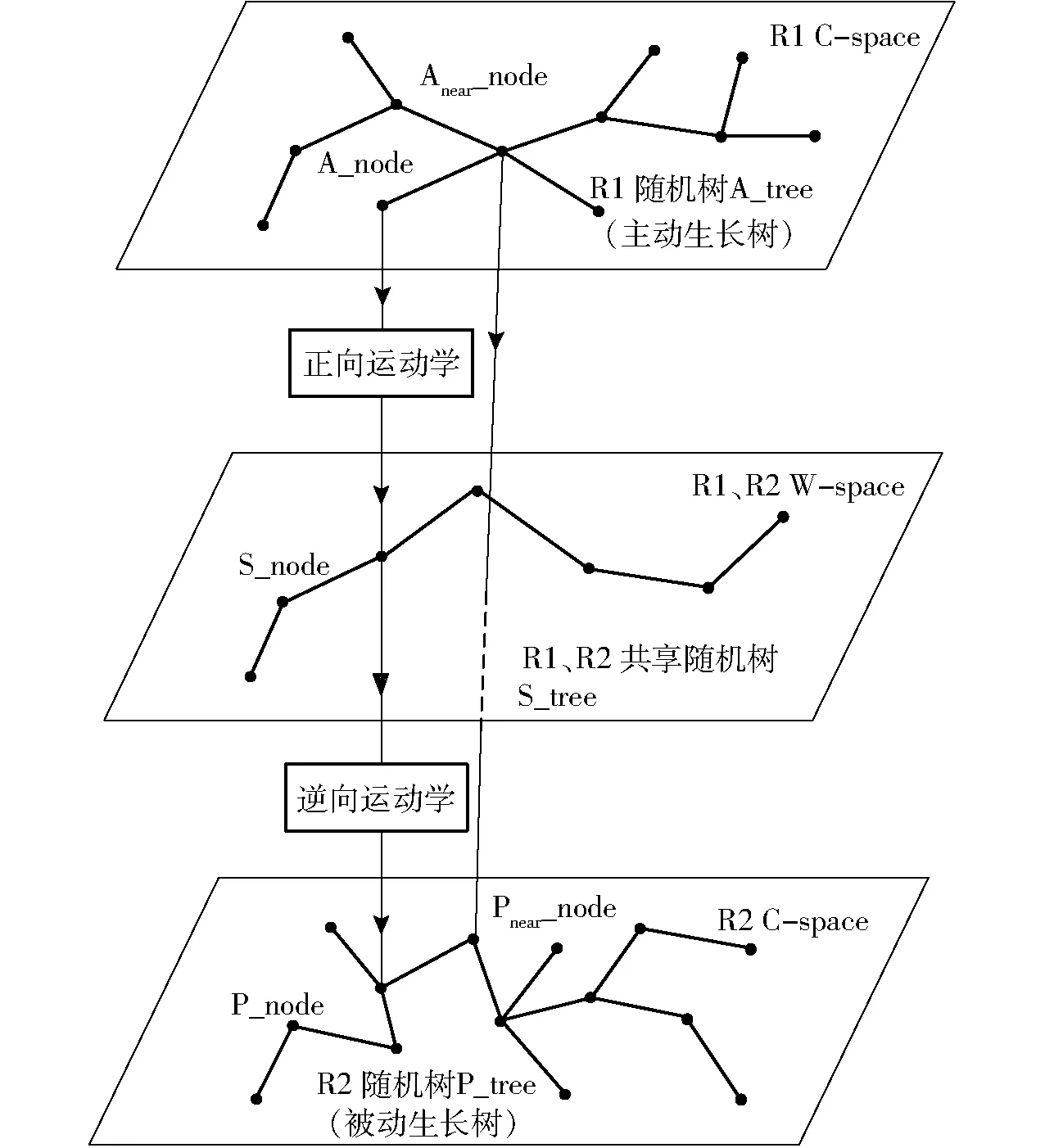
圖4 隨機樹被動生長Fig.4 Passive growing of random tree
3.4 雙機器人自適應步長RRT算法
基于3.2節所建立的范數不等式和3.3節提出的隨機樹被動生長方法,建立雙機器人自適應步長RRT算法,首先確定機器人在W-space中所允許的最大位移,令max‖Aij‖w,c‖Δθ‖c=Δpmax,代入式(16)可得
‖Δpijmax‖w≤max‖Aij‖w,c‖Δθ‖c=Δpmax
(18)
在構型空間中的步長為
(19)
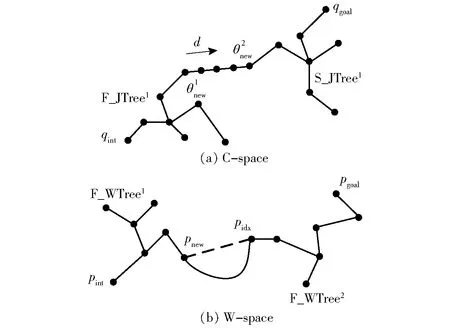
式中‖Δpmax‖w為算法的初始設定值,隨機樹每一次生長都會更新‖Aij‖w,c,從而使步長Δθ自動滿足式(19),此時Δθ的取值即控制了機器人工作空間步長Δpijmax又可以保證隨機樹的生長速率。為了提高算法的搜索效率,采用雙向搜索方法[21],雙機器人自適應步長RRT算法的偽代碼為
F_WTree=pint,S_WTree=pgoal
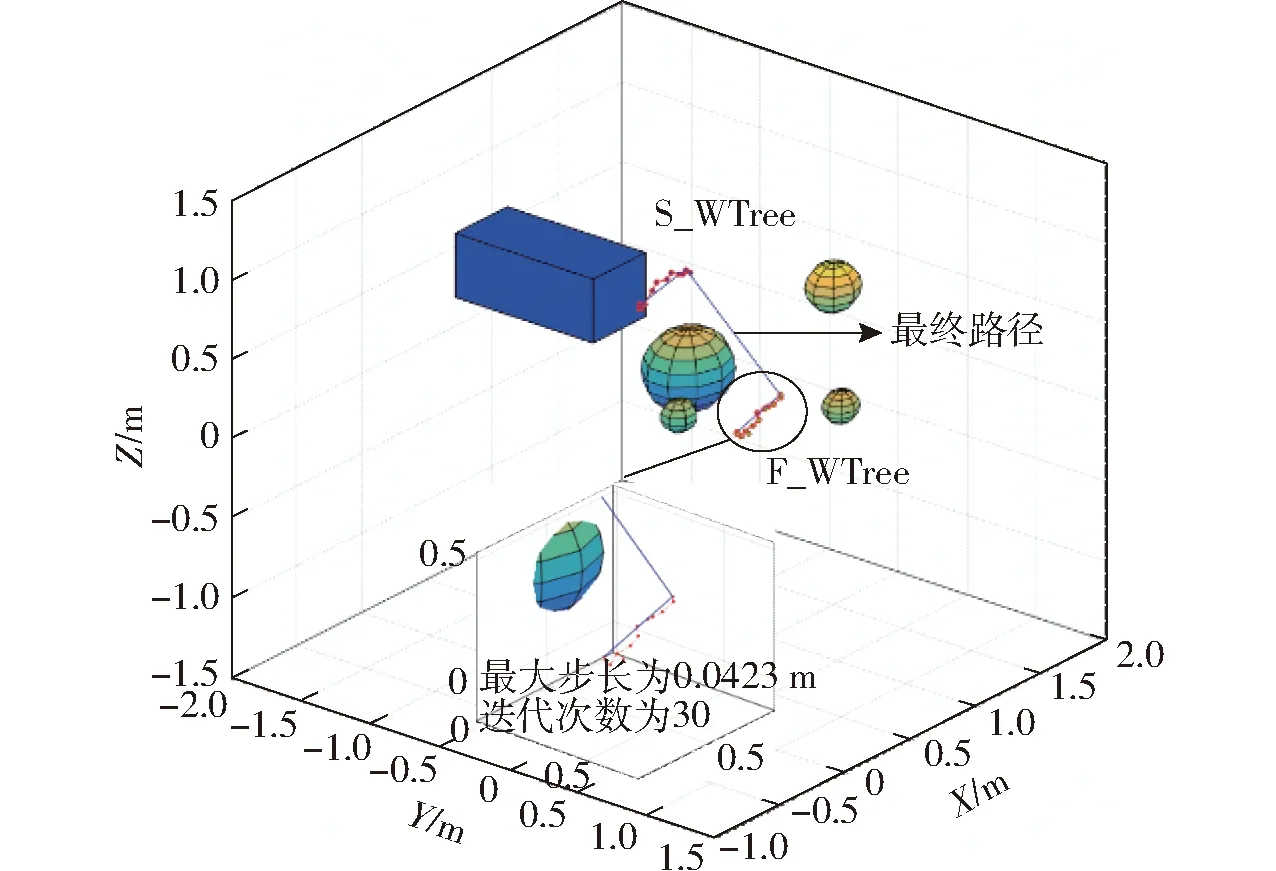
Whilen Tree_Add(pnew,F_WTree) return Path_J(S_JTree, F_JTree) return Path_W(S_WTree, F_WTree) else ExchangeTrees(S_JTree1, S_JTree2, F_JTree1,F_JTree2) end if end if end while Return Null 在C-space中分別定義以機器人R1、R2起始點和目標點為根的隨機樹F_JTree1、S_JTree1、F_JTree2、S_JTree2,在W-space中定義機器人R1、R2的共享樹F_WTree、S_WTree,在對隨機樹F_JTree1進行生長時,引入范數不等式,通過Stepsize( )計算并且約束步長Δθ,Stepsize( )的偽代碼為 算法實質上為式(19)的計算過程,其中涉及到w、c的取值,前文已有w=2,c=1,則Aij的算子范數定義如下 (20) Aij的算子范數求解偽代碼為 max=0 J=Jacc(θnew) fori= 1 to 6 forj= 1 to 8 fork= 1 toi temp=‖ωi×pij+νi‖2 if temp>max max=temp end if end for end for end for Return max 算法中的第2行是雅可比矩陣的求解,ωi和νi已經在前文中定義。 flag = true pidx= GetpointOnF_WTree1(idx, F_WTree1) d= GetDirection(pidx,pnew) dist= GetDistance(pidx,pnew) R= GetPose(pnew) while flag = true temp=pnew+s if CollisionFreeAndCheckJointLimits pnew=temp continue else break end if else flag = false end if end while 圖5 隨機樹的融合Fig.5 Merging of random tree 算法首先找出隨機樹S_WTree1中距離pnew1最近的點pidx,并確定隨機樹的融合方向d,算法的9~12行是以自適應步長的方式,在pnew和pidx之間插入n個節點,而后檢測這些節點能否通過關節限制檢測和碰撞檢測,若通過檢測則隨機樹F_WTree、S_WTree融合,機器人R1和R2在工作空間中走出以pnew1、pidx為端點的直線軌跡;若其中有節點發生碰撞或者超出關節限制,則隨機樹F_WTree、S_WTree無法融合,繼續進行隨機樹的生長。 當隨機樹F_WTree、S_WTree完成融合時,自適應步長RRT算法結束,得到雙機器人的協同運動路徑。 在Matlab中搭建雙機器人模型,如圖6所示,在雙機器人的W-space中分別設置4個球形障礙物,半徑分別為0.1、0.1、0.15、0.2 m,和一個長方體障礙物,尺寸為1.6 m×0.4 m×0.4 m,最小半徑為0.1 m,故設置Δpmax為0.1 m,即機器人R1和R2在W-space中的步長不能超過0.1 m,否則碰撞檢測將會失效,無法保證機器人有效避障,起點的坐標為(0.15,0.6,0),終點的坐標為(-0.55,0.6,0.6)。在模型中分別利用自適應步長RRT算法和RRT算法進行路徑搜索并進行對比。 圖6 雙機器人仿真環境Fig.6 Simulation environment of dual-robot 圖7為自適應步長RRT算法和步長為0.5 rad的RRT算法進行一次路徑搜索的結果,其中以起始點為根的隨機樹為F_WTree,以目標點為根的隨機樹為S_WTree,當兩棵樹達到融合條件時,隨機樹停止生長,經過圓滑處理產生一條距離最短的最終路徑。由于RRT算法的步長為0.5 rad,因此在工作空間中產生的步長也相對較大,所用的迭代次數較少,雖然RRT算法成功地生成了一條路徑,但從圖7a可發現,RRT算法在工作空間中所產生的步長具有明顯的跳動,在W-space中的步長最大值為0.155 7 m,大于Δpmax,無法保證碰撞檢測的有效性。自適應步長RRT所產生的步長具有很強的穩定性,且工作空間中最大步長為0.023 6 m,小于Δpmax,實現了雙機器人的避障路徑規劃。 進一步減小RRT算法的步長并與自適應步長RRT算法進行對比,其結果如圖8所示,圖8a為步長為0.3 rad的RRT的路徑搜索結果,相對于步長為0.5 rad的RRT,步長為0.3 rad的RRT在W-space中產生的步長平均值大幅減小,但仍然存在較大的步長跳動,步長最大值為0.112 9 m,大于Δpmax,仍然無法保證碰撞檢測的有效性,圖8b為自適應步長RRT算法第2次的路徑搜索結果,保持了在W-space中步長的穩定性,最大步長為0.032 7 m,小于Δpmax。 圖8 步長為0.3 rad的RRT與自適應步長RRT路徑規劃對比Fig.8 Comparison of path planning by RRT with stepsize of 0.3 rad and self-adaptive stepsize RRT 將RRT算法的步長縮小到0.1 rad并再次與自適應步長RRT算法進行對比,結果如圖9所示,在C-space中0.1 rad是一個非常小的步長,意味著機器人6個關節所產生的角度變化的總和為0.1 rad,因此隨機樹的每一次生長在W-space中所產生的步長會非常小,如圖9a所示,步長最大值為0.001 9 m,雖然遠小于Δpmax,但過小的步長使隨機樹的生長速度變慢,導致迭代次數劇增,是步長為0.3 rad的12倍。在相對嚴格的融合條件下,兩棵隨機樹難以融合,在可接受的時間內無法搜索出一條避障路徑。自適應步長RRT算法的第3次路徑搜索仍然保持了步長穩定的特性,且迭代次數約為步長0.1 rad RRT算法的1/2,同時兼顧了隨機樹生長速度和步長大小的控制。 圖9 步長為0.1 rad的RRT與自適應步長RRT路徑規劃對比Fig.9 Comparison of path planning by RRT with stepsize of 0.1 rad and self-adaptive stepsize RRT 通過對RRT算法步長的多次調整,確定0.2 rad為RRT算法在當前仿真環境下的步長匹配值,進行一次路徑搜索,其結果如圖10所示。 圖10 步長為0.2 rad的RRT路徑規劃Fig.10 Path planning by RRT with stepsize of 0.2 rad 算法的最大步長為0.042 3 m,迭代次數為30次,基本與自適應步長RRT算法相近,步長仍有輕微跳動,最大步長已經控制在Δpmax的范圍內,可以滿足碰撞檢測的要求。使用RRT算法進行路徑搜索時,從上述的仿真過程可以發現,找到合適的步長通常需要多次調試才能夠確定,而自適應步長RRT只需要指定Δpmax,就可自動調整C-space中的步長來控制W-space中產生步長,當機器人的工作環境發生變化時,只需根據環境模型指定新的Δpmax就可再次進行路徑搜索,而固定步長RRT算法需再次對步長進行多次的調試。另外,傳統的RRT算法存在步長過大所導致的碰撞檢測失效問題,而自適應步長RRT算法,通過式(16)把機器人的關節、連桿和末端執行器的位移全部約束在Δpmax內,可得到機器人全局性的無碰撞路徑。 分別對自適應步長RRT和步長0.5、0.3、0.1、0.2 rad的RRT進行50次仿真,其結果如表1所示。表中pmax為W-space中步長的最大值,當pmax大于Δpmax時,算法失效。從表1可以看出,RRT算法隨著步長的減小,pmax的最大值和平均值也隨之減小,但迭代次數會不斷增加。當步長為0.5 rad時,RRT算法的步長較大,失效次數為37次,失效概率為74%,當進一步減小步長至0.3 rad時,雖然pmax的平均值降到可接受的范圍內,但仍有14次失效,失效概率為28%。當步長為0.1 rad時,失效次數雖然為0,但過小的步長導致迭代次數的劇增,而自適應步長RRT既保證了算法的失效概率為0,同時又控制了算法的迭代次數。當取RRT的步長為0.2 rad時,可得到與自適應步長RRT相接近的最大步長與迭代次數。 表1 不同步長RRT與自適應步長RRT步長、迭代次數和失效次數Tab.1 Maximum stepsize, iterations and invalid times of RRT and self-adaptive stepsize RRT 針對RRT算法無法控制雙機器人在W-space中步長的問題,提出了自適應步長RRT算法。通過構建C-space和W-space的范數不等式,把隨機樹每一次生長所產生的機器人位移約束在給定范圍內,在利用自適應步長RRT進行路徑規劃時,只需根據機器人的工作環境指定Δpmax,省去了RRT算法為確定步長而進行多次調試的耗時過程;提出了隨機樹被動生長方法,實現了雙機器人末端執行器同位置不同構型的路徑規劃,結合自適應步長RRT算法完成了雙機器人的協同路徑規劃。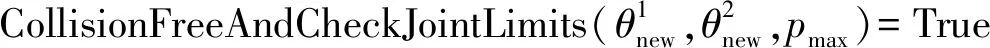
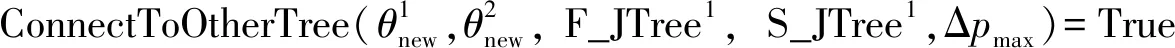
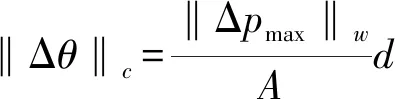
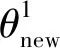
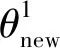

4 仿真
4.1 單次仿真
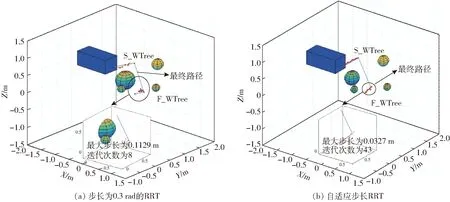
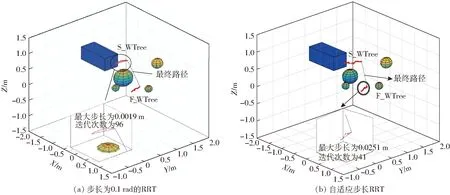
4.2 多次仿真

5 結束語

