追溯“缺失”讓學生的思維自然地流淌

鄭 良

(安徽省靈璧第一中學 234200)

一、問題提出

學生A到辦公室向教師B請教以下兩個問題：

問題1 在△ABC中，內角A、B、C所對的邊分別為a、b、c，且滿足a4+b4+c4=2(a2+b2)c2，則角C=____.

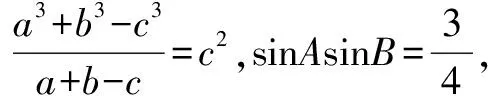
教師B看了一下題目，很快地給出以下解答，然后讓學生回去理解體會.

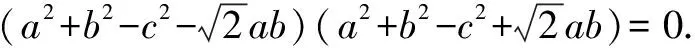
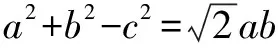
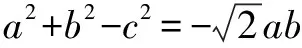
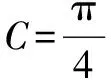
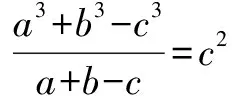
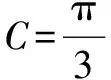
綜上所述，△ABC為等邊三角形.

教師B解題能力很強，給出的也是通性通法，問題看似解決.令筆者深思的是，學生為什么不會做？通過教師的解答，學生能領悟多少？下次遇到類似問題能夠解決嗎？學生的思維能力是否得到真正的提高？

二、問題分析

問題1中如何確定C？正弦定理和余弦定理可以解決確定三角形的所有問題，但正弦函數在(0,π)上先增后減，還需結合其它條件認定角的范圍(值)，而余弦函數在(0,π)上單調遞減，逆用函數單調性即可確定角的范圍(值).條件是三角形各邊的關系，若直接采用正弦定理，將會出現各內角正弦的四次方，嘗試兩次降冪構建關于某個內角的三角方程，式子繁雜；若采用余弦定理，只需將四次式按目標(余弦定理的結構)進行配湊，考慮到等式右邊為a2+b2與c2的乘積，移項因式分解即可.

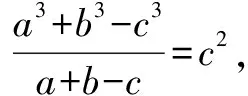
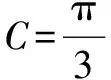
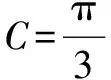
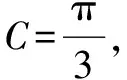
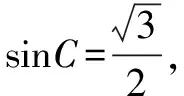
三、案例鏈接

教師B的處理不是個案，下面給出最近隨堂聽課的教學案例(這里不再以對話形式給出，解(證)法1為任課教師給出的問題解答)，并結合自己的分析思考.

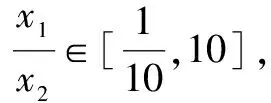
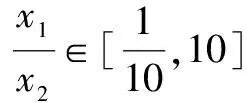
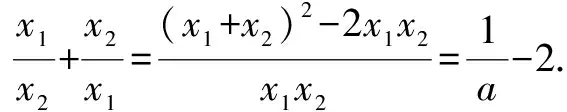
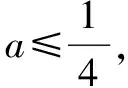
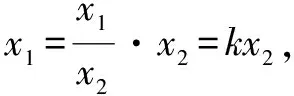
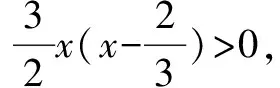
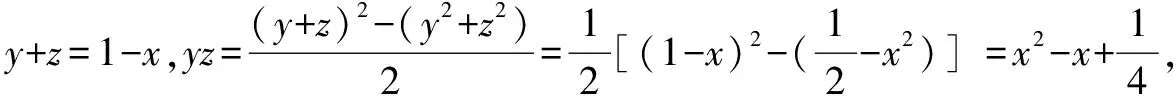
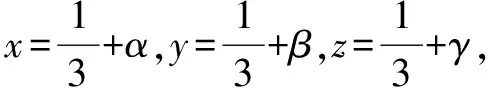
評析任課教師照本宣科，認為題目條件比較復雜，而結論比較簡單，不太容易入手，可用反證法證明；證法2利用不等式的性質構建關于x的不等式；證法3逆用根與系數的關系構建關于t的方程；證法4根據平均值增量換元，利用平方的非負性.

四、教學感悟

教學需要“接受”，但接受不等同于直接“告知”結論.令人遺憾的是，“一個結論，幾項注意”“一背二套”“例題講解加習題演練”仍然是教學的主旋律.筆者給出的解法為課堂慢等花開的部分成果，貼近大多數學生的“最近發展區”，更符合他們的認知水平.追溯教學過程中的“缺失”，及時彌補方能亡羊補牢.

1.學生主體性的“缺失”

教育就是生長，其本質是人的發展，也就是說，教育的過程就是發覺人的天性、潛能以及潛在價值的過程.課堂，是學生的課堂.案例中的教學沒有顧及學生的“心理”感受和需要，強行學生消費.文獻[1]中，張奠宙教授在談到中國傳統的數學教育時，主張教師主導下發揮學生主體作用時說：“‘傳道、授業、解惑’并不單指教師的作用，而主要是教師的責任，至于怎么做，不能只以教師的主觀武斷來實行教學，要以學生為主體進行安排，教師是教學的組織者、指導者、合作者，同時也是領導者和示范者.” 同時指出“教師的示范，非常重要，現在幾乎忽略不提，很遺憾.”示范不是澆灌.教師應當在題意的理解、方法的選擇、技巧的提醒、書寫的規范等主要環節做足示范.對于學生不會的問題，教師要讓學生說出其理解、困惑，在學生“最近發展區”上引領示范，讓學生在體驗中學習.

2.解題方法的“缺失”

案例反映學生對解題方法、變換技能掌握不到位，無法根據題意選擇合理的解題路徑.解題需要見微知著，能根據條件引發對問題的整體思考.這需要教學中學生對概念、結論的準確認知，對過程切身經歷，但“掐頭去尾燒中間”的教學方式導致學生的學支離破碎，思維千瘡百孔，遇到類似問題想不起、做不到，張冠李戴不足為奇.課堂必須是開放的：學生要有自主學習、自主思考的時間，學生要有合作的機會、交流的平臺，學生要帶著問題去探究，并且要讓學生嘗到這一系列活動的成果.讓學生知曉概念的發生發展過程、結論背景及推導方法、體會思想方法的邏輯關系，使其知其然知其所以然.解題時才能從直覺表象走向自覺分析并不斷反思優化.章建躍博士認為：“課堂教學中，如果我們的教學不能打動學生，學生對我們的講解無動于衷，那么他們就不可能有心領神會的心靈共鳴，我們講得再精彩也只能是無功而返.”解題過程不能把學生想象過高(低)，要關注學生的多維感受，順應學生的思維，量力而行.

追溯“缺失”，崇尚自然.“要以數學地認識問題和解決問題為核心任務，以數學知識的發生發展過程和理解數學知識的心理過程為基本線索，為學生構建前后一致邏輯連貫的學習過程，使他們在掌握數學知識的過程中學會思考.”