判別常數項級數斂散性易犯錯誤分析研究

景慧麗

(火箭軍工程大學 基礎部，陜西 西安 710025)

引言

無窮級數是高等數學的一個重要組成部分，它是表示函數、研究函數性質以及進行數值計算的一種工具[1]251.總體來說，無窮級數包括兩部分內容：常數項級數和函數項級數，而函數項級數的很多性質和結論都是借助于常數項級數得到的，所以，常數項級數斂散性的判別尤其重要.在高等數學課程中判斷常數項級數斂散性的方法有很多，如利用級數收斂與發散的概念、利用收斂級數的性質、利用比值審斂法、利用萊布尼茨定理[1]265等等.每種方法也都有自己的使用條件和使用范圍,例如，比值審斂法只適用于正項級數，而萊布尼茨定理只適用于交錯級數.但是，筆者在教學中發現，學員在判斷常數項級數的斂散性時經常出錯，他們不考慮判別法則成立的條件，誤用、亂用情況經常發生.為了幫助學員掌握并能熟練應用常數項級數斂散性判別方法，筆者把學員在解題時經常出現的錯誤進行了分析總結，歸納了常見的錯誤類型，并且就每種錯誤給出了例題、錯解分析及正確解法.

1 利用級數收斂的必要條件來判斷級數收斂

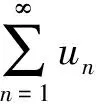
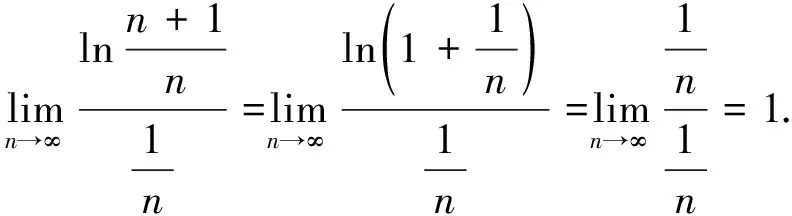
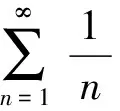
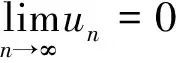
2 顛倒級數收斂與級數的和的邏輯順序

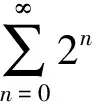
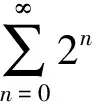
[正確解法] 本題有兩種解法.

解法一：利用等比級數的結論，即由于該級數是公比q=2的等比級數，由于|q|=2>1，因此該級數發散.

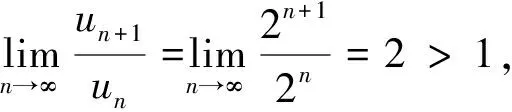
3 用錯誤的性質來判斷級數的斂散性

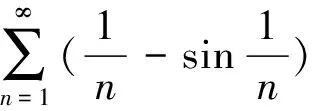
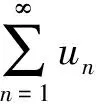
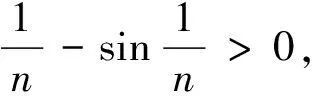
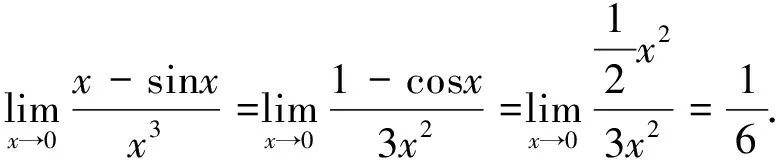
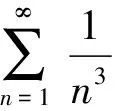
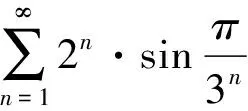
4 亂用比較審斂法(或比較審斂法的極限形式)

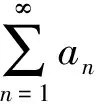
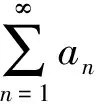
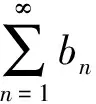
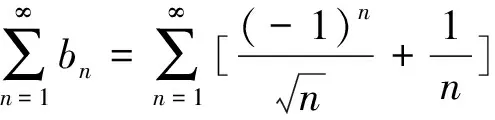
5 誤把比值審斂法理解為充要條件

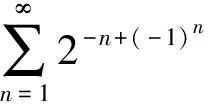
[錯解] 令un=2-n+(-1)n，則

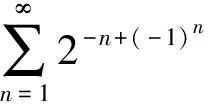
[正確解法] 本題應用正項級數的根值審斂法進行判定

令un=2-n+(-1)n，則

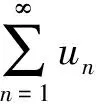
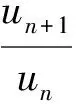
[正確解法] 本題應用正項級數的比較審斂法進行判定.

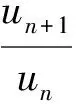
又u3即u3

下面用歸納法證明對任意的n，有un+1成立.

假設un則un+1即un+1成立.

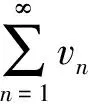
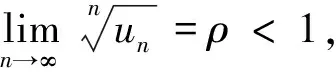
注5 比較審斂法、比較審斂法的極限形式、比值審斂法及根植審斂法都只適應于正項級數，而且這些判別法都是充分不必要的.萊布尼茨定理只適應于交錯級數，而且也是充分不必要的，當定理的條件成立時，只能得到級數收斂的結論，當不滿足定理的條件時，是不能得到級數發散的結論的.

6 結語

以上就是學員在判別常數項級數斂散性時易犯的錯誤，其實只要學員理解了級數的概念、性質，掌握了判別級數斂散性方法成立的條件及使用范圍，上述錯誤都是可以避免的.另外，教員要正確看待這些“錯題”資源，這些都是非常寶貴的教學資源，正如心理學家蓋耶所說：“誰不考慮嘗試錯誤，不允許學生犯錯誤，就將錯過最富成效的學習時刻.”[3]在教學中，教員要主動挖掘學員“錯題”中的“閃光點”，及時進行探究、分析和講評，既可以為學員創造新的學習機會，提高教學質量，還可以培養學員的問題意識，培養學員發現問題、解決問題的能力[4].