全下肢直接數字X線攝影推算四川漢族女性身高

崔井會，駱瑩貞，常云峰，彭釗，鄧莉萍，張奎，鄧振華

（1.四川大學華西基礎醫學與法醫學院，四川 成都 610041；2.中南大學基礎醫學院法醫系，湖南 長沙410013；3.四川大學華西醫院，四川 成都 610041）

個體身高的推算是法醫學研究與實踐中一項重要的基礎性工作，特別是在如爆炸、碎尸、高度腐敗及白骨化等不能進行DNA身源鑒定的案件中。近年來，隨著人口流動的增加，我國無名尸體案件亦隨之增加，對骨骼個體識別的需求日益迫切。為了滿足案件偵查的需要，國內學者[1]開始引用國外的有關研究成果，對中國人骨骼個體識別的方法進行了廣泛深入的研究。隨著經濟的發展，國人體質有了整體提高，同時受地域、種族、性別、年齡和個體差異的影響，身高推算的研究已成為常規性研究。而我國身高推算相關研究中的研究樣本多來源于20世紀80年代，用于當代國人身高推算準確性較低。因此，建立適合當代國人身高的推算模型就顯得格外重要。

1899年，PEARSON[2]首次將長骨長度與身高進行回歸分析，得出了利用股骨推斷身高的數學模型，成為法醫學中推斷身高的經典方法。此后，有許多國內外學者[3-7]利用四肢長骨及長骨碎片針對不同的種族與人群建立了相應的身高推算數學回歸模型。研究結果均顯示，四肢長骨與身高的相關性較高，并以利用股骨進行身高推算最為準確。我國利用四肢長骨進行身高推斷的研究大多采用尸體或干骨，樣本量偏少，特別是對女性身高推斷的研究，而且利用影像學方法進行身高推斷大部分針對的是未成年人[4-5，8-9]。因此，本研究旨在采用直接數字X線攝影（direct digital radiography，DDR）技術，測量四川地區漢族女性全下肢相關指標，構建當代國人身高推算的數學回歸模型，為法醫學實踐積累基礎數據。

1 材料與方法

1.1 研究對象

本研究的所有樣本均來自四川大學華西醫院，共收集四川地區漢族健康女性全下肢DDR圖像樣本171例。

納入標準：（1）籍貫為四川；（2）健康女性；（3）漢族；（4）所拍攝DDR圖像質量清晰，可清楚觀察到測量標志點。

排除標準：（1）下肢有骨折、畸形或手術史者；（2）曾經服用或正在服用影響骨代謝與生長發育的藥物者；（3）患有影響骨生長、發育與代謝的全身性疾病者。

本研究符合醫學倫理學相關規定。

1.2 方法

1.2.1 身高測量

在攝片前，按照《體質測定》中身高測量方法[10]、用SZG型身高坐高計（南通悅健體測器材有限公司）測量每個個體的身高（y，cm），精確至0.1cm。

1.2.2 DDR圖像采集

采用大平板多功能數字化透視/攝影系統［Sonial Vision SafireⅡ，島津企業管理（中國）有限公司］拍攝，條件為：管電壓70～95kV，管電流250～400mA，曝光時間5.0～8.0 ms，固定球管中心至成像板的距離為120cm。拍攝體位：仰臥負重站立位（檢查者光腳仰臥于檢查床上，雙足分立于腳踏板上，足尖向前，雙下肢伸直，髕骨位于膝關節正前方，檢查床與水平面成40°～45°夾角，X射線球管與檢查床垂直）。采用系統自帶的Syngo-Imaging VB36C圖像后處理軟件進行圖像后處理及測量，精確至0.1cm。

1.2.3 觀測指標

本研究參照傳統法醫人類學骨骼測量方法，結合全下肢DDR影像特點選取左下肢以下骨性標志點及測量指標（圖1）。

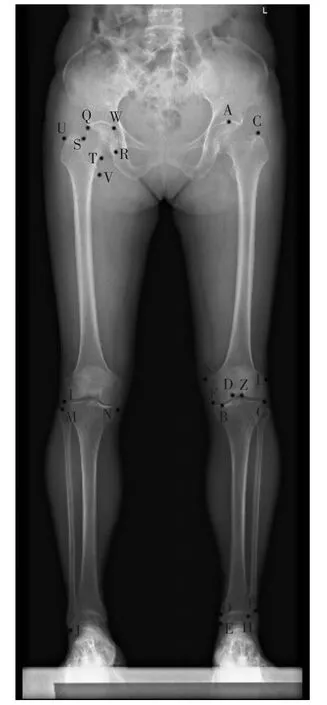
圖1 DDR圖像上的測量標志點

股骨最大長（x1）：股骨頭最高點（A）至內外側髁最低點（B）之間的垂直距離；

股骨生理長（x2）：股骨大轉子最上點（C）至內外側髁最低點（B）之間的垂直距離；

脛骨最大長（x3）：脛骨髁間棘最高點（D）至內踝最低點（E）之間的垂直距離；

脛骨內側最大長（x4）：脛骨內側平臺最內上緣點（F）至內踝最低點（E）之間的垂直距離；

脛骨外側最大長（x5）：脛骨外側平臺最外上點（G）至脛骨外側最下點（H）之間的垂直距離；

腓骨最大長（x6）：腓骨頭最上點（I）至外踝最下點（J）之間的垂直距離；

髁間寬（x7）：股骨內外側髁最外側點（K與L）之間的水平距離；

脛骨平臺最大寬（x8）：脛骨平臺兩側最外側點（M與N）之間水平距離；

脛骨遠端最大寬（x9）：脛骨遠端兩側最外側點（O與P）之間的水平距離；

股骨頭最大寬（x10）：股骨頭最外上點（Q）與股骨頭最內下點（R）之間距離；

股骨頸最小寬（x11）：股骨頸最狹窄處寬度（S與T之間距離）；

股骨大小轉子間最大寬（x12）：大轉子最外側點（U）與小轉子最內側點（V）之間距離；

股骨頭最大長（x13）：股骨頭最內上點（W）到線段UV的垂直距離；

內側髁間棘（Z）至內側平臺最內上點之間水平距離（x14）：D與F之間距離；

外側髁間棘至外側平臺最外上點之間的水平距離（x15）：Z與G之間距離。

對由于體位等原因造成左下肢測量標志點遮擋或者不清晰的圖像測量右下肢。171例樣本中，139例測量單側下肢，32例測量雙下肢。

1.2.4 統計方法

應用SPSS 21.0統計學軟件，首先對總體樣本的身高、年齡及各測量指標進行描述性統計分析，對身高及各測量指標進行單樣本Kolmogorov-Smirnov檢驗，分析其是否符合正態分布。采用配對樣本t檢驗分析32例雙側下肢測量值之間的差異性。從樣本中隨機選取15例，由同一測量者對測量指標進行2次測量（2次測量時間間隔大于1月），采用獨立樣本t檢驗進行一致性檢驗。以各指標為橫坐標，身高為縱坐標繪制散點圖，觀察測量指標與身高之間是否存在線性關系。分析各測量指標與身高的相關性（r），利用相關性較高的測量指標建立身高推算的一元線性回歸方程。考慮到不全長骨或骨骼測量標志點缺失的情況，納入多個測量指標采用逐步回歸分析的方法建立多個多元線性回歸方程。身高推算的逐步回歸方程，就是將測量指標逐個引入回歸模型，每引入一個新的測量指標都對已入選回歸模型的指標逐個進行檢驗，將經檢驗認為不顯著的指標刪除，以確保每次引入新指標之前回歸方程中只包含顯著性指標，經過反復的入選與刪除，直到既沒有顯著的指標選入方程，也沒有不顯著的指標從方程中剔除為止，以保證最后所得到的測量指標的集合是最優的。檢驗水準α=0.05。

1.2.5 回代檢驗

按照納入標準重新收集29例樣本，回代檢驗上述回歸方程的準確性。

2 結 果

描述性統計分析顯示，樣本年齡11.0～79.0歲，平均年齡47.6歲，平均身高（153.5±6.7）cm。各測量指標與身高的描述性分析結果見表1。

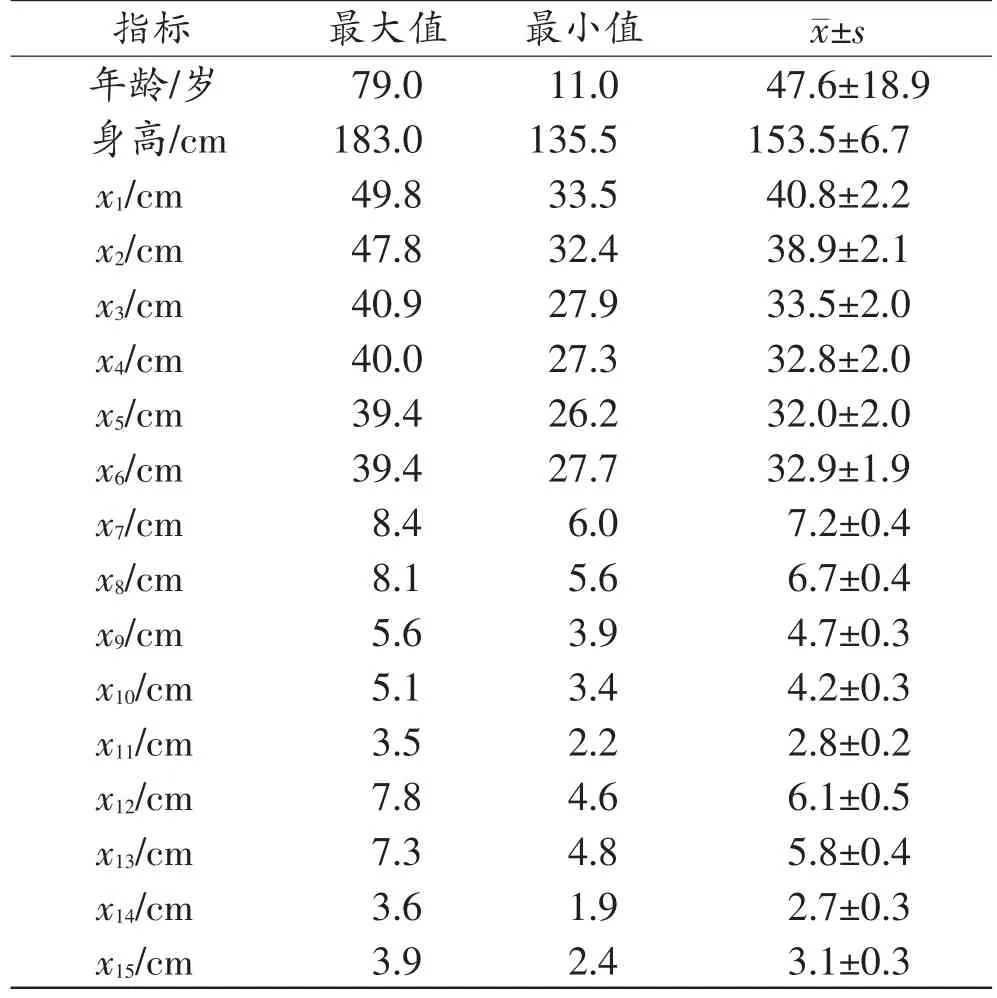
表1 年齡、身高及各測量指標的描述性分析（n=171）

配對t檢驗顯示，雙側下肢的測量值之間差異無統計學意義（P＞0.05）。一致性檢驗顯示，同一測量者兩次的測量結果之間差異無統計學意義（P＞0.05），具有一致性。

所有測量指標（x1～x15）及身高均符合正態分布。x1與身高的相關性最高（r=0.856）；x2～x6與身高具有較高的相關性，r由高到低依次為：x6（0.836）＞x5（0.829）＞x3（0.828）＞x2（0.825）＞x4（0.821）；x10、x12、x13與身高的相關性偏低，r分別為0.459、0.494、0.525；其余的測量指標（x7～x9，x11、x14、x15）與身高的相關性較差，r在 0.044（x14）～0.348（x11）。

利用相關性較高的測量指標建立一元線性回歸方程6個（表2），所有方程均有統計學意義（P＜0.05），復相關系數（R）為0.821～0.856，標準估計誤差（standard error of estimate，SEE）為3.453～3.812cm。利用所有測量指標，采用逐步回歸分析方法建立身高推算多元線性回歸方程4個（表3），所有方程均有統計學意義（P＜0.05），R為0.874～0.897，SEE為2.994～3.258 cm。單獨應用股骨或脛骨的測量指標采用逐步回歸分析方法建立身高推算的多元線性回歸方程3個（表4），所有方程均有統計學意義（P＜0.05），R為0.837～0.875，SEE為3.254～3.662cm。

運用以上身高推算數學模型，對29例回代檢驗樣本的身高進行推算，結果顯示，所有身高推算方程的平均絕對誤差為（2.485～3.432）cm，±1SEE準確率在35.7%～60.7%，±2SEE準確率為75.0%～92.9%。回代檢驗準確率最高的檢驗結果見表5。

表2 利用單個測量指標（x1～x6）建立的身高推算一元線性回歸方程

表3 利用所有測量指標采用逐步回歸分析方法建立的身高推算多元線性回歸方程

表4 利用股骨或脛骨測量指標采用逐步回歸分析方法建立的身高推算多元線性回歸方程

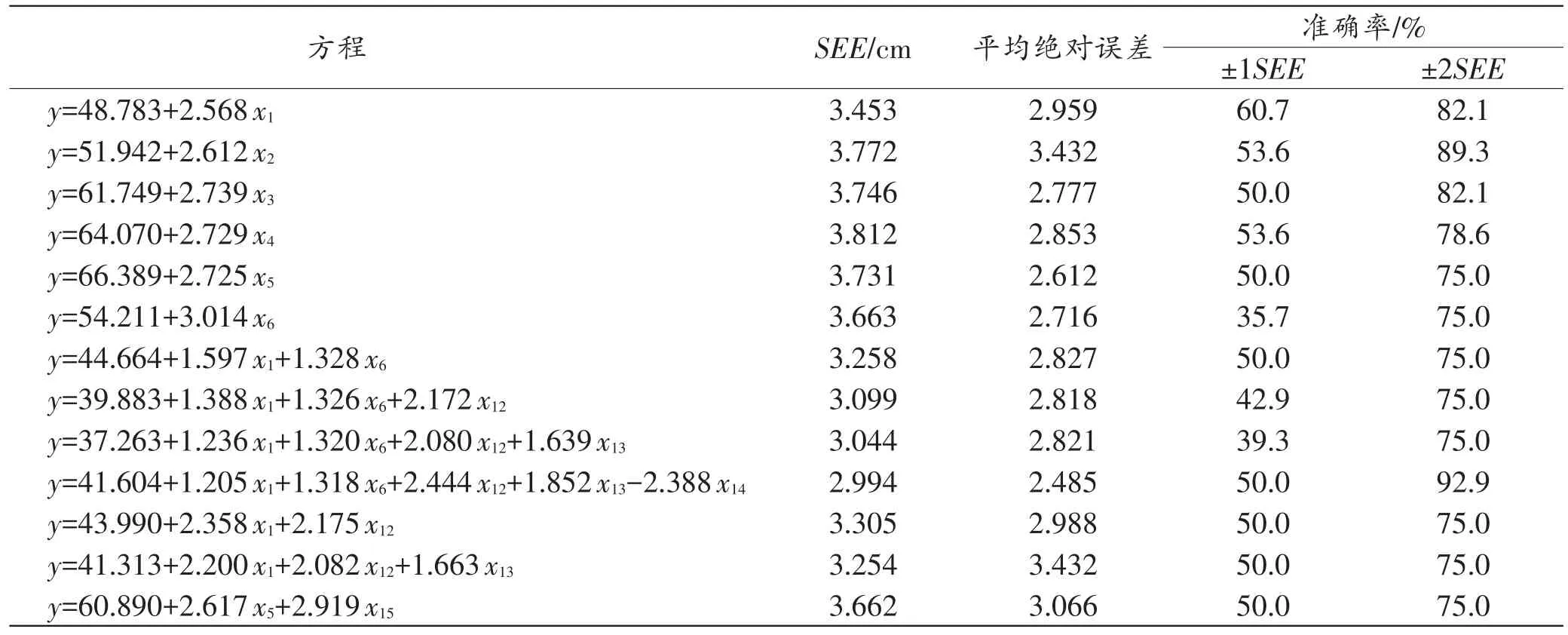
表5 方程準確率回代檢驗結果

3 討 論

身高推算作為法醫學個體識別中的重要組成內容，一直是國內外學者研究和關注的重點之一。早在1899年就已有利用股骨進行身高推算的研究[2]，建立了利用股骨進行身高推算的回歸方程，并成為身高推算的經典方法。為了更加適應實際檢案的需要，自20世紀60年代開始，陸續有學者對殘存長骨進行測量研究，以期找到利用部分長骨或長骨碎片進行身高推算的方法：2002年，張繼宗[8]建立了中國女性不完整長骨推斷身高的回歸方程；2007年，CHIBBA等[3]應用脛骨近端及遠端測量指標構建了不完全脛骨的身高推算方程；2001年，李鐵英等[11]建立了基于股骨、脛骨、尺骨、肱骨骨性標志測量值的多元回歸方程，同時考慮到長骨近端、遠端或兩端同時缺失的情況。以上研究的樣本都來自尸體或者干骨，由于受到樣本來源的限制，大多數研究樣本量較小。也有學者探索利用體表解剖標志進行身高推算的方法：2003年，OZASLAN等[9]通過測量轉子高度、大小腿長度、足長等活體體表指標建立了身高推算模型；2013年，NOR等[12]也做了相似的研究，并得出了相似的結論。利用體表標志點進行身高推算方法簡單易行，在一定程度上突破了樣本量的限制，建立的身高推算模型也更加適合當代人群，但不能忽略受軟組織等影響造成測量誤差的存在。隨著醫學影像技術的發現與發展，其在骨骼成像及測量方面的優勢迅速顯現并很快應用于法醫人類學的研究。X線攝影技術是一種非破壞性的檢查方法，重復性好，X線片易存儲，在法醫人類學中主要通過對活體、尸體或含有骨骼的肢體的影像學資料進行年齡、性別以及身高的推斷。1962年，TELKKA等[13]應用長骨X線片對兒童進行了身高推算。2007年，周曉蓉等[4]應用X線攝影技術對上肢長骨與身高的關系進行了研究。2017年，BRITS等[14]應用磁共振技術對青少年股骨與身高的關系進行了研究。利用放射學方法進行身高推算的研究是以活體為研究對象，樣本來源范圍廣，樣本量不受限制，能夠清晰顯示測量標志點，使測量結果更加準確。

我國應用數字化X線攝影技術進行身高推算的研究少，受X線攝影機曝光范圍所限，研究主要局限于青少年，并且主要研究脛腓骨或股骨。鄭濤等[5]應用357例14～18周歲青少年的肱骨、尺橈骨及脛腓骨計算機X線攝影（computed radiography，CR）片（其中肱骨及尺橈骨94例，脛腓骨163例）建立了身高推算回歸方程，結果顯示，女性組回歸方程的R為0.710～0.895，SEE為（3.075～4.084）cm。范濤等[15]測量了422例（男207例，女215例）CR片的脛腓骨長度指標，建立了不同性別、不同年齡段身高推算的一元線性回歸方程35個，其中女性組回歸方程的R為0.827～0.850，SEE為（2.68～2.86）cm。以上研究均以CR片為研究對象，存在橫向和縱向上的放大問題，雖然都經過校正，但操作方法相對復雜。本研采用的是全下肢正位DDR圖像，不存在放大率問題，不需要校正，操作相對較簡單。本研究所有測量指標中，股骨、脛骨、腓骨長度相關指標與身高具有較高的相關性，并以股骨最大長度與身高的相關性最好，這與既往的研究結果[5-7，11-14]一致。利用全下肢相關指標建立一元線性回歸方程6個，多元線性回歸方程7個，所有方程的R在0.821～0.897，SEE在 2.994～3.812 cm。與鄭濤等[5]的研究結果相比，本研究所用的樣本量較大，且所得線性回歸方程的R及SEE均較高；與范濤等[16]的研究結果相比，R較高，但SEE較大，這可能與本研究樣本中包含未成年人而范濤等的研究樣本均為成年人有關，同時地域差異的影響也不能排除。經檢驗，所有方程的平均絕對誤差為（2.485～3.432）cm，±1SEE準確率為35.7%～60.7%，±2SEE準確率為75.0%～92.9%，方程準確性較高，并以方程y=41.604+1.205x1+1.318x6+2.444x12+1.852x13-2.388x14的平均絕對誤差最小（2.485 cm），±2SEE準確率最高（92.9%）；方程y=48.783+2.568x1的±1SEE準確率最高（60.7%）。回代檢驗表明，多元回歸方程準確性優于一元回歸方程，多指標推算優于單指標。

本研究采用大平板多功能數字化透視/攝影系統采集全下肢正位圖像，拍攝體位與身高測量體位相似，保證了拍攝圖像時身高與站立時身高的一致。該設備拍攝的圖像具有一次性采集、圖像清晰、分辨率高、圖像銳利、解剖標志點清晰等特點，同時還具有強大的圖像后處理功能，能直接在其工作站上進行窗寬、窗位的調整，測量角度、距離等，同時具有便于存儲、傳輸等特點，非常適用于臨床研究及檢案鑒定工作。同時，該成像系統采用了狹縫式同步掃描技術原理，很好地解決了縱向放大率的問題，使測量值與真實值一致，并且其掃描范圍廣，能一次性完整地呈現全脊柱、全下肢等圖像，特別適合于法醫人類學研究工作，且可應用于碎尸案或無名尸體解剖檢驗前的影像檢查，在法醫人類學研究方面具有廣闊的應用前景。

本研究利用影像學技術，以活體為研究對象進行身高推算，所建立的回歸方程平均絕對誤差較小，同時考慮到下肢單塊骨、多塊骨及骨骼碎片的情況，具有較強的實用性。但由于未成年人進行全下肢攝影檢查者較少，使樣本收集較困難，本次并未做針對性研究，同時本次的研究樣本具有一定的地域、民族、性別的特異性，其他地區或民族的身高推算應用該方程具有一定的局限性，需做進一步研究。