基于張量網絡算法的自旋梯子系統的弦序參量的研究

李生好, 雷國平

(1.重慶工程職業技術學院, 重慶 402260; 2.重慶大學現代物理中心, 重慶 400060; 3.重慶三峽學院電子與信息工程學院, 重慶 404000)

1 引 言

近年來, 量子信息理論為量子多體系統的量子相變的研究掀開了嶄新的一頁. 通過量子多體系統的基態波函數得到的局域序參量或非局域序參量來研究量子相變, 這主要由于兩方面的進展, 一是不斷發展的基于張量網絡表示的準嚴格數值算法, 為量子多體系統的基態波函數研究提供了更加有效的工具; 二是量子多體系統不管是否存在朗道對稱性破缺序還是存在其他非局域序, 為了更好地理解所涉及的內稟序, 系統基態波函數均可以用來刻畫重整化群流和相應的量子相變[1-4].

在凝聚態物理研究中, 自旋梯子系統已經成為一個課題, 并取得了很大的進展[4-8]. 人們通過對自旋1/2的海森堡多腿自旋梯子類物質的研究, 如對應的兩腿自旋梯子模型的SrCu2O3[9]和對應的三腿自旋梯子模型的Sr2Cu3O5[10], 發現自旋梯子系統存在著緩慢衰減的反鐵磁關聯, 會隨著自旋梯子的自旋鏈條(支腿)的數目的增加, 漸漸轉變到二維系統所具有的長程關聯, 形成復雜得令人驚訝的維度過渡行為. 在這個維度過渡過程中, 自旋梯子系統自旋鏈條(支腿)的數目的奇偶性與其性質有著密切的關系, 也就是偶數自旋鏈條(支腿)系統和奇數自旋鏈條(支腿)系統的性質有著本質的不同[11]. 當系統自旋鏈(支腿)的數目越多時, 其準一維結構空間將越趨向于二維結構空間, 因而對于自旋梯子層狀類物質的探討可以為二維自旋結構物質的理解提供豐富的信息. 當對具有自旋梯子層狀類物質摻入空穴類雜質時, 系統為了能量體系最穩定, 空穴將占據自旋梯子鏈間(橫檔)兩端的格點形成空穴對, 從而可能導致超導態的出現[12, 13].

自旋梯子系統存在著很強的量子漲落, 因而絕大多數自旋梯子模型幾乎是不能嚴格求解的. 為了得到自旋梯子系統的基態, 人們相繼提出了多種數值方法來研究自旋梯子系統, 主要使用的數值方法包括有變分量子蒙特卡洛方法(VQMC)、平均場理論[14]、精確對角化方法(ED)[15]、密度矩陣重整化群方法(DMRG)[16]、張量網絡算法(TN)[6, 7]等. 如含有次近鄰相互作用(即自旋梯子系統的對角相互作用)的兩腿自旋1/2阻挫梯子系統, 人們通過多種數值方法來研究發現其具有復雜的相圖. 在梯子系統鏈間(橫檔)存在鐵磁耦合競爭的情況下, 王孝群等人[17]與Hikihara等人[18]運用DMRG進行了研究, 在Rung-Singlet (RS)相與Haldane相之間是否存在一個狹窄區域, 即Columnar dimer (CD)相, 分別給出了不同的結果. 在梯子系統鏈間(橫檔)存在反鐵磁耦合競爭的情況下, 也存在著這類情況[6]. 而對于基于矩陣乘積態(MPS)的自旋梯子系統的張量網絡算法來說, 可以通過弦序參量來研究自旋梯子系統的量子相變和量子臨界現象, 解決此類問題, 其所模擬的系統結果將有著有著相當高的精度和相當快的效率.

本文基于張量網絡算法的自旋梯子系統的弦序參量, 來研究刻畫系統的量子相變, 從而得到相應的量子系統相圖. 對于自旋梯子系統來說, 張量網絡算法能夠模擬生成基態波函數, 從而可以計算系統可能存在的非局域序參量, 來探測自旋梯子系統的量子相變點, 以及自旋梯子系統的量子相圖[6,19-21], 這為我們提供了一個研究自旋梯子系統的量子多體物理性質強有力的工具. 為了說明這個方法, 本文研究了兩腿與三腿Staggering dimerization (SD)海森堡自旋梯子模型, 通過張量網絡算法得到的基態波函數, 來研究系統存在的非局域序參量, 即弦序參量, 從而來說明自旋梯子系統的張量網絡算法是有效的, 運用非局域的弦序參量來探測自旋梯子系統的量子相變和量子臨界性是成功的.

2 弦序參量

如果系統沒有破壞任何對稱性, 或系統缺乏相關的局域序參量, 或者系統不存在朗道對稱性破缺序, 為了更好地理解系統所涉及量子態的內稟序, den Nijs和Rommelse引入了所謂的拓撲弦序參量[22-24]的概念, 來完整地研究一些缺乏局域序的拓撲量子相變的量子系統. 系統沒有破壞任何對稱性的一些非局域的拓撲弦序參量, 會通過對偶變換, 成為類似于系統的局域序參量的形式, 這也給傳統意義上的朗道對稱性破缺序的相變理論帶來一些豐富和發展.

對于缺乏傳統意義上的局域序參量的自旋梯子系統的某些相, 如Rung-Singlet相中, 系統鏈間上格點自旋反向形成成對自旋單態, 其乘積可以直接看成基態波函數的表示. 系統的激發態有能隙, 其關聯函數呈指數性衰減, 故Rung-Singlet相的基態沒有破壞任何對稱性, 所以缺乏局域序參量, 而是存在非局域的弦序序參量. 對于自旋梯子系統的Haldane相, 鏈間上格點自旋同向, 由兩個自旋1/2形成一個自旋1的自旋三態, 其局域自旋三態的乘積可以直接看成基態波函數的表示. 因此, Haldane相與Rung-Singlet相都可以通過非局域序參量(弦序參量)來進行刻畫, 其在本質上完全相同. 這里, 定義自旋梯子系統的弦序參量為

(1)

對于自旋梯子系統來說, 其傳統意義上的局域序參量能夠由基態波函數得到的約化密度矩陣讀出, 如果系統不存在傳統意義上的朗道對稱性破缺序, 而存在非局域的弦序參量, 那么其能夠從式(1)得到.

3 理論模型與數值模擬

3.1 兩腿Staggering dimerization(SD)自旋梯子模型

無限長自旋1/2兩腿SD自旋梯子模型的哈密頓量為

(2)

其中,Si,α為作用在第α條自旋鏈條(支腿)的第i個格點上的Pauli算符.J表示在鏈間(橫檔)上的耦合系數.Ji,α表示在第α條自旋鏈條(支腿)的第i個格點與第i+1個格點之間的耦合系數, 按照i+α奇偶性進行交錯取值,Ji,α=1+(-1)i+αδ, 如圖1.

圖1 兩腿SD自旋1/2海森堡自旋梯子示意圖. 系統具有沿腿方向平移兩個格點不變性. 其中Ji,α為沿腿方向最近鄰耦合常數, J為橫檔上耦合常數.Fig. 1 Generalized infinite two-leg SD spin ladders with exchange interaction constants Ji,α and J along the leg and rung directions, respectively.

本文研究的無限長兩腿SD自旋梯子模型, 耦合系數為Ji,α=1+(-1)i+αδ,Ji,α隨δ改變而改變,即i+α為奇數與i+α為偶數時,Ji,α取值會有差異. 在圖1中, 當i+α為奇數時,Ji,α=J1,2; 當i+α為偶數時,Ji,α=J1,1. 考慮dimerization發生沿自旋梯子的兩條鏈條(支腿)方向上, 給定一個δ值, 選擇系統鏈間(橫檔)上的耦合系數J作為控制參量. 對于這樣的(δ,J)取值, 很容易得出無限長兩腿SD海森堡自旋梯子的性質[16]: (i)δ=1時, 此自旋梯子系統是交錯二聚物梯子系統; (ii)δ=0,J>0時, 此自旋梯子系統是兩條相同自旋鏈條耦合的有能隙的海森堡系統; (iii)δ=0,J=0時, 此自旋梯子系統退化成兩條沒有耦合的無能隙的海森堡自旋鏈.

通過基于矩陣乘積態(MPS)的自旋梯子系統的張量網絡算法, 給定一個δ值, 選取自旋梯子模型鏈間(橫檔)上的耦合系數J, 作為控制參量來進行計算機模擬, 得到自旋梯子系統的基態波函數, 根據系統的約化密度矩陣, 發現系統不存在朗道對稱性破缺序, 也就是說自旋梯子系統沒有局域序參量, 我們通過應用非局域的奇偶弦序參量來探測量子相變點, 得到系統相圖. 對于兩腿SD自旋1/2梯子系統, 奇弦序參量Oodd與偶弦序參量Oeven可以由式(1)計算得到. 一般地說, 通過計算奇弦序參量Oodd與偶弦序參量Oeven, 可以確定這個相為Rung-Singlet相還是Haldane相.

圖2 兩腿梯子系統奇弦序參量的計算示意圖. 紅色實線方框表示或作用, 黑色虛線方框表示作用. (i)abcd單位元胞的AB結構; (ii)abcd單位元胞的AA結構; (iii)badc單位元胞的BA結構; (iv)badc單位元胞的BB結構. 其中和是轉移矩陣E1的最大左、右本征矢量,和是轉移矩陣E2的最大左、右本征矢量.Fig. 2 Sketch of calculation of odd string order parameters in the two-leg spin ladder system.

圖3 兩腿梯子系統偶弦序參量的計算示意圖. 紅色實線方框表示或作用, 黑色虛線方框表示作用. (i)abcd單位元胞的AB結構; (ii)abcd單位元胞的AA結構; (iii)badc單位元胞的BA結構; (iv)badc單位元胞的BB結構. 其中和是轉移矩陣E1的最大左、右本征矢量,和是轉移矩陣E2的最大左、右本征矢量.Fig. 3 Sketch of calculation of even string order parameters in the two-leg spin ladder system.

選擇系統數值模擬截斷維數為D=6, 經過計算,AA結構的弦序參量Oodd、Oeven與BB結構的弦序參量Oodd、Oeven數值均為0;AB結構的弦序參量Oodd、Oeven與BA結構的弦序參量Oodd、Oeven數值分別相同, 如圖4所示. 原因在于, 具有平移兩個格點不變性的兩腿梯子模型, 存在著特定對稱性, 即在交換兩自旋鏈的同時, 加上沿自旋鏈方向平移一個格點的一并操作下, 模型具有不變性, 所以不管選擇哪一種單位元胞來計算奇弦序參量Oodd與偶弦序參量Oeven, 都能得到完全相同的值.

在圖4中, 對于兩腿SD海森堡自旋1/2梯子系統, 畫出了δ=0.4,J作為控制參數時的奇弦序參量Oodd和偶弦序參量Oeven. 我們選擇系統格點j-i為奇數, 這時Oodd和Oeven為系統的弦序參量. 當J<1.03時, 自旋梯子系統只有Oodd≠0和Oeven=0, 顯示這是Haldane相; 而當J>1.03時, 自旋梯子系統只有Oodd=0和Oeven≠0, 顯示這是Rung-Singlet相; 當然當J=1.03時, 系統有Oodd=0和Oeven=0. 此時弦序參量為連續的, 說明系統相變是連續相變, 當增大截斷維數D時, 連續相變點Jc=1.03保持不變.

圖4 兩腿自旋梯子系統的弦序參量Oodd與Oeven. 這里, 截斷維數為6.δ=0.4時, Jc =1.03為連續相變點.Fig. 4 The string order parameters Oodd and Oeven for the two-leg spin ladder as a function of J at δ=0.4. The phase transition takes place at Jc =1.03. Here, the truncation dimension is 6.

圖5 兩腿SD自旋梯子系統的(δ,J)相圖. 分別對應著RS相與Haldane相.Fig. 5 The phase diagram of the two-leg spin ladder with staggering dimerization in the (δ,J) plane. These are the RS and Haldane phases.

3 .2 三腿SD海森堡自旋梯子模型

研究的無限長三腿SD海森堡自旋梯子模型的哈密頓量為

(3)

其中,Si,α為作用在第α條自旋鏈條(支腿)的第i個格點上的Pauli算符;J為在相鄰鏈間(橫檔)上的耦合系數;Ji,α為在第α條自旋鏈條(支腿)上的第i個格點與第i+1個格點之間的耦合系數,Ji,α=1+(-1)i+αδ, 如圖6所示.

圖6 三腿SD海森堡自旋梯子示意圖. 系統具有沿腿方向平移兩個格點不變性, 其中Ji,α為沿腿方向最近鄰耦合常數, J為橫檔上耦合常數.Fig. 6 Generalized infinite three-leg SD spin ladders with exchange interaction constants Ji,α and J along the leg and rung directions, respectively.

本文研究的無限長三腿SD海森堡自旋梯子模型的耦合系數Ji,α=1+(-1)i+αδ, 隨δ改變而改變.無限長三腿SD海森堡自旋梯子模型和上文中研究的兩腿SD自旋梯子模型的性質有著一些不同[25]: (i)δ=0時, 此系統變為三條相同的自旋鏈條且沒有dimerization的無能隙的海森堡梯子; (ii)δ=1時, 此系統變成三條相同的相互交錯二聚物的自旋鏈; (iii)δ≠0,J≠0時, 此系統中的交錯二聚物相, 除了在臨界點處沒有能隙之外, 其它情況都是有能隙的. 近來人們用DMRG對δ≠0,J≠0這樣的參數取值條件, 進行了研究[25,26].

通過基于矩陣乘積態(MPS)的自旋梯子系統的張量網絡算法, 給定一個δ值, 以相鄰鏈間(橫檔)上的耦合系數J為控制參量, 來進行計算機模擬而得到系統的基態波函數. 根據系統的約化密度矩陣, 發現系統同樣不存在朗道對稱性破缺序, 我們同樣可以通過應用非局域的奇偶弦序參量來探測量子相變點, 區分不同的相, 得到系統相圖.

選擇系統數值模擬截斷維數為D=6, 經過計算, 如圖9所示,AB結構的弦序參量Oodd、Oeven(上圖)與BA結構的弦序參量Oodd、Oeven(下圖)數值分別不一致. 而AA結構的弦序參量Oodd、Oeven與BB結構的弦序參量Oodd、Oeven數值均為0. 這一點與上文中研究兩腿SD海森堡梯子系統的結果不一樣. 這是因為對于此自旋梯子系統, 交換第一條與第三條這兩條自旋鏈, 中間的那條自旋鏈保持不變, 與此同時在沿自旋鏈方向平移一個格點一起進行操作, 這時自旋梯子系統不會再保持不變性, 因而此自旋梯子系統弦序參量Oodd與Oeven數值會有兩個結果.

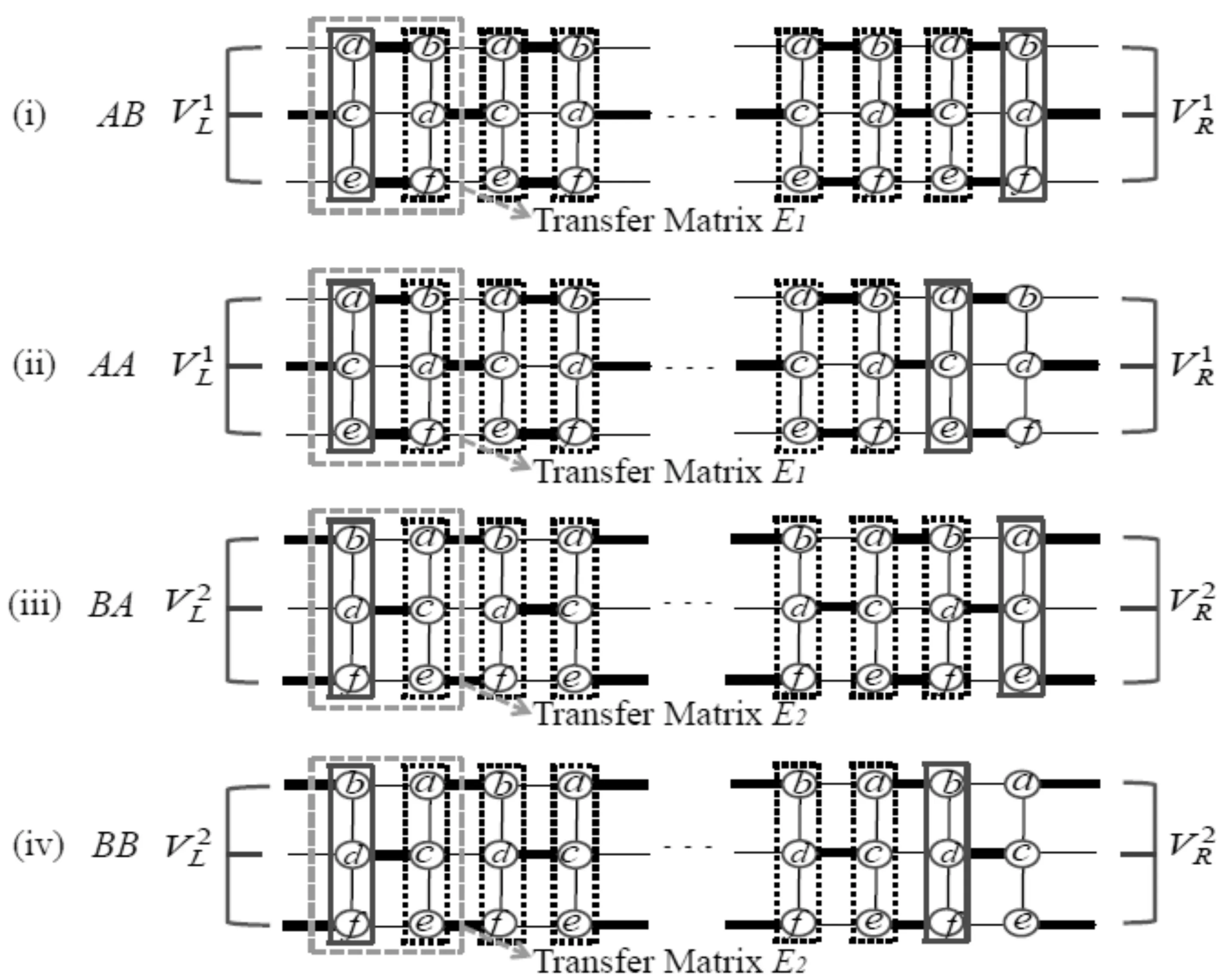
圖7 三腿梯子系統奇弦序參量的計算示意圖. 紅色實線方框表示或作用, 黑色虛線方框表示作用. (i)abcdef單位元胞的AB結構; (ii)abcdef單位元胞的AA結構; (iii)badcfe單位元胞的BA結構; (iv)badcfe單位元胞的BB結構. 其中和是轉移矩陣E1的最大左、右本征矢量,和是轉移矩陣E2的最大左、右本征矢量.Fig. 7 Sketch of calculation of odd string order parameters in three-leg spin ladder system.

圖8 三腿梯子系統偶弦序參量的計算示意圖. 紅色實線方框表示或作用, 黑色虛線方框表示作用. (i)abcdef單位元胞的AB結構; (ii)abcdef單位元胞的AA結構; (iii)badcfe單位元胞的BA結構; (iv)badcfe單位元胞的BB結構.Fig. 8 Sketch of calculation of even string order parameters in three-leg spin ladder system.

在圖9中, 對于三腿SD海森堡梯子系統, 畫出了δ=0.4,J作為控制參數時的弦序參量Oodd和Oeven. 我們選擇系統格點j-i為奇數, 這時Oodd和Oeven為系統的弦序參量. 對于選擇“abcdef”元胞即AB結構, 圖9(上圖)所示, 當橫檔耦合系數J<0.80時, 弦序參量Oodd≠0和Oeven=0, 類似于Haldane相; 當橫檔耦合系數J>0.80時, 弦序參量Oodd=0和Oeven≠0, 類似于RS相. 對于另一種選擇“badcfe”元胞即BA結構, 圖9(下圖)所示, 當橫檔耦合系數J<0.80時, 弦序參量Oodd=0和Oeven≠0, 類似于RS相; 當橫檔耦合系數J>0.80時, 弦序參量Oodd≠0和Oeven=0, 類似于Haldane相. 但不管怎么選擇AB結構或BA結構, 都能發現當橫檔耦合系數J=0.80時, 弦序參量Oodd=0和Oeven=0, 這說明三腿SD海森堡梯子系統在δ=0.4時, 其相變點在Jc=0.80, 為連續相變. 當增大截斷維數D時, 系統量子相變點Jc與弦序參量幾乎沒有漂移. 在圖9中, 我們注意到當選擇元胞abcdef時, 獲得的奇弦序參量Oodd與文獻[25,26]中由DMRG方法計算出來的奇弦序參量值幾乎一致.

圖9 三腿SD自旋梯子系統的弦序參量Oodd與Oeven. 這里, 兩種不同的元胞選擇(上圖與下圖)都顯示在截斷維數為6時,Jc=0.80為連續相變點.

Fig. 9 The string order parametersOoddandOevenfor the three-leg spin ladder with staggering dimerization as a function ofJatδ=0.4. Here, the top and the bottom panels correspond to two different choices of the unit cell for the ladder system, respectively. For both choices, the phase transition point is located atJc=0.80. The truncation dimension is 6.

圖10 三腿SD自旋梯子系統的(δ,J)相圖.Fig. 10 The phase diagram of the three-leg spin ladder with staggering dimerization in the (δ,J) plane.

本算法應用于三腿梯子系統與兩腿梯子系統, 同樣是收斂的, 同樣可以得到基態. 對于本文中的三腿梯子系統具有平移兩個格點不變性, 所以弦序參量是有兩種選擇方式, 而這兩種選擇方式所計算出來的奇偶弦序的值恰恰是不同的.

4 結 論

近幾年, 張量網絡算法成為在數值計算領域中的研究強關聯電子量子格點系統最為重要的算法, 是基于張量網絡表示的高效的數值模擬算法. 人們一直在發展和優化, 以盡可能的利用有限的計算資源, 直接對熱力學極限下的量子強關聯系統進行最大程度的數值模擬. 本文通過基于矩陣乘積態(MPS)的自旋梯子系統的張量網絡算法, 摸索研究自旋梯子量子多體系統的弦序參量,探測系統的量子相變點, 刻畫系統的量子臨界現象, 獲取系統的量子相圖, 這為我們提供了一個研究自旋梯子系統的量子多體物理性質強有力的工具和方法: 在不知道系統是否缺乏朗道對稱性破缺序或者系統是否存在相關的拓撲弦序的情況下, 可以先得到系統的基態波函數, 如果基態缺乏朗道對稱性破缺序, 或者通過另外方式找出系統存在若干非局域的弦序參量, 來完整地描述一些拓撲量子相變點, 獲得系統的量子相圖, 從而豐富和發展了傳統的朗道對稱性破缺的相變理論.