可傾瓦推力軸承潤滑油膜靜動特性計算的嵌套式二分法與應用

李賢燚，趙 耀

（華中科技大學 船舶與海洋工程學院，武漢 430074）

0 引 言

對艦船推進軸系縱向振動的傳統研究中，研究者將推進軸系的縱向振動等同于桿的縱向振動，忽略了推進軸系的轉子特征，缺乏對推力軸承潤滑油膜軸向動特性的定量研究。推進軸系是典型的轉子—軸承系統，由軸系轉子和軸承非轉子兩部分組成。轉子的重要特征是潤滑，這是與桿等非轉子結構的顯著區別所在。軸承內部推力環和推力瓦之間的動壓潤滑油膜起承載和傳遞螺旋槳推力的作用，當推力環在螺旋槳脈動推力激勵下發生縱向振動時，推力環在其平衡位置前后擠壓潤滑油膜，使潤滑油膜內產生壓力脈動，進而表現出動特性。顯然，在推進軸系縱向振動過程中，潤滑油膜的動特性是客觀存在的。這種動特性因推進軸系縱向振動而產生，必然反作用于推進軸系，對其縱向振動特性和力傳遞特性產生一定影響。盡管推力軸系縱向振動分析需借助于桿縱向振動的基本理論，但必須將潤滑油膜動特性反映在動力學模型中。在認識到潤滑油膜影響推進軸系縱向振動特性的客觀性后，要具體說明其影響程度。具體回答這個問題，必須對潤滑油膜動特性進行定量研究，將計算結果作為推進軸系縱向振動分析模型的數據輸入，通過比較有無潤滑油膜動特性的計算結果確定潤滑油膜的影響。通過潤滑油膜動特性架起轉動與縱向振動的連接“橋梁”，進而可以解釋推進軸系縱向振動隨轉速變化的動頻特性，分析追蹤軸系縱振低頻線譜產生的原因。

隨著潤滑理論的完善和計算機的應用，可傾瓦推力軸承潤滑油膜的靜動特性的研究，從一維流模型：推力瓦的一邊無限長簡化或無限短簡化；到二維流模型：考慮實際推力瓦的結構尺寸；再到三維模型：考慮油膜厚度方向上特性的變化。Schwanecke[1]和Vassilopoulos[2]對推力軸承潤滑油膜軸向剛度和阻尼的計算開展了早期的探索。Purday[3]通過對大量不同瓦塊形狀所做的研究發現，進口和出口間的油膜楔形并不重要，重要的是油膜厚度比值的大小。Srikanth等[4]建立了大型可傾瓦推力軸承剛度系數和阻尼系數模型。Almqvist等[5]對可傾瓦推力軸承展開THD分析，并做了實驗驗證。Zhang等[6]較早在船用推進軸系中采用二維流計算方法，在潤滑特性分析的基礎上，計算出油膜動特性及其對軸系縱向振動的影響。溫詩鑄、楊沛然等[7-8]總結和完善了潤滑理論。李忠等[9]對可傾瓦推力軸承的線性和非線性動特性作了研究。黃斌等[10]對推力軸承三維熱彈流性能及其振動噪聲特性進行了分析研究。上海交通大學機械系統與振動國家重點實驗室李棟梁等[11]利用有限差分法進行數值計算得到了油膜的壓力分布和油膜阻尼和剛度隨轉速的關系。

本文在前人的基礎上，創新性地提出“嵌套式二分法”數值算法求解潤滑油膜靜特性，在得到油膜的壓力、溫度和厚度分布的基礎上，再利用泰勒級數展開法將壓力展開式代入瞬態雷諾方程進行求解得到推力軸承的軸向動特性系數。根據軸系試驗的結果，對本文數值計算得到的動特性趨勢進行了驗證。

1 油膜特性分析理論模型

1.1 靜特性分析模型

二維流動壓潤滑理論以實際有限寬扇形推力瓦為潤滑油膜載體，其控制方程包括雷諾方程、能量方程、膜厚方程和粘度—溫度方程。潤滑油膜靜特性的分析就是對這些控制方程的聯立求解,得到潤滑油膜壓力分布、溫度分布等。

（1）穩態雷諾方程

Reynolds方程是由運動方程和連續方程推導出，是流體潤滑理論最基本的方程。在本文研究的可傾瓦推力軸承中，為方便分析，建立柱坐標形式下的Reynolds方程：

式中：左端表示潤滑膜壓力在潤滑膜表面上隨徑向r和周向θ的變化，右端表示潤滑油膜的動壓效應，即可傾瓦傾斜造成的壓力變化，ω為角速度。

（2）能量方程

對于分析流體潤滑，由于每塊推力瓦從入口到出口潤滑油膜的動能和勢能變化很小，可以忽略掉，潤滑油能量的變化僅為溫度的函數。根據功能關系建立起絕熱條件下，潤滑油膜能量方程的柱坐標形式：

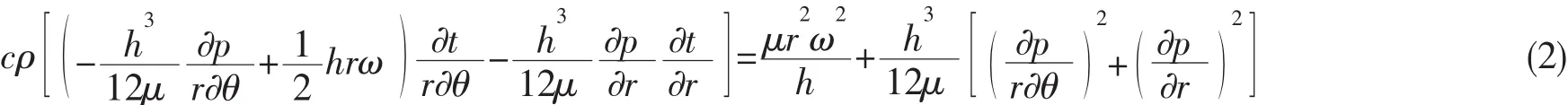
（3） 膜厚方程

對于線支撐推力軸承可傾瓦，支撐線為OP，根據結構幾何關系可得到推力軸承鏡板和可傾瓦之間的油膜厚度方程為：

式中：hp為推力瓦支撐中心的油膜厚度，γp為可傾瓦的周向傾斜角。一般地，γp很小，有tanγp≈γp。若可傾瓦為點支撐，厚度方程中加入徑向傾角對油膜厚度的影響項即可。

（4）粘度—溫度方程

潤滑油膜的粘度是影響潤滑性能的核心因素。ASTM（美國材料試驗協會）研究表明，通常對礦物油，粘溫關系滿足：

式中：υ為潤滑油運動粘度，a，b為常數。

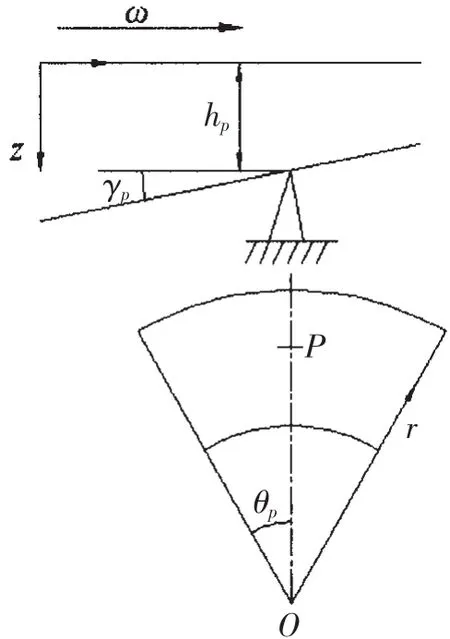
圖1 可傾瓦結構示意圖Fig.1 Geometry of tilting pad

1.2 動特性分析模型

對推力軸承的振動傳遞特性分析的關鍵是要得到潤滑油膜的動特性，在已知油膜靜特性的基礎上，本文通過對雷諾方程的壓力項進行泰勒級數展開，然后將得到的壓力微分項代入剛度、阻尼表達式，求得潤滑油膜的軸向動特性系數。

推力軸承在軸向脈動力的作用下，使得潤滑油膜隨著推力環在平衡位置附近振動，油膜壓力也因此在一個微小的范圍內波動，這也正是潤滑油膜表現出動特性的原因。油膜厚度的擾動引起油膜壓力的擾動，故油膜壓力為推力環軸向波動位移及其增量的函數，根據二元函數泰勒展開[12]：

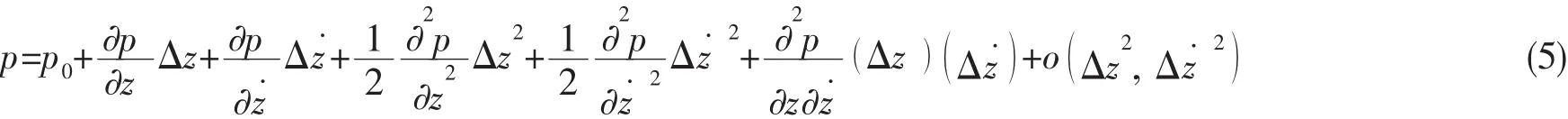
在保證計算精度的前提下，為了方便計算忽略掉高階小量：

將（6）式在推力瓦上面積分，可得：

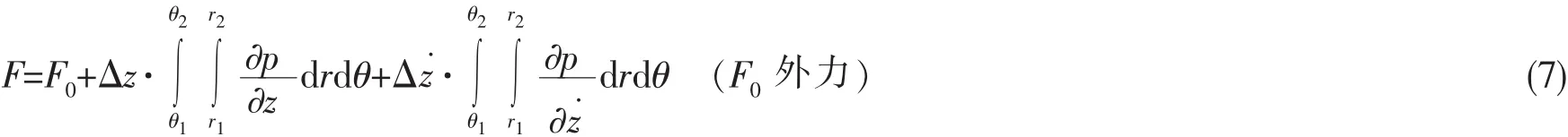
由剛度、阻尼的定義可知：

要通過上式計算出剛度系數和阻尼系數，必須先得到兩個壓力微分項。在油膜動特性分析模型中，油膜滿足瞬態雷諾方程：

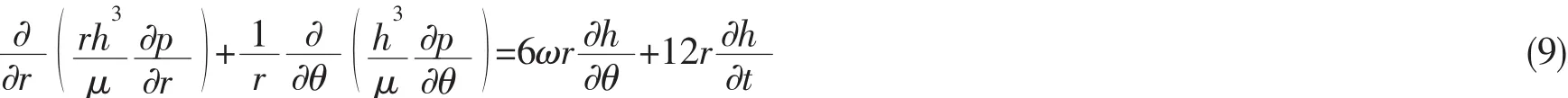
式中右端第二項是由于在脈動推力的作用下，推力環縱向振動，對潤滑油膜的擠壓效應。

將壓力泰勒展開項代入雷諾方程中，同時

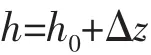
式中：h0為平衡狀態下油膜厚度，Δz為油膜振動引起的厚度變化量。得到：

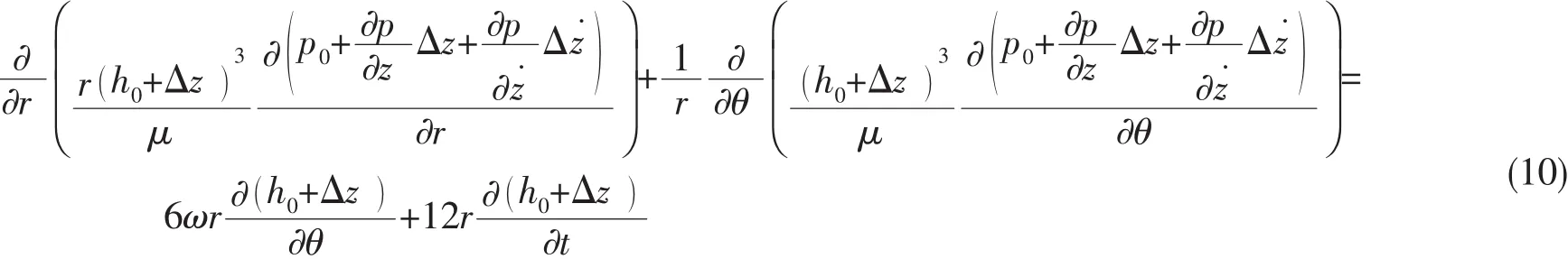
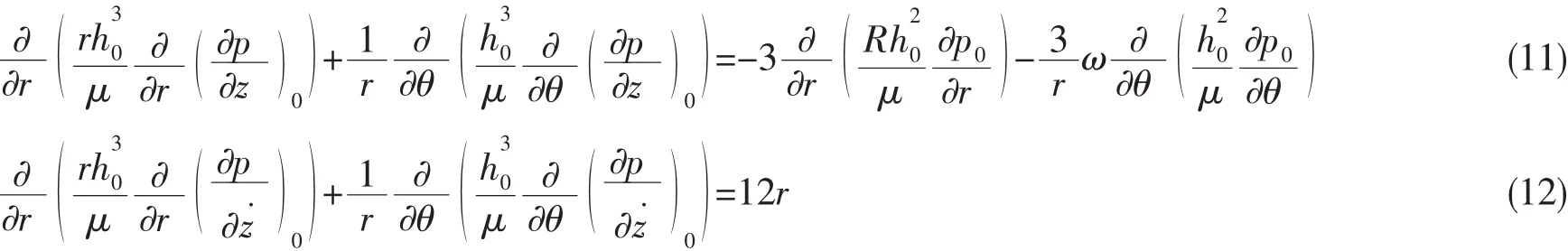
2 嵌套式二分法數值計算

建立了可傾瓦推力軸承潤滑油膜的靜動特性理論模型之后，本文在有限差分法的基礎上，通過對該問題的數學模型的分析，提出嵌套式二分法，數值求解得到潤滑油動態性系數。

首先為了更好地描述潤滑靜動特性客觀規律和方便利用微積分等數學工具進行處理，須將各控制方程無量綱化。對于油膜靜特性控制方程，可分別取推力瓦寬度b，支撐點油膜厚度hp，初始粘度μ0，初始油溫t0，角速度ω為基準量。

各控制方程的無量綱方程分別為：

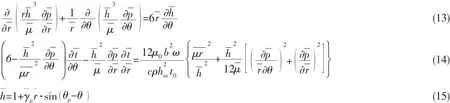
2.1 離散無量綱方程

控制方程中雷諾方程和能量方程都是偏微分方程，且推力瓦屬于規則形狀，故采用有限差分進行離散。

（1）雷諾方程的離散

雷諾方程為二維偏微分方程，其離散結果如下：

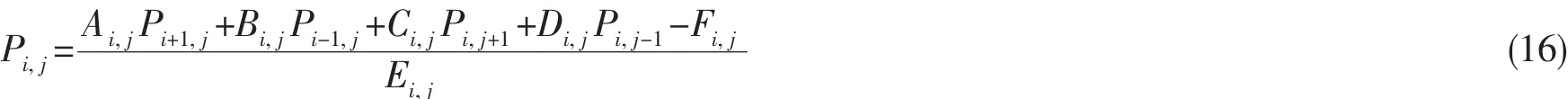
式中：各系數分別為

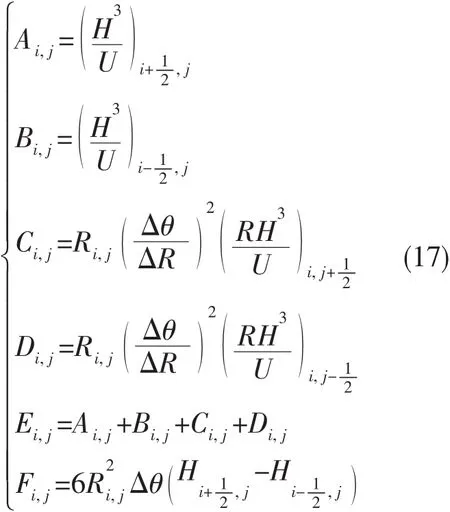
壓力場計算的收斂準則定義為：

圖2 潤滑油膜有限差分網格Fig.2 The finite difference method grid of lubricating oil film

初次計算時，可令全部油膜節點壓力值為零。通過（16）式反復迭代，若第k次與第k-1次油膜壓力值滿足收斂條件，則終止迭代過程，得到無量綱油膜壓力收斂值，量綱化后可得油膜壓力分布。

（2）能量方程的離散

能量方程是關于溫度和壓力的偏微分函數，潤滑油膜溫度場的求解必須先已知其壓力場。潤滑油在供油溫度下進入楔形間隙，此后潤滑油膜溫度隨流動過程逐漸變化，故溫度場的求解可歸結于初值問題，而初值問題的數值計算可采用步進方法。其離散結果如下：

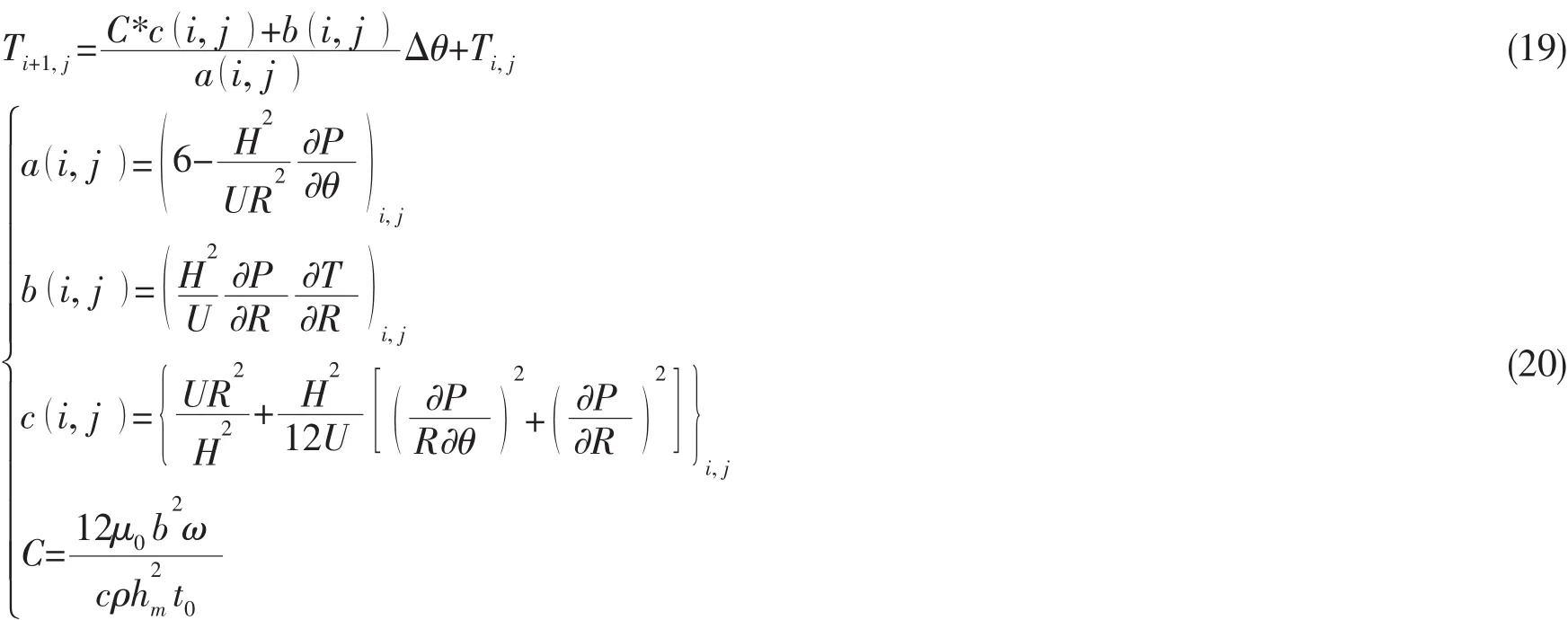
能量場的求解實際上是求解穩定溫度場，在可傾瓦入口處為第一類邊界條件t（ r,0 ），在為第二類邊界條件

溫度場計算的收斂準則定義為：

2.2 動特性方程的數值計算

動特性控制方程（11）、（12）與雷諾方程的形式相同，可按照同樣的方法進行無量綱化和離散，數值求解出壓力微分項的分布。將（8）式無量綱化，容易推導出帶量綱剛度阻尼系數和無量綱剛度阻尼系數的關系為

2.3 計算流程圖

為了更好地反應嵌套式二分法的計算流程，本文采用不同于常規的流程圖[13]：

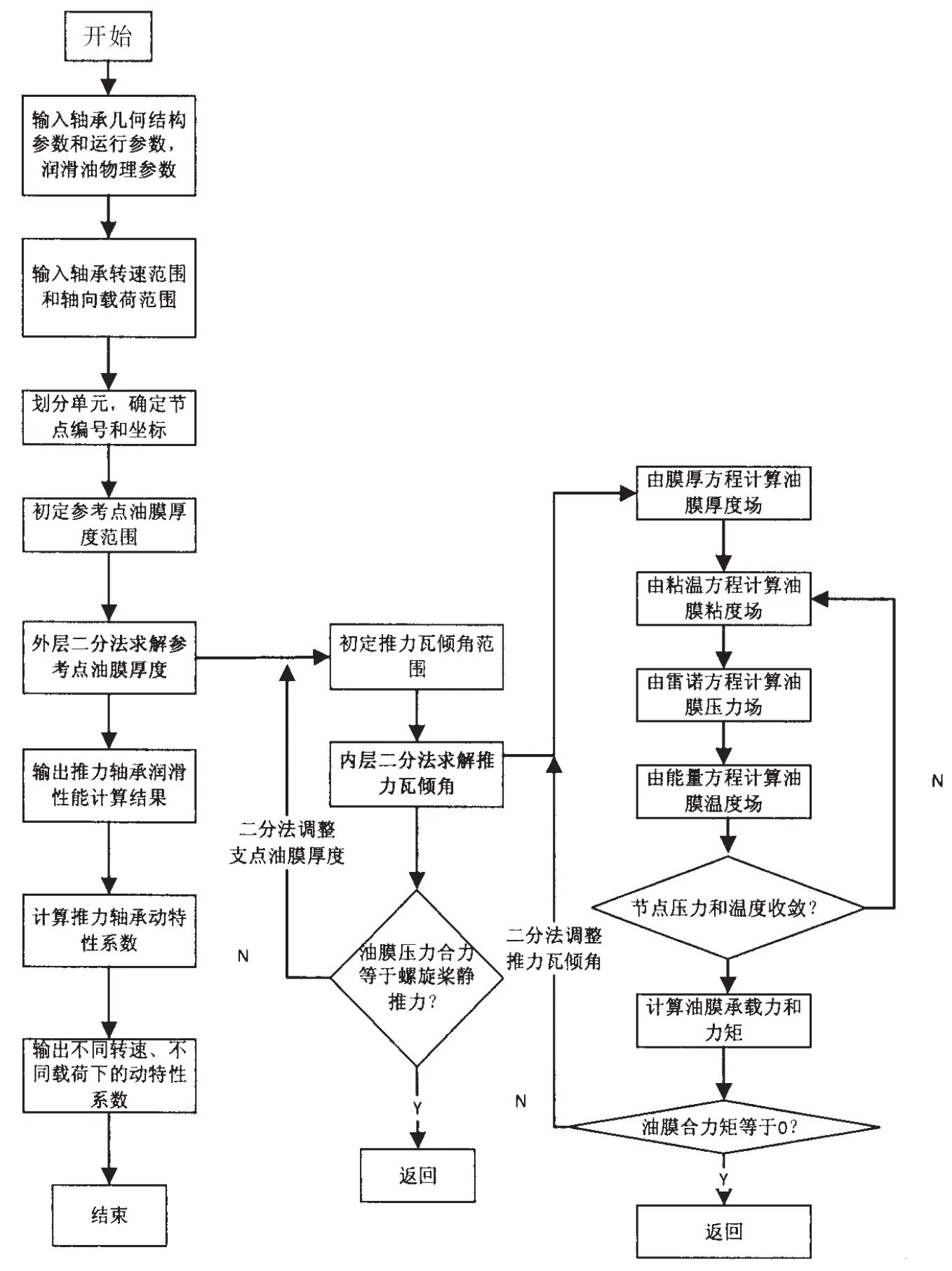
圖3 動壓潤滑靜動特性數值計算流程框圖Fig.3 Numerical calculation flow diagram of lubrication static and dynamic characteristics

推力瓦及潤滑油膜在工作狀態下必定是處于某個穩定平衡狀態，在這個穩定狀態下油膜的承載力等于外界載荷，可傾瓦力矩平衡。分析潤滑特性問題的核心就是求解穩定狀態下推力瓦的形態，而推力瓦的形態可由推力瓦傾角和參考點油膜厚度兩個參數確定，這里選用支撐中心處的油膜厚作為參考點油膜厚度。由圖3知，確定了推力瓦形態之后也同時得到油膜的壓力分布、溫度分布和厚度分布。因為油膜承載力和油膜合力矩都是推力瓦傾角和參考點油膜厚度的抽象函數，推力瓦形態的求解抽象為以下方程組的數值求解：

“中國市場是民族企業的根，把根維護好有助于企業的良好發展，但如果想要擴大品牌影響和企業實力，海外市場是檢驗民族企業的真正考場。”畢總說，“如今，比亞迪叉車已經在海外市場取得了一定成功，如在歐美市場，比亞迪叉車與來自德國、美國、日本等眾多知名品牌同臺競技，不僅沒有依靠價格優勢去占領市場，反而因為在鋰電領域的技術優勢，獲得了極好的市場認可度和保有量，市場能有這樣的反應，用兩個字概括——便是‘品質’。”

由于數學模型是關于厚度和傾角的抽象函數，而參考點油膜厚度和推力瓦傾角又有且僅有一個值，因此可以在二分法數值求解的基礎上發展嵌套式二分法來計算，然后再在此基礎上計算潤滑油膜動特性。即算法外層采用二分法計算油膜承載力，內層采用二分法計算油膜合力矩，從而計算出讓油膜合力矩為零、承載力等于螺旋槳靜推力的參考點油膜厚度值和推力瓦傾角值。

嵌套式二分法相對于傳統算法來說主要有三大優點：

（1）在傳統算法中，參考點油膜厚度和推力瓦傾角對計算遞進選取的計值依賴度較高，若遞進值過大，則有可能得不到想要的計算結果；而嵌套式二分法只要真實解在給定的初始區間中，就一定能夠以較快的速度得到理想的結果。

（2）其次是計算效率上，嵌套式二分法的效率相對于傳統算法有大幅度提高，這一點主要是由于嵌套式二分法算法本身的特點決定的。

（3）對于給定初始區間上，傳統算法對初始區間比較敏感，若初值選擇得不合適可能導致迭代的效率很低，甚至是發散的，而嵌套式二分法在理論上可以不依賴初始區間，當然考慮到計算效率，可以調整更合適的計算區間，提高計算效率。

3 嵌套式二分法的應用

本文利用嵌套式二分法數值計算結果去解釋軸系振動試驗現象，從而驗證嵌套式二分法的正確性。

3.1 船舶軸系實驗

設計如圖所示軸系試驗臺,然后進行振動測試，得到以下各實驗測點的頻響函數。在實驗中，由于條件的限制，對于不同轉速，軸向載荷固定不變。下面以試驗臺基座測點為例來說明實驗結果。

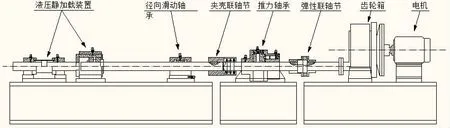
圖4 軸系試驗臺結構Fig.4 Structure of the thrust bearing system test rig

圖5 軸系試驗臺實物Fig.5 Photograph of the thrust bearing system test rig

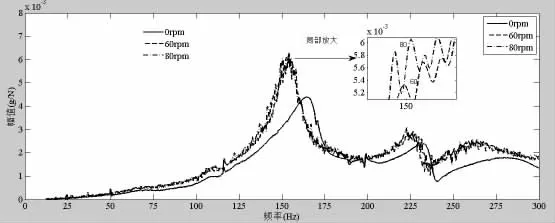
圖6 試驗臺基座測點（g表示加速度響應單位）Fig.6 Measure point of test rig foundation

從實驗得到的頻響函數曲線可以看出，當轉速為0時，幅值最低，且遠低于有一定轉速時的幅值；轉速為60 rpm和80 rpm時，兩者幅值比較接近，前者的幅值略低于后者。

3.2 數值計算結果

以實驗軸系的推力軸承為算例，采用嵌套式二分法程序進行數值計算首先得到潤滑油膜靜動特性。

（1）靜特性分析結果

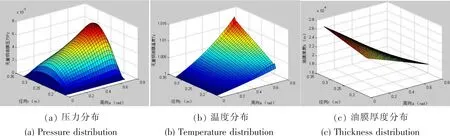
圖7 靜特性結果Fig.7 The results of static characteristics calculation

從壓力分布圖可以看出，最大壓力所在位置更靠近可傾瓦出口處，這符合質量守恒定律，楔形油膜的流動是剪切流動和壓力流動共同作用的結果。從溫度分布圖可以看出，沿著潤滑油膜流動的方向，由于摩擦生熱的累積效應溫度逐步上升。油膜厚度分布圖反應了可傾瓦在穩定狀態下的工作形態。

（2）動特性分析結果

根據上文的數值計算方法，得到了油膜剛度、阻尼隨轉速的變化規律，同時得到在這個狀態下的各點油膜厚度和可傾瓦傾角。為了解釋軸系振動試驗中得到的頻響函數變化規律，本文僅呈現計算得到的剛度隨轉速的變化。

船用推力軸承潤滑油膜最初的分析方法來自渦輪機機組推力軸承,由于兩者在功能上有一定的區別，渦輪機推力軸承主要是承受發電機轉子和渦輪機轉子的重量以及水流產生的全部推力，而船用推力軸承是傳遞螺旋槳傳來的隨轉速變化的推力。同時也考慮到軸系實驗條件的特殊性。所以此處分別計算轉速和載荷獨立與非獨立時，潤滑油膜動特性與轉速的關系。

當轉速與載荷為分獨立變量時（載荷恒定100 kN）：

從圖8可知，在載荷不隨轉速變化的情況下，隨著轉速的增加，潤滑油膜的剛度逐漸減小。而又根據振動微分方程：

式中：m、c、k分別代表振動系統的質量、阻尼、剛度，F0為外力幅值，ω為外力的激勵頻率。設為穩態相應的復振幅，，代入有，則得到幅頻響應函數：

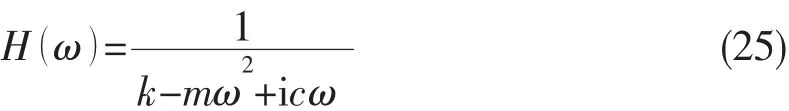
式中：剛度k和阻尼c的變化趨勢是相同的，并且k的數量級要高于c，因此隨著剛度的增加頻響函數幅值H（ω）減小。

由（25）式和圖8可知，隨著轉速的增加，油膜剛度系數減小，進而頻響函數幅值增加。對于軸系振動試驗的結果（圖6），當轉速為0時，潤滑油膜沒有參與軸系串聯系統的振動，因此振動系統的剛度是最大的，而當潤滑油膜參與軸系振動時，隨著轉速從60 rpm增加到80 rpm，潤滑油膜的剛度略微減小，因而振動系統的剛度也減小，頻響函數的幅值稍稍增大。 這說明通過嵌套式二分法數值計算的結果與實驗現象相符合,也驗證了該方法的可行性。

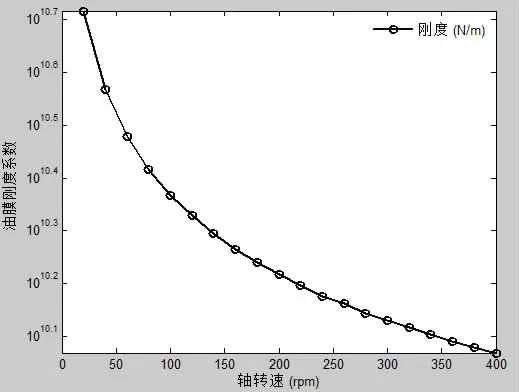
圖8 油膜剛度隨轉速變化曲線Fig.8 The oil film stiffness curve changing with speed

當轉速和載荷為非獨立變量時，螺旋槳推力和轉速的關系為[14]

式中：KT即為螺旋槳推力系數，n為螺旋槳轉速，D為螺旋槳直徑，ρ為水的密度。

由（25）式和圖9可知，隨著轉速的增加，油膜剛度系數增加，進而頻響函數幅值減小。

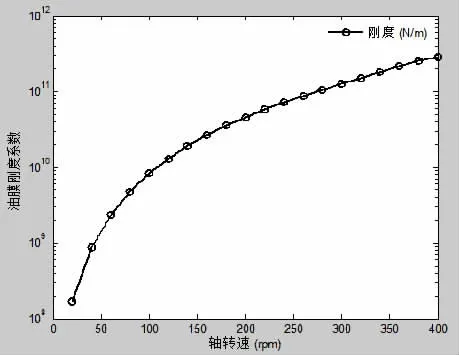
圖9 油膜剛度隨轉速變化曲線Fig.9 The oil film stiffness curve changing with speed

因此，載荷與轉速獨立和非獨立的情況下，油膜剛度隨轉速的變化趨勢是截然相反的，因此忽略船舶推進軸系載荷與轉速的關系，將會得出錯誤的結論。

4 結 論

本文在分析可傾瓦推力軸承潤滑油膜靜動特性的數學模型中提出了嵌套式二分法數值求解的方法，得到了以下結論：

（1）可傾瓦推力軸承潤滑特性是由可傾瓦形態決定的，可傾瓦的形態可由任意參考點的油膜厚度和傾角確定。

（2）嵌套式二分法與傳統計算方法相比，計算效率會更高，同時適用性更強。對于和本文研究問題的數學模型類似的情況，都可以使用嵌套式二分法來編程計算。

（3）該方法可應用于船用推力軸承，大型汽輪機、水輪機縱向推力軸承的動特性計算。只有在軸系轉速和載荷滿足螺旋槳敞水試驗的關系時，可傾瓦推力軸承潤滑油膜的剛度才隨轉速上升而增加；當載荷不隨轉速變化而變化時，可傾瓦推力軸承潤滑油膜的剛度才隨轉速上升而降低。