數學史融入初中課堂的案例研究

曾 崢，楊豫暉，李學良

?

數學史融入初中課堂的案例研究

曾 崢1，楊豫暉1，李學良2

（1．佛山科學技術學院，廣東 佛山 528000；2．佛山市南海區南海實驗中學，廣東 佛山 528000）

目前，初中數學課堂教學過于強調讓學生掌握數學內容知識和培養學生的數學推理能力，忽略了引導學生理解數學的現狀和歷史發展，以及培養學生對數學的積極態度．從長遠來看，這會導致學生對數學的片面認知，也不利于數學文化的傳承．數學史融入初中數學課堂教學的做法可以讓學生理解數學的現狀和發展歷史，培養學生對數學的積極態度．研究提供了數學史融入初中數學課堂的方法，進行了數學史融入初中課堂的案例研究，包括加深數學概念的理解，避免數學家的錯誤重現以及導入新課提高學習興趣3個方面的研究，為初中數學教師提供教學參考．

數學史；初中數學教學；教學方法；案例研究

美國數學教育家Wilkins[1]認為數學教育的目標是讓每個學生都應該：（1）掌握數學內容的知識；（2）具有數學推理能力；（3）承認數學的實用性和社會影響；（4）理解數學的現狀和歷史發展；（5）對數學有積極的態度．依此標準審視國內數學教育現狀，恐怕后兩條是最令人擔憂的．盡管新課程改革給基礎教育帶來新氣象，但是因考試的指揮棒而被動、機械學習數學的情況并未得到有效改善．

數學史融入初中數學課堂教學可以讓學生理解數學的現狀和發展歷史，培養學生對數學的興趣和積極態度．相關研究可以分為兩大類，一類研究認為數學課堂中有效滲透數學史是一種教學手段，可以培養和保持學生的數學學習積極態度．比如，Jones[2]認為，在課堂中滲透數學史可以作為一種教學手段來改善學生對數學的態度；McBride[3]發現，每節課給學生講五分鐘數學故事，可以讓學生保持對數學學習的熱情，激發學生學習動機，培養學生對數學的積極態度；Fauvel[4]積極提倡通過在課堂中融入數學史來改善學生的數學觀，培養學生對數學的積極態度；Liu Po-Hung[5]等學者呼吁一線教師需要在課堂中使用數學史來提高學生的學習動機，培養學生對數學的積極態度．另一類研究認為數學課堂教學有效滲透數學史能夠改變學習方式，提高學生的數學學業成就．比如，新加坡學者Wee Leng NG[6]發現，在初二數學課堂中滲透秦九韶的名著《數書九章》，可以極大地提高學生的數學成績和科學成績；Schiefele[7]等發現，讓學生特別是新加坡的華裔學生，學習中國古代數學家的經典作品，可以增加他們對數學的學習興趣，同時也可以提高學生的成績；Katz[8]認為，在課堂中使用數學史可以培養學生積極的學習心向，讓學生理解數學的現狀和發展歷史，提供多元的學習方式．數學史對數學教育的意義已經是許多數學教育家的共識：利用數學史可以激發學生的學習興趣，培養學生的數學精神，啟發學生的人格成長，預見學生的認知發展，促進學生對數學的理解和對數學價值的認識，構筑數學與人文之間的橋梁[9]．

那么，如何在數學課堂教學中有效滲透數學史呢？國內外學者也進行了相關研究，Jankvist[10]認為，數學史在課堂中使用的路徑分為：數學史作為教學工具和數學史作為教學目標．他認為數學史融入課堂的教學方法分為：基于歷史法、歷史啟發法和模塊教學法；學生學習數學史的方式分為：數學史工作單、模塊學習和學生學習計劃．汪曉勤[11]認為，數學史融入課堂的教學方式是：重構式、附加式、順應式和復制式．Tzanakis、ArcaviJ[12]等提出，數學史的融入方法是：提供歷史材料，討論數學話題和發展數學意識．

基于以上研究，依據北師大版《義務教育教科書?數學?七年級上》[13]的內容，精心選取對應的數學史、數學趣聞和數學文化讀物，綜合以上所提及的數學課堂滲透數學史的路徑，經過教學設計、課堂實施和課后反思形成相應案例，擬為初中數學教師提供切實的教學參考．

1 滲透數學史 掌握核心概念

如果教師把數學僅僅視作一種技能或者一件工具去傳授，這樣做縱使傳授了有關知識，亦必掩蓋了數學作為文化活動的面目[14]．數學是一門累積起來的學科，它將永遠融會于它的過去以及未來當中[14]．數學教師應該利用數學史來展示數學概念的來龍去脈，幫助學生理解數學概念的歷史和現狀，進而教師能更好傳授數學知識，學生能更好理解數學核心概念[14]．

1.1 “有理數”相關概念的教學

在“2.1有理數”的教學中，“負數”和“有理數”作為這一章的重點內容和核心概念，一直是學生學習的重點和難點．有關負數的概念，最早記載于在名著《九章算術》[15]中，書中提出了“正負術”，“術曰：如方程，各置所取，以正負術入之”．《九章算術》的第八章“方程”中，把“賣（收入錢）”作為正，則“買（付出錢）”作為負，把“余錢”作為正，則“不足錢”作為負．在關于糧谷計算的問題中，是以“益實（增加糧谷）”為正，以“損實（減少糧谷）”為負．中國數學家劉徽[15]在《九章算術》的“正負術”的注文中給出了正負數的定義：“今兩算得失相反，要令正、負以名之．”意思是說，在計算過程中遇到具有相反意義的量，要用正數和負數來區分它們．教師在課堂中講述負數的歷史，融入《九章算術》中的實例和定義，讓學生對“負數”概念的理解更加深入．在“有理數”的教學中，教師介紹有理數的起源和傳播，把“有理數”的歷史稱為“一場美麗的誤會”，來還原“有理數”概念的本來面目．通過有理數的歷史，教師可以幫助學生澄清頭腦中對“有理數”的錯誤理解，幫助學生掌握有理數的概念．

1607年，中國數學家徐光啟和西方傳教士利瑪竇（Matteo Ricci）根據克拉維烏斯的《歐幾里得原本十五卷》翻譯成古漢語的《幾何原本》[19]．在《幾何原本》[19]中，他們將有理數“proportio”翻譯為古漢語中的“理”，這里的“理”意思是“比值”，徐光啟和利瑪竇的翻譯也是忠于畢達哥拉斯學派對于“有理數”的原意來翻譯的．可是“有理數”傳播到日本的時候出現了偏差，在明治維新之前，日本關于歐洲數學的論著研究，基本上都是采用中國譯本．日本學者將中國文言文中的“理”直接翻譯成了“理”，而不是古漢語所解釋的“比值”．后來，日本學者直接用錯誤的“理”翻譯出了“有理數”，可謂差之毫厘、謬以千里．當“有理數”從日本傳回中國時又延續這個錯誤，清末中國派留學生到日本，將“有理數”傳回中國，因此現在中日兩國都用“有理數”和“無理數”的說法．可見，由于當年日本學者對中國文言文的理解不到位，才出現了“美麗的誤會”．因此，“有理數”的原意是指“成比例的數”，而不是學生想象中的“有道理的數”，教師幫助學生澄清“有理數”這一概念，可以更好地協助學生掌握有理數的概念．同時，數學教師應根據“有理數”翻譯的歷史，讓學生理解和體會“有理數”概念的歷史和現狀，引導學生深入理解數學概念的內涵．

1.2 “有理數的乘方”相關概念的教學

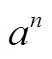
1.3 “認識一元一次方程”相關概念的教學

在金庸的《射雕英雄傳》[24]中也有講述中國古代“天元術”的精彩片段：

只見那內室墻壁圍成圓形，地下滿鋪細沙，沙上畫著許多橫直符號和圓圈，又寫著些“太”“天元”“地元”“人元”“物元”等字．黃蓉自幼受父親教導，頗精歷數之術，見到地下符字，知道盡是些術數中的難題，那是算經中的“天元之術”，雖然甚是繁復，但只要一明其法，也無甚難處（按：即今日代數中多元多次方程式，我國古代算經中早記其法，天、地、人、物四字即西方代數中X、Y、Z、W四未知數）．黃蓉從腰間抽出竹棒，倚在郭靖身上，隨想隨在沙上書寫，片刻之間，將沙上所列的七八道算題盡數解開．

這些算題那女子（瑛姑）苦思數月，未得其解，至此不由得驚訝異常，呆了半晌，忽問：“你是人嗎？”黃蓉微微一笑，道：“天元四元之術，何足道哉？算經中共有一十九元，‘人’之上是仙、明、霄、漢、壘、層、高、上、天，‘人’之下是地、下、低、減，落、逝、泉、暗、鬼．算到第十九元，方才有點不易罷啦！”那女子（瑛姑）沮喪失色，身子搖了幾搖，突然一跤跌在細沙之中……

教師將這段與方程有關的文字素材展示給學生，再播放影視作品《射雕英雄傳》中的對應片段，讓學生對“一元一次方程”的概念有更進一步的理解，對方程有更深入的體會．教師在講解“一元一次方程”概念時，借鑒“一元一次方程”的發展歷史來講解新課，使用小說素材，講述有關方程的趣事，可以提升學生的學習興趣，培養學生積極的態度．在課堂中為學生提供“一元一次方程”方程概念的來龍去脈，提供學生感興趣的與數學文化有關的小說讀物，數學課堂變得更加多彩，更具人文價值．數學教育的人文價值一直是數學教育的重要價值取向[25]，數學教師需要積極開發數學課堂的人文教育功能[26]，提高學生對數學的積極態度．

2 引入數學史 避免錯誤重現

教育家斯賓塞（Herbert Spenser）認為：兒童的教育，無論在方式上，或在安排上，均須與歷史上人類的教育相對應[27]．換言之，個人知識的發生必須遵循種族知識發生的途徑[27]．弗賴登塔爾（H. Freudenthal）強調：盡管年輕人的學習方式改變了，但年輕人的學習仍會重蹈人類的學習過程[28]．數學教師都應該學習數學史，應該在課堂中引入數學史來避免先驅的失誤在學生中重現[29]．在數學課堂教學中，教師引入數學家的錯誤和先驅的失誤，會讓學生對數學概念和運算過程更加清晰，可以有效地讓學生避免這些錯誤．在課堂教學中，教師應該讓學生重新經歷人類認識數學的重大幾步[30]，這樣的數學課堂會取得更好的教學效果．

2.1 利用數學史講透數學運算法則

在“有理數的運算”的教學中，可以引入“有理數運算法則”的歷史，讓學生對運算的法則理解得更加透徹，避免運算的錯誤．《九章算術》[15]中記載了有理數的加減法運算法則：“正負術曰：同名相除，異名相益．正無入負之，負無入正之．其異名相除，同名相益．正無入正之，負無入負之．”元代朱世杰在《算學啟蒙》[20]記載了有理數的乘除法運算法則：“同名相乘為正，異名相乘為負”，“同名相除所得為正，異名相除所得為負”．教師通過引入《九章算術》和《算學啟蒙》中有關有理數的表述，讓學生感悟有理數的運算法則，體會中國古代的數學成就，了解有理數運算法則的起源與發展．

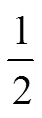
數學教育學者Arcavi[33]在課堂教學中曾經引用過有關負數歷史的例子，這個例子[34]是：“17世紀，法國數學家Arnaud（1612—1694）曾經寫過一封信給他的同事Prestet（1648—1691），他在信中寫道：如何把-1/1和1/-1在比例的法則下協調起來？一方面，如果考慮分數方程-1/1=1/-1，比例法則是正確無誤的；但是另一方面，這個方程并沒有看上去那么的準確，較小的數與較大的數的比怎么可以等于較大的數與較小的數比呢？”Arcavi[33]通過讓學生在課堂中討論這一例子，在教師的引導下，讓學生在討論中澄清對負數的錯誤觀念，讓學生避免數學家的類似錯誤．教師可以通過在課堂中介紹負數的歷史，讓學生加深對負數概念的理解，澄清學生的困惑，避免錯誤的觀念重現．

2.2 從歷史錯誤中厘清相關數學知識的正確表達方式

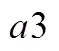
表1 整式符號的發展歷史

2.3 從歷史事件中明晰抽樣調查的樣本特征

在“6.2普查與抽樣調查”的教學中，為了預防學生在抽樣調查中出現忽視樣本的代表性和廣泛性，片面關注大樣本的錯誤情況，教師在課堂中引入“《文學文摘》雜志社對1936年總統選舉的預測”的反面故事[40]，同時引入“蓋洛普（Gallup George Horace）民意測驗所對1936年總統選舉的預測”的正面故事[41]．教師通過正反兩方面的數學史故事，引導學生避免在抽樣調查中重蹈《文學文摘》雜志社的錯誤，讓學生體會抽樣調查的樣本應該具有代表性和廣泛性的特點．

在“《文學文摘》雜志社對1936年總統選舉的預測”的反面故事中，教師通過這個故事讓學生意識到，雖然《文學文摘》采用了1?000萬的大樣本，但由于樣本缺乏廣泛性和代表性，《文學文摘》的預測最終失敗了．教師在融入反面故事的同時，引入“蓋洛普民意測驗所對1936年總統選舉的預測”的正面故事：蓋洛普在抽樣調查時，只抽樣調查了1?000個樣本，但是他注意到樣本在性別、年齡、職業、收入、種族和文化層次等基本指標的分布同美國人口的結構保持一致．這樣的樣本實際上是美國總人口的一個縮影，因而具有代表性和廣泛性．因此蓋洛普大膽預言羅斯福將連任總統，蓋洛普民意測驗的預測最終獲得成功．教師通過在課堂中介紹《文學文摘》和蓋洛普的統計學故事，使得學生對于抽樣調查的樣本選取更加的重視和認真，對于“抽樣調查要注意樣本的廣泛性和代表性”這一知識點理解的更加深入．同時，教師可以提醒學生避免重犯《文學文摘》在抽樣調查中的錯誤，澄清學生腦海中“大樣本一定能保證調查結論準確”的錯誤觀念．

3 數學史故事導入法為學生打開另一扇數學之窗

F·克萊因[42]（F. Klein）指出：“教學應遵循人類從知識的原始狀態到更高級形式的道路．推廣這種自然的、真正科學的教學的主要障礙是缺乏歷史知識．”數學史知識可以為學生的數學學習提供有力的支撐，有助于學生感受數學、感受數學文化[43]．數學家的軼聞趣事，可以激發學生學習數學的興趣[43]．數學教育需要更多的數學文化素材和數學故事來改善數學課堂的現狀．因此，整理出數個可用于初一數學課堂的數學歷史故事，為初中數學教師提供數學史融入課堂教學的素材，希望為課堂帶來一些新鮮的氣息，從而達到導入新課內容，提高學生的數學學習興趣的目的．

3.1 “科學記數法”的教學導入

在“2.10科學記數法”的新課教學中，如果一開始直接講授科學記數法的概念，會顯得有點生硬和突兀，這時不妨用一則數學史小故事作為新課的開頭，為數學課堂增添人文的色彩．這則故事的名字叫“海邊奇思”[44]．教師通過“海邊奇思”這則故事來吸引學生的注意，讓學生感到數學課的趣味．故事[45]如下：

公元前3世紀后半葉的某一天，阿基米德的朋友、敘拉古王子蓋羅在海邊散步．阿基米德三句話不離本行，談起了數學問題．

“我們腳下的這片沙灘共有幾粒沙？”阿基米德問朋友．

“想必有無窮多粒吧．”蓋羅回答．

“那整個西西里島上的沙粒數呢？”阿基米德接著問.

“當然也是無窮．”蓋羅不假思索．

“可是，親愛的朋友，不僅是西西里島，世界上任何一個地方的沙粒數都是有限的．我可以證明，我能找到一個大數，使得裝滿整個地球、甚至整個宇宙的沙粒數不超過這個數！”阿基米德自信地說．阿基米德通過他的幾何證明，證明出整個宇宙的沙粒數目不超過1后面63個0．

通過讓學生們幫助阿基米德表示出這個大數，從而引出科學計數法這一新課內容．雖然這個“海邊奇思”的故事是后人根據阿基米德的《數沙者》編寫的故事，真實性有待考究，但是從數學文化的角度來說，如果可以讓學生感受到數學之美和數學的魅力，這樣的數學文化素材也是非常具有教育意義和價值的．因此教師在課堂教學中，可以融入一些數學家的軼事、趣聞和故事，發展學生的數學意識，培養學生對數學的積極態度．

3.2 “字母表示數”的教學導入

在“3.1字母表示數”的新課講授中，教師可以運用數學故事來引起學生的有意注意，提高學生興趣．教師通過數學故事“到底有多少家伙”來回答“為什么需要用字母表示數”的問題，激發學生學習動機．在新課的教學中，教師引用英國幽默作家杰羅姆在《懶人閑思錄》[45]中的一段故事：

十二世紀的青年墮入情網，你可別指望他會后退三步，凝視情人的眼睛，然后告訴她：你太美了，美得簡直不像活人．他會說他要到外邊去看看，倘若正好碰上那么一位仁兄，并打破他的腦袋——我指的是另外那個家伙的腦袋，這就說明他——前一個人——的情人是個漂亮姑娘．但要是另一個家伙打破他的頭——不是他自己的，這你知道，而是另一個家伙的——另一個家伙是對第二個家伙而言，這就是說，因為事實上另一個家伙僅僅對于他來說才是另一個家伙，而不是第一個家伙——好了，如果他的頭被打破，那么他的女孩——不是另一個家伙的，而這個家伙……

如果一開始讓學生去看這段話，學生會感到非常的迷惑，因為學生搞不清楚到底哪個家伙是哪個家伙．如果把這段話用整式表示的話：

你瞧，如果A打破了B的頭，那么A的情人就是一個漂亮女孩；反之，如果B打破了A的頭，則A的情人不是漂亮女孩，B的情人才是[44]．

雖然這段話不是數學史，但是作為一個情景引入的數學文化素材，同樣可以讓學生感受到數學的魅力和數學文化的魅力．為了讓數學課堂充滿人文的氣息，教師可以運用一些與數學文化有關的文學素材，讓數學看上去不是那么的枯燥、抽象與生硬[33]，改善學生的數學觀[33]，展示數學教育的人文價值與人文關懷．通過杰羅姆在《懶人閑思錄》中與“字母表示數”有關的文字片段的引入，學生一定對學習“字母表示數”非常感興趣，而且覺得數學非常有用和有價值．

3.3 “綜合與實踐——幻方”的教學導入

在“綜合與實踐——幻方”課堂中，教師可以融入與“幻方”有關的數學文化和文學素材，來培養學生積極的態度．幻方是科學的結晶與吉祥的象征，發源于中國古代的洛書——九宮圖．《易經系辭》[46]記載了：“河出圖，洛出書，圣人則之．”《論語》[47]記載了：“子曰：‘鳳鳥不至，河不出圖，吾已矣夫！’”《莊子·天運》[48]提出：“天有六極五常，帝王順之則治，逆之則兇．九洛之事，治成德備，監照下土，天下戴之，此謂上皇．”《大戴禮·明堂篇》[49]中有“二、九、四、七、五、三、六、一、八”的洛書九宮數記載．教師可以通過融入幻方的歷史引入新課，讓學生了解幻方的歷史起源和發展．同時，教師還可運用金庸《射雕英雄傳》[24]中的一段“瑛姑與黃蓉的對話”作為教學素材，增添教學中的數學文化韻味，體現數學與人文之間的聯系，展示數學教育的人文價值．“瑛姑與黃蓉的對話”文摘如下：

那女子（瑛姑）沮喪失色，身子搖了幾搖，突然一跤跌在細沙之中，雙手捧頭，苦苦思索，過了一會，忽然抬起頭來，臉有喜色，道：“你（黃蓉）的算法自然精我百倍，可是我問你：將一至九這九個數字排成三列，不論縱橫斜角，每三字相加都是十五，如何排法？”

黃蓉心想：“我爹爹經營桃花島，五行生克之變，何等精奧？這九宮之法是桃花島陣圖的根基，豈有不知之理？”當下低聲誦道：“九宮之義，法以靈龜，二四為肩，六八為足，左三右七，戴九履一，五居中央．”邊說邊畫，在沙上畫了一個九宮之圖．

那女子面如死灰，嘆道：“只道這是我獨創的秘法，原來早有歌訣傳世．”

黃蓉笑道：“不但九宮，即使四四圖，五五圖，以至百子圖，亦不足為奇．就說四四圖罷，以十六字依次作四行排列，先以四角對換，一換十六，四換十三，后以內四角對換，六換十一、七換十．這般橫直上下斜角相加，皆是三十四．”那女子依法而畫，果然絲毫不錯．

黃蓉道：“那九宮每宮又可化為一個八卦，八九七十二數，以從一至七十二之數，環繞九宮成圈，每圈八字，交界之處又有四圈，一共一十三圈，每圈數字相加，均為二百九十二．這洛書之圖變化神妙如此，諒你也不知曉．”

黃蓉對幻方的深入研究，使得自以為是“神算子”的瑛姑自嘆不如，連聲感嘆“罷了，罷了！”當學生讀到這一小說片段，會對幻方產生濃厚興趣，產生積極學習的心向，從而教師可以順利地開展新課．除了文字資料的呈現以外，教師還可以提供視頻資料，將電視劇中《射雕英雄傳》關于“幻方”的片段在課堂中播放出來，讓學生對“幻方”留下深刻印象，產生濃厚興趣，同時引出幻方的新課內容．數學文化包含動態的數學過程，其中存在著豐富的數學精神、理念和價值觀[50]．如果數學教師只注重數學知識的學習，而忽視數學文化的熏陶，并不是完整的數學教育，學生在這樣的學習環境里難以獲得充分的培育和發展[50]．

4 結語

數學課堂有效滲透數學史能夠使學生了解數學的來龍去脈，激發并保持學生的數學學習興趣，從而提高數學學習的長久效益．但必須注意的是，如果課堂教學只是把數學史從古代到現代匆匆走一回，羅列期間在科學上發生的主要事件和日期，那么它的教育價值與只要求學生熟記歷代皇朝的年份沒有任何區別．在講課中，完全沒加入數學史比胡亂加入數學史的課堂效果會更好．弗賴登塔爾[51]強調：“我們不應該完全遵循發明者的歷史足跡，而應是遵循經過改良、同時有更好引導作用的歷史過程．”教師在教學中不應簡單地去重復當年的真實歷史，而應致力于數學歷史的重構，發揮重要的指導作用，更加注重學生的主動發現，將數學課真正“教活、教懂、教深”[52]．為了實現弗賴登塔爾所倡導的“數學再創造”，將數學的歷史和文化融入數學課堂必須謹慎執行，教師在實踐的過程中應該保持專業性和高效性．

研究將所提及的教學案例的相關知識點、教學章節、數學史素材、教學方式、教學方法、數學史融入的方法和教學環節進行了整理，希望對一線數學教師實施數學史融入數學課堂的教學方法提供有益的幫助（如表2所示）．

表2 數學史融入課堂的運用方式

數學課堂的教學改革需要教育取向的數學史與數學文化研究，開發與中學教學內容相契合的數學史融入數學課堂案例，培養學生對數學的積極態度[53]．在數學課堂上融入數學史和數學文化，不僅僅為了調節課堂氣氛，發揮調味品的作用，更重要的是讓學生理解數學的歷史和現狀，培養學生對數學的積極態度．教師通過數學史融入課堂，轉變學生對于數學刻板、枯燥和抽象的看法，改善學生的數學觀．這不是一項容易的事情，新時代的數學老師需要學習數學史，了解數學知識的來龍去脈[54]，從而更好地肩負起這項責任．研究提供了數學史融入數學課堂的運用方法，以及數學史融入數學課堂的案例，旨在為初中數學教師能更高效、更專業地開展數學史融入數學課堂的實踐提供可資借鑒的數據和實例．

[1] WILKINS M. Preparing for the 21st century: the status of quantitative literacy in the United States [J]. School Science & Mathematics, 2010, 100 (8): 405-418.

[2] JONES P S. The history of mathematics as a teaching tool [J]. Mathematics Teacher, 1957, 50 (1): 59-64.

[3] MCBRIDE C, ROLLINS H. The effects of history of mathematics on attitudes toward mathematics of college algebra students [J]. Journal for Research in Mathematics Education, 1977, 8 (1): 57-61.

[4] FAUVEL J. Using history in mathematics education [J]. For the Learning of Mathematics, 1991, 11 (2): 3-6.

[5] LIU P H. Do teachers need to incorporate the history of mathematics in their teaching [J]. Mathematics Teacher, 2003, 96 (6): 416-421.

[6] NG W L. Effects of an ancient Chinese mathematics enrichment program on secondary school students’ achievement in mathematics [J]. International Journal of Science & Mathematics Education, 2010, 8 (1): 25-50.

[7] SCHIEFELE U, KRAPP A, WINTELER A. Interest as a predictor of academic achievement: a meta-analysis of research [M] // RENNINGER A, HIDI S, KRAPP A. The role of interest in learning and development. Hillsdale: Lawrence Erlbaum, 1992: 183-212.

[8] KATZ V J. Using history in teaching mathematics [J]. For the Learning of Mathematics, 1986, 6 (3): 13-19.

[9] 汪曉勤，歐陽躍．HPM的歷史淵源[J]．數學教育學報，2003，12（3）：24-27．

[10] JANKVIS T. A categorization of the “whys” and “hows” of using history in mathematics education [J]. Educational Studies in Mathematics, 2009, 71 (3): 235-261.

[11] 汪曉勤．HPM的若干研究與展望[J]．中學數學月刊，2012（2）：1-5．

[12] TZANAKIS C, ARCAVI A, SA C, et al. Integrating history of mathematics in the classroom: an analytic survey [M] // FAUVEL J, MAANEN V J. History in mathematics education. Netherlands: Springer, 2002: 201-240.

[13] 馬復．義務教育教科書：七年級上冊數學[M]．北京：北京師范大學出版社，2017：1-200．

[14] 蕭文強．心中有數：蕭文強談數學的傳承[M]．大連：大連理工大學出版社，2010：50-54．

[15] 劉徽．九章算術注[M]．南京：江蘇科學技術出版社，2016：20-23．

[16] 林夏水．畢達哥拉斯學派的數本說[J]．自然辯證法研究，1989（6）：48-58．

[17] ALEXANDERSON G. About the cover: Christopher Clavius, astronomer and mathematician [J]. Bulletin of the American Mathematical Society, 2009, 46 (4): 669-670.

[18] SMITH D E. History of mathematics [M]. New York: Dover Publications, 1953: 15-17.

[19] 歐幾里得．幾何原本[M]．利瑪竇譯，徐光啟述．上海：上海古籍出版社，2011：60-62．

[20] 朱世杰．新編算學啟蒙[M]．羅士琳附釋．上海：上海古籍出版社，1996：23-24．

[21] 吳文俊．中國數學史大系：第6卷西夏金元明[M]．北京：北京師范大學出版社，1999：57-59．

[22] ROSEN F. The algebra of Mohammed Ben Musa [M]. Whitefish: Kessinger Publishing, 2010: 91-92.

[23] 棣么甘．代數學（卷三）[M]．李善蘭，偉烈亞力，譯．上海：墨海書館，1859：74-76．

[24] 金庸．射雕英雄傳[M]．廣州：廣州出版社，2008：145-146．

[25] 曾崢．略論數學的人文價值[J]．數學通報，2002，41（2）：12-15．

[26] 曾崢，邢惠清．開發數學課程的文化教育功能[J]．學科教育，2000（12）：20-23．

[27] 斯賓塞．斯賓塞教育論著選[M]．北京：人民教育出版社，2005：206．

[28] 弗賴登塔爾．數學教育再探：在中國的講學[M]．上海：上海教育出版社，1999：137．

[29] ?FREUDENTHAL H. Should a mathematics teacher know something about the history of mathematics [J]. For the Learning of Mathematics, 1981, 2 (1): 30-33.

[30] ?PóLYA G. Mathematical discovery. On understanding, learning and teaching problem solving (Vol. II) [M]. New Jersey: John Wiley & Sons, 1965: 51.

[31] ?FLORIAN C. A history of elementary mathematics; with hints on methods of teaching [M]. New York: The Macmillan Company, 1924: 47.

[32] 佟巍，汪曉勤．負數的歷史與“負負得正”的引入[J]．中學數學教學參考：教師版，2005（1）：126-128．

[33]?ARCAVI A. The experience of history in mathematics education [J]. For the Learning of Mathematics, 1991, 11 (2)：7-16.

[34]?PAUL S. Arnauld, malebranche, prestet et la theorie des nombres negatifs (d'après une correspondance retrouvée) [J]. Thalès, 1935, 2 (1): 82-90.

[35] ?FRAN?OIS V. The analytic art [M]. New York: Dover Publications, 2006: 12-13.

[36]?HARIOT T. Artis analyticae praxis ad aequationes algebraicas resolvendas [M]. Chester: Readex Microprint, 1970: 36-37.

[37] ?ROSA M E. Symbolic language in early modern mathematics: the algebra of Pierre Hérigone (1580—1643) [J]. Historia Mathematica, 2008, 35 (4): 285-301.

[38] ?DESCARTES R. The geometry of Rene Descartes [M]. Whitefish: Kessinger Publishing, LLC. 2008: 39-40.

[39] ?EULER L. Introductio in analysin infinitoruin [M].Whitefish: Kessinger Publishing, LLC. 2010: 52-53.

[40] ?LOHR L, MICHAEL J, MIDDLETON A. Roosevelt predicted to win: revisiting the 1936 literary digest poll [J]. Statistics Politics & Policy, 2017 (8): 65-84.

[41] ?WOOD P. George H. Gallup [J].The journal of marketing. 1962, 26 (4): 78-80.

[42] 菲利克斯?克萊因．高觀點下的初等數學[M]．上海：復旦大學出版社，2008：222．

[43] 朱哲，宋乃慶．數學史融入數學課程[J]．數學教育學報，2008，17（4）：11-14．

[44] 田方琳，汪曉勤．初中數學課堂上的數學故事[J]．中學數學月刊．2013（9）：50-53．

[45] 杰羅姆．懶人閑思錄[M]．北京：外語教學與研究出版社，2009：117．

[46] 王易中．大智之門：孔子《易?系辭》解讀[M]．太原：山西科學技術出版社，2011：149．

[47] 楊伯峻．論語譯注：簡體字本[M]．北京：中華書局，2006：69．

[48] 莊周．莊子[M]．太原：山西古籍出版社，2003：42．

[49] 戴德輯．大戴禮記[M]．濟南：山東友誼出版社，1991：74．

[50] 謝明初．數學教育的人文追求[J]．數學教育學報．2015，24（1）：6-8．

[51] FREUDENTHAL H. Didactical phenomenology of mathematical structures [M]. Dordrecht: Kluwer Academic Publishers, 2002: 23.

[52] 鄭瑋，鄭毓信．HPM與數學教學中的“再創造”[J]．數學教育學報．2013，22（3）：5-7．

[53] 趙東霞，汪曉勤．關于數學文化教育價值與運用現狀的網上調查[J]．中學數學月刊，2013（3）：41-44．

[54] ?KATZ V J. A history of mathematics [M]. New York: Higher Education Press, 2008: 2.

A Case Study of Integrating Mathematical History into Junior High School Classrooms

ZENG Zheng1, YANG Yu-hui1, LI Xue-liang2

(1. Foshan University, Guangdong Foshan 528000, China; 2. Foshan Nanhai District Nanhai Experimental Middle School, Guangdong Foshan 528000, China)

The current junior high school mathematics classroom placed too much emphasis on the students’ ability to master the knowledge of mathematics content and develop students’ mathematics reasoning ability. However, they neglected to allow students to understand the current situation and historical development of mathematics and cultivate students’ positive attitude towards mathematics. The integration of mathematics history into junior high school mathematics classroom teaching allowed students to understand the current state and history of mathematics and to develop students’ positive attitude towards mathematics. This article provided methods for Integrating the history of mathematics into the mathematics classroom for junior high school students, and conducted case studies on the integration of mathematics history into the junior high school class to provide teaching references for junior middle school mathematics teachers. The case study of the integration of mathematics history into the junior high school classroom was mainly divided into three parts: 1. deepening the understanding of mathematical concepts; 2. avoiding mathematicians from making mistakes; 3. introducing new classes to improve interest in learning.

history of mathematics; junior high school mathematics teaching; teaching method; case study

2018–08–08

佛山市教育局教育科學規劃2017年度專項課題——初中數學教師課程資源開發：現狀、問題及對策（FSGH201711）

曾崢（1962—），男，廣東蕉嶺人，教授，碩士研究生導師，主要從事數學史、數學文化和數學教育的研究．

G633.6

A

1004–9894（2019）01–0012–07

曾崢，楊豫暉，李學良．數學史融入初中課堂的案例研究[J]．數學教育學報，2019，28（1）：12-18．

[責任編校：張楠、陳雋]