混凝土壩長期運行安全的理想點法評價模型

劉 晗,李明超,沈 揚,張 野

(天津大學水利工程仿真與安全國家重點實驗室,天津 300354)

根據水利部2016年發布的統計報告[1],全國已建成各類水庫97 988座,其中大型水庫707座,中型水庫3 844座。這些水庫大多修建在20世紀50—70年代,由于當時可能存在設計標準偏低、施工質量較差的情況,在大壩建成時就存在諸多隱患;隨著大壩運行年限的增加,一些大壩出現了老化病態問題,大壩失事事件也偶有發生。大壩長期運行的安全狀況不僅關系到整個工程的安危,而且對經濟建設、社會安定與生態安全等具有重大影響,大壩工程的安全問題受到廣泛關注[2]。大壩安全評價是對大壩運行狀態及大壩安全程度的整體性評價,它以大壩的各項監測數據為基礎,通過利用現代數學和計算機技術挖掘數據中存在的特征來反映大壩的長期運行狀態,是保障大壩安全的重要手段。近年來,隨著數字大壩的發展,大壩安全評價數據獲取更加方便且全面,評價的方法也變得多元,國內外很多學者都對大壩安全的評價方法進行了研究探討,灰色關聯度理論、模糊綜合評價方法[3]、數據融合理論[4]、信息熵理論[5]、層次分析法[6]及神經網絡[7]等相繼被引入到大壩安全評價領域中,對大壩安全評價的研究起到了重要的推動作用。

目前對混凝土壩安全評價方法的研究取得了很多成果,如,李春雷等[8]將層次分析法和模糊數學理論相結合,建立了大壩安全的多層次模糊綜合評價模型,利用該模型能夠對大壩實際安全情況進行量化分析;宋恩來[9]將三維非線性有限元方法應用到混凝土壩整體安全度評價中,并應用到豐滿水電站,通過超載安全系數對比證實了可行性;李同春等[10]提出了基于有限元分析結果的高拱壩安全度評價體系,研究了壩體裂縫對大壩工作性態的影響,給出了壩體容許裂縫長度;蘇懷智等[11]建立了基于二次拋物線形抗剪強度包絡線的功能函數,并結合改進的當量正態化法,提出了高壩壩基失穩可靠度的計算方法,計算求出高壩壩基的穩定可靠度,達到了合理評估高壩壩基穩定性的目的;王少偉等[12]將尖點突變理論引入拱壩-地基的安全度評價中,建立了相應的模型,評判結果與塑性屈服區貫通準則一致;何勇軍[13]應用模糊集理論對大壩的安全狀態進行判斷,建立了大壩安全綜合評價模型,應用實例表明該模型是可行的;高健等[14]將模糊數學應用到拱壩的安全評判,建立了考慮厚高比、柔度和最大拉應力3個因素的模糊綜合評價模型,實例驗證結果表明,評判結果切合實際;Feng等[15]提出了評估壩頂裂縫和高拱壩極限承載能力的一系列安全因素,并對高拱壩進行了較為合理的評估;劉愚[16]提出基于熵權-理想點法的大壩安全評價模型,制定了相應的評價標準及安全等級,通過某具體工程證明了模型的可行性;李影等[17]引入理想點法確定大壩評價的標準和評價等級,通過組合賦權的方法確定各指標權重。上述研究在大壩安全評價方面取得了重要的進展和成果,由于實際工程中混凝土壩結構的特殊性、地質條件的復雜性及外部環境的易變性,導致混凝土壩的安全度隨時間動態變化,有必要根據實際監測數據對混凝土壩長期運行過程的安全度進行綜合評價分析。本文通過分析影響混凝土壩安全的因素,構建混凝土壩安全評價指標體系,建立基于理想點法的混凝土壩安全評價模型,并通過工程實例驗證模型的合理性。

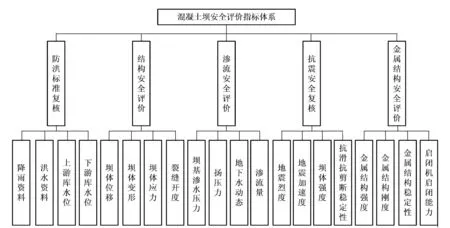
圖1 混凝土壩安全評價指標體系

1 混凝土壩長期運行安全評價指標體系

1.1 混凝土壩安全因素分析

混凝土壩是一個非常復雜的系統,影響混凝土壩安全的因素來自各個方面,涉及地質條件、水文條件、壩體構造、壩體強度、施工質量、水庫運行管理方式、環境因素和人類活動等[18]。根據文獻[19]統計的74座混凝土壩的潰壩模式,其中31.1%是由漫頂破壞導致的,原因可能是遭遇大洪水、溢洪道泄流能力不足、兩岸滑坡等;36.5%是由壩基或壩肩破壞導致的,原因主要有兩點,一是壩基存在軟弱夾層或斷層等地質缺陷,二是大壩防滲體系或排水設備缺陷;9.5%是由壩體結構破壞導致的,主要原因是壩體材料質量惡化、材料強度降低;9.4%是由地震、人為破壞或設計運行維護不當等導致的;另外還有13.5%的混凝土壩潰壩模式原因不詳。

基于以上分析,從混凝土壩的外荷載與壩自身的效應兩方面綜合考慮,建立混凝土壩安全評價指標體系,對混凝土壩的安全度進行計算評價,以便對大壩存在的缺陷或破壞及時發現和制止。

1.2 安全評價指標體系建立

混凝土壩安全評價體系主要包括安全評價指標和評價指標的分級標準,由于混凝土壩在多因素的作用下性能退化機理極為復雜[20],綜合考慮大壩會受到顯著的水位及環境溫度變化的影響[21]、混凝土壩長期變形的影響[22]等,這里選取評價指標時綜合考慮了大壩結構、環境因素及監測系統的影響[23],建立混凝土壩安全綜合評價指標體系如圖1所示。

從圖1可以看出,指標評價體系包含了防洪標準復核、結構安全評價、滲流安全評價、抗震安全復核及金屬結構安全評價五方面共20個具體的評價指標,能夠較好地反映混凝土壩長期安全運行的綜合狀況。同時,考慮到混凝土壩長期安全性問題受控于材料及結構性能的劣化,即混凝土壩的材料及結構性能隨著時間的推移逐漸變差,在評價過程中通過對監測數據的長期評價間接反映“時效性”這一指標,由于時效數據不能通過儀器檢測直接得到,這里并未將其列入該指標體系。

2 基于理想點法的混凝土壩安全評價模型

理想點法是求解多目標規劃問題的一種評價函數方法,其原理是使目標值盡可能地逼近理想值。采用理想點法進行混凝土壩安全評價分析[24-25],是在確定合理的評價指標體系基礎上,先通過層次分析法(analytic hierarchy process,AHP)和獨立信息波動賦權法(weight giving based on data independence and data fluctuation,DIDF)計算各指標權重,然后定義一種“距離”,即在多維歐式空間中的一個點,在這種“距離”的意義下,找到一個盡可能接近理想點的點,使該點與正理想點評價函數距離最小,與負理想點評價函數距離最大,通過理想點貼近度對混凝土壩安全度進行計算分類,最終給出定量的評價結果。

2.1 混凝土壩安全評價指標矩陣構造

2.1.1 構造初始矩陣

根據混凝土壩的屬性和結構特點確定合理的評價指標體系,并根據混凝土壩的各個指標建立相應的矩陣。設待評價的對象為m個,評價指標為n個,第i個評價對象的第j個評價指標數據表示為xij,形成初始矩陣:

(1)

2.1.2 原始數據標準化

數據的標準化處理包括評價指標的同趨勢化、非量綱化和原始數據歸一化。同趨勢化使規范后的任一指標屬性越優的指標值越大,非量綱化可以排除量綱的選用對評價的影響,原始數據歸一化即把數值均變化到[0,1]區間里,具有數據尺度統一、方便后面的數據處理、簡化計算等優點。

a. 對混凝土壩的位移、應變及裂縫開度指標進行先求絕對值再歸一化:

(2)

式中:yij為xij的歸一化值;xjmax為所有評價對象里第j個評價指標數據的最大值;xjmin為所有評價對象里第j個評價指標數據的最小值。

(3)

可得到初始的標準化矩陣Y=(yij),將Y矩陣進行矩陣歸一化處理:

(4)

得到標準化矩陣:

(5)

2.1.3 評價指標權重計算

權重是表征指標重要性的權值,表明指標在整體評價中的重要程度。一般確定指標體系權重的方法分為主觀賦權法和客觀賦權法。主觀賦權法即根據以往的工程經驗、特殊的地理條件、氣候條件以及混凝土壩的結構特性綜合考慮得出混凝土壩的各個評價指標的權值。客觀賦權法即基于各個指標的監測數據通過某些特定的算法計算權重。主觀賦權法簡單,主要依靠評判人員的經驗,人為因素太強;客觀賦權法又過于依賴實時監測數據,這兩種方法都存在一定的信息量的損失。為了全面地反映評價指標的重要性,使得評價結果更加準確,采用主觀賦權與客觀賦權相結合的組合賦權方法,最大限度地減小信息量的損失,使所獲得的權重更接近各指標的實際情況。

a. 確定主觀權重。選用AHP法來求取各指標的主觀權重。AHP法使用簡便,系統性強,所需數據信息少,是一種常用的主觀權重選取方法。AHP法確定權重的具體步驟可參見文獻[26]。

b. 確定客觀權重。選取DIDF法確定客觀權重[27]。DIDF法將數據自身信息與信息獨立程度進行了組合,有效解決了熵權法、離散系數法等只考慮數據波動信息而未考慮信息間獨立程度的問題,能夠更真實地反映不同指標間的重要程度。

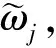
(6)

式中:wj為第j個評價指標的組合權重;λ為主客觀權重的分配系數。

2.1.4 加權評價指標矩陣確定

由組合賦權法確定的組合權重為

w=(w1,w2,…,wn)

(7)

根據標準化后的矩陣V和組合權重向量,則可構建最終評價指標矩陣為

(8)

2.2 正負理想點確定

在評價指標體系中,評價指標一般劃分為效益型指標和成本型指標兩大類,效益型指標表示指標值越大則評價結果越優,成本型指標表示指標值越小則評價結果越優。由于本文的數據標準化處理過程將所有指標處理成了效益型指標,則正、負理想點可以定義如下:

(9)

2.3 理想點評價函數

(10)

(11)

理想點相對接近度Ci,即混凝土壩的評價對象i的安全度值，可表示為

(12)

Ci值的區間為[0,1],Ci值越大,則到正理想點距離越小,到負理想點距離越大,混凝土壩安全度越高。

3 實例驗證

某水利樞紐主要建筑物包括船閘、電站廠房、泄水閘、沖沙閘及擋水建筑物。壩型為混凝土壩,最大壩高47 m,壩面長度2 606.5 m,壩軸線長2 595.1 m。設計水位高程66 m,總庫容15.8億 m3。壩基巖石由砂巖、粉砂巖、礫巖組成,壩體工程量為580萬m3,1988年12月竣工。為了檢測大壩的運行狀態,在施工的各個階段同時埋設和安裝了很多檢測儀器,如鋼筋計、應變計、溫度計和測縫計等。

3.1 混凝土壩安全評價指標選取

根據監測儀器布置及監測項目,重點在沖沙閘壩段壩基部位(圖2,其中藍色點表示應變計、紅色點表示鋼筋計、綠色點表示測縫計)建立混凝土壩結構安全評價指標體系,再對影響混凝土壩的環境因素建立安全評價指標體系,對混凝土壩的結構因素與環境因素進行相互驗證,并且對多個典型控制點分別進行評價,能夠有效解決單個測點評價的偶然性與局部最優性問題。

圖2 沖沙閘壩段儀器布置三維模型

大壩結構安全選取了沖沙閘壩段壩基部位高程為36.6 m處壩基的應變、沖沙閘閘孔頂部及側面的2個典型測點的應力、測縫計測得的壩基變形和壩面位移5個指標。由于影響大壩的荷載主要是氣溫、庫水位和時效,因此選取溫度與水位作為環境指標,并進行持續性分析。考慮到氣溫、庫水位對混凝土壩影響的滯后性,因此將上月庫水位、上月氣溫加入到評價指標體系,構建了氣溫、庫水位、上月氣溫、上月庫水位4個因素的環境評價指標體系。

3.2 組合權重確定

組合權重是主觀權重與客觀權重根據線性加權組合計算得來的,主觀權重計算采用AHP法,客觀權重計算采用DIDF法。

根據下式計算層次分析矩陣的隨機一致性比率CR:

(13)

式中:CI為一致性指標;RI為平均隨機一致性指標;λmax為最大特征值。

查平均隨機一致性指標RI標準值表得當n=5時,RI=1.12,由式(13)求得CR=0.002<0.1,所以一致性較好,求得的權重可以作為結構安全評價指標的主觀權重。

用DIDF法分別計算環境指標與結構安全指標的客觀權重。經計算得出結構安全評價指標的客觀權重向量ωx=(0.133,0.254,0.088,0.331,0.194);同理可求得環境評價指標的客觀權重向量ωh=(0.202,0.298,0.202,0.298)。

將AHP求得的主觀權重與DIDF法求得的客觀權重代入式(6),分配系數取0.5,求出結構安全評價指標與環境評價指標的組合權重如表1和表2所示。從表1可以看出,結構安全評價指標對大壩安全度的影響由大到小依次為壩基變形、壩面位移、孔頂應力、壩基應變、孔側應力。從表2可以看出,環境評價指標對大壩安全度的影響由大到小依次為上月庫水位、庫水位、上月氣溫、氣溫。

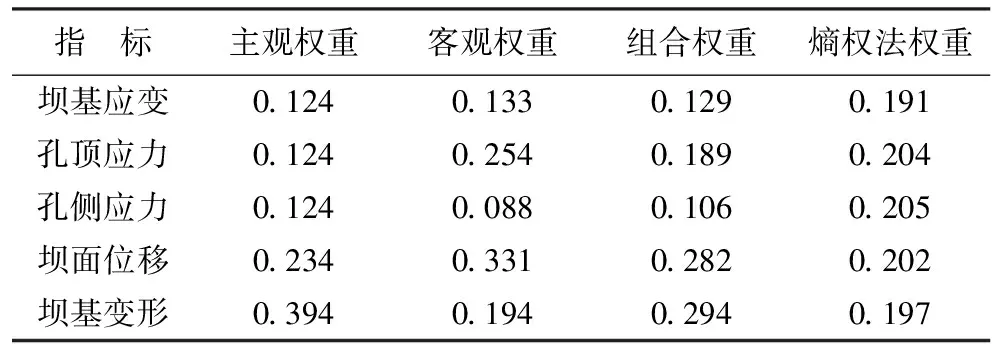
表1 結構安全評價指標權重

表2 環境評價指標權重

為了進一步驗證本文建立模型的合理性,采用文獻[16]的熵權理想點法對監測數據進行了計算,求得各評價指標的權重結果一并列于表1和表2中,可以看出使用文獻[16]中的方法求得的結構安全指標權重與環境指標權重都出現了平均化的趨勢,與工程實際不相符,原因是熵權法只考慮了數據的波動性,并未考慮各監測指標間的獨立程度,本文采用的DIDF法則綜合考慮了以上兩點,且在此基礎上耦合AHP法,有效解決了客觀賦權法過于依賴監測數據的局限性。

3.3 混凝土壩安全度評價分析

基于理想點法對混凝土壩多個測點長期運行監測數據進行了計算,通過式(8)～(10)計算得到了混凝土壩結構安全指標體系的實時安全度值,圖3為兩個典型控制點的結構安全指標安全度。對影響混凝土壩的環境因素進行了實時的安全評價,得出了混凝土壩環境指標的實時安全度如圖4所示。

圖3 混凝土壩結構安全指標安全度

圖4 混凝土壩環境指標安全度

從圖3可以看出,兩個控制點有著相同的變化規律，其安全度均出現了明顯的以年為周期的變化,控制點A的安全度波動幅度略大于控制點B。安全度在每年的8、9月出現最低值,這是由于結構安全評價指標主要是壩基內的應力、應變、變形與壩面位移,在8、9月氣溫高,混凝土受熱膨脹導致溫度應力大,會出現安全度偏低的情況,符合工程實際。

從圖4可以看出,環境指標也出現了周期性變化趨勢,安全度最低值分布在每年的1、2月。由于環境指標主要是氣溫與庫水位,在每年冬天低溫產生的凍脹效應會對壩體產生不利的影響,所以會呈現出1、2月安全度值偏低的情況,環境指標的安全度在7、8月也呈現出較低的情況,這是由于夏季氣溫高,混凝土溫度應力提高,并且壩址所在地夏季多雨,庫水位上漲,評價結果與實際情況相符。

綜合以上模型求得的各評價指標權重值與混凝土壩安全度值,本文模型計算結果與工程實際安全狀態相符,計算簡便,能夠較好滿足工程安全評價的需要。

4 結 語

本文將理想點法應用于混凝土壩長期運行安全評價中,通過分析混凝土壩的安全因素構建了混凝土壩安全評價指標體系,評價指標綜合考慮了影響混凝土壩安全的內、外因素,能夠較充分地反映混凝土壩結構運行的安全狀態。利用AHP法與DIDF法綜合確定各指標的權值,建立了混凝土壩長期運行安全的理想點模型,將模型應用于某實際混凝土壩工程安全度評價,環境指標與結構安全指標評價結果互相吻合,并且與工程實際運行狀態相符,表明該評價模型能夠客觀反映混凝土壩的安全度。