基于節點內聯性的傳播網絡推斷模型研究

徐楠楠,胡晨光,于曉輝

?

基于節點內聯性的傳播網絡推斷模型研究

徐楠楠1,胡晨光1,于曉輝2

1. 北京電子科技職業學院 信息中心, 北京 100176 2. 北京物資學院 物流學院, 北京 101149

為了有效克服傳播網絡節點推斷時，無法準確獲得感染時間信息的問題，首先通過不同節點感染情況間信息直接量化節點間的內聯性，由此確定所有可能存在的影響關系。其次，構造出節點感染傳播概率的相關對數似然函數，通過期望最大化法進行處理，同時計算感染傳播概率。結果表明，相較當前算法而言，該算法優勢較為明顯，一方面能實現傳播網絡更準確推斷，另一方面能減少執行時間，進一步保證處理效率。

傳播網絡; 內聯性; 推斷模型

傳播路由網絡推斷主要以多次傳播過程中所有節點被感染情況為基礎，進而推斷不同節點間影響關系與感染傳播概率。各條間相互影響的關系均可被設定為一條有向邊（由一父節點至一子節點），代表這一父節點受感染后直接把感染內容（疾病、信息等）傳播到這一子節點，由此改變子節點感染情況；感染傳播概率代表受感染父節點把感染內容傳播到未感染子節點，后者能被感染的概率，該可量化的概率值表明傳播網絡內影響關系。為明確傳播路由網絡內傳播過程，必須了解上述影響關系與感染傳播概率，如此便能更準確推測后期傳播行為。比如，網絡信息安全部門能在病毒傳播網絡基礎上面向易感節點實施防控布署，輿情監控員能在輿論傳播網絡基礎上推測輿論演變勢態[1]。

從部分傳播過程來看，如在線社交媒體上輿論傳播過程，感染時間記錄、獲取比較簡單，但從現實世界大量傳播過程來看，如網絡路由傳播過程或者疾病傳播過程，通常不能準確、全面、有效獲取這部分信息[2]。這是因為現實世界很難實時監控感染情況或定期完成感染情況普查工作。除此之外，即便上述要求全部得到滿足，但在節點間感染潛伏期(從受感染直至癥狀發生所用時間)有所區別等因素影響下，觀測確定感染時間不一定代表節點準確、有效感染時間。故而對現實世界具體應用而言，當前大部分算法缺乏可用性與合理性[3,4]。

為克服當前大部分算法不足之處，本次建立了只需根據若干次傳播過程完成后觀測所得不同節點感染情況，推測網絡內不同節點間影響關系與感染傳播概率。首先，通過不同節點感染情況間互信息直接量化彼此間內在關聯。因為大部分節點感染情況間屬于弱關聯，所以很多互信息值偏小，由此產生內聚性傾向，以此為前提，可對存在強、弱關聯的節點進行準確劃分，發現可能的影響關系。其次，構造出節點感染情況觀測結果（變量是感染傳播概率）相關對數似然函數，通過期望最 大化法進行處理，同時計算出感染傳播概率。

1 問題描述

面對傳播路由網絡進行問題推斷時，通常將該網絡視作一有向圖(,)，={v,…,v}表示節點集合，擁有該網絡內部個節點；表示節點間有向邊集合，各條有向邊(v,v)指代父節點v對子節點v有影響關系，同時大多以(v,v)指代v與v間感染傳播概率。隨著(v,v)不斷增大，代表v受感染后，如果v未感染，那么v較大概率受v感染。不僅如此，各次傳播過程中，被感染節點可利用有向邊感染一些相鄰未感染節點，如果節點成功受感染，那么狀態始終固定。

本文在進行分析討論時，針對無需感染時間的傳播網絡推斷問題，重點是個節點次傳播過程完成后各節點感染狀態數據={1,…,S}已知情況下，推斷節點間影響關系，換言之，需要得出有向邊集合，與各條有向邊對應的感染傳播概率。已知情況下，S={,…,}代表第次(1≤≤)傳播過程完成后節點感染狀態集合。若=1、=0，分別表示第次傳播過程中v被感染、沒有感染。

2 本文所設計算法

下面本文首先重點描述以節點感染狀態間互信息為基礎的影響關系推斷算法，最后明確本文算法基本步驟。

2.1 節點間影響關系推斷

通常來講，對于多次傳播過程而言，假若隨機兩節點v、v感染狀態值s?{0,1}與s?{0,1}服從等式(S=s,S=s)=(S=s)(S=s)，則S與S分別指代v、v感染狀態變量，此時能夠認為v、v感染狀態彼此獨立，沒有關聯關系，換言之v、v間不可能有影響關系。從信息論來看，互信息一般用于量化評價兩變量間關聯關系。

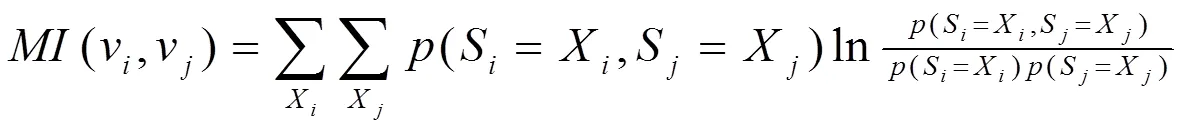
早期進行互信息計算時，需要注意兩節點所有感染狀態，也就是v與v各自兩種感染狀態值（含0與1）間關聯關系。早期算法主要基于統計學評價不同節點間關系，沒有考慮v被感染（S=1）、v被感染（S=1）事件間關聯關系。為明確節點間影響關系，需要判斷感染事件（S=1與S=1）之間有無關聯。所以，針對感染事件之間關聯程度，本文給出改進后互信息算法進行處理，詳情如下：

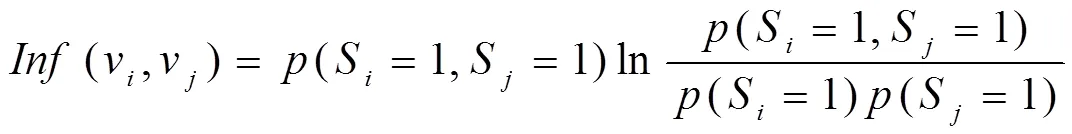
(v,v)取值較大時，表示v與v感染事件之間存在較明顯關聯關系，換言之，v與v間具有影響關系的可能性較高；相反，若(v,v)取值無限趨向為0，那么v與v間由影響關系可能性也無限趨向為0。

大部分情況下，傳播網絡內單一節點v影響區域較小，簡單來講，當節點僅能被v輕微影響時，它和v間才會出現較大改進互信息值；不難理解，大部分節點和v間改進互信息值非常低（無限趨向為0）。所以，許多較小改進互信息取值會產生相應內聚性，由此和極大改進互信息取值得到有效分類。-均值算法、支持向量機等劃分聚類算法均能得到一改進互信息閾值，借此區別較大、較小改進互信息取值。這里選擇-均值算法來說明，區別改進互信息時，可采用以下步驟實現：（1）為所有節點求出它和剩余節點間改進互信息；（2）令=2，執行-均值算法，把全部互信息取值區別成兩個聚類；（3）設定閾值，即從較大聚類中直接確定最小改進互信息值。

從值出發，可確定對節點存在潛在影響關系一些父節點集合F：

F={v|v?,v1v,(v,v)≥}集合F代表最可能讓v被感染節點，因此下面需要討論何種節點間感染傳播概率方案最大幾率形成次傳播過程完成后節點感染狀態數據。除此之外，通過聚類算法確定互信息時，容易出現噪點，也就是關于各節點v=?F可能包含非真實父節點，但推斷感染傳播概率時可有效去除。

2.2 算法步驟

本文主要將參數調整閾值Error（其將所有節點感染狀態數據與當作期望最大化算法[5]收斂條件，故綜合考慮之下，這里Error取0.0001）視作輸入數據，輸出不同節點v?相關父節點集合F與所有感染傳播概率。經歸納整理可知，算法包含4個階段，具體說明如下：（1）求出全部改進互信息；（2）通過-均值求出改進互信息相關閾值；（3）為各節點v?求其潛在父節點集合F；（4）通過期望最大化算法迭代所有感染傳播概率(v,v)，最終符合收斂條件。

3 結果與分析

這里先介紹實驗相關設置，后探討各種因素給節點間影響關系、感染傳播概率推斷結果、算法用時帶來的影響，相關因素包括傳播網絡節點數量與邊密度（邊與節點總數之比）、初始感染節點比例等。此次實驗過程中，所有算法都以Java來建立，并選擇Windows 10操作系統，3.7 GHz的Intel Core i 3-6100 CPU和8 GB內存臺式機。

3.1 實驗設置

這里人工合成傳播網絡選用LFR基準圖[6]，進而測試算法準確性和執行時間。從LFR網絡來看，可設定各種點、邊數量，由此創建各種傳播網絡(詳情如表1所示)。除此之外，本次引入微博中真實傳播網絡DUNF[5]，內含750個節點(用戶)以及2794條邊（關注與轉發量）。

表 1 LFR網絡

基于這部分人工合成與實際網絡結構，設定網絡內部邊的傳播概率滿足高斯分布（均值是0.3，方差是0.05），保證超過95%概率值處于0.2~0.4區間內。同時采用獨立級聯模型，有效模擬次爆發無時間信息情況，借此重構這部分網絡。

針對傳播網絡推斷準確性，主要通過值、均方誤差（MSE）進行評價，針對算法效率，主要以執行時間進行評價。本文選擇兩種算法當作比較方法，其一，高性能基于感染時間的算法Net Rate[7]；其二，高效且與感染時間無關的算法LIFT[8]。

3.2 傳播網絡節點數量的影響

即傳播網絡內所有支持數據傳播的節點數量，一般能夠反映傳播網絡大小。這里共選擇5個傳播網絡（LFR1-5，同一平均度而節點數目存在差異）進行分析，由此判斷這類節點數量給真實結果帶來的影響，同時選擇150次傳播過程中節點感染狀態觀測數據（=150）進行處理。結合圖1來說明，圖中完成了不同算法影響關系推斷情況值比較。由此不難發現，當網絡規模持續增大時，所有算法值逐漸減小，而從規模較小、較大的數據集來看，本文算法均表現出較為領先的優勢。結合圖2來說明，圖中完成了Net Rate、本文算法感染傳播概率推斷結果均方誤差比較，隨著網絡規模越來越大，二者均方誤差明顯降低，相比之下本文算法表現更低。

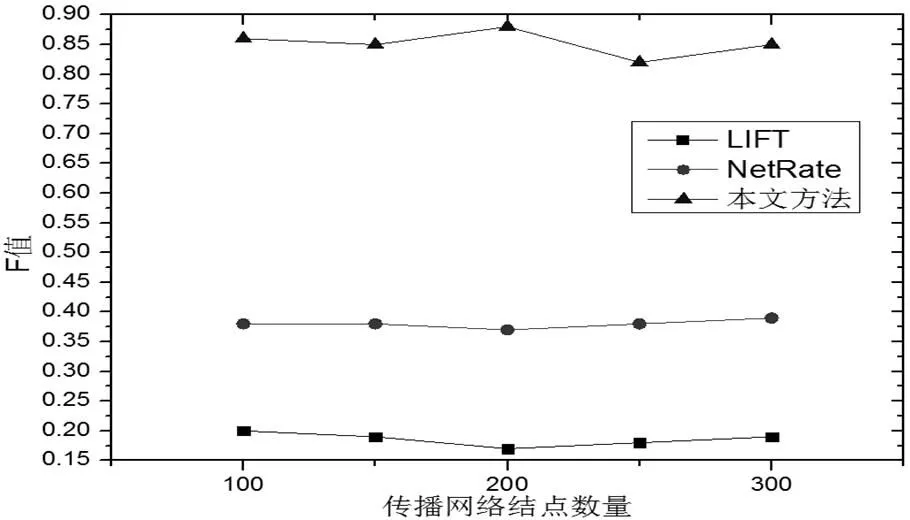
圖 1 傳播網絡節點數量對F值的影響

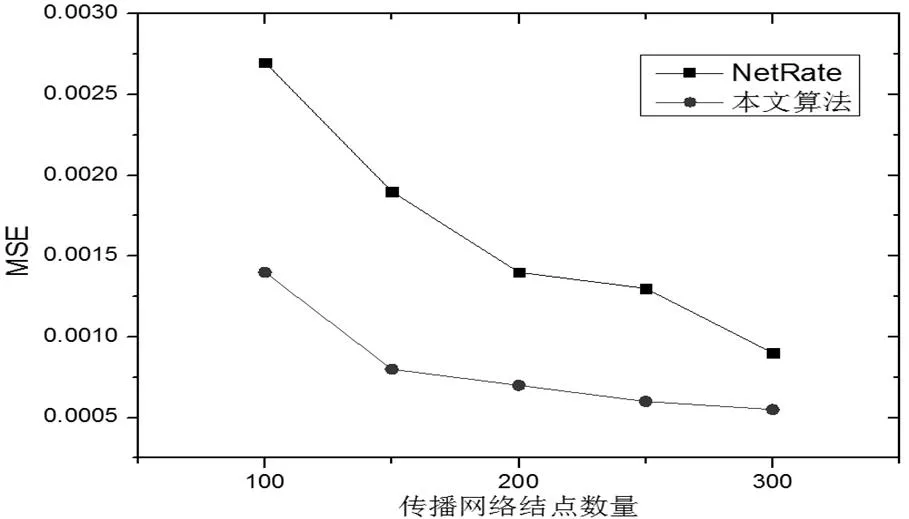
圖 2 傳播網絡節點數量對均方誤差的影響

3.3 初始感染節點比例的影響

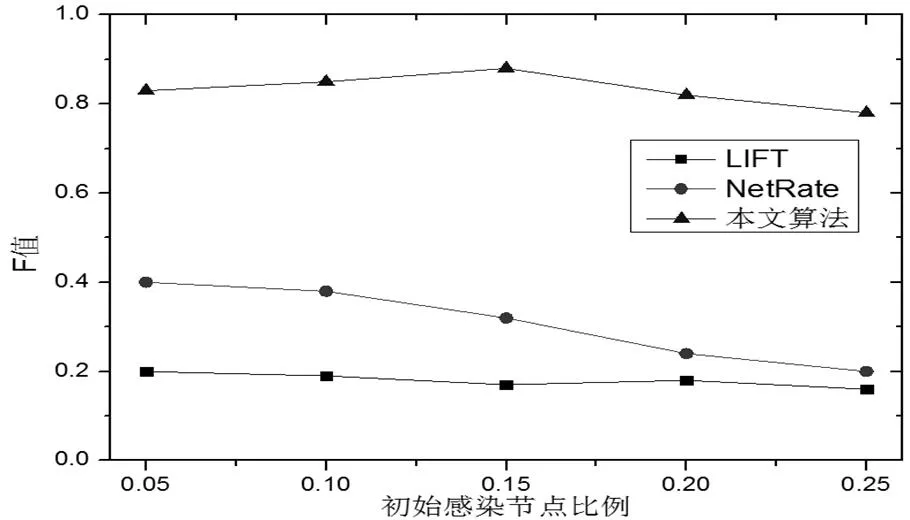
圖 3 初始感染節點比例對F值的影響

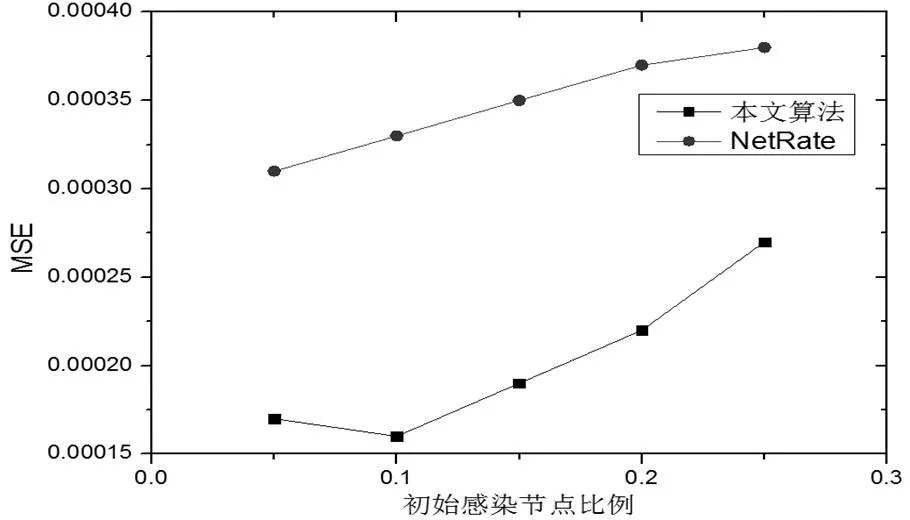
圖 4 初始感染節點比例對均方誤差的影響

4 結語

本文目標在于提出更理想傳播網絡推斷算法，既要保證準確性、高效性，又無須考慮感染時間信息，結合該目標要求，本文首先通過不同節點感染情況間互信息直接量化彼此間內在關聯，由此確定所有可能存在的影響關系。其次，構造出節點感染情況觀測結果（變量是感染傳播概率）相關對數似然函數，通過期望最大化法進行處理，同時計算感染傳播概率。結合實驗分析不難發現，相較當前算法而言，該算法優勢較為明顯，一方面能實現傳播網絡更準確推斷，另一方面能減少執行時間，進一步保證處理效率。

[1] Gomez-Rodriguez M, Leskovec J, Sch?lkopf B. Modeling information propagation with survival theory[C]. Atlanta, Georgia, USA: Proceedings of the 30thInternational Conference on Machine Learning, 2013

[2] Amin K, Heidari H, Kearns M. Learning from contagion (without timestamps)[C]. Beijing, China: Proceedings of the 31stInternational Conference on Machine Learning, 2014

[3] Gomez-Rodriguez M, Sch?lkopf B. Submodular inference of diffusion networks from multiple trees[C]. Edinburgh, Scotland, UK: Proceedings of the 29thInternational Conference on Machine Learning, 2012

[4] Mehmood Y, Barbieri N, Bonchi F,. CSI: Community-level social influence analysis[C]. Prague, Czech Republic: Proceedings, Part II, of the European Conference on Machine Learning and Knowledge Discovery in Databases, 2013

[5] Lancichinetti A, Fortunato S, Radicchi F. Benchmark graphs for testing community detection algorithms[J]. Physical Review E, 2008,78(4):046110

[6] Wang S, Hu X, Yu PS,. MM Rate: Inferring multiaspect diffusion networks with multi-pattern cascades[C]. New York, USA: Proceedings of the 20thACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2014

[7] Gomez-Rodrigue M, Balduzzi D, Sch?lkopf B. Uncovering the temporal dynamics of diffusion networks[C]. Bellevue, Washington, USA: Proceedings of the 28th International Conference on Machine Learning, 2011

[8] Amin K, Heidari H, Kearns M. Learning from contagion(without timestamps)[C]. Beijing, China: Proceedings of the 31st International Conference on Machine Learning, 2014

Study on The Inference Model of Communication Network Based on Node Inconsistency

XU Nan-nan1, HU Chen-guang1, YU Xiao-hui2

1.100176,2.101149,

In order to overcome the communication network node inference cannot be obtained accurately infection time information, firstly the inconsistency between nodes is quantified by infection information between different nodes to determine all the possible influence relationship. Secondly, the logarithmic likelihood function of node infection transmission probability is constructed and calculated by expectation maximization method. The results showed this algorithm was better than current one, on the one hand, it could achieve a more accurate inference for a communication network, on the other hand, it could reduce the execution time and further ensure the processing efficiency.

Communication network; inconsistency; inference model

TP391

A

1000-2324(2019)01-0159-04

10.3969/j.issn.1000-2324.2019.01.036

2018-01-12

2018-03-03

國家自然科學基金項目(71801016);北京電子科技職業學院校內重點課題:基于微信企業號的移動校園服務平臺搭建研究(CJGX2016-KY-YZK030)

徐楠楠(1982-),女,碩士,工程師,主要從事高校信息化建設、數據分析、網絡管理研究. E-mail:xunn0828@sina.com