二維應變作用下超導薄膜LiFeAs的磁性和電子性質*

王鑫 李樺 董正超? 仲崇貴2)?

1) (南通大學理學院, 南通 226019)

2) (蘇州大學物理科學與技術學院, 蘇州 215006)

(2018 年5 月14日收到; 2018 年11 月13日收到修改稿)

基于密度泛函理論的第一性原理計算, 研究了二維應變作用下LiFeAs超導薄膜的磁性結構、電子能帶和態密度變化, 分析了應變對其超導電性的作用. 結果顯示, 對體系施加1%—6%的二維平面張、壓應變均不改變其基態條形反鐵磁性結構, 費米面附近的電子態密度主要來自于Fe-3d軌道電子以及少量的As-4p電子. 研究發現, 與無應變情形相比, 當施加壓應變時, 體系中Fe離子的反平行的電子自旋局域磁矩減小, 薄膜反鐵磁性受到抑制, 費米面上電子態密度增加, 超導電性來自于以反鐵磁超交換耦合作用為媒介的空穴型費米面和電子型費米面間嵌套的Cooper電子對. 而在張應變作用時, 局域反鐵磁性增強, 費米面上電子態密度減小, 金屬性減弱, 特別是張應變時費米面上空穴型能帶消失, Cooper電子對出現概率顯著降低, 將抑制超導相變.

1 引 言

2008年2月, 日本科學家Nomura等[1]率先在鐵基反鐵磁性材料LaFeAsO1-xFx中發現了存在轉變溫度(Tc)為26 K的超導相, 這一突破性發現揭開了磁性超導材料研究的新篇章. 近幾年來, 新型鐵基超導材料的超導機理和特性研究日益成為國內外研究的熱點. 一個普遍的觀點是, 在大多數鐵基磁性材料中, 由于存在具有顯著的自旋密度波, 超導電性通常難以出現[2]. 然而通過對母體的電子(空穴)摻雜或施加外界壓力抑制其自旋密度波行為, 則可能在體系的反鐵磁相界附近產生超導電性, 甚至可將材料的超導臨界溫度實現顯著提升[3,4].

磁性鐵基化合物LiFeAs (LFA)作為超導電性研究的原型材料, 其電子、磁性以及能帶結構與超導機理的關聯受到研究人員的極大關注. Ma等[5]通過核磁共振(nuclear magnetic resonance, NMR)實驗發現, 由于不存在自旋密度波行為, 僅在接近超導轉變溫度時才觀測到原子上很弱的局域磁矩,使得LFA超導體的超導電性出現在不穩定的反鐵磁相界附近. 另一方面, 通過角分辨電子光譜實驗(angle resolved photoemission spectroscopy,ARPES)和非彈性中子散射實驗(inelastic neutron scattering, INS)也發現LFA具有多能帶結構,在倒空間微弱的空穴型費米面和電子型費米面互相嵌套形成具有超導帶隙的拓撲超導態[6-8], 而其準嵌套的電子型和空穴型費米口袋的大小則可以通過高壓或摻雜方式進行調控[9], 進而改變LFA超導薄膜的電子結構和超導特性, 提高其超導相變溫度.

為了深入研究111體系的超導機制以及其超導態的可調控性, Zhang等[10]和Zeng等[11]首先利用高壓技術對樣品施加壓力并結合同步輻射技術,通過壓力調控研究鐵基超導材料的結構及最高超導轉變溫度. 他們發現對于LFA晶體, 在一定壓力范圍之內, 超導轉變溫度Tc隨著壓力的增大、面內As—Fe—As鍵角的增加而降低,Tc與壓力呈現負相關效應, 而NaFeAs晶體的Tc則先增加后減小, 在3 GPa壓力下FeAs4為規則的正四面體結構時Tc達到最大, 表明畸變的FeAs4四面體結構不利于體系的超導[12]. Li等[13]對LFA晶體進行Co離子摻雜, 通過INS以及ARPES數據發現,隨著Co摻雜量增加, LFA晶體中dxy軌道空穴型費米面減小, dxz/dyz軌道空穴型費米面向遠離費米能級的方向移動, 電子型費米面增大, 電子和能帶結構發生顯著改變. 同時, 摻雜之后的LFA材料發生Lifshitz相變, 費米面附近的超導帶隙向費米能級下方移動[14], 表明通過摻雜可以調控LFA晶體的電子結構和超導特性. 雖然通過摻雜和壓力調控鐵基超導材料結構、磁性相變、超導轉變等得到了較多研究, 但關于二維應變作用誘導LFA薄膜超導態變化的研究卻鮮有報道. 我們可以對LFA施加二維應變作用, 通過改變FeAs4四面體的結構對稱性, 調控其電子和能帶結構, 從而調控費米面的能帶嵌套, 這也為LFA的超導特性及機理研究提供了有效途徑.

本文運用基于密度泛函理論的第一性原理計算研究了不同二維應變作用下111體系中LFA的磁性結構、能帶和電子態密度, 分析了應變對LFA超導薄膜超導電性的影響. 通過比較分析LFA材料所有可能的磁性結構, 計算得到體系的基態結構為條形反鐵磁序, 而對其施加大到6%左右的張、壓應力均不改變其磁性結構. 通過對LFA材料的電子態密度和能帶結構的分析發現,費米面附近的電子態密度主要來自于Fe-3d軌道電子以及少量的As-4p電子, 施加壓應變可使其反鐵磁性局域磁矩減小, 磁性減弱, 費米面的上電子態密度顯著增加, 空穴型和電子型能帶的同時出現為超導性提供了Cooper載流子, 而當LFA材料受到張應變作用時, 薄膜性質呈現相反的變化, 反鐵磁性增強, 費米面處態密度值變小, 體系金屬性降低.

2 結構及計算方法

LFA晶體在常溫下為四方晶系結構, 如圖1所示, 空間群為P4/nmm. 原胞中各原子的位置為[15]Li (0.25, 0.25, 0.3325), Fe (0, 0, 0), As (0.25,0.25, 0.1124), 可見FeAs層中的每一個Fe原子與周圍4個As原子形成四面體結構, 而面內的Fe原子形成正方格子. 在該晶體中, 雖然其導電等輸運性質主要來自于FeAs層[16], 但其磁性不僅來源于層中Fe離子的自旋耦合, 層間Fe離子間也存在相對較弱的自旋交換耦合. 考慮到Fe離子間可能不同的交換耦合, 將LFA材料的層內Fe離子分為條形結構和棋盤形結構, 而Fe-Fe層之間又可以分為鐵磁性耦合和反鐵磁性耦合, 如圖2所示, 總共有4種結構, 即條形鐵磁性(FM-1a)、條形反鐵磁性(AFM-2a)、棋盤形鐵磁性(FM-1b)、棋盤形反鐵磁性結構(AFM-2b).

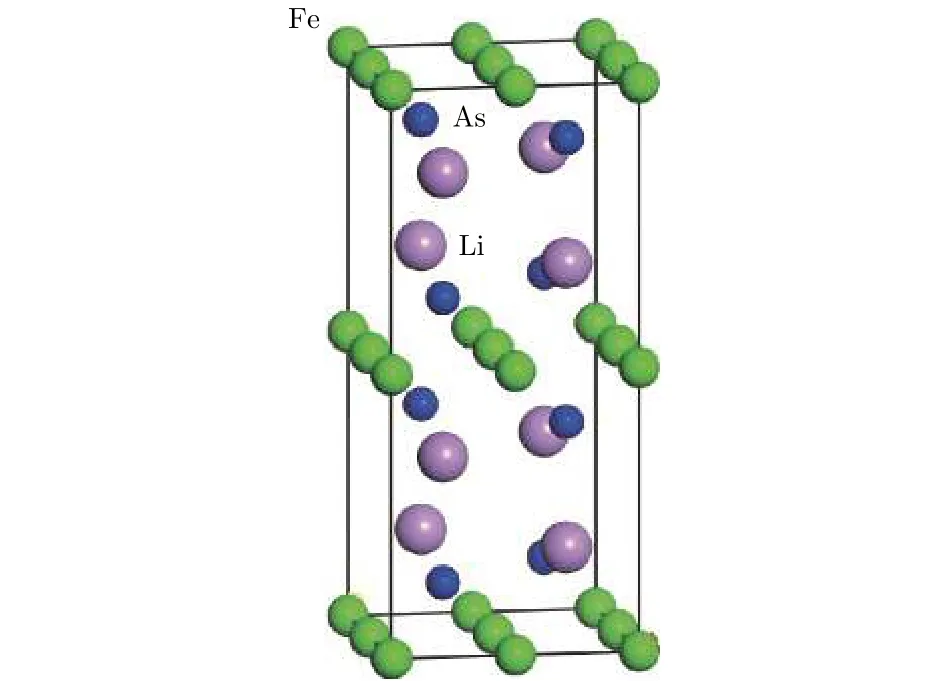
圖1 LFA的晶體結構Fig.1. Crystal structure of LFA film.

計算使用基于第一性原理的VASP程序包進行, 采用全勢線性綴加平面波展開法(full-potential linearized augmented plane wave)描述離子和電子之間的相互作用. 采用基于Perdew-Burke-Ernzerhof 的廣義梯度近似(global gaming alliance)描述交換關聯能, 取2s1, 3d64s2和4s24p3分別作為Li, Fe和As原子的價電子參與計算. 考慮到磁性結構不同導致晶體的周期性擴大, 采用的超原胞模型進行計算. 計算中, 平面波截斷能取為 500 eV (1 eV = 1.602177 × 10-19J),布里淵區中K點取樣為16 × 16 × 12, 自洽計算的能量收斂判據為1 × 10-5eV/atom (1 eV/atom =96.15384615384615 kJ/mol).

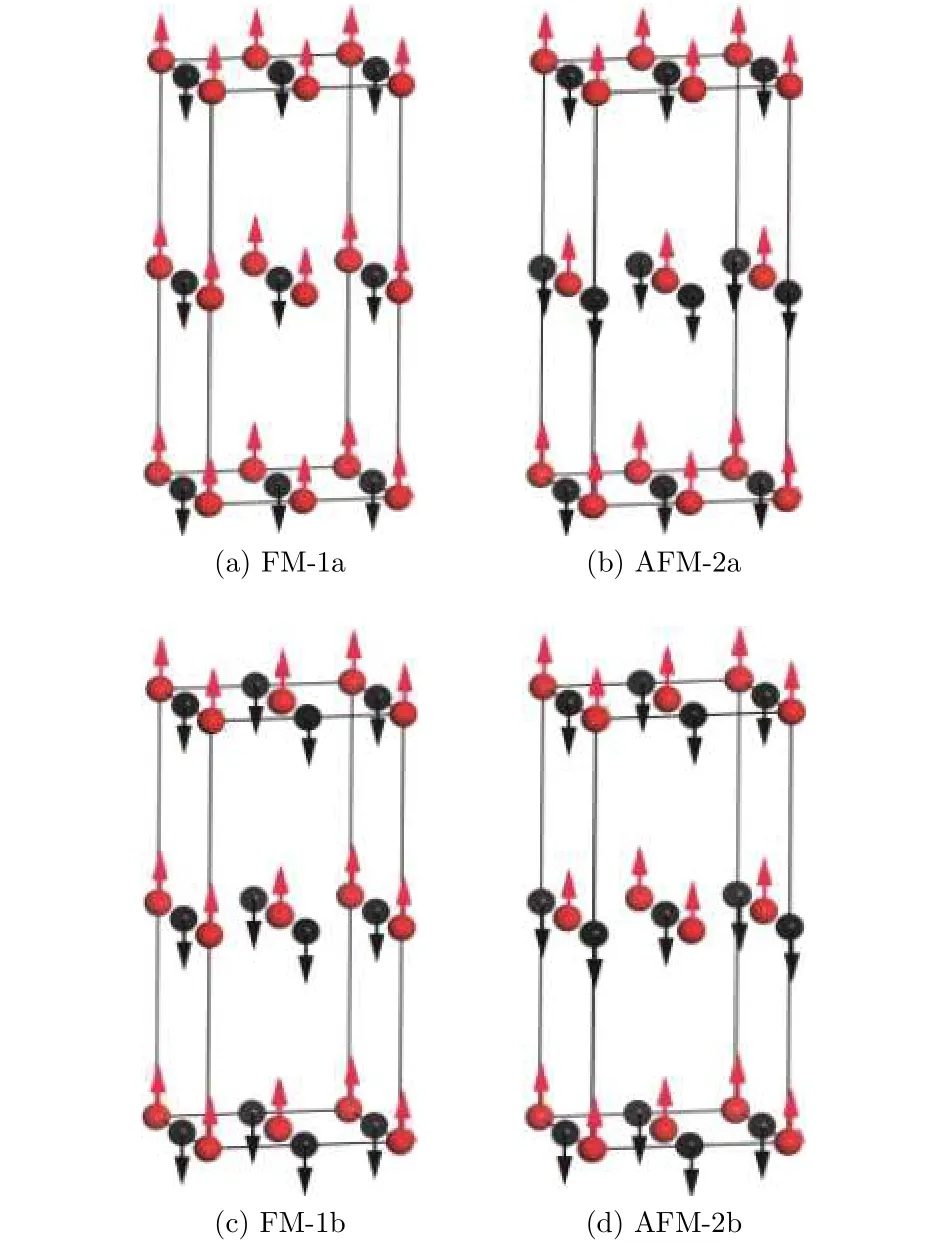
圖2 LFA薄膜中Fe離子可能的四種磁性結構 (a) 條形鐵磁; (b)條形反鐵磁; (c) 棋盤形鐵磁; (d) 棋盤形反鐵磁; 箭頭表示自旋方向Fig.2. Four possible kinds of magnetic structures of Fe ion in LFA thin films: (a) Striped-type ferromagnetic order;(b) striped-type antiferromagnetic order; (c) checkerboardtype ferromagnetic order; (d) checkerboard-type antiferromagnetic order. The arrows represent the directions of electronic spins.

3 結果與討論

首先對LFA晶體進行無磁性的結構優化, 得到其晶格常數分別為a=b= 5.363 ?,c= 12.266 ?,與實驗結果相比, 晶格常數c約小1.53%, 而晶格常數a僅有0.52%的誤差[17], 小的誤差保證了本文結果的正確性. 然后, 基于該優化的晶體結構考慮不同的磁性結構計算, 得到了無應變作用時LiFeAs單胞在4種磁性結構下的能量, 如表1所列. 比較發現, 與其他3種磁性結構相較, LiFeAs晶體的條形反鐵磁性結構(AFM-2a)能量最低, 條形鐵磁性結構(FM-1a)次之, 條形鐵磁的單胞能量比條形反鐵磁高出6.23 meV. 可見LiFeAs薄膜的條形反鐵磁(AFM-2a)結構最穩定, 這與他人實驗和理論預測的LFA基態磁性結構相符合[18],同時也證明了本文計算結果的可靠性.

為了研究二維應變作用對LFA薄膜的磁性和電子結構的改變, 通過改變平面內的晶格常數來實現對上述四種磁性結構施加1%—6%的張應變和壓應變(因為對超導薄膜平面內的拉伸和壓縮應變調控可通過改變超導薄膜與襯底間的晶格失配來實現). 必須指出的是, 對于外延薄膜, 理論上隨著薄膜生長, 晶格失配弛豫導致晶格常數的改變應當與薄膜的厚度相關. 這里, 為簡單考慮, 我們假設薄膜中的應變均勻, 與厚度無關, 二維應變由平面晶格常數的大小決定. 同時考慮LFA薄膜外延生長于四方晶格襯底時, 面內晶格a=b, 而晶格常數c的取值則是根據平面內晶格變化時單胞能量最低來確定. 因為條形反鐵磁單胞能量最低, 這里選取其作為參考態, 不同磁性結構下相對能量隨晶格常數a的變化如圖3所示.

由圖3可以看出, 當LFA超導薄膜的晶格常數發生變化時, AFM-2a磁性態的相對能量總保持最低, 說明張應變和壓應變都不能使LFA材料發生磁性相變, 其基態總是條形反鐵磁結構. 而FM-1a態的相對能量次之, 與AFM-2a相差極不明顯,棋盤形的FM-1b和AFM-2b相對能量均遠高于FM-1a和AFM-2a. 同種類型中的反鐵磁與鐵磁的能量接近, 說明LFA薄膜中Fe離子的層間反鐵磁耦合較弱, 而條形磁結構的能量遠低于棋盤形磁結構則表明層內Fe離子間的反磁性耦合很強, 而且這種強的層內條形反鐵磁以及層間的反鐵磁耦合, 也是應變難以改變的, 這為通過應變調控電子和能帶結構而不改變磁性結構提供了前提.

另外, 從圖3中也可以發現, 施加壓應變時體系能量相對變化比施加張應變時更快, 說明壓應變對體系的作用更明顯. 為了深入研究施加張應變和壓應變對其能帶和電子結構的作用, 下面我們在條形反鐵磁性基態結構下, 分析體系不受應變(a=5.363 ?)和受到3%張應變(a= 5.524 ?)和-3%的壓應變(a= 5.202 ?)時的能帶和電子結構.

圖4(a) 給出的是不受應變作用時的能帶結構,很明顯這是一個金屬型的能帶結構. 之前, 方明虎團隊的實驗研究發現鐵基超導體的母體化合物呈現反鐵磁性[19], 并且可以通過自旋口袋模型解釋[20].在此模型中, 反鐵磁性的具體表現就是電子能帶結構在費米面附近有能隙出現. 依據此模型, 結合圖4(a)可以看到, 在LFA超導薄膜的倒格子第一布里淵區邊緣沿著高對稱X-R方向出現可通過應變調控的能隙. 該能隙的出現表明LFA材料的基態結構具有典型的層間反鐵磁性耦合特點, 這與我們前面得到的材料的基態磁性結構相吻合, 該方向平坦的散射曲線也說明層間的反鐵磁耦合相對較弱. 在高對稱方向Γ-X以及Z-R方向出現兩個開口向下的空穴型能帶, 而且這些空穴型能帶明顯表現出較強的散射特性, 表明層內Fe離子間的電子自旋存在強的交換耦合. 這種強磁性交換耦合作用既包括了條帶間離子的反鐵磁性耦合, 也包括了條帶內相鄰Fe離子間電子自旋間的鐵磁性交換作用. 而面內能隙的消失則應該是由于條帶內鐵磁性的耦合作用所致. 但是, 能帶中無電子型能帶的出現, 說明無應變時LFA條形的反鐵磁基態中的金屬導電性強弱完全依賴于空穴濃度的高低.

表1 無應變時鐵基超導薄膜LFA不同磁性結構下的單胞能量Table 1. Energy of unit cell of the iron-based superconductor thin film LFA in different magnetic structures.

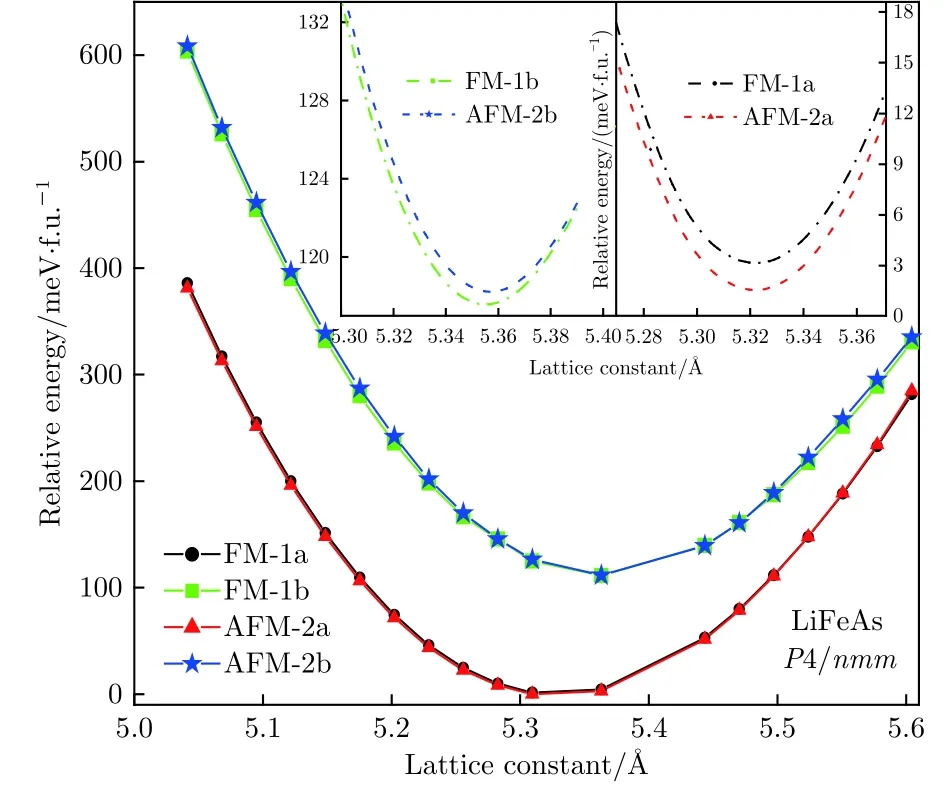
圖3 LiFeAs薄膜中四種磁性結構的相對能量隨晶格常數的變化Fig.3. Relative energies of different magnetic states varying with lattice constant of LFA thin film.

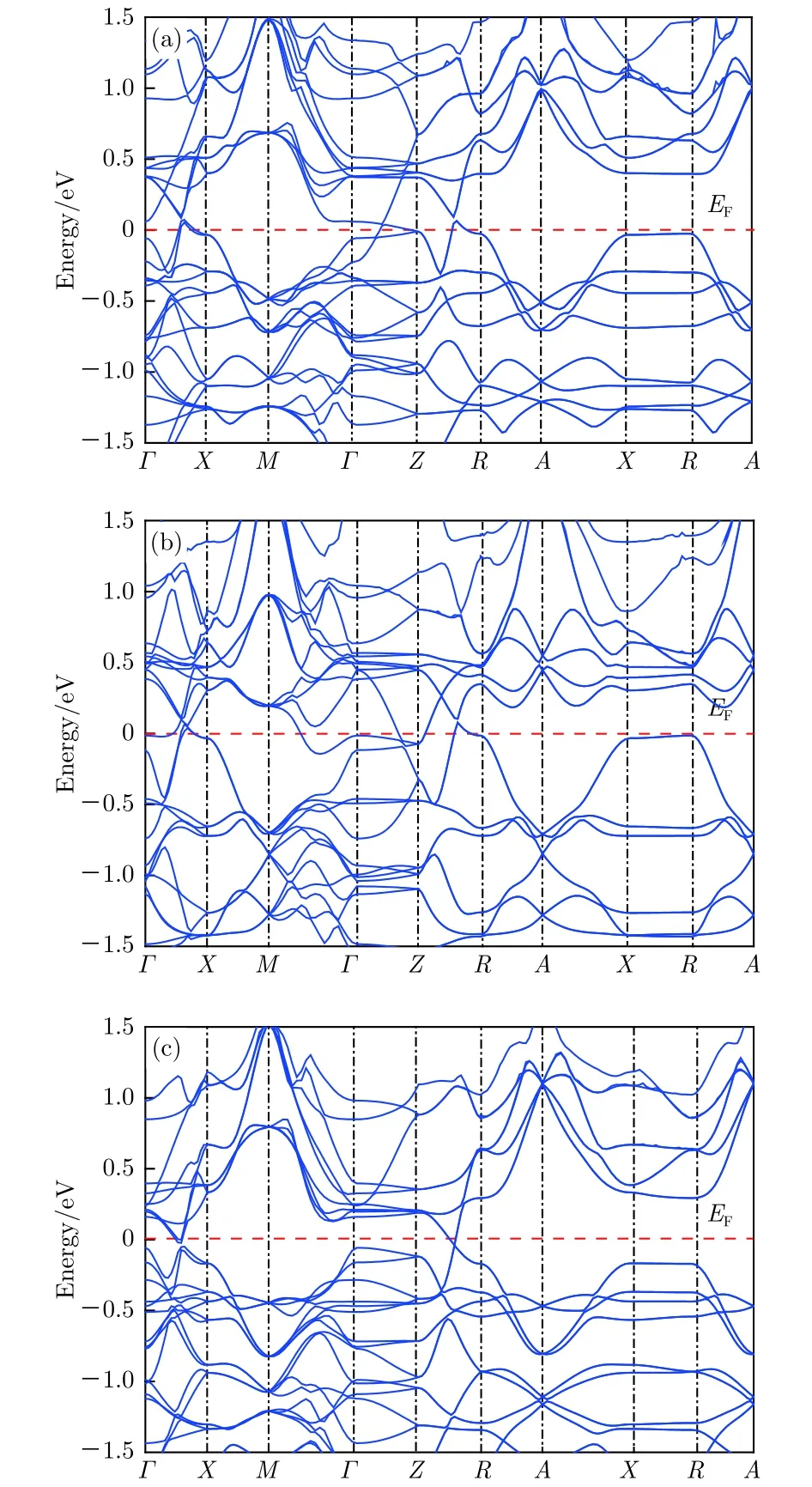
圖4 LFA超導薄膜AFM-2a磁性結構在不同應變條件下的能帶結構 (a)無應變; (b) 壓應變(-3%); (c) 張應變(3%)Fig.4. The band structure of LFA superconductor thin film (AFM-2a magnetic states) under different strains:(a) Nostrained effect; (b) compressive strain (-3%);(c) tensile strain (3%).

應變作用下LFA薄膜能帶發生了顯著變化,如圖4(b)和圖4(c)所示. 與沒有發生應變的圖4(a)相比, 當LFA超導膜受到-3%壓應變時(見圖4(b)),雖然空穴型能帶數目沒有增加, 但是費米能級之上的能帶顯著向下移動, 導致沿著高對稱性Γ-M和Γ-Z方向, 特別是在Z點出現兩條開口向上的電子型能帶, 費米面上的電子態密度增加. 這樣, 在二維壓應變作用下的反鐵磁性LFA超導薄膜中,不僅存在空穴導電, 還存在態密度更大的電子導電, 因此我們可通過增強二維壓應變作用, 提高電子型能帶在費米能級處的態密度來增強鐵基超導LFA薄膜的金屬性, 從而實現可能的超導電性. 這與在實驗中通過對鐵基超導材料LaOFeAs, BaFe2As2施加外加壓力來提升超導電性的方法[21]較為一致.然而, 如果外加二維的張應變, 能帶結構就會發生相反的變化, 如圖4(c)所示. 相對于無應變時的能帶, 這時我們發現能帶整體下移, 空穴型電子能帶消失,Γ點以及X-R方向的能隙增加, 費米面處的電子態密度顯著減小, 從后面的電子態密度圖中也可以發現這一點. 這表明張應變使體系的金屬性減弱, 不利于實現LFA薄膜的超導電性. 根據實驗研究數據, 費米能上電子態密度的抑制是導致LFA超導相變溫度下降的主要原因[22].

費米面上電子態密度的增加或減少, 與二維壓應變或張應變導致層內和層間的磁性交換耦合作用改變密切相關. 在平面壓應變作用下, 層間的晶格常數增大, 反鐵磁性交換耦合減弱, 而層內晶格常數減小, 條帶內最近鄰鐵磁性交換耦合J1以及條帶間最近鄰的反鐵磁交換耦合J1′都同時增強, 但由于層內四個次近鄰的Fe—Fe之間反鐵磁耦合J2是通過As離子實現的超交換作用, 這種超交換耦合的性質和強弱與Fe—As—Fe的鍵角大小密切相關. 壓應變使得面內晶格常數減小的同時, 原先扁平的FeAs4四面體逐漸向正四面體結構畸變, 層內As—Fe—As和Fe—As—Fe鍵角減小, Fe—Fe之間的超交換耦合有向雙交換耦合轉變的趨勢. 因此, 整體上單胞內反鐵磁性耦合減弱, 鐵磁性耦合增強, 但體系仍然以反鐵磁性耦合為主. 也就是說壓應變的增加使得體系更臨近反鐵磁耦合-鐵磁耦合轉變相界, 因此更容易誘導超導相, 這也驗證了材料LFA或NaFeAs在加壓作用下的結果[23]. 而外加張應變的結果正好相反, 張應變使得Fe—As—Fe的鍵角增大, 反鐵磁交換耦合增強, 鐵磁性減弱, 費米面上電子態密度顯著減小, 超導薄膜的金屬性變差, 不利于超導性相變.

另一方面, 根據磁性計算, 我們得到了不同應變作用下Fe離子的自旋磁矩, 如表2所列. 可見,壓應變作用使得Fe離子的總磁矩mt明顯增大, 而張應變則使Fe離子總自旋磁矩減小. 壓應變作用下的總磁矩增加, 似乎導致體系的反鐵磁性增強,這對于促進超導電性的相變極其不利. 然而, 進一步的數據分析發現, 壓應變下的磁矩增加主要來自于費米面巡游電子的磁矩mi增加; 與無應變作用相比, 此時反鐵磁耦合的局域磁矩ml卻由1.345μB(1μB= 9.27400949(80) × 10-24J·T-1)減 小 到1.324μB. 另一方面, 雖然張應變作用下的Fe離子總自旋磁矩從無應變時的 1.532μB減小到1.414μB, 但這個降低主要是由于費米面上巡游電子磁矩的顯著降低導致, 而局域磁矩則由1.345μB增加到1.388μB. 這些變化也可以從圖5中不同應變作用下電子態的自旋劈裂情況分析得到. 外加張應變使得局域反磁性增強, 超導相變受到抑制, 而壓應變作用則導致體系的反鐵磁性壓制, LFA薄膜向有利于超導相變的方向發生. 而且, 根據超導電性源于費米面附近形成的Cooper電子對理論[24],發生在近鄰Fe—Fe原子間以反鐵磁超交換耦合作用為媒介的空穴型能帶和電子型能帶間的Cooper電子對, 為壓應變作用有利于誘導超導電性的形成提供了理論支撐. 而對于無應變或者張應變作用, LFA的費米面處只存在電子型或空穴型能帶, 難以形成電子的Cooper配對.

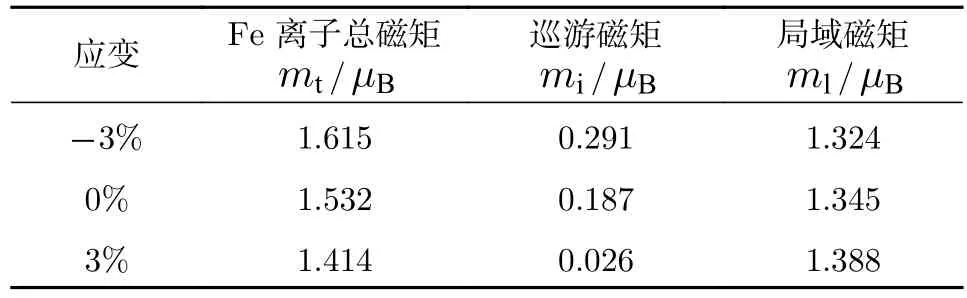
表2 不同應變作用下LFA薄膜中Fe離子的自旋磁矩Table 2. Magnetic moments of Fe ions of LFA thin films under different strains.

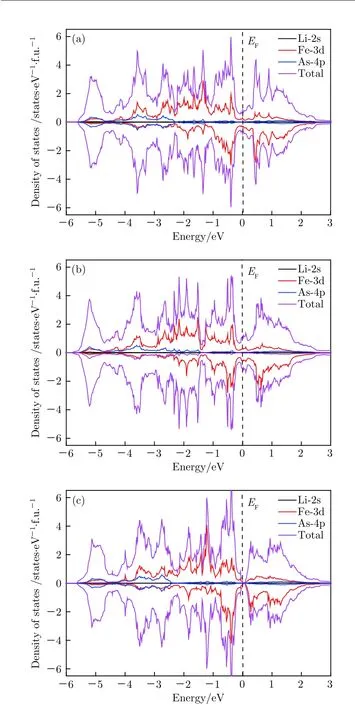
圖5 LFA超導薄膜在不同應變條件時各離子的電子態密度 (a) 無應變; (b) 壓應變(-3%); (c) 張應變(3%)Fig.5. The density of electronic states of different ions in LFA superconductor thin film under different strains:(a) Nostrained effect; (b) compressive strain (-3%);(c) tensile strain (3%).

因此, 為了具體分析不同應變作用下費米面附近電子態的變化情況, 我們也分別給出了LFA在無應變、-3%壓應變和3%張應變情況下的電子態密度分布, 如圖5所示. 不難發現, 無論是否存在應變, 在能量-6—3 eV之間, Fe-3d的電子態密度與總態密度的分布幾乎一致, 且其態密度值僅次于總能態密度值, 表明LFA費米面附近電子態主要來自于Fe-3d電子. As-4p軌道電子則主要局域在費米面以下-5—-3 eV, 且 Fe-3d和 As-4p電子之間存在較強程度的雜化[25], 說明Fe離子之間的電子自旋交換耦合是通過As離子來實現的,而Li-2s電子對費米面的貢獻很小, 可以忽略不計,這一點在實驗中已經得到證實[26]. 摻雜或者加壓的數據顯示, LFA費米面附近電子態來自Fe-3d以及少部分As的4p電子雜化[27], 顯然在二維應變作用下, 費米面附近的這種雜化相比于其低能區要微弱得多.

與圖5(a)中LFA超導薄膜沒有發生應變的電子結構相比, 當受到-3%的壓應變作用時, 費米面-下4—-0.25 eV能量范圍內, 電子自旋劈裂減弱, 可見局域自旋磁矩減小, 反鐵磁性耦合被抑制,而費米能級處總的電子態密度隨著Fe-3d態密度值的增加而增加, 見圖5(b). 這是因為壓應變作用使得原先扁平的As四面體結構逐漸向正四面體畸變過程中(見圖6), t2g能級與 eg能級間隔相對減小, Fe離子3d軌道的電子分布更趨于均勻, 在費米面下-3.5 eV左右處Fe-3d和As-4p之間的軌道雜化減弱, 參與形成Fe—As共價束縛的電子數減少, 更多的Fe-3d電子填充 t2g態故而發生巡游變化, 原來貢獻Fe離子磁矩的局域3d電子一部分變為巡游電子[28], 導致FeAs層中的載流子數增多, 從而費米面上的電子態密度增加. 巡游電子數的增加, 貢獻了更多的電子自旋, 因此壓應變作用下Fe離子總磁矩的增大主要來自于巡游電子數的增多. 這與其他鐵基超導材料計算得到的結果相符合[29]. 相反, 在圖5(c)中, LFA超導薄膜受到3%張應變作用時, 費米能級處總的電子態密度則隨著Fe-3d態密度值的減小而減小. 費米能處Fe-3d態提供的巡游電子數減少, 電子的巡游磁矩mi顯著降低. 同時, 由于費米能以下處于束縛態的Fe離子核外3d電子的自旋劈裂顯著增強, 導致體系的局域磁矩增大, 反鐵磁性耦合增強, 從而抑制超導電性形成, 進而也影響材料的超導臨界溫度[22].可以推測, 與受到3%張應變相比, -3%壓應變作用可通過改變能帶結構從而更好地激發LFA薄膜的超導特性. 所以, 我們可通過對LFA薄膜施加二維壓應變, 誘導其超導特性以及為提高其臨界相變溫度提供可能.

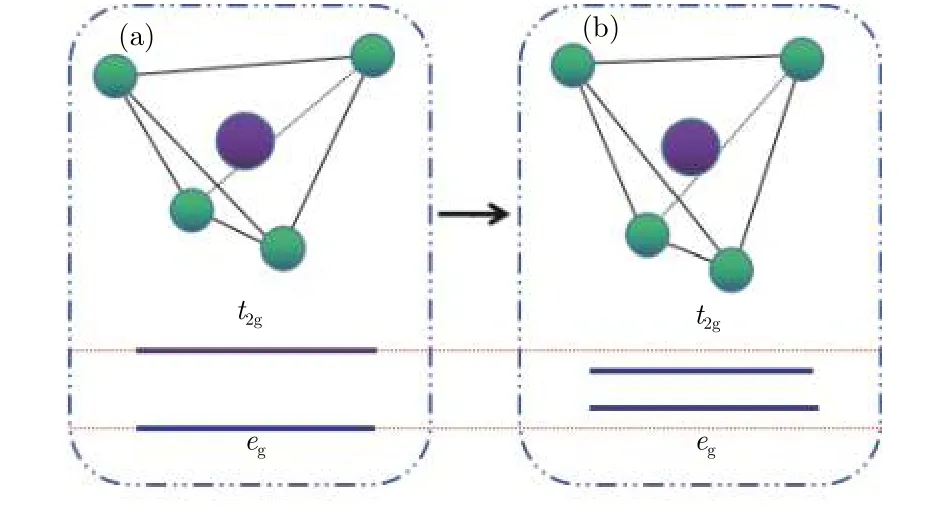
圖6 以Fe離子為中心的As四面體結構畸變與3d軌道能級分裂 (a) 無應變時扁平的四面體; (b) 壓應變作用下畸變后的正四面體Fig.6. The tetrahedral structure distortion of As centered on Fe ions and 3d orbital energy splitting of Fe ions:(a) Tabular tetrahedron without strain effect; (b) the distorted regular tetrahedron under compressive strain effect.

4 結 論

對新型111體系鐵基超導LFA薄膜在不同二維應變作用下的磁性結構、能帶和電子性質進行了詳細的分析, 得到了體系基態時的條形反鐵磁性結構, 并且發現對該LFA薄膜施加6%左右的張、壓應變均不能使條形反鐵磁性結構發生改變. 通過對體系的能帶結構和磁矩變化分析發現, 二維壓應變驅動體系能帶費米面附近同時出現空穴型和電子型能帶, 費米面上電子態密度的增大, 而且由于Fe離子局域3d電子的一部分變為巡游電子, 使得Fe離子的磁矩增大, 但反鐵磁性耦合減弱使得局域的自旋磁矩減小, 體系的反鐵磁性受到抑制.這樣大量的通過反鐵磁性交換耦合的費米面附近的Cooper電子對提供了超導電性的載流子, 有助于提高超導相變溫度. 而在張應變作用下, 體系局域磁矩增大, 反鐵磁性增強, 費米能級上電子態密度減小, 金屬性減弱, Cooper電子對難以形成, 抑制了材料的超導相變.