基于變分模態分解與多尺度排列熵的生物組織變性識別*

劉備 胡偉鵬 鄒孝 丁亞軍 錢盛友

(湖南師范大學物理與電子科學學院, 長沙 410081)

(2018 年9 月26日收到; 2018 年10 月26日收到修改稿)

根據高強度聚焦超聲(HIFU)治療中超聲散射回波信號的特點, 本文利用變分模態分解(VMD)與多尺度排列熵(MPE)對生物組織變性識別進行了研究. 首先對生物組織中的超聲散射回波信號進行變分模態分解, 根據各階模態的功率譜信息熵值分離出噪聲分量和有用分量; 對分離出的有用信號進行重構并提取其多尺度排列熵; 然后通過Gustafson-Kessel (GK)模糊聚類確定聚類中心, 采用歐氏貼近度與擇近原則對生物組織進行變性識別. 將所提方法應用于HIFU治療中超聲散射回波信號實驗數據, 用遺傳算法對多尺度排列熵的參數優化后, 對293例未變性組織和變性組織的超聲散射回波信號數據進行了多尺度排列熵分析, 發現變性組織的超聲散射回波信號的多尺度排列熵值要高于未變性組織; 多尺度排列熵可以較好地識別生物組織是否變性. 相對于EMD-MPE-GK模糊聚類以及VMD-小波熵(WE)-GK模糊聚類變性識別方法, 本文所提方法中變性與未變性組織特征交疊區域數據點更少, 聚類效果和分類性能更好; 本實驗環境下生物組織變性識別結果表明, 該方法的識別率更高, 高達93.81%.

1 引 言

高強度聚焦超聲(high intensity focused ultrasound, HIFU)治療是一種新的無創腫瘤治療技術. 它通過聚焦方式將聲能聚集于治療靶區, 使靶區產生高溫, 從而使病變組織細胞內的蛋白質發生固化、變性和壞死, 同時又不損傷靶區之外的正常組織. 通過監測生物組織的變性情況, 能掌握HIFU的治療效果, 對確保HIFU治療的安全高效有重要意義[1-3]. 迄今為止, 超聲領域的研究人員從多個方面對所取得的超聲信號進行研究, 期望提取出能準確反映組織損傷變性的特征參數, 如回波能量、聲衰減系數、頻率偏移、聲速和熵等[4-8]. 當組織溫度升高到65 ℃以上時, 背散射信號能量會發生顯著變化[4-9]. Seip和Ebbini[10]采用回波信號的能量特征來檢測組織損傷變性, 實驗結果表明,信號能量識別準確率達到82%. 在文獻[11]中, 生物組織的超聲衰減系數特征被用于估計組織損傷區域的溫度. 盛磊等[6]利用頻率偏移等特征參數檢測HIFU導致的組織凝固性壞死. 聲速可以非侵入式地估計組織溫度, 但是聲速受非線性以及熱膨脹的影響, 導致通過聲速變化測量體內溫度的準確性大大降低[7-12]. 明文等[8]采用超聲散射回波信號的小波熵(wavelet entropy, WE)特征對HUFU治療過程中的組織損傷變性進行評價研究, 同時對組織樣本進行損傷級歸類. 但到目前為止, 將超聲回波信號的多尺度排列熵(multi-scale permutation entropy, MPE)特征用于生物組織變性識別是否有效的研究還未見報道.

經驗模態分解(empirical mode decomposition,EMD)是將一個時間序列信號分解成一組有限的本征模態函數[13], 并且文獻[14]已經將其應用至從人體獲得的超聲回波信號, 然而, EMD存在端點效應、模態混疊問題[15]. 為了解決上述問題,Dragomiretskiy和Zosso[15]提出一種新的變分模態分解(variational mode decomposition, VMD)方法, 能較好地抑制信號EMD過程中的端點效應和模態混疊現象, 對噪聲具有更強的魯棒性.

從非線性角度分析生物組織中獲取的信號, 生物組織的損傷變性會導致信號的復雜度不同. 目前非線性分析算法可以通過其熵值有效地分析信號的復雜度, 例如尺度熵、近似熵、多尺度熵等[16-18].排列熵作為一種非線性分析算法, 具有計算簡單、抗噪能力強、魯棒性強的優點, 因此被廣泛應用于時間序列的復雜性分析中[19]. 多尺度排列熵將多尺度和排列熵結合起來, 可以更加有效地分析序列信息[20,21]. 本文從非線性角度分析生物組織中的超聲散射回波信號, 利用多尺度排列熵算法研究未變性生物組織和變性生物組織超聲散射回波信號的差異, 為HIFU治療診斷提供有效的依據和幫助. 然而, 若MPE算法中嵌入維數和尺度因子參數設置不合理, 將導致算法無法達到最佳的處理效果. 同時, 由于生物組織從未變性狀態到變性狀態的演變是一個漸變的過程[22], 因此提取的組織變性特征具有一定的模糊性, GK模糊聚類算法為解決這類問題提供了一條有效途徑[23].

本文結合VMD與MPE算法的優點, 對生物組織變性的特征進行提取, 同時采用遺傳算法確定多尺度排列熵尺度因子參數, 討論了本實驗環境下多尺度排列熵的最佳嵌入維數; 并用GK模糊聚類算法實現了生物組織變性的識別分類.

2 原理與方法

2.1 VMD理論

VMD是一種基于維納濾波, 希爾伯特變換和外差解調的新型多分量信號分解算法. VMD可以將一個實際信號f(t) 分解成K個離散的模態μk(k=1,2,3,···,K), 與EMD算法不同,μk在頻域中的帶寬都具有特定的稀疏屬性, 是調幅調頻(AM-FM)信號, 可以有效地抑制EMD中出現的模態混疊現象. 每個μk緊湊圍繞相應的中心頻率,并且其帶寬通過高斯平滑解調獲得. VMD處理過程中的約束變分問題為

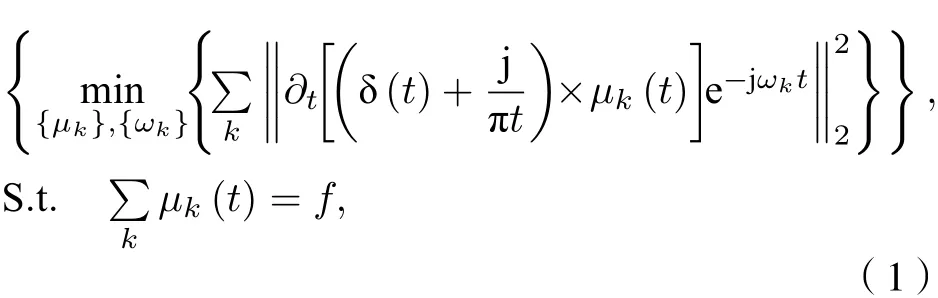
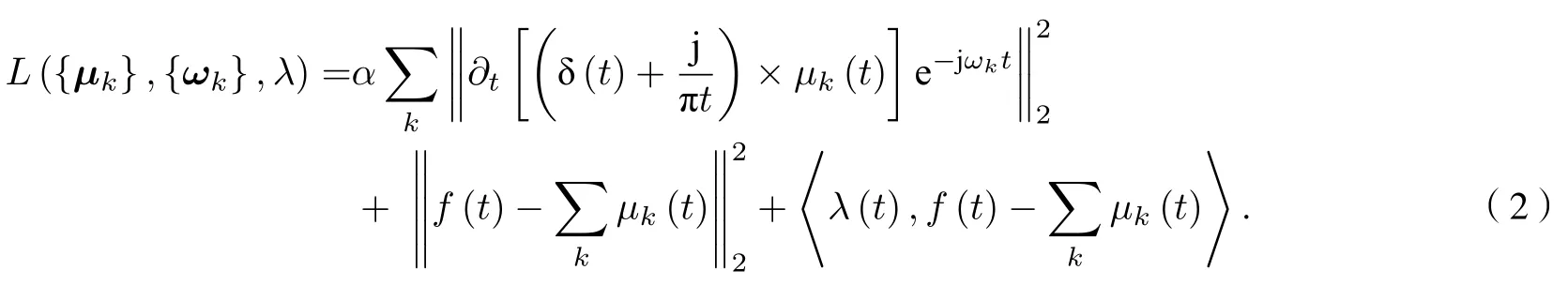
VMD將信號分解為K個模態分量的具體步驟如下:

1) 初始化

2)μk和ωk分別由(3)式和(4)式迭代更新:

3) 根據(5)式更新λ:

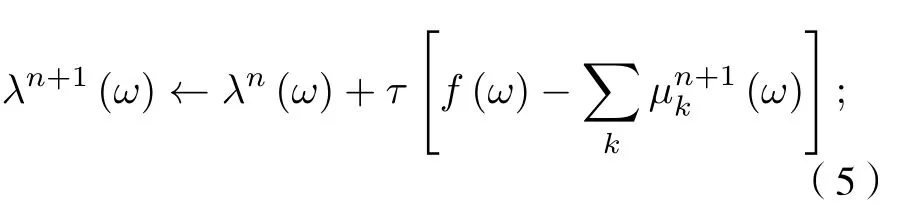
4) 重復步驟 2)和 3), 直至滿足迭代終止條件

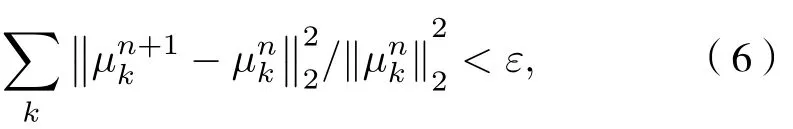
式中ε為判別精度,ε＞0 ;

5) 輸出結果, 得到K個模態分量.

2.2 功率譜信息熵

基于功率譜信息熵判斷各模態分量為有效超聲散射回波信號還是噪聲以及無效超聲散射回波信號的方法流程如下.

1) 計算各模態的功率譜, 并對幅值進行歸一化.

2) 根據歸一化后功率譜的最大值和最小值,得出功率譜的變化范圍. 對功率譜的變化范圍進行分段. 例如, 若信號歸一化后功率譜幅值的變化范圍是0—1, 分成10段, 那么幅值范圍為0—0.1為第一段, 0.1—0.2為第二段, 依次類推.

3) 統計每一段在功率譜幅值中出現的次數,并求出該段在整個數據點中出現的概率.

4) 按照(7)式求解信息熵, 并根據熵值判斷該模態是否為噪聲分量或無效超聲散射信號:

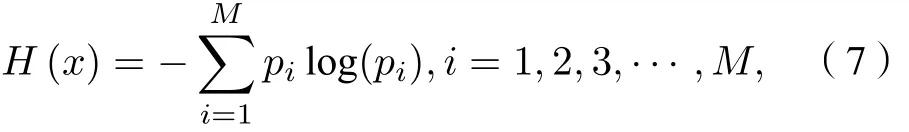
H(x)為功率譜信息熵, 其中pi表示功率譜分段后第i段所對應的概率,M表示總共的分段數.

2.3 多尺度排列熵

多尺度排列熵是在排列熵基礎上的改進, 基本思想是將時間序列進行多尺度粗粒化,然后計算其排列熵. 計算具體步驟如下.

1) 對序列長度為N的時間序列X={xi,i=1,2,···,N}進行粗粒化處理, 得到粗粒化序列y(s)j

得到粗粒化序列

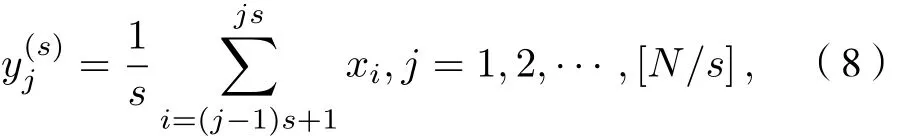
式中s為尺度因子; [N/s]表示對N/s取整.

2) 對y(s)進行時間重構得到

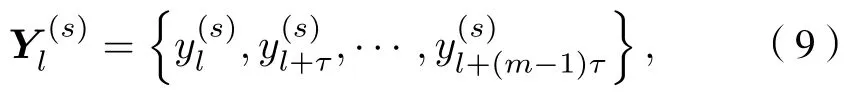
其中m為嵌入維數,τ為延遲時間;l為第l個重構分量,l=1,2,···,N-(m-1)τ.

4) 根據(10)式計算每個粗粒化序列的排列熵, 由此得到時間序列在多尺度下的排列熵.

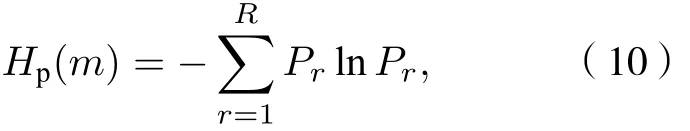
當Pr=1/m! 時 ,Hp(m) 達 到 最 大 值 l n(m!) ; 通 常將多尺度排列熵值Hp(m) 進行歸一化處理, 即

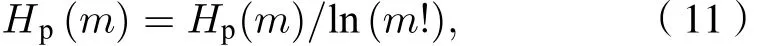
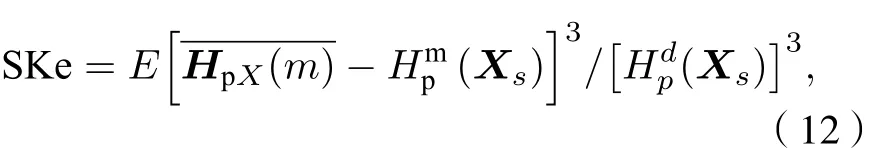
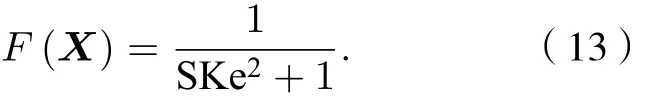
2.4 GK聚類與變性識別

GK模糊聚類算法是利用協方差矩陣能自適應動態度量的模糊聚類算法, 假設輸入數據為GK模糊聚類的目標函數為

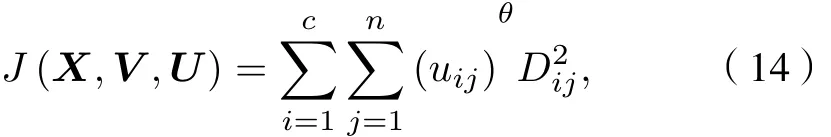
式中θ≥1 為模糊指數, 模糊指數會影響聚類效果,其值太大會導致各類之間相互重疊;Dij為第j個樣本與第i類聚類中心的馬氏距離,Di2j是一個平方內積范數.

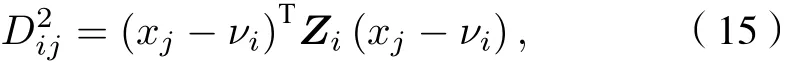
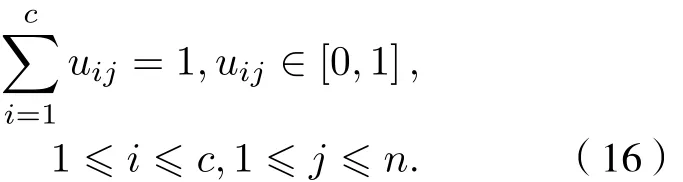
利用拉格朗日乘法對目標函數進行優化, 使(14)式取得極小值, 其必要條件為

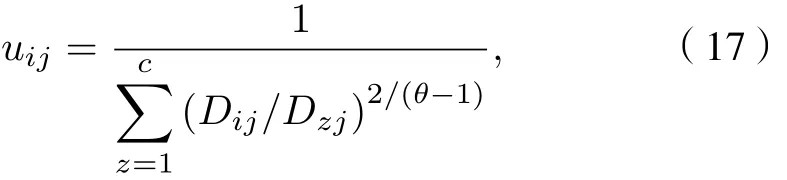
GK模糊聚類算法的具體步驟如下:

1) 確定聚類中心數目c以及模糊指數θ, 根據(16)式對隸屬度矩陣U進行初始化, 通過(18)式計算聚類中心νi;

2) 計算協方差矩陣Fi

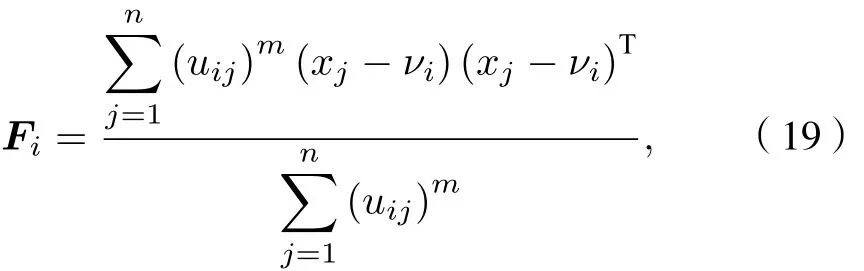
由協方差矩陣Fi求出正定對稱矩陣Zi, 之后根據(15)式計算出平方內積范數利用得到的平方內積范數根據(17)式更新隸屬度矩陣U,若不滿足則增加迭代次數,若滿足判斷式, 則終止迭代運算.

GK模糊聚類的聚類效果可用劃分系數和Xie-Beni (XB)指數進行檢驗.

劃分系數為

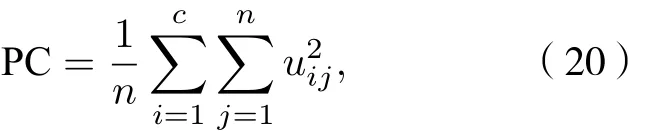
Xie-Beni指數為

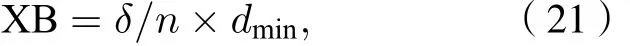
式中δ為類的平均方差,dmin是類間最短模糊距離;對于聚類效果評價, 其中PC越接近1, 代表劃分越清晰, 反之劃分越模糊; XB越小, 代表類間分離的聚類就越好.

本文采用歐氏貼進度和擇近原則實現組織變性模式識別. 貼近度越大, 代表兩個模糊子集的相近程度越大. 對于待識別樣本模糊子集A、標準聚類中心模糊子集B, 其計算如下:

3 模擬仿真及應用實例

3.1 信號分解與去噪

為研究EMD與VMD算法對噪聲的魯棒性,對含噪仿真信號進行分析, 所采用的仿真信號表達式為cos(2π·288t)+η, 其中η為高斯白噪聲, 標準偏差取0.1. 仿真信號及各對應成分如圖1所示.

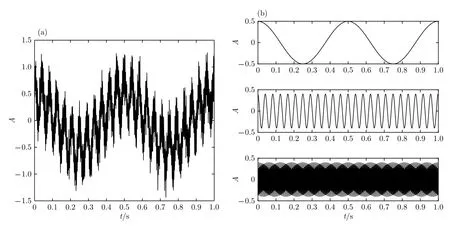
圖1 仿真信號及其對應非噪聲成分的時域圖 (a)加入噪聲的仿真信號時域圖; (b)對應非噪聲成分的時域圖Fig.1. Time-domain diagram of the simulated signal and its non-noise components: (a) Time-domain diagram of the simulated signal with added noise; (b) time-domain diagram corresponding to non-noise components.

圖2為加入噪聲的仿真信號經EMD和VMD處理后的結果. 由圖2(b)可以明顯看出, 隨著EMD分解層數增多, 分解結果出現嚴重失真, 產生虛假分量, 即模態混疊現象. 而根據圖2(a)的VMD結果, 發現分解得到的前三個單頻模態分量與原信號對應各成分比較一致, 說明VMD可以較好地解決信號分解過程中的模態混疊現象, VMD對噪聲具有較強的魯棒性.

圖3(a)為實驗獲得的超聲回波信號. 實驗中用HIFU輻照新鮮離體豬肉組織來改變其特性, 通過B超監控來獲取超聲回波信號, 并經數字示波器(Model MDO3032; Tektronix)轉化為數字信號后進行保存. B超探頭的中心頻率為3.5 MHz. 預先設定VMD算法中的分解模態的個數K= 5, 超聲回波信號經VMD算法分解后, 不同K值下各模態分量如圖3(b)所示.

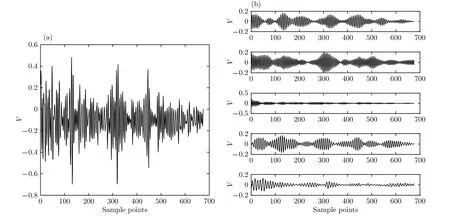
圖3 實際超聲回波信號與VMD結果 (a)實際超聲回波信號; (b)超聲回波信號VMD結果Fig.3. Actual ultrasonic echo signals and their VMD results: (a) Actual ultrasonic echo signals; (b) VMD results of ultrasonic echo signals.

對于每個模態分量, 其對應的功率譜信息熵值越小, 就表示是噪聲分量或無效超聲散射回波分量的概率越大, 反之就認為其中含有用超聲散射回波分量概率越大. 在本實驗環境下得到的超聲散射回波信號經過VMD算法分解得到各階模態分量, 計算各模態的功率譜, 利用2.2節的方法得出各模態的功率譜信息熵. 實驗發現各模態分量的功率譜幅值分段數為16—21時, 噪聲分量、無效超聲散射回波模態分量與有用超聲散射回波模態分量區分效果最佳. 對于本實驗環境下的293例超聲回波數據經過VMD得到的各階模態分量, 其中噪聲分量和無效超聲散射回波信號模態分量的功率譜信息熵在0.028—0.055之間; 如果模態分量中含有明顯的散射信號波形, 其功率譜信息熵在0.13—0.35之間. 上述兩類模態分量功率譜信息熵值的差異, 可以較好地區分噪聲分量、無效超聲散射回波模態分量和有用超聲散射回波模態分量.

3.2 多尺度排列熵的計算

通過篩選功率譜信息熵值在0.13—0.35的模態分量對信號進行重構, 對重構后的信號進行參數優化后的MPE分析, 利用遺傳算法來優化尺度因子s. 參數設置為: 最大進化代數為100; 種群最大數量為20; 交叉概率為0.4; 變異概率為0.09; 超聲回波信號的截取點數為675, 一般來說, 嵌入維數m通常取3—8, 延遲時間τ=2 . 對重構后的超聲散射回波信號進行尺度因子參數優化, 取整后得到多尺度排列熵算法的尺度因子優化參數. 三組樣本的MPE參數優化結果: 第一組和第二組樣本的MPE分析中, 尺度因子參數為12; 第三組樣本的MPE分析中, 尺度因子參數為13.

每組樣本包括總共15例超聲回波信號數據,其中未變性狀態8例, 變性狀態7例. 圖4為嵌入維數m分別取3, 5和7時樣本1的MPE隨尺度因子的變化情況.

從圖4可以明顯看出, 嵌入維數m= 3和5時, 變性組織與未變性組織各尺度因子下的MPE值有較多交疊, 此時MPE不能較好地區分變性組織和未變性組織; 而嵌入維數m= 7時, 變性組織和未變性組織的MPE值有明顯區別, 變性組織的多尺度排列熵值要明顯高于未變性組織的熵值. 表1為嵌入維數為7時, 三組樣本中變性與未變性組織的各尺度排列熵平均值.

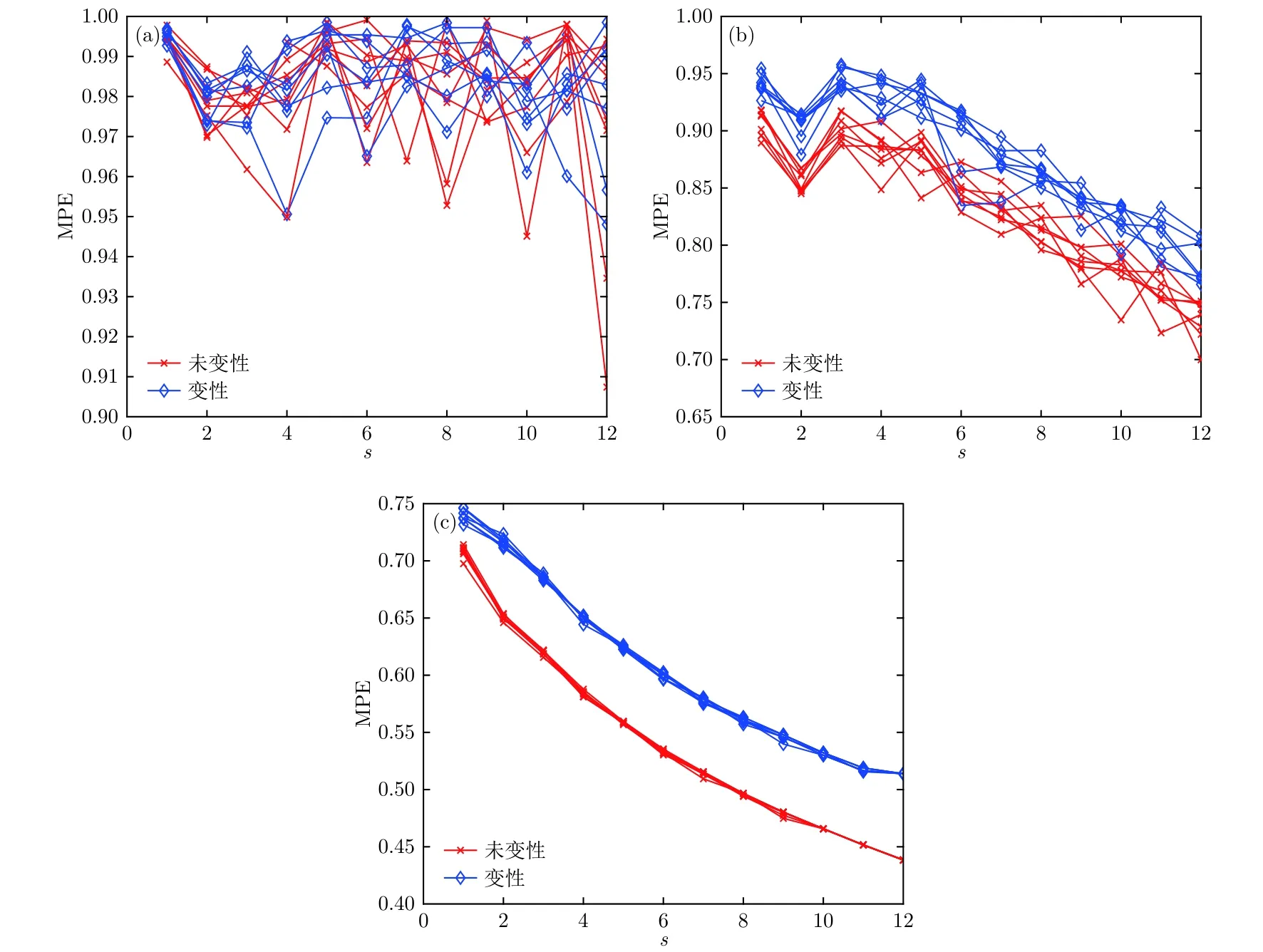
圖4 不同嵌入維數時變性與未變性情況的MPE分布 (a) m= 3; (b) m= 5; (c) m= 7Fig.4. MPE distribution of denatured and undenatured cases with different embedding dimension: (a) m= 3; (b) m= 5; (c) m= 7.

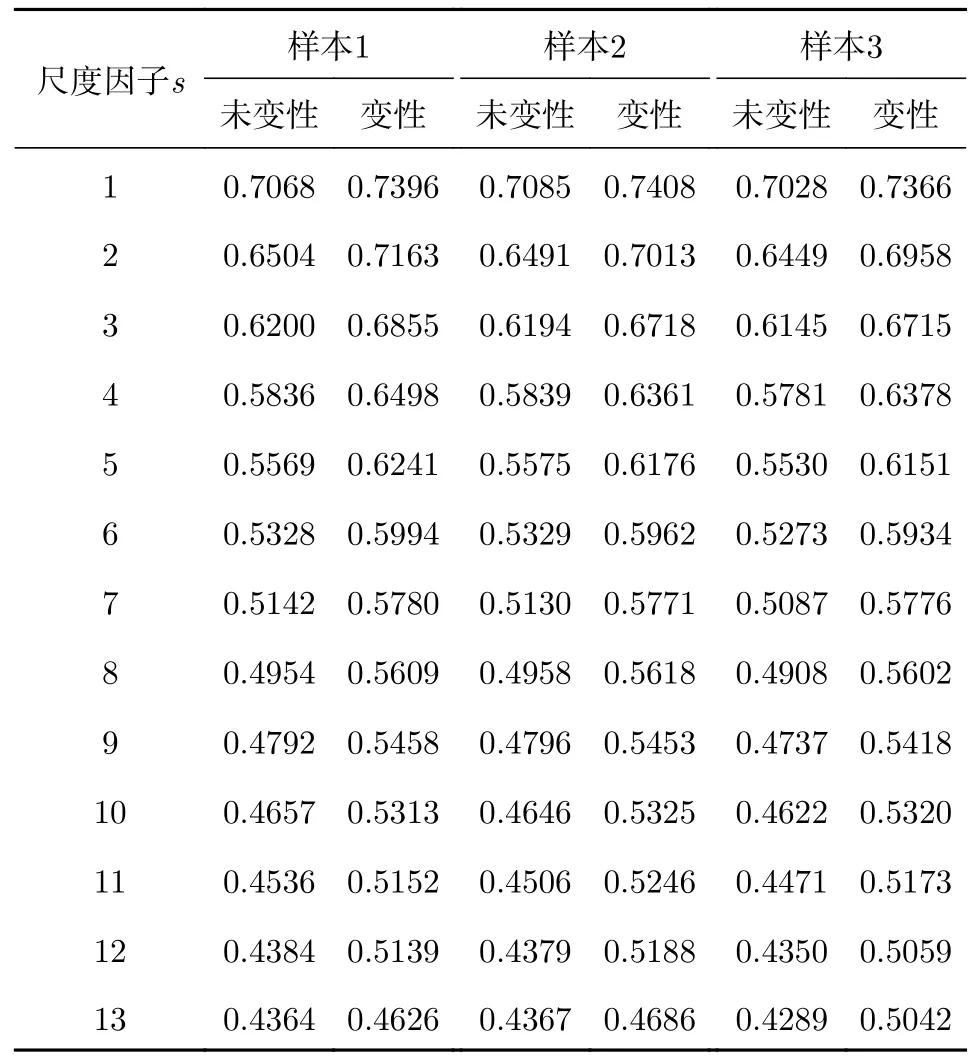
表1 三組樣本在嵌入維數m= 7時各尺度下排列熵平均值Table 1. The average entropy of the three samples at each scale when the embedding dimension m= 7.

由表1可見, 嵌入維數為7時, 尺度因子改變,同一樣本的MPE值發生變化; 尺度因子越大,MPE值越小, 且在不同尺度因子下, 變性組織的MPE值均高于未變性組織的MPE值. 另外, 尺度因子為12時, 第一組樣本與第二組樣本變性狀態與未變性狀態的MPE平均熵值差別較大, 與本文尺度因子參數優化結果相符合; 三組樣本的MPE值隨尺度因子的變化趨勢類似. 后續研究中,延遲時間τ為2, 嵌入維數m取為7, 綜合考慮優化結果選取尺度因子s為12. 通過以上分析可以發現, MPE特征可以作為識別生物組織是否變性的一個重要特征參數.

3.3 GK聚類與生物組織變性識別

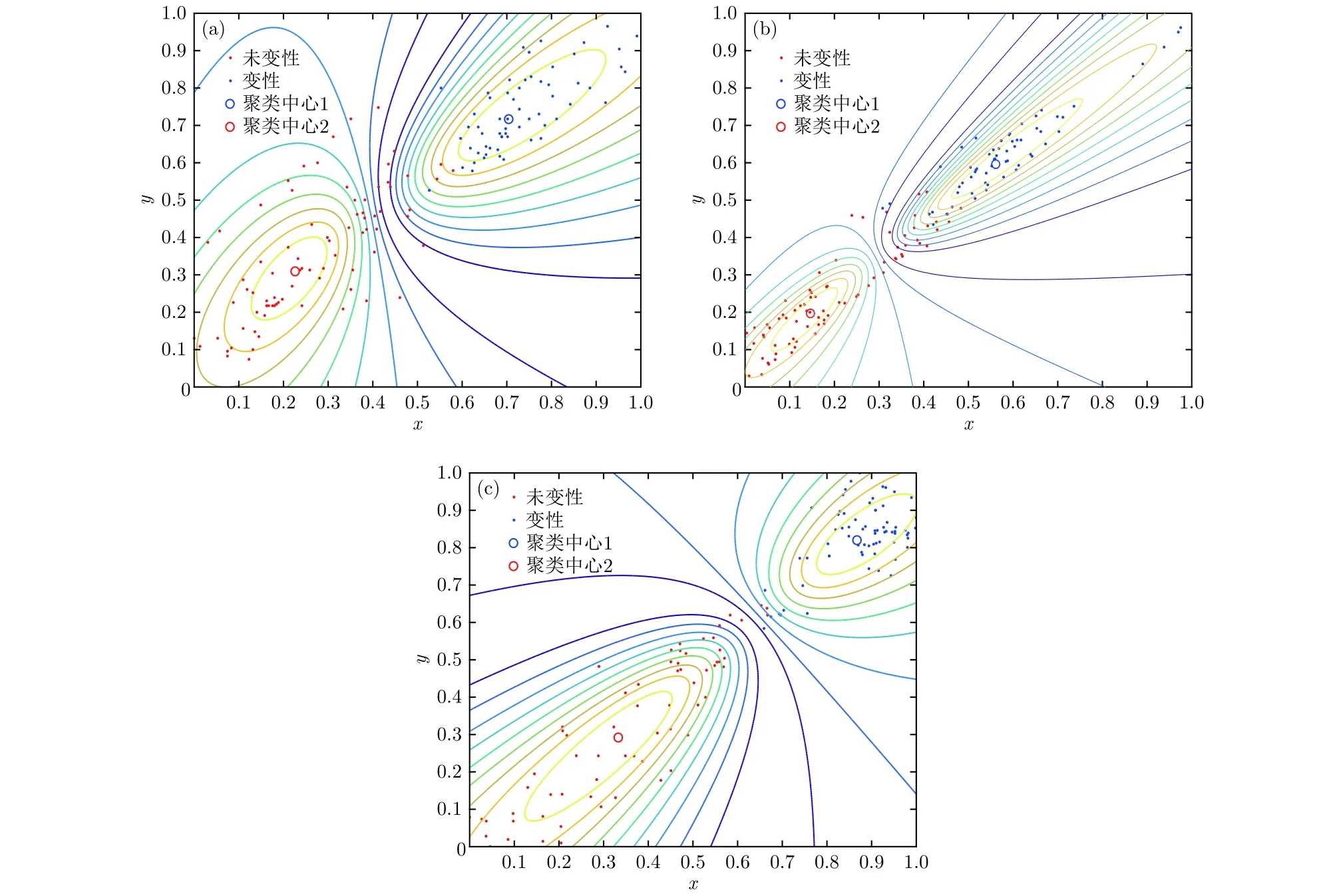
圖5 不同聚類方法對未變性與變性生物組織超聲散射回波信號的聚類效果 (a) EMD-MPE-GK; (b) VMD-WE-GK;(c) VMD-MPE-GKFig.5. Clustering effect on ultrasonic scattering echo signals of undenatured and denatured biological tissues through different clustering methods: (a) EMD-MPE-GK; (b) VMD-WE-GK; (c) VMD-MPE-GK.

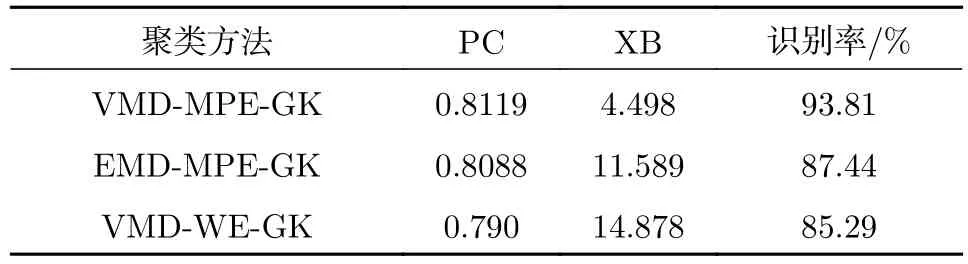
表2 變性與未變性組織識別結果Table 2. Recognition results of denatured and undenatured tissues.

取超聲散射回波信號的重構后信號293例數據, 構成20組樣本. 隨機選取其中150例數據(共10組樣本)作為已知樣本, 后143例數據(10組樣本)作為待識別樣本, 選取各自的參數優化后的MPE值作為特征參量. 提取的特征向量經過GK模糊聚類算法處理后, 結合擇近原則計算歐氏貼近度, 從而實現生物組織變性的模式識別. 為進一步驗證所提方法的有效性, 分別采用EMD-MPE方法以及文獻[8]報道的WE分析(VMD-WE)方法提取特征參量, 最后采用GK模糊聚類對生物組織變性分類識別, 圖5分別為利用EMD-MPE,VMD-WE和VMD-MPE提取組織超聲散射回波信號多尺度排列熵的特征向量、經GK模糊聚類后的二維空間分布以及二維等高線. 計算可得出各種方法的聚類PC, XB以及變性識別率, 識別結果見表2. 由圖5可以看出, 帶有組織變性與未變性特征的超聲散射回波信號經本文方法處理后, 多尺度排列熵特征參量按照變性與未變性基本分布在2個聚類中心的周圍, 并且不同類型之間區分較為明顯, 相較于EMD-MPE-GK聚類和VMD-WEGK聚類方法, 本文方法變性與未變性特征二維空間交疊區域數據點更少, 而且隸屬度等高線區分變性組織與未變性組織的誤識別數據點更少, 類內變性MPE特征更緊密, 分類效果更理想, 這說明基于VMD, MPE和GK模糊聚類的算法對生物組織是否變性具有較好的分類識別效果.

由表2可知, 對比VMD-MPE-GK聚類方法與EMD-MPE-GK聚類方法的識別結果, VMD分解重構信號的XB更小, PC與變性識別率高于EMD分解重構信號; 對比VMD-MPE-GK聚類方法與VMD-WE-GK聚類方法的識別結果, MPE的聚類效果優于WE, 且變性識別率更高. 基于VMD, MPE和GK模糊聚類的生物組織變性識別方法能夠較準確地識別生物組織是否變性, 變性識別率高達93.81%, 且本文所提方法相較于EMDMPE-GK聚類和VMD-WE-GK聚類方法, PC系數更接近1, XB指數更小, 從而證明了所提方法對生物組織變性識別分類的優越性.

4 結 論

本文針對HIFU治療中超聲散射回波信號的特點, 利用VMD與MPE對生物組織變性識別進行了研究, 得出以下結論.

1) VMD能夠有效分解出包含生物組織變性信息的超聲散射回波信號模態分量; 利用參數優化后的多尺度排列熵對重構后的超聲散射回波信號進行特征提取, 結果表明, 選取延遲時間為2, 嵌入維數為7, 尺度因子為12時, 變性生物組織超聲散射回波信號的多尺度排列熵值要高于未變性生物組織的熵值, 多尺度排列熵可以較好地區分未變性組織和變性組織.

2) 利用多尺度排列熵對VMD去噪后超聲信號進行特征提取, 并結合GK模糊聚類和歐氏貼近度進行變性識別; 與EMD-MPE-GK聚類和VMDWE-GK聚類方法相比, 本文方法的聚類效果和變性識別率結果證明了所提方法的分類性能更好, 變性識別率更高, 可用于HIFU治療中生物組織變性識別.