基于二維聲子晶體的大尺寸夾心式換能器的優化設計*

王莎 林書玉

(陜西師范大學, 陜西省超聲學重點實驗室, 西安 710119)

(2018 年11 月2日收到; 2018 年12 月2日收到修改稿)

夾心式換能器應用極為廣泛, 但當其橫向尺寸過大時, 存在耦合振動, 影響其輻射面的位移分布. 本文通過在大尺寸夾心式換能器的前蓋板中加工周期排列的槽, 來形成一種二維聲子晶體結構. 隨后, 采用有限元法對基于二維聲子晶體的大尺寸夾心式換能器的振動傳輸特性、共振頻率以及發射電壓響應進行仿真模擬,討論了開槽高度和開槽寬度對其帶隙、共振與反共振頻率、帶寬以及輻射面位移分布的影響. 研究結果表明,通過在大尺寸夾心式換能器中應用聲子晶體結構可對其進行優化設計. 當大尺寸夾心式換能器的工作頻率位于其帶隙范圍內時, 二維聲子晶體結構能有效地抑制其橫向振動, 從而改善換能器輻射面位移分布的均勻程度. 此外, 在大尺寸夾心式換能器的前蓋板中加工二維聲子晶體結構, 能有效提升換能器的帶寬, 進而拓寬大尺寸夾心式換能器的工作頻帶.

1 引 言

在功率超聲以及水聲領域中, 夾心式換能器(又稱為朗之萬型換能器)的應用極為廣泛, 其主要組成部分為前后金屬蓋板、壓電陶瓷晶堆、金屬電極和預應力螺栓[1-3]. 在設計夾心式換能器時, 通常要求其橫向尺寸小于1/4波長, 以便滿足一維縱向振動理論的要求[4-7]. 但隨著夾心式換能器應用范圍的擴大, 在某些大功率、高聲強的超聲應用中,例如超聲冷拔金屬管、超聲焊接等, 需要增大其橫向尺寸[8,9]. 當大尺寸夾心式換能器處于工作狀態時, 由于材料的泊松效應, 考慮到其縱向振動與橫向振動的耦合, 長度與直徑的縱橫比決定其共振頻率和振動位移分布, 導致換能器輻射面的振動位移分布不均勻, 因此如何抑制橫向振動對大尺寸夾心式換能器的研究具有重要的意義.

Kushwaha等[10]在研究鎳/鋁二維固體周期復合介質時, 首次明確提出了聲子晶體的概念. 聲子晶體是一種具有周期性結構的功能材料, 當彈性波穿過聲子晶體時, 受材料周期性排列結構特點的影響, 某些頻率的波在周期結構中不能傳播, 進而產生帶隙[11-13]. 聲子晶體獨特的振動帶隙特性使其在帶隙范圍內的振動可以被禁止傳播(無限周期結構)或被抑制(有限周期結構)[14,15]. 這一特性使得其在抑制振動領域具有廣泛的應用. 例如, Ronda等[16]和Aragón等[17]在諧振器中應用聲子晶體來抑制橫向振動; Wen等[18,19]將聲子晶體應用于直梁結構以抑制彎曲振動; Zhao等[20]則提出基于聲子晶體的管道結構的減振機制, 并表明聲子晶體結構可以有效減少管道振動.

基于二維聲子晶體結構的帶隙理論, 本文設計了一種新型的基于二維聲子晶體的大尺寸夾心式換能器, 通過在大尺寸前蓋板上加工周期排列的槽來形成二維聲子晶體. 由于周期性的槽沿徑向形成, 使得徑向波無法傳播, 進而有效抑制橫向振動,改善換能器輻射面縱向振動位移分布. 此外, 周期排列的槽結構對大尺寸夾心式換能器的帶寬有一定的影響, 可拓寬其工作頻帶.

2 基于二維聲子晶體的大尺寸夾心式換能器的帶隙分析

傳統的大尺寸夾心式換能器主要由圓柱形后蓋板、壓電陶瓷晶堆和喇叭形前蓋板組成, 其示意圖如圖1(a)所示, 當其處于工作狀態時, 由于其過大的橫向尺寸, 存在強烈的耦合振動, 導致其輻射面的位移分布不均勻. 為此, 我們設計了一種新型的基于二維聲子晶體的大尺寸夾心式換能器, 如圖1(b)所示, 通過在喇叭形前蓋板上沿半徑方向加工周期排列穿透式的槽, 來形成二維聲子晶體結構, 進而有效地抑制橫向振動, 其開槽方式如圖1(b)插圖所示. 本研究中, 我們所設計的槽與槽之間的間隔角度為60°.

圖1 大尺寸夾心式換能器示意圖 (a)未開槽; (b)開槽, 插圖為開槽方式示意圖Fig.1. Schematic diagram of a large-size sandwich transducer: (a) Not grooved; (b) grooved. Inset is a schematic diagram of the grooved method.

為了分析大尺寸夾心式換能器的共振頻率, 在有限元軟件COMSOL Multiphysics的固體力學模塊中建立大尺寸夾心式換能器的模型, 其中圓柱形后蓋板的半徑和高度分別為26 mm和50 mm,選取Steel AISI 4340作為后蓋板材料, 壓電陶瓷晶堆的半徑和高度分別為25 mm和6 mm, 數量為2, 材料為PZT-4, 喇叭形前蓋板的上底面半徑、下底面半徑和高度分別為26, 55和50 mm, 選取Aluminum 6063-T83作為前蓋板材料. 通過計算得到圖1(a)換能器的振型圖, 如圖2所示.

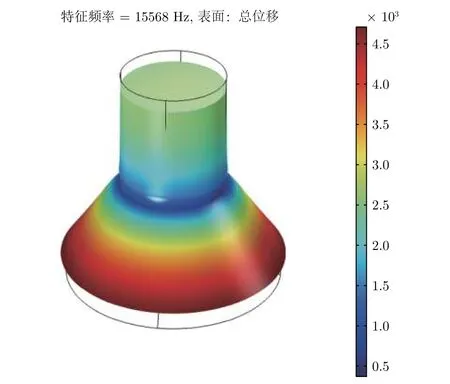
圖2 大尺寸夾心式換能器振型圖Fig.2. Large-size sandwich transducer vibration diagram.

圖2給出了大尺寸夾心式換能器的振型圖. 通過觀察振型圖, 可以發現其共振頻率為15568 Hz.因此, 本文分析換能器前蓋板的帶隙時, 可以選擇性地分析15 kHz附近的帶隙.

在實際情況下的聲子晶體皆為有限周期性結構, 該結構僅對帶隙頻率范圍內的振動傳播起到明顯的抑制作用. 可根據振動傳遞特性曲線, 來確定振動帶隙是否存在以及帶隙的位置和寬度. 本文利用有限元分析軟件COMSOL Multiphysics 模擬了具有有限周期結構的基于二維聲子晶體夾心式換能器的振動傳遞特性.

首先, 在COMSOL Multiphysics中建立6個換能器的模型, 分別為: 當槽寬為8 mm時, 改變槽高, 所設計槽高依次為10, 15, 20和25 mm; 當槽高為20 mm時, 改變槽寬, 所設計槽寬依次為6,8和10 mm. 隨后, 對二維聲子晶體的振動傳輸特性進行模擬仿真. 在有限周期的二維聲子晶體一側沿半徑方向均勻地加上1 m/s2的加速度激勵, 使得振動在二維聲子晶體中傳播, 計算另一側的輸出響應, 可以得到該有限周期二維聲子晶體的振動傳輸特性曲線. 通過計算, 得到基于不同開槽高度和寬度的二維聲子晶體換能器的振動傳遞特性曲線.最后, 經對比分析, 得出開槽高度及寬度對二維聲子晶體帶隙的影響情況, 如圖3所示.

圖3中給出了具有不同開槽尺寸的夾心式換能器的振動傳輸特性曲線. 將振動傳輸率小于1確定為振動傳輸衰減頻率范圍的標準, 從圖3可以看出, 開槽高度及寬度的變化對二維聲子晶體的帶隙有很大的影響. 根據帶隙的定義, 在所考慮的頻率范圍內存在許多方向帶隙. 由此可以在任何帶隙處設計換能器的工作頻率, 并保證其可有效地抑制相應的橫向振動. 考慮到該大尺寸夾心式換能器的共振頻率在15 kHz附近, 故選擇性地分析該頻率附近的帶隙. 不同開槽高度和寬度的大尺寸夾心式換能器的帶隙范圍如表1所列.

圖3 大尺寸夾心式換能器的振動傳輸特性曲線 (a)改變槽高; (b)改變槽寬Fig.3. Vibration transmission characteristic curves of large-size sandwich transducer: (a) Change the groove height; (b) change the groove width.

表1 大尺寸夾心式換能器的帶隙分布情況Table 1. Band gap distribution of large-size sandwich transducers.

從表1中可以看出, 在15 kHz附近, 具有不同槽高及槽寬的換能器均存在方向帶隙, 并且隨著高度的增加, 帶隙向低頻方向移動, 帶隙的寬度減小, 但衰減幅值增大. 同樣地, 隨著開槽寬度的增加, 帶隙對應的頻率有所減小, 其衰減幅值變大.

3 開槽對換能器性能參數的影響分析

本文利用COMSOL Multiphysics模擬大尺寸夾心式換能器的振動特性, 雖然預應力螺栓對換能器有一定影響, 但為了簡化模型, 暫不考慮預應力螺栓的影響. 根據尺寸以及開槽方式的不同, 在COMSOL Multiphysics中建立7個模型, 分別對應未開槽、相同槽寬(8 mm)下不同開槽高度(10, 15,20和25 mm)以及相同槽高(20 mm)不同開槽寬度(6, 8和10 mm). 通過計算, 得到如圖4所示的大尺寸夾心式換能器的共振及反共振頻率.

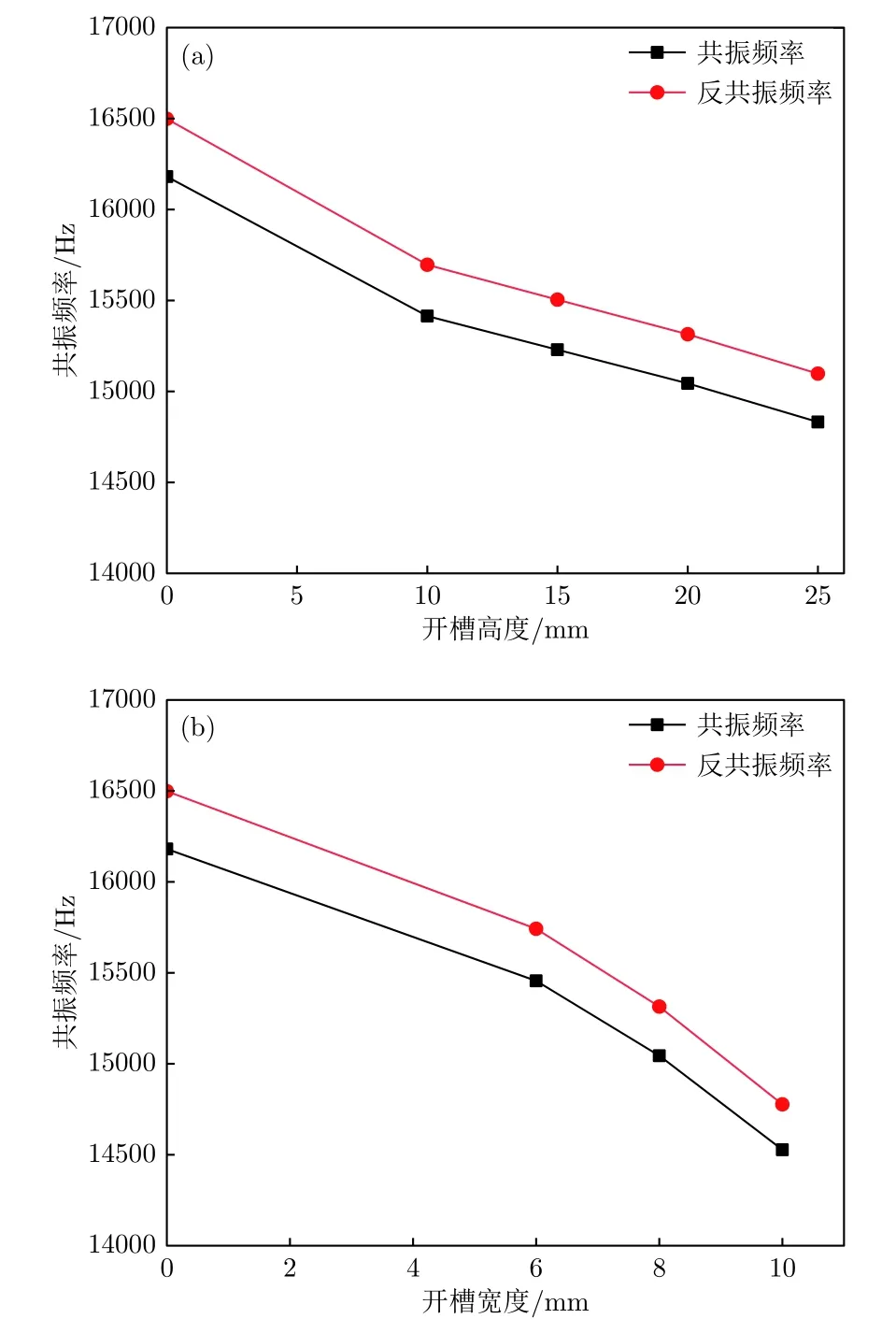
圖4 大尺寸夾心式換能器的共振及反共振頻率 (a)改變槽高; (b)改變槽寬Fig.4. Resonance and anti-resonance frequency of a largesize sandwich transducer: (a) Change the groove height;(b) change the groove width.

本研究發現通過在前蓋板上加工周期性排列的槽, 對換能器的機械性能產生了一定的影響, 換能器的共振頻率與反共振頻率有了相應的變化. 開槽寬度一定, 隨著開槽高度增加, 換能器的共振以及反共振頻率都有相應的減少, 如圖4(a)所示. 同樣地, 開槽高度一定, 隨著開槽寬度的增加, 換能器的共振以及反共振頻率也都有相應的減少, 如圖4(b)所示. 通過對比大尺寸夾心式換能器的共振頻率及其帶隙范圍發現, 開槽后換能器的共振頻率均在其帶隙范圍內, 說明當換能器處于工作狀態時, 聲子晶體結構可以對其橫向振動有抑制作用.

為了分析大尺寸夾心式換能器的帶寬, 通過發射電壓響應曲線來計算其帶寬. 換能器的發射電壓響應是指換能器在某頻率下, 在指定方向上的遠場中, 離換能器等效聲中心1 m處的聲壓值與加到輸入端的電壓的比值. 采用有限元法, 在COMSOL Multiphysics中建立與上述相同的7個模型, 選用水作為負載, 求得基于二維聲子晶體的大尺寸夾心式換能器的發射電壓響應曲線. 圖5給出了換能器的發射電壓響應曲線示意圖, 根據帶寬的定義, 發射電壓響應下降3 dB時, 兩頻率之差為頻帶寬度,即 Δf=f2-f1. 由此可以計算其帶寬, 得到如圖6所示的大尺寸夾心式換能器的帶寬.

圖5 換能器的發射電壓響應曲線示意圖Fig.5. Schematic diagram of the emission voltage response curve of the transducer.

圖6給出了大尺寸夾心式換能器的帶寬. 在大尺寸夾心式換能器的前蓋板上加工周期排列的槽結構, 對其帶寬有一定的影響. 當開槽寬度一定,改變槽高的換能器帶寬如圖6(a)所示, 可以發現隨著開槽高度的增加, 換能器的帶寬不斷增大. 當開槽高度一定, 隨著開槽寬度的增加, 換能器的帶寬也不斷地增大, 如圖6(b)所示. 說明在大尺寸夾心式換能器的前蓋板上加工聲子晶體結構可有效拓寬換能器的工作頻帶.

圖6 大尺寸夾心式換能器的帶寬 (a)改變槽高; (b)改變槽寬Fig.6. Bandwidth of a large-size sandwich transducer:(a) Change the groove height; (b) change the groove width.

在計算換能器的振動特性后, 為了清楚地分析其前蓋板的輻射面的位移分布, 在其端面處, 定義一條沿x軸正方向的截線(ab), 如圖7所示. 采用有限元法, 分別計算出上述7個換能器在其工作頻率下ab線上的縱向位移分布, 如圖8所示.

圖7 大尺寸夾心式換能器輻射面截線示意圖Fig.7. Schematic diagram of the radiation surface section of the large-size sandwich transducer.

圖8中給出了大尺寸夾心式換能器的端面位移分布情況, 可以看出, 與未開槽相比, 開槽后換能器的端面的位移分布更加均勻, 并且開槽寬度以及高度的改變, 對大尺寸換能器端面的位移分布具有一定的影響. 當開槽寬度一定時, 改變開槽高度,隨著高度的增加, 前蓋板輻射面的位移分布更加均勻, 但當高度過大時, 端面的中心位置容易出現強烈的振幅, 如圖8(a)所示. 同樣地, 對于開槽寬度過大的換能器同樣出現了該現象, 如圖8(b)所示.通過對比不同開槽高度及寬度的帶隙與共振頻率,開槽高度和寬度分別為20 mm和8 mm的大尺寸夾心式換能器的共振頻率在帶隙處的衰減程度最大, 故輻射面的位移分布最為均勻. 當基于二維聲子晶體的大尺寸夾心式換能器的工作頻率在其方向帶隙范圍內時, 該方向上彈性波的傳播會受到一定的抑制. 這說明在大尺寸夾心式換能器前蓋板上加工槽, 形成二維聲子晶體, 能有效地抑制其橫向振動, 從而使其輻射面的位移分布更加均勻. 本研究表明, 將聲子晶體結構應用于大尺寸夾心式換能器中, 可顯著提升換能器性能, 為實現大尺寸夾心式換能器的優化設計提供理論支撐.

由于二維聲子晶體的結構能抑制大尺寸前蓋板的橫向振動, 從而均勻其輻射面的位移分布, 同時對共振與反共振頻率以及帶寬都有一定的影響,能有效提升大尺寸夾心式換能器的性能及工作帶寬. 本研究通過在前蓋板上加工二維聲子晶體結構, 最終實現了對大尺寸夾心式換能器的優化設計.

圖8 大尺寸夾心式換能器的端面位移分布 (a)改變槽高; (b)改變槽寬Fig.8. End face displacement distribution of large-size sandwich transducer: (a) Change the groove height;(b) change the groove width.

4 結 論

對基于二維聲子晶體的大尺寸夾心式換能器進行了研究. 利用前蓋板上加工槽的方式形成二維聲子晶體, 使其橫向耦合振動得到有效的抑制, 從而使得縱向的振動模態更加單一. 分別討論了開槽高度和開槽寬度對大尺寸夾心式換能器的帶隙、共振與反共振頻率、帶寬以及輻射面的位移分布的影響, 得出以下結論.

1) 基于二維聲子晶體的大尺寸夾心式換能器存在橫向帶隙.

2) 在開槽寬度一定時, 基于二維聲子晶體的大尺寸夾心式換能器的帶寬隨著開槽高度的增加而增大. 同樣地, 在開槽高度一定時, 基于二維聲子晶體的大尺寸夾心式換能器的帶寬隨開槽寬度的增加而增加.

3) 將二維聲子晶體結構應用于大尺寸夾心式換能器前蓋板中, 能有效地抑制橫向振動, 均勻前蓋板輻射面的位移分布.

總之, 二維聲子晶體結構應用于大尺寸夾心式換能器中, 能有效地抑制換能器的橫向振動, 并拓寬換能器的工作頻帶, 可以對大尺寸夾心式換能器的性能進行優化設計.