箔片安裝位置對氣體軸承性能影響的仿真分析

李昊,耿海鵬,孫巖樺,唐思訓,齊壘,虞烈

(西安交通大學機械結構強度與振動國家重點實驗室,710049,西安)

對轉子系統進行準確的性能仿真預測已經成為現代旋轉機械的設計趨勢[1]。彈性箔片動壓氣體軸承是一種柔性表面支承軸承。相比傳統油潤滑軸承,彈性箔片動壓氣體軸承避免了高溫工況導致的潤滑工質惡化,同時,可以省略復雜的供油系統,使系統結構布局更加緊湊[2]。20世紀70年代以來,隨著航空航天、核動力、制冷工程技術等對設備要求的不斷提高,彈性箔片動壓氣體軸承得到了廣泛的應用,同時學術界對箔片軸承的研究也不斷深入[3]。

與滾動軸承及油潤滑軸承相比,彈性箔片動壓氣體軸承由于氣體介質黏度低,導致軸承承載力較低,剛度、阻尼偏小,而這對于轉子系統整體的穩定性不利[4]。因此,自從彈性箔片動壓氣體軸承的概念誕生以來,學者們提出了多種結構形式用于提高軸承性能。美國Honeywell公司提出了多葉型箔片軸承,并首次進行試驗驗證[2]。此后,多懸臂箔片軸承[5]、波箔型箔片軸承[6]、多層波箔型箔片軸承[7]、平箔型箔片軸承[8]、多層鼓泡箔片軸承[9]、壓縮彈簧箔片軸承[10]、金屬橡膠箔片軸承[11]、稀薄氣體潤滑軸承[12]等的相關研究相繼展開,試驗結果表明,這些新結構的彈性箔片動壓氣體軸承分別擁有提高軸承承載力、改善動態特性、增強穩定性等優點。

在彈性箔片動壓氣體軸承的箔片周向定位方式上,通常采用點焊或狹槽固定。點焊工藝簡單,對軸承座要求低,但在實際運行中,頂層箔片會隨著啟停次數增多及工作時間的增長發生磨損,底層拱箔會發生松弛甚至壓潰,而狹槽固定的安裝形式便于更換箔片,因此應用更加廣泛[13]。

在彈性箔片動壓氣體軸承系統試驗時,頂層箔片安裝狹槽通常布置在軸承座頂部,與轉子重力方向相反[14],但并沒有相關文獻指出這樣布置的原因,同時也沒有文獻指出不同的布置形式會造成什么樣的結果。因此,本文將研究頂層箔片安裝狹槽的位置對彈性箔片動壓氣體軸承性能的影響,通過計算分析,得到箔片的安裝策略。

1 理論分析

1.1 箔片開口狹槽位置模型

圖1為進行理論分析與性能測試時常見的彈性箔片動壓氣體軸承安裝形式,主要由軸承座、頂層箔片和底層拱箔組成[15]。分析可知:頂層箔片通過軸承座上的狹槽實現固定,與軸頸表面形成摩擦副;由于軸頸與軸承間存在偏心距e及偏位角ψ,所以軸頸在以角速度ω旋轉的過程中,可以形成動壓氣體潤滑膜,產生的氣膜力與轉子自重W相平衡,實現支承作用;插入狹槽固定的底層拱箔在氣體動壓的作用下產生彈性變形,實現柔性支承效果。在進行彈性箔片動壓氣體軸承裝配時,通常將固定箔片的狹槽置于正上方,即圖中箔片安裝角θ=0°處。

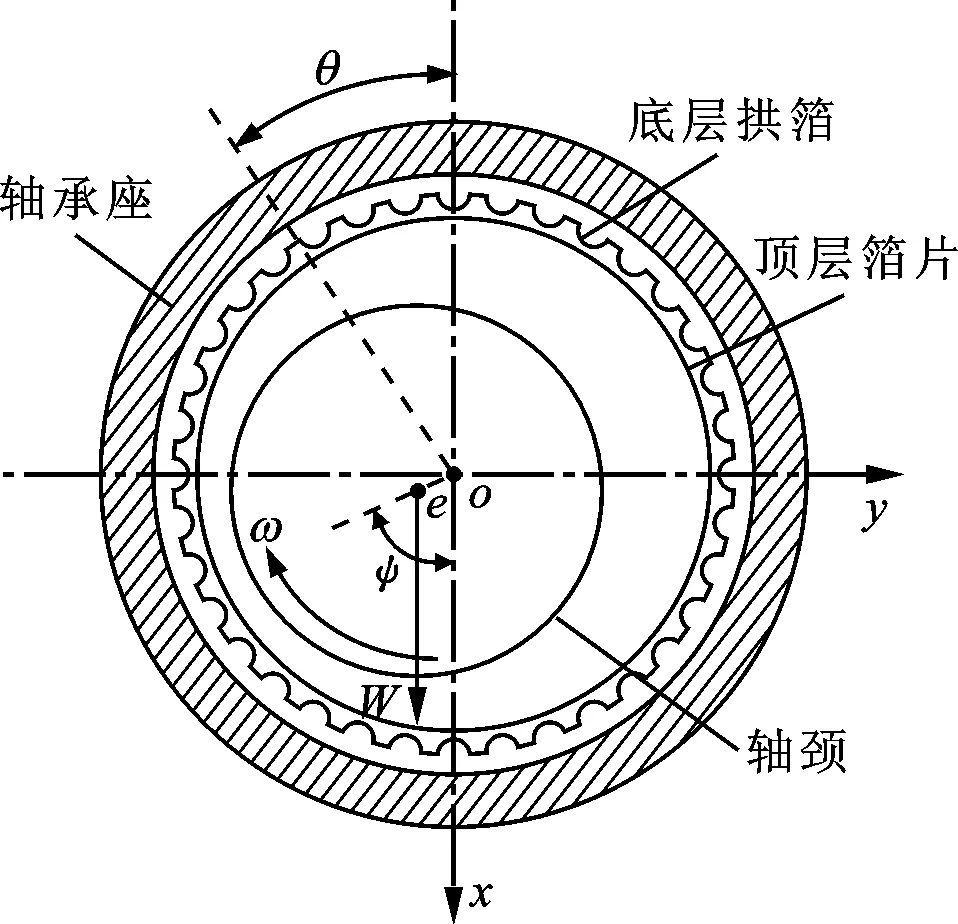
圖1 彈性箔片動壓氣體軸承的安裝形式

1.2 控制方程

對于使用常溫常壓空氣潤滑介質的彈性箔片動壓氣體軸承,其潤滑情況可以使用理想氣體的雷諾方程[15]描述,即

(1)

式中:x和z分別為軸承的周向和軸向長度;h為氣膜厚度;μ為氣體動力學黏度;ρ為氣體密度;p為氣膜壓力;U為軸頸表面旋轉線速度;t為時間。該方程是在廣義雷諾方程的基礎上忽略表面伸縮效應和擠壓效應得到的,這種簡化形式在相關研究中得到了廣泛的應用[16]。

由于氣體具有明顯的可壓縮性,因此氣體軸承中氣膜的密度不能再被視為常量,需要特殊考慮。結合理想氣體狀態方程,可以得到式(1)的量綱一形式為

(2)

歸一化規則為

(3)

式中:R為軸承半徑;φ為量綱一周向坐標;λ為量綱一軸向坐標;Pa為環境壓力,計算中取值為標準大氣壓;P為量綱一氣膜壓力;C為名義氣膜厚度;τ為量綱一時間;H為量綱一氣膜厚度,其描述公式為

H=1+εcos(φ+ψ)+wt

(4)

其中,ε=e/C表示軸頸相對于軸承的偏心率,wt是彈性箔片在氣體動壓效果下發生彈性變形的量綱一形式,其數學描述[16]為

(5)

其中,α為拱箔柔度,l0為波箔半波紋跨度,ν為底層拱箔材料泊松比,s為單位波紋寬度,E為底層拱箔材料彈性模量,tb為底層拱箔材料厚度,S為拱箔量綱一柔度。

2 數值計算

描述箔片軸承壓力分布的方程為非線性方程,無法求出精確的理論解,本文采用有限差分法求解彈性箔片軸承壓力分布,差分格式采用二階中心差分,具體形式不做介紹。給定初始氣膜壓力及厚度,通過迭代求解即可獲得氣膜壓力及厚度的數值解,進而計算箔片軸承承載力等靜態性能。箔片軸承的量綱一承載力計算公式[16]為

(6)

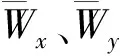
在計算過程中,需要使用箔片彈性變形值不斷修正各節點氣膜厚度,并使用修正后的氣膜厚度進行氣膜壓力計算,如此反復迭代,直到兩次氣膜壓力計算結果滿足收斂要求,其數學描述為

(7)

式中:∑Pi表示第i次迭代所有節點氣膜壓力的代數和;∑Pi-1表示第i-1次迭代所有節點氣膜壓力的代數和;δ表示收斂條件,通常取10-5即可滿足計算精度要求。

(8)

將擾動方程與雷諾方程聯立求解,即可得到箔片軸承的剛度、阻尼系數為

(9)

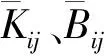
通過上述分析,可以得到箔片軸承的求解流程,如圖2所示。

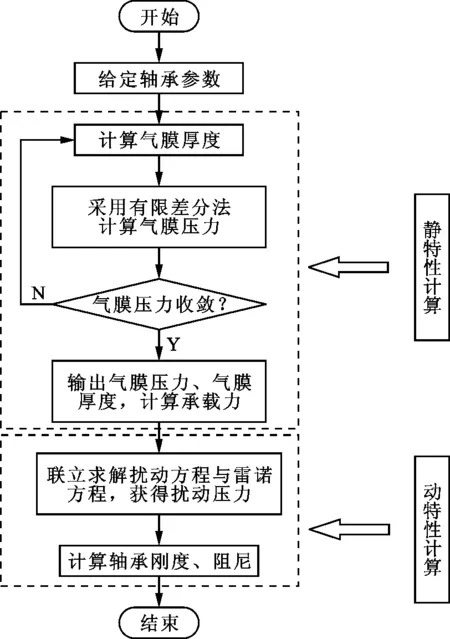
圖2 箔片軸承求解流程圖

3 仿真結果及分析

為驗證本文所述數學模型與計算程序的正確性,使用本文所述模型計算了不考慮箔片安裝位置時的軸承特性,并與已有文獻進行了對比。表1是使用本文所建立求解模型的計算結果與已有文獻給出數據的對比(取寬徑比為2.0,軸承數為1.0),對比結果驗證了本文所建立求解模型的準確性。

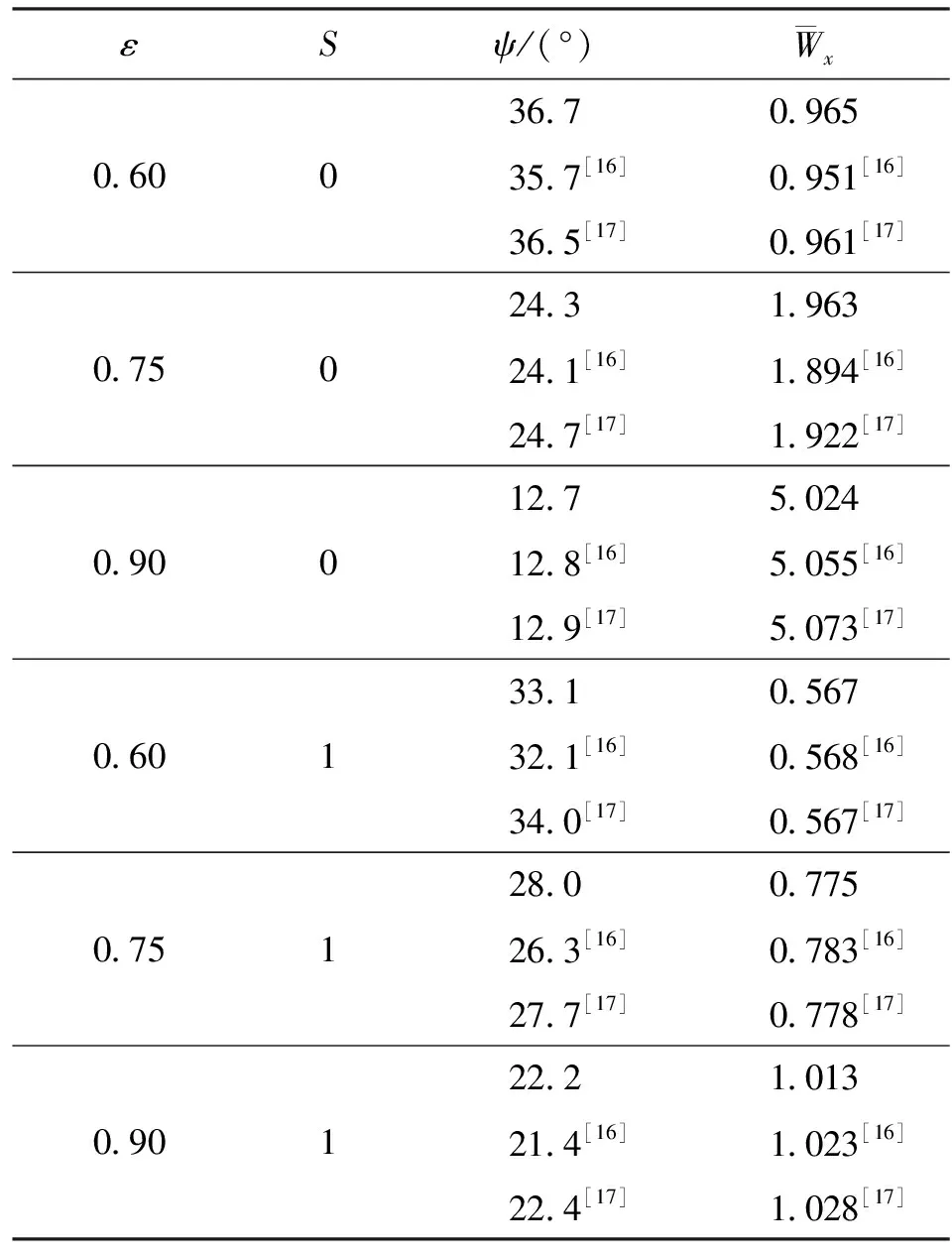
表1 計算結果驗證

表2給出了本文分析所用軸承的結構及工作條件基本參數。為方便進行計算,將箔片沿周向剖開為矩形求解域,剖線為圖1中箔片正上方,即x軸負半軸。同時,對矩形求解域進行網格劃分,周向和軸向的單元數為72×25。

表2 氣體軸承基本參數

3.1 承載力分析

圖3給出了不同偏心率下,箔片軸承承載力與箔片安裝角的關系曲線,可以看出:當狹槽處于某一位置區間時,其具體位置并不會對承載力構成顯著影響,相反,當狹槽位置處于“敏感”位置區間時,會非常顯著地影響軸承承載力,且偏心率越大,影響越顯著;當ε=0.9、θ=170°時,承載力變為最大承載力的32%;當ε=0.3,0.5,0.7,0.9時,對承載力影響最大的箔片安裝角分別為155°、158°、162°、170°,而對應偏心率下偏位角的計算結果分別為56°、44°、23°、13°。由此可見,在大載荷條件下(ε=0.7,ε=0.9),箔片最“敏感”安裝角與360°整周式箔片計算所得的偏位角近似構成了互補關系,其誤差主要是由于本文計算中使用的軸瓦張角為350°。這說明最“敏感”的箔片安裝角位于整周式箔片軸承的壓力峰值區域附近,因此箔片安裝時,安裝狹槽應盡量遠離這一區域。

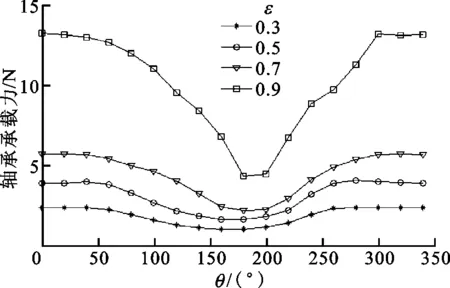
圖3 軸承承載力與箔片安裝角的關系曲線

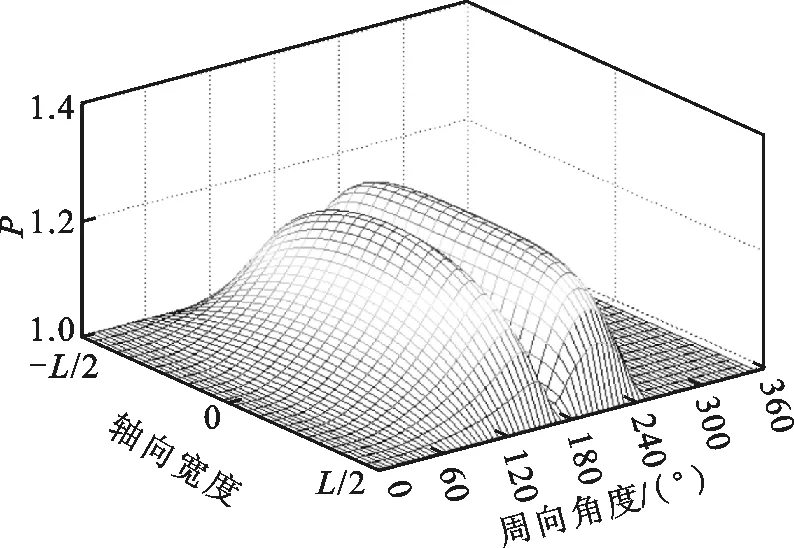
為研究承載力下降的原因,繪制了ε=0.7時,箔片軸承的氣膜厚度與氣膜壓力在不同箔片安裝角下的分布圖,如圖4和圖5所示。從圖4可以看出,箔片安裝處氣膜厚度在數值上遠大于其他位置處,不會形成有效氣膜壓力。因此在計算氣膜壓力時,該段氣膜厚度置空,氣膜壓力置為環境壓力1,如圖5所示。從圖5可以看出:當箔片安裝角處于“敏感”位置區間時,氣膜壓力分布會發生顯著變化,而平均氣膜壓力的下降會導致軸承承載力的下降。這主要是因為箔片安裝位置極大地影響了氣膜厚度的分布,而氣體軸承的壓力分布對氣膜厚度非常敏感。相反,當箔片安裝角遠離“敏感”位置區間時,安裝位置角的具體數值并不會對氣膜厚度及壓力分布構成顯著影響,這也說明,在實際安裝時,只需保證箔片安裝角處于一個位置區間即可,并不需要嚴格規定具體數值。

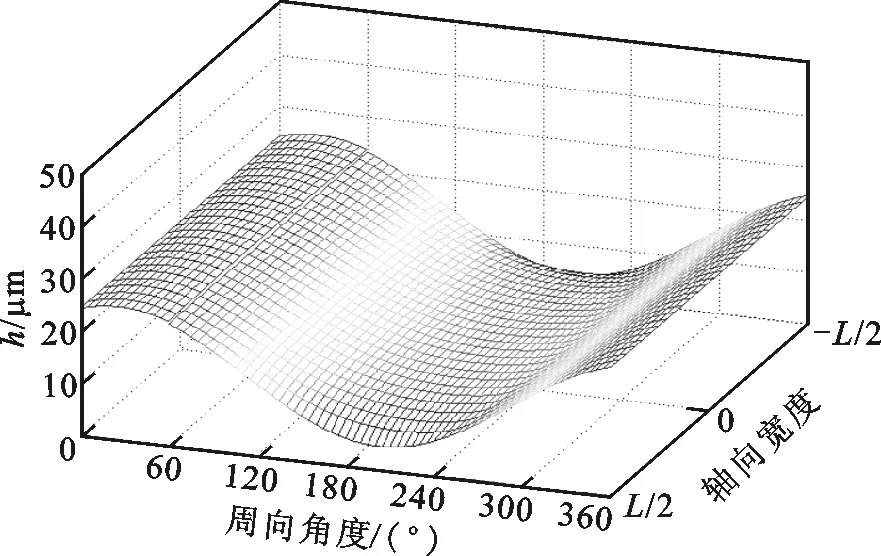
(a)θ=0°

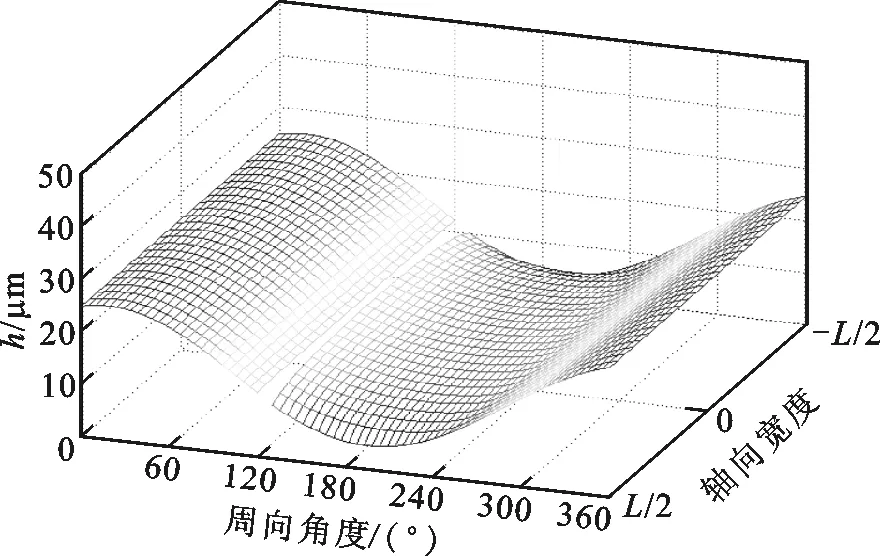
(b)θ=120°

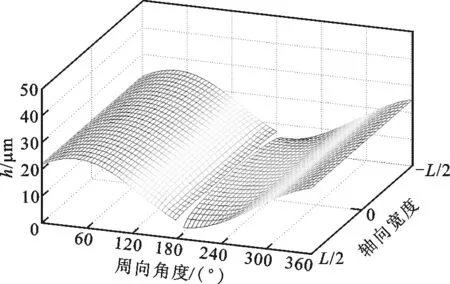
(c)θ=180°

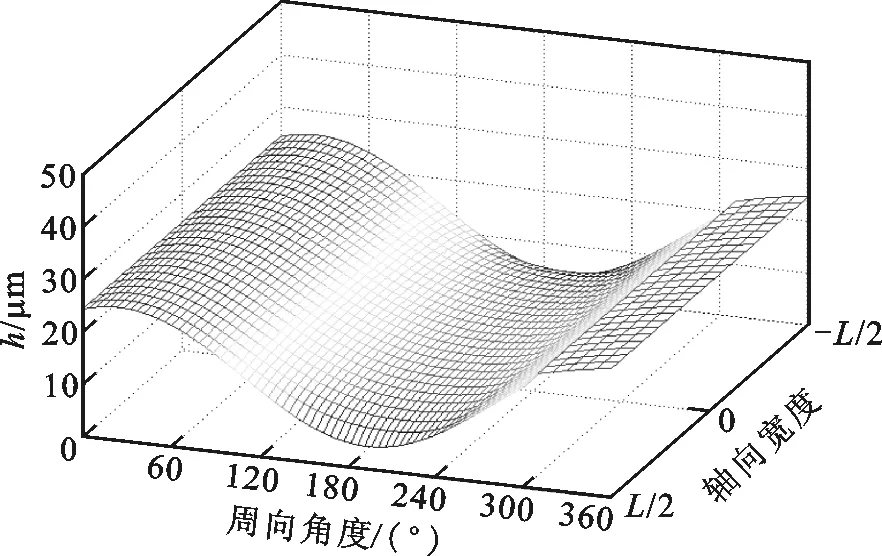
(d)θ=300°圖4 箔片軸承氣膜厚度分布

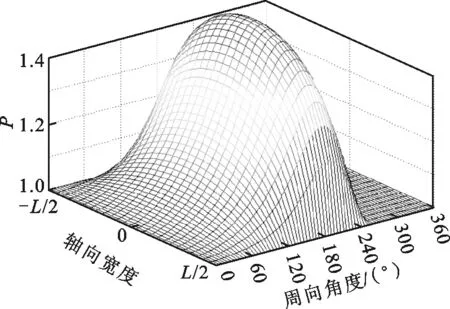
(a)θ=0°

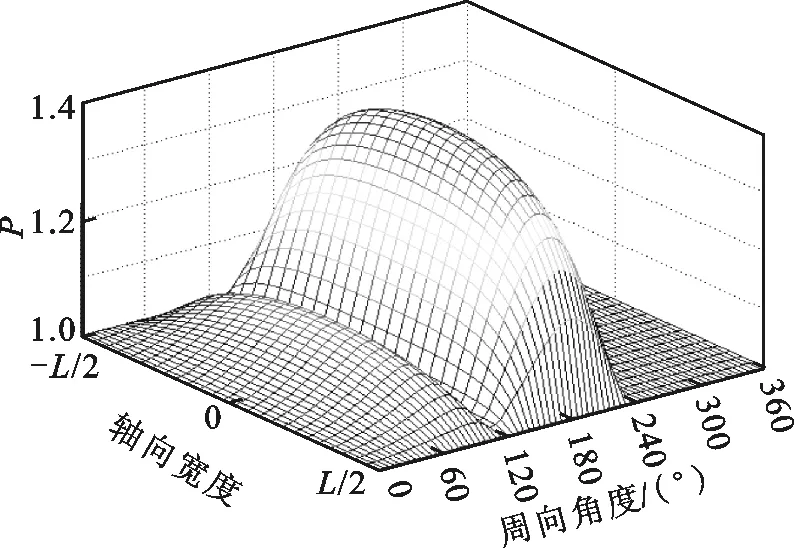
(b)θ=120°

(c)θ=180°

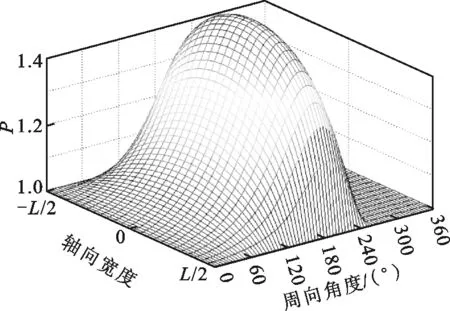
(d)θ=300°圖5 箔片軸承氣膜壓力分布

3.2 動力學特性分析

圖6為ε=0.7時,箔片軸承剛度系數與箔片安裝位置角的關系曲線,分析可知:當狹槽處于“敏感”位置區間時,箔片軸承的主剛度會顯著下降,而交叉剛度會上升,對箔片軸承的穩定工作不利;當狹槽位置處于“敏感”位置區間時,交叉剛度會在數值上非常接近主剛度,意味著軸承的工況已經非常惡劣,微小擾動就可能造成軸承失穩;x方向的最小剛度數值僅為最大剛度的22%,說明箔片的安裝位置會極大的影響箔片軸承的穩定性;剛度系數的“敏感”位置區間相比于承載力的“敏感”位置區間提前了約20°～30°,這主要是因為剛度系數對壓力梯度的變化更為敏感。

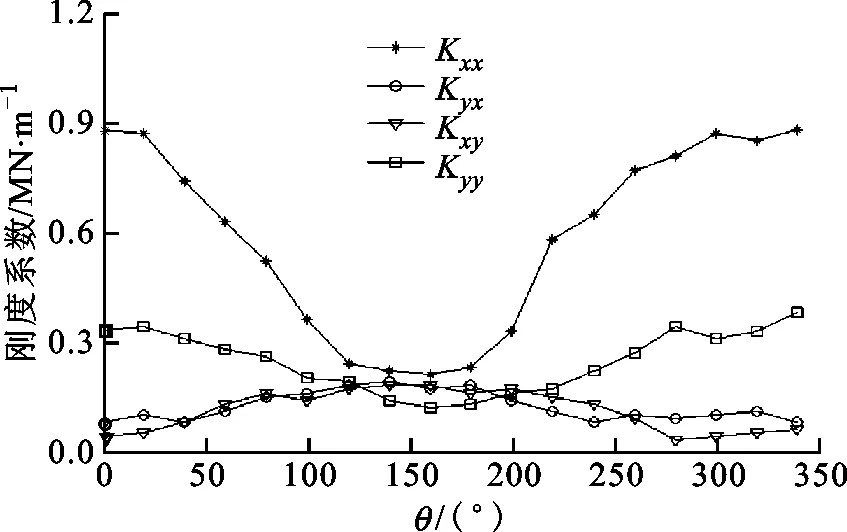
圖6 軸承剛度系數-箔片安裝角曲線

圖7為ε=0.7時,箔片軸承阻尼系數與箔片安裝位置角的關系曲線,可以看出,阻尼系數的變化趨勢與剛度系數類似,所不同的是,阻尼系數的變化相對平緩,特別是兩個方向上的交叉阻尼變化值均非常小。

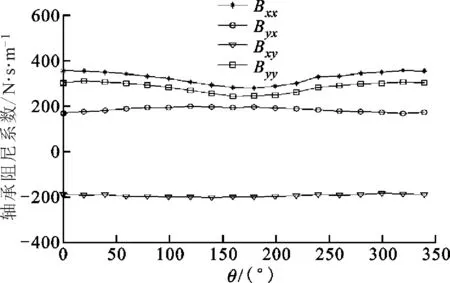
圖7 軸承阻尼系數-箔片安裝角曲線

4 結 論

本文分析了彈性箔片氣體軸承中箔片位置安裝角對軸承靜、動特性的影響,主要結論如下。

(1)箔片軸承的安裝位置角會對軸承承載力構成顯著影響。這主要是由于箔片安裝位置影響了氣膜厚度的分布,氣體動壓效果對氣膜厚度十分敏感,因此造成了承載力的變化;同時,箔片安裝的“敏感”位置區間中承載力最低的安裝角與整周式箔片軸承的偏位角為互補關系。

(2)箔片軸承的安裝位置角對氣膜剛度系數與阻尼系數均有影響,其中對于剛度系數的影響十分顯著,對阻尼系數的影響相對較小。

(3)當箔片安裝角處于“敏感”區間時,箔片軸承的靜、動特性均會發生顯著變化,相反,當箔片安裝角避開“敏感”區間時,箔片軸承的靜、動特性則不會受到明顯影響,說明箔片安裝時,只需要保證安裝角在一定范圍內即可,不需要嚴格規定具體數值。

(4)提出一種箔片軸承安裝策略,首先進行360°整周箔片軸承計算,獲得偏位角,然后將安裝狹槽布置在偏位角的對側,即遠離承載區位置附近可以避免其對氣體軸承動、靜態性能的影響。