自適應誤差四元數無跡卡爾曼濾波四旋翼飛行器姿態解算方法

崔培林,周翟和,呂品,胡斌

(南京航空航天大學自動化學院,211106,南京)

四旋翼飛行器(后文簡稱飛行器)是控制科學和無人機領域內備受關注的研究對象,飛行器姿態信息的測量精度直接影響了飛行器速度、位置的導航精度[1-2]。在小型飛行器中,常使用陀螺儀、加速度計以及磁強計作為姿態測量器件,陀螺儀存在累積誤差,而加速度計和磁強計受外界干擾較大,需要對其進行有效的數據融合以保證獲得較為精確的姿態角[3-4]。

在姿態解算方法中,文獻[5-6]使用卡爾曼濾波(Kalman Filter,KF)算法進行數據融合,該方法建模簡單,實時性較好,但是忽略了非線性因素對濾波帶來的影響。文獻[7-8]使用擴展卡爾曼濾波(Extended Kalman Filter,EKF)方法,這是一種關于噪聲均值和協方差的線性化方法,用這種方法對狀態方程和量測方程進行線性化處理,必然會引入誤差。對于弱非線性,EKF可獲得較為準確的結果,然而,對于強非線性,線性化模型的誤差可能導致濾波器性能下降甚至發散。文獻[9]提出了基于四元數無跡卡爾曼濾波(Unscented Kalman Filter,UKF)算法,該方法使用四元數法進行姿態解算,保證了系統可以全姿態工作,具有很好的非線性姿態估計精度與濾波穩定性,但是具有較大的計算量。文獻[10-11]中提出了誤差四元數卡爾曼濾波(Error Quaternion Kalman Filter,EQKF)方法,使用誤差四元數的方法構建系統的狀態方程與量測方程,具有計算量小,響應快的優點,但是也忽略了非線性因素的影響。

針對慣性傳感器在飛行器姿態解算中存在隨機漂移誤差和易受到非重力加速度影響的問題,本文在以上研究的基礎上,提出了一種自適應誤差四元數無跡卡爾曼濾波(Adaptive Error Quaternion Unscented Kalman Filter,AEQUKF)的飛行器姿態解算方法。選用誤差四元數和陀螺儀的關系,并結合陀螺儀漂移誤差模型構建系統的狀態方程,利用加速度計和磁強計數據構建系統的量測方程,最后選用誤差四元數無跡卡爾曼濾波(Error Quaternion Unscented Kalman Filter,EQUKF)框架實現數據融合,通過判斷系統是否存在非重力加速度,自適應調整量測噪聲協方差矩陣,減小非重力加速度的影響。該方法抑制了傳感器隨機漂移誤差,自適應補償了非重力加速度對姿態估計的影響,相比較EKF算法進一步提高了姿態系統檢測的精度。實驗表明,當飛行器有非重力加速度時,該算法比傳統算法具有更好的姿態解算精度。

1 誤差四元數無跡卡爾曼濾波建模

1.1 狀態方程的建立

陀螺儀輸出的信號與運動條件無關,但是陀螺儀信號具有偏置誤差[12-13]。因此,陀螺儀測量模型為角速度、偏置誤差、白噪聲的總和,即

ωo=ω+εg+ng

(1)

式中:ωo表示陀螺儀的輸出;ω表示實際角速度;εg表示陀螺儀的偏置誤差;ng表示陀螺儀的零均值白噪聲。

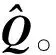
若用?表示四元數乘法,則計算真實四元數的微分方程為

?ω

(2)

計算四元數的估計值的微分方程為

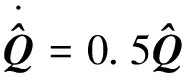
?ωo

(3)

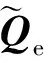
(4)

式中

Qe=[qe1qe2qe3]T

(5)

其中qe1、qe2、qe3為誤差四元數的3個參數。

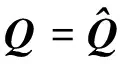
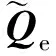
(6)

對式(6)兩邊求導可得

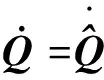
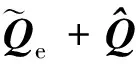
(7)

將式(1)(2)代入式(7)可得

(8)

將式(6)代入式(8)可得

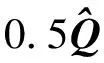
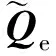
(9)

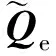
(10)

進一步地,將式(1)代入式(10)可得

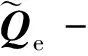
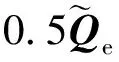
(11)

對于3階向量,定義[p×]為

(12)

因為誤差四元數第一項為常數項1,對其求導為常數0,對后面模型的搭建沒有影響。式(11)可簡化為

0.5(εg+ng)+[Qe×](εg+ng)

(13)

又因為

[Qe×]ωo=-[ωo×]Qe

(14)

而Qe、εg和ng很小,所以[Qe×](εg+ng)為高階小項,可以忽略。將式(14)代入式(13),忽略掉[Qe×]·(εg+ng)可得

(15)

若nεg為陀螺儀漂移零均值白噪聲,則陀螺儀漂移模型為

(16)

選取系統狀態量為

x=[qe1qe2qe3εgxεgyεgz]T

(17)

式中:εgx、εgy、εgz表示陀螺儀漂移三軸分量。

根據式(15)～(17),可得誤差四元數UKF的狀態方程為

xk=f(xk-1)+wk-1

(18)

式中:f(xk-1)為系統的狀態轉換方程;wk-1為系統過程噪聲。f(xk-1)和wk-1的具體公式為

(19)

(20)

式中T表示采樣時間。

系統協方差矩陣為

(21)

式中Qg和Qεg分別為陀螺儀噪聲協方差矩陣和陀螺儀漂移噪聲協方差矩陣,具體值由實驗獲得。

1.2 觀測方程的建立

加速度輸出數據信號模型為重力、非重力加速度、零均值白噪聲的總和,磁強計輸出數據信號模型為地磁場和零均值白噪聲的總和,公式為

(22)

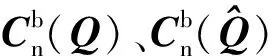
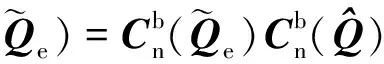
(23)

選取觀測量z=[fafm]T,根據式(18)(19),誤差四元數UKF的量測方程為

zk=h(xk)+vk

(24)

式中:h(xk)為系統的量測轉換方程;vk為系統量測噪聲。h(xk)和vk的具體公式為

(25)

(26)

由于ab和na互不相關,所以量測噪聲協方差矩陣公式為

(27)

式中:Rb為非重力加速度協方差矩陣,具體值參考本文2.2節;Ra和Rm分別為加速度計噪聲協方差矩陣和磁強計噪聲協方差矩陣,具體值由實驗獲得。

2 自適應誤差四元數無跡卡爾曼濾波算法

2.1 對稱采樣

無跡變換(Unscented Transformation,UT)的主要思想是使用近似概率分布來代替非線性函數,在原先狀態分布中按照某一規則選取確定性的點集S(即Sigma點),使這些點集的均值和方差等于原狀態分布的均值和方差。通過非線性變換,加權計算得到變換后的均值和方差。

UT變換算法中采樣策略是關鍵部分,本文的采樣策略為對稱采樣[15],具體如下。

(1)Sigma點的產生

(28)

(2)權值計算

(29)

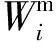
2.2 非重力加速度補償

當飛行器在上升、下降、加速、減速等階段存在著較大的非重力加速度時,加速度計不能將其區分出來,由加速度計解算得到的姿態角度信息將受到非重力加速度的影響,姿態角包含較大誤差,將直接影響飛行器的飛行控制。本文通過自適應調整協方差矩陣來減少非重力加速度帶來的影響。

判斷是否存在非重力加速度的公式為

|‖f‖-g|<δg

(30)

式中:‖f‖為加速度輸出數據的范數;g為重力加速度;δg為閾值常數,其取值和加速度計噪聲有關。

若上式滿足,則飛行器不存在非重力加速度,即

Rb=0

(31)

反之,則存在非重力加速度,即

(32)

式中:ρ為常數,由多次實驗獲得,用于調節濾波精度;ra為加速度計的殘差信息,公式為

ra=zk-h(xk)

(33)

2.3 自適應誤差四元數無跡卡爾曼濾波算法

(34)

(35)

(2)狀態更新。根據對稱采樣策略生成Sigma點,公式為

(36)

計算Sigma點的下一步預測值,對每個Sigma點非線性變換,公式為

χk+1,k=f(χk)

(37)

對變換后的Sigma點進行加權得到下一步預測和協方差矩陣,公式為

(38)

(39)

根據非線性觀測方程對Sigma點集χk進行非線性變換,公式為

zk+1,k=h(χk+1,k)

(40)

使用加權計算,得到預測的觀測值為

(41)

(3)非重力加速度補償。根據式(30)判斷飛行器系統是否存在非重力加速度。當不存在非重力加速度時,加速度輸出的數據為當地重力加速度值,非重力加速度協方差矩陣為式(31),代入本文算法求解姿態數據;當系統存在非重力加速度時,殘差信息式(33)中包含了最新時刻的加速度計數據,也保留了非重力加速度的信息,非重力加速度越大,殘差信息也就越大,相應的非重力加速度協方差矩陣也就越大。利用式(32)調整協方差矩陣Rb,代入本文算法求解姿態數據。非重力加速度協方差矩陣是根據非重力加速度大小自適應更新的,非重力加速度越大,補償效果越明顯。

(4)量測更新。協方差矩陣更新公式[19-20]為

(42)

量測輸出協方差矩陣更新公式為

(43)

卡爾曼增益矩陣更新公式為

(44)

狀態更新后,濾波值更新公式為

(45)

后驗方差矩陣更新公式為

Pk+1=Pk+1,k-Kk+1Pzk+1Kk+1

(46)

3 仿真與實驗驗證

使用Matlab仿真平臺和飛行器平臺對提出的算法進行驗證。算法驗證分為靜態實驗驗證和動態非重力加速度仿真驗證。靜態實驗主要是驗證改進的算法具有良好的濾波效果,可以抑制陀螺漂移,獲得較高的姿態解算的精度。動態非重力加速度仿真主要是為了驗證飛行器在存在非重力加速度的情況下,該方法可以有效地減小非重力加速度影響,獲得更為準確的濾波值。

具體實驗和仿真參數如下:T=0.01 s,Ra=0.000 1I3,Rm=0.000 1I3,Qg=0.000 1I3,Qεg=0.000 001I3,P=0.000 1I6,ρ=10,δg=0.02。

3.1 靜態驗證

利用飛行器平臺進行靜態實驗驗證本文方法。飛行器實驗平臺如圖1所示,姿態測量器件為MPU6050(三軸陀螺儀和三軸加速度計)和HMC5883L(三軸磁強計),飛行器軸長45 cm,數據通過UART通信,將傳感器數據發送到上位機。飛行器在靜止狀態下的俯仰角、航向角和橫滾角均為0°,飛行器不存在非重力加速度。

圖1 飛行器實驗平臺

圖2和表1給出了靜態實驗中AEQUKF的解算結果,圖和表中“加速度計”、“陀螺儀”和“磁強計”表示該類傳感器數據經過四元數解算方法直接解算得到的姿態數據,可以看出:相較于加速度計和磁強計的解算結果,AEQUKF具有較高的姿態解算精度;相較于陀螺儀的解算結果,AEQUKF濾除了陀螺漂移帶來的影響。

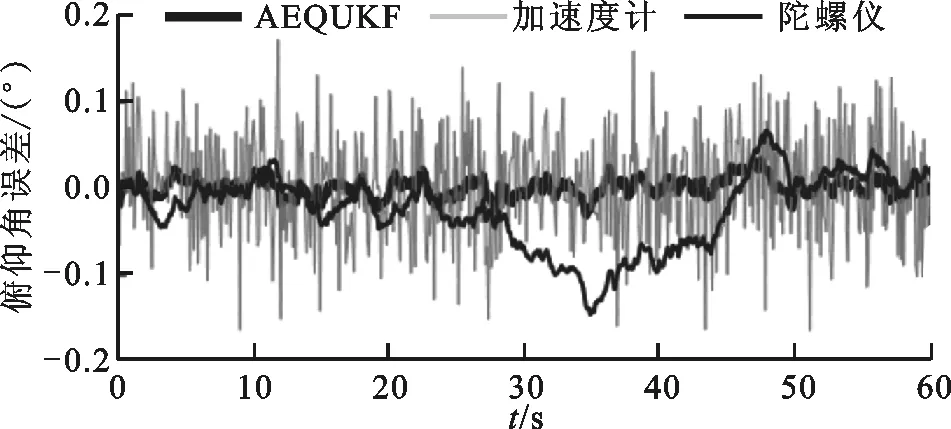
(a)俯仰角誤差

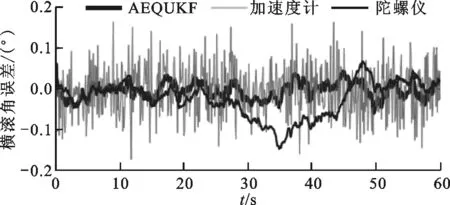
(b)橫滾角誤差

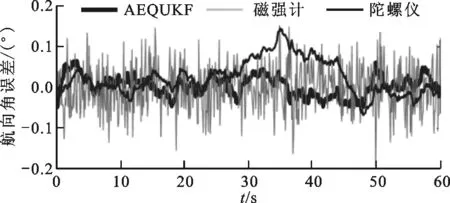
(c)航向角誤差圖2 靜態條件下姿態解算誤差

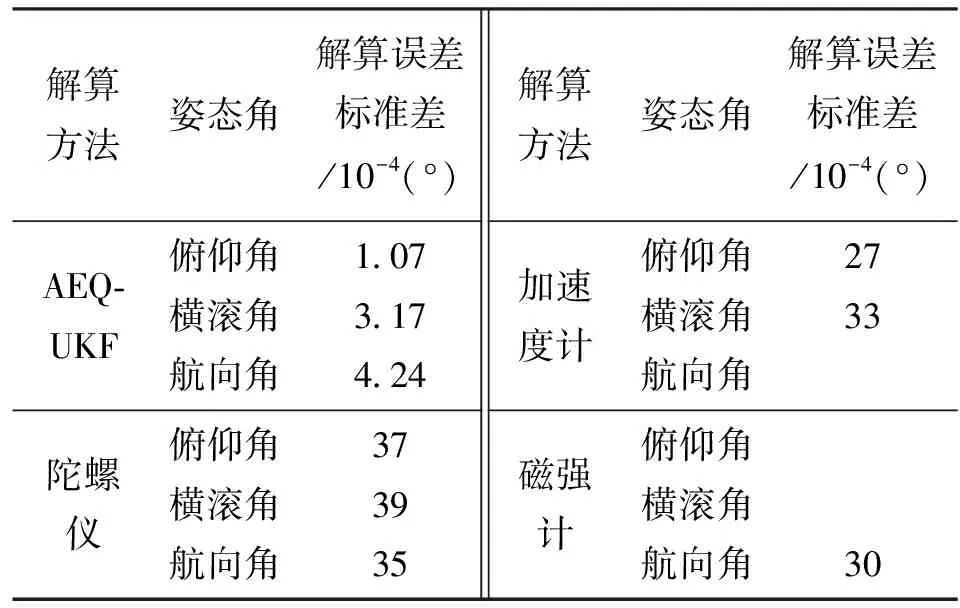
解算方法姿態角解算誤差標準差/10-4(°)解算方法姿態角解算誤差標準差/10-4(°)AEQ-UKF俯仰角橫滾角航向角1.073.174.24加速度計俯仰角橫滾角航向角2733 陀螺儀俯仰角橫滾角航向角373935磁強計俯仰角橫滾角航向角30

3.2 動態驗證

飛行器在加速上升、減速下降等過程中存在較大的非重力加速度。為了驗證提出的方法對非重力加速度有較好的抑制效果,利用Matlab平臺對算法進行仿真驗證。圖3為Matlab仿真中加速度計的輸出噪聲數據,nx、ny、nz分別為加速度計在x、y、z方向的噪聲,可以看出加速度計噪聲部分在閾值范圍外,說明仿真中存在非重力加速度影響。

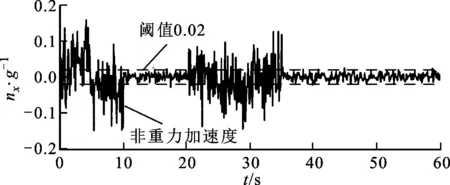
(a)加速度計x方向噪聲

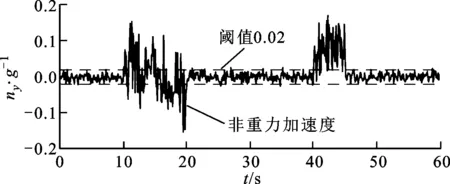
(b)加速度計y方向噪聲

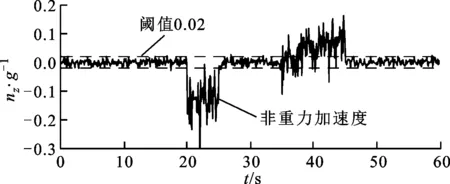
(c)加速度計z方向噪聲圖3 動態條件下加速度計的輸出噪聲

圖4和表2給出了動態非重力加速度仿真中AEQUKF解算結果,可以看出:EQUKF受到非重力加速度影響,濾波精度比較低,而本文提出的AEQUKF可以有效地減小非重力加速度影響,獲得較高的姿態解算精度。

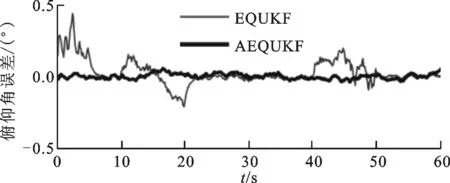
(a)俯仰角解算誤差

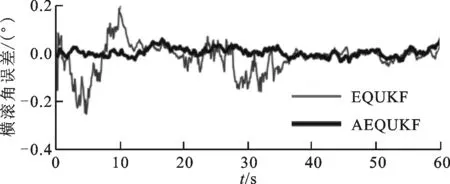
(b)橫滾角解算誤差

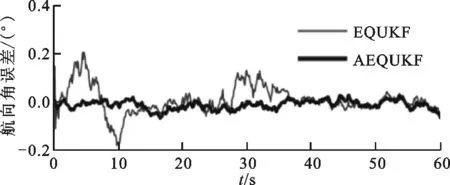
(c)航向角解算誤差圖4 動態條件下姿態解算誤差

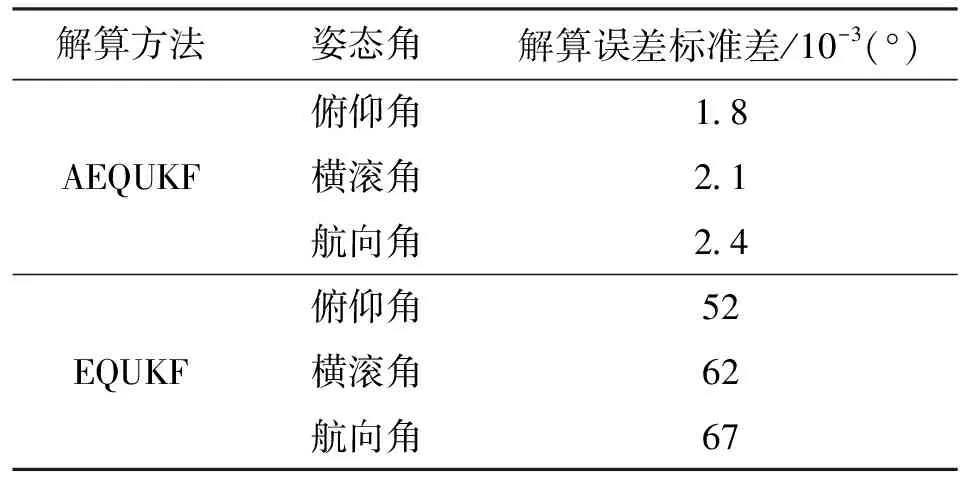
解算方法姿態角解算誤差標準差/10-3(°)俯仰角1.8AEQUKF橫滾角2.1航向角2.4俯仰角52EQUKF橫滾角62航向角67

4 總 結

通過研究飛行器姿態解算時存在非重力加速度影響的問題,提出了AEQUKF飛行器姿態估計算法。在AEQUKF算法中,基于誤差四元數方法構建UKF狀態方程和量測方程。當檢測到存在非重力加速度時,利用殘差信息自適應調整協方差矩陣,減小非重力加速度的影響,獲得較為準確的姿態解算值,有效地減小了陀螺儀漂移誤差帶來的影響。實驗表明,AEQUKF算法對非重力加速度具有很好的補償作用,為飛行器提供了一個低成本、高精度的姿態檢測系統。