鐵路橋梁彈塑性護欄設計及碰撞仿真研究

高廣軍，陳功，關維元，吳永軍

?

鐵路橋梁彈塑性護欄設計及碰撞仿真研究

高廣軍，陳功，關維元，吳永軍

(中南大學 交通運輸工程學院，軌道交通安全教育部重點實驗室，湖南 長沙 410075)

提出一種適用于高速鐵路橋梁彈塑性護欄設計，由立柱、吸能塊和橫梁組成。以3個組成部分的壁厚為設計變量，以吸能量和最大峰值力為目標響應，通過數值仿真得到優化拉丁超立方試驗設計的樣本空間。基于最小二乘法構建關于目標響應的三階多項式響應面模型，通過多目標遺傳算法對彈塑性護欄各組成部分的壁厚進行優化設計。以多目標優化設計的“平衡解”為彈塑性護欄的壁厚尺寸，建立簡化的列車-彈塑性護欄-橋梁有限元模型，通過仿真對比現有防護墻和彈塑性護欄對脫軌列車的防護性能。研究結果表明：彈塑性護欄可以降低列車的撞擊力，同時可以吸收部分碰撞能量。

鐵路橋梁；彈塑性護欄；優化設計；碰撞仿真

為了保證高鐵線路的平直，防止線路沉降，同時為了節約占地面積和不受地形條件的制約，高速鐵路大多建在橋梁上。為了防止列車脫軌脫線后墜落橋底而發生對乘員安全以及財產損失的二次破壞，各國采取了相應的防護措施[1]。德國高速鐵路采用無砟混凝土板式道床，橋面鋪設標準設計的人行道遮板構件，以其電纜槽墻體作為防止列車脫軌的安全措施。瑞典高速鐵路橋面采用加高的現澆擋碴墻來防止列車脫軌后沖出橋面。日本新干線橋面一般采用無砟混凝土板式道床，在明橋面上設有護輪軌。我國在高速鐵路橋梁上主要采用防護墻來防止列車傾覆或沖出橋面，防護墻在鐵路橋梁上的位置如圖1所示。王川[2]對客貨共線鐵路橋梁列車脫軌后與防護墻碰撞過程進行分析，研究了防護墻的高度、考慮道床的下陷和防護墻墻體特征對于脫軌碰撞過程的影響規律。針對鐵路橋梁的防護墻研究較少，但是對于國內外公路上的護欄有大量的研究。杜洋等[3]開展了半剛性護欄系統的沖擊實驗研究，結果表明波形梁的吸能量約為總吸收能量的50%~65%，防阻塊的吸能量約為15%~25%，立柱的吸能量所占的比例很小。YIN等[4?5]基于徑向基函數法對一種新型的η型護欄和一種混凝土護欄進行了優化設計。Wiebelhaus等[6?12]對混凝土護欄、波紋梁護欄和纜索護欄進行了全尺寸的實驗研究。Elvik等[13]基于實際的統計數據研究了半剛性護欄等交通安全設施的有效性，然后提出了一些如何修改這些安全設施的建議。Borovin?k等[14]討論了波紋梁護欄不同截面形狀防阻塊的吸能性能，發現六邊形在能量吸收方面優勢明顯。現有的混凝土防護墻在防護過程中，幾乎不能吸收列車的沖擊動能，同時脫軌列車與混凝土防護墻之間的撞擊力較大，對于整個橋梁強度要求較高。本文提出一種鐵路橋梁段彈塑性護欄，通過響應面模型對彈塑性護欄結構的厚度尺寸進行了優化設計，然后基于CRTSI板式無砟軌道結構形式，建立簡化的列車-彈塑性護欄?橋梁整體有限元模型，LS-DYNA仿真結果表明，設計的彈塑性護欄與原有的橋梁防護墻相比，排障器和后轉向架區域的撞擊力下降，可以對脫軌列車有更好的導向作用，同時彈塑性護欄可以吸收碰撞能量。

圖1 鐵路橋梁防護墻

1 高速鐵路橋梁彈塑性護欄結構設計

本文提出一種適用于高速鐵路橋梁段的彈塑性護欄設計，主要由立柱、吸能塊和橫梁組成。利用SolidWorks和HyperMesh軟件建立彈塑性護欄的幾何模型和有限元模型。圖2所示為立柱模型，立柱的右半部分是一個半徑為50 mm，高為1 000 mm的半圓柱，左半部分的上部是一個尺寸為100 mm ×50 mm×300 mm的方柱，下部是一個斜柱，其中最下端是一個邊長為100 mm的矩形，整個立柱開有14個間隔為20 mm，尺寸為75 mm×20 mm的方孔，立柱厚度定義為。圖3所示為吸能塊模型，吸能塊是一種吸能結構，高300 mm。其中一面是平面通過螺栓連接橫梁，其他3面內凹，橫向方向的凹面對應的圓心角為50°，通過螺栓與立柱連接，縱向方向2個凹面對應的圓心角均為60°，吸能塊的厚度定義為。圖4所示為橫梁模型，橫梁是一種雙波梁的結構形式，高309 mm，波紋深度54 mm，厚度定義為。整個彈塑性護欄是一個薄壁結構，采用四節點的殼單元來模擬，網格大小為20 mm，同時利用MAT_PIECEWISE_LINEAR_ PLASTI- CITY材料定義彈塑性護欄材料屬性。

單位：mm

單位：mm

單位：mm

彈塑性護欄各組成部分的壁厚對于彈塑性護欄的整體吸能性能有較大的影響，因此需要得到一組合適的壁厚值，讓彈塑性護欄的各組成部分都可以充分發揮吸能作用，同時也需要降低脫軌列車與彈塑性護欄之間的撞擊作用力。進行優化設計時，由于立柱開口之后強度變低，立柱的壁厚應當大于吸能塊的壁厚；橫梁由于受到列車的直接沖擊，因此橫梁壁厚也大于吸能塊的壁厚。綜合考慮，立柱厚度和橫梁厚度變化區間為5~12 mm，吸能塊厚度變化區間為2.5~6 mm。

以，和為設計變量，通過優化拉丁超立方試驗設計[15]，得到所有樣本點取值。采用LS- DYNA軟件對彈塑性護欄進行碰撞仿真計算，選取質量為20 t的質量塊，以18 m/s的初速度撞擊立柱間隔為1 m，總跨度6 m的彈塑性護欄，有限元仿真模型如圖5所示。橫梁、吸能塊和立柱之間通過剛性單元進行連接，給立柱底部所有節點施加固定約束。表1詳細的列出了優化拉丁超方試驗設計的樣本點和計算得到的吸能量和最大峰值力。式(1)和式(2)分別為目標響應和與設計變量，和的3階多項式響應面模型函數表達式。

圖5 有限元仿真模型

表1 樣本點取值和仿真結果

代理模型是通過響應近似值對實際響應值的逼近，響應值與真實值存在誤差。本文通過決定系數R和平均相對誤差來評估響應面模型的準確度，2個評價指標的表達式如下所示：

表2 響應面模型的精度

基于響應面模型，以最大的吸能量和最小的峰值力為優化目標，對彈塑性護欄結構的壁厚尺寸進行多目標優化設計。多目標優化的數學模型可以表示為式(5)。

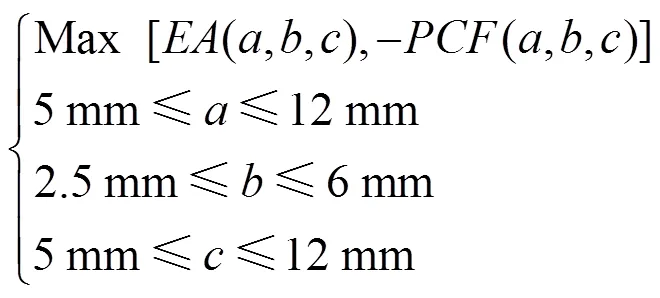
本文采用多目標遺傳算法(MOGA)對壁厚的取值進行多目標優化，得到的Pareto前沿如圖6所示，由圖可知，3階多項式響應面模型的目標響應吸能量和最大峰值力是正相關的。表3列出了不同約束條件下設計變量和目標響應的取值。點的約束條件是最大峰值力達到最小值，對應的設計變量=11.998 mm，=5.995 mm，=5.043 mm。點的約束條件吸能量達到最大值，對應的設計變量=11.995 mm，=5.855 mm，=11.992 mm。

為了在吸能量和最大峰值力之間做出一個合理的平衡，本文基于“距離最小化”標準得到了平衡它們之間相互矛盾的優化解點，“距離最小化”標準滿足以下方程：

圖6 彈塑性護欄的Pareto前沿

Fig. 6 Pareto frontier of the elastic-plastic guardrail

表3 不同約束條件下的彈塑性護欄優化方案

2 總體有限元仿真模型

圖7(a)和7(b)是路基和列車有限元模型。選用曲線半徑為2 200 m，外軌超高150 mm的高速鐵路橋梁段，橋面結構采用的是簡化的CRTSI板式無砟軌道，只考慮了路基在高度方向上的影響。路基轉過的角度為3.334°，由于外軌超高引起5.707°的傾斜角。由于不考慮路基在碰撞過程中變形，因此路基設為剛體，相應的網格大小為50 mm。列車頭車是大型的板、梁空間框架式結構，列車網格大小為50 mm，不考慮接觸失效和懸掛裝置的影響，轉向架考慮為剛體，列車總重45 t。

圖7(c)和7(d)是設計的彈塑性護欄和現有的防護墻有限元模型，距離軌道中心線1 900 mm，防護墻和彈塑性護欄長度取128 m。防護墻采用C50混凝土材料，在LS-DYNA中通過實體單元來模擬，并采用111號材料[2]。彈塑性護欄的材料為Q235，利用殼單元來模擬，壁厚采用上一節Pareto前沿中優化點B的取值。

(a) 路基；(b) 列車；(c) 彈塑性護欄；(d) 防護墻；(e) 耦合系統

脫軌列車、防護設備和路基之間都設有自動面面接觸，彈塑性護欄和脫軌列車本身設有自動單面接觸。彈塑性護欄和防護墻的底部所有節點施加了固定約束，同時定義了脫軌列車沿軸正方向55.55 m/s的運行初速度。列車剛好脫離軌道設為計算的初始時刻[16]，此時輪對橫向偏移60 mm，垂向抬高27 mm。建立好的2種防護形式下的系統有限元模型如圖7(e)所示。

3 仿真結果分析

整個撞擊過程中，混凝土防護墻的吸能量為101 106 J，而彈塑性護欄各組成部分都吸收了沖擊能量，其中立柱的吸能量為712 617 J，吸能塊的吸能量為686 939 J，橫梁的吸能量為430 218 J。彈塑性護欄的吸能量比混凝土防護墻的吸能量有了很大的提升。

如圖8(a)所示是在現有防護墻防護形式下，排障器和防護墻的碰撞力?時間曲線。由于脫軌列車與防護設備之間存在一定的初始距離，列車前端的排障器在1.15 s開始與防護墻發生接觸，各個方向的作用力迅速上升，橫向方向和垂向方向的作用力都為正值，也就是說防護墻防止排障器繼續朝軌道外側偏移，同時防護墻對排障器有一個支持力的作用，方向的摩擦力為負值，與列車前進的方向相反。在1.46 s時，排障器受到的橫向作用力達到最大值102.697 kN，而整個合力在1.41 s時達到最大值為159.124 kN。1.97 s時，列車駛出防護墻和軌道區域，排障器作用力降為0。如圖8(b)所示是在彈塑性護欄防護形式下，排障器和彈塑性護欄的作用力?時間曲線，列車前端的排障器在1.10 s開始與彈塑性護欄發生接觸。在1.51 s時，排障器受到的橫向作用力達到最大值97.018 kN，而整個合力在1.55 s時達到最大值為130.083 kN。與現有防護墻相比，在彈塑性護欄防護作用下，列車排障器受到的橫向作用力最大值下降了5.5%，而受到的總合力最大值下降了18.3%。

(a) 防護墻；(b) 彈塑性護欄

如圖9(a)所示是后轉向架與防護墻之間的作用力?時間曲線，列車后轉向架在1.07 s開始接觸防護墻，橫向作用力在1.11 s達到最大值466.224 kN，合力在1.12 s達到最大值952.842 kN。如圖9(b)所示是后轉向架與彈塑性護欄之間的作用力?時間曲線，列車后轉向架在0.99 s開始接觸彈塑性護欄，橫向作用力在1.30 s達到最大值144.989 kN，合力在1.18 s達到最大值427.141 kN。與現有防護墻相比，在彈塑性護欄防護作用下，列車后轉向架受到的橫向作用力最大值下降了68.9%，而受到的總合力最大值下降了55.2%，下降幅度非常明顯。

(a) 防護墻；(b) 彈塑性護欄

為了更好地掌握防護墻和彈塑性護欄對脫軌列車的導向和保護作用，在列車前后轉向架內側空氣彈簧處分別設置了前后測點。如圖10所示是前后測點橫向位移?時間曲線，1.252 s時，在防護墻防護作用下，前測點橫向位移是1231.22 mm，后測點橫向位移是328.19 mm，前后測點的位移差為903.03 mm。而在彈塑性護欄防護作用下，前測點橫向位移是1 250.81 mm，后測點橫向位移是287.17 mm，前后測點的位移差為963.64 mm。1.752 s時，在防護墻防護作用下，前測點橫向位移是2 361.63 mm，后測點橫向位移是1 341.84 mm，前后測點的位移差為1 019.79 mm，而在彈塑性護欄防護作用下，前測點橫向位移是2 411.30 mm，后測點橫向位移是1 546.35 mm，前后測點的位移差為864.95 mm。前后測點的位移差變小，說明彈塑性護欄對脫軌列車的導向作用更好。

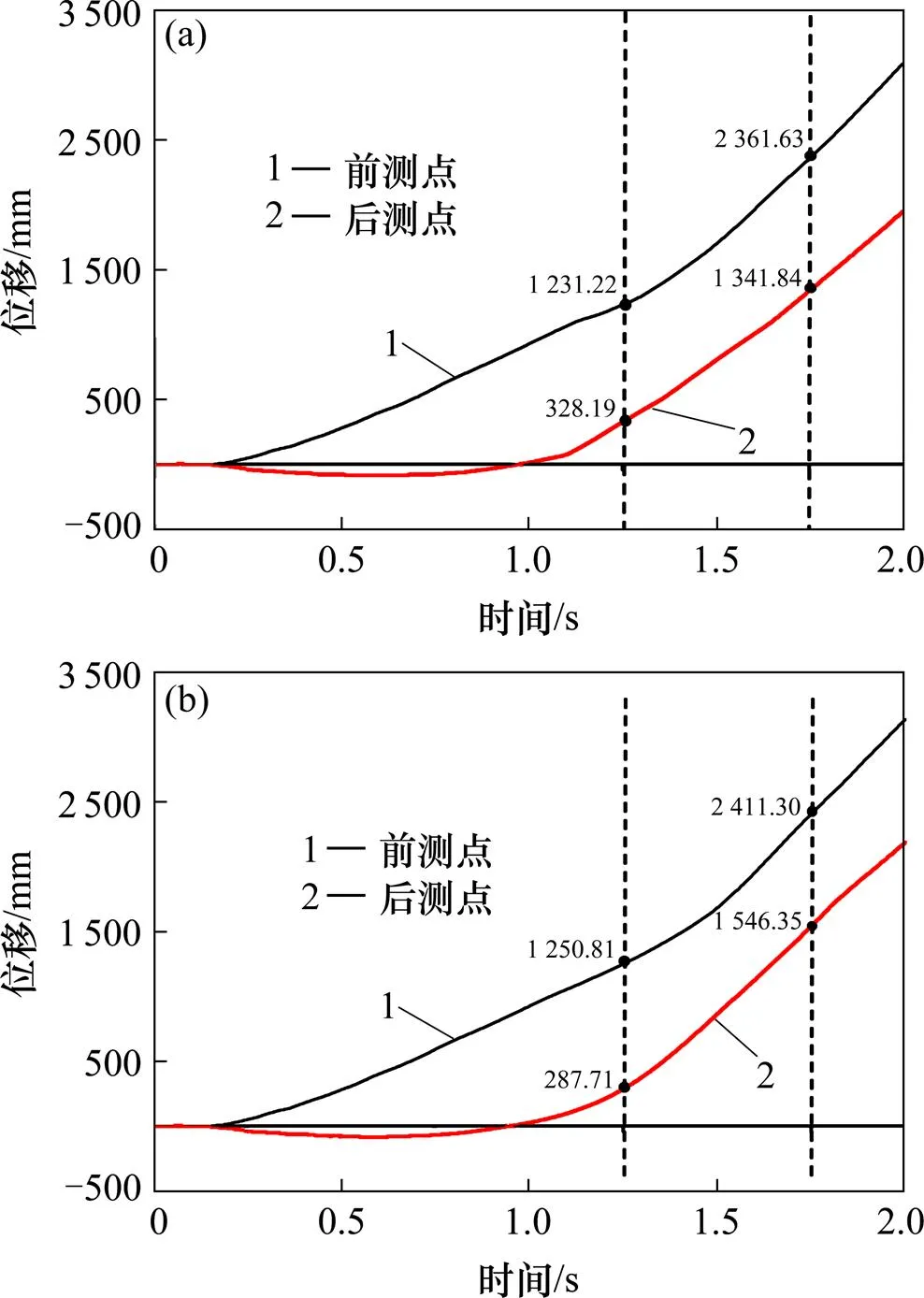
(a) 防護墻；(b) 彈塑性護欄

4 結論

1) 提出一種適用于高速鐵路橋梁彈塑性護欄設計，該護欄由立柱、吸能塊和橫梁組成。以3個組成部分的壁厚為設計變量，通過數值仿真得到優化拉丁超立方試驗設計樣本點的響應值(吸能量和最大峰值力)，基于最小二乘法構建關于目標響應的3階多項式響應面模型，通過多目標遺傳算法對彈塑性護欄的壁厚進行多目標優化設計得到Pareto前沿。

2) 以多目標優化設計的“平衡解”(=10.120 mm，=2.500 mm，=10.800 mm)為彈塑性護欄的壁厚尺寸，建立列車?彈塑性護欄?橋梁的有限元模型，通過仿真對比了現有防護墻和設計的彈塑性護欄對脫軌列車的防護性能，結果表明，彈塑性護欄可以大幅降低列車的撞擊力，其中對排障器的作用力降低了18.3%，對后轉向架的作用力降低了55.2%。

3) 相比現有的防護墻，本文提出的彈塑性護欄對脫軌列車有良好的導向作用，同時可以吸收更多的碰撞能量。

[1] 肖沁凱. 高速鐵路橋梁安全防護措施分析[J]. 鐵道標準設計, 2010(6): 70?72. XIAO Qinkai. Analysis of safety protection measures for high speed railway bridge[J]. Railway Standard Design, 2010(6): 70?72.

[2] 王川. 客貨共線鐵路橋梁列車脫軌后與防護墻碰撞過程研究[D]. 長沙: 中南大學, 2014. WANG Chuan. Research on the process of collision between derailed trains and protective walls on mixed passenger and freight railway bridges[D]. Changsha: Central South University, 2014.

[3] 杜洋, 黃小清, 湯立群. 半剛性護欄系統模型沖擊實驗研究[J]. 華南理工大學學報(自然科學版), 2003, 31(12): 66?70.DU Yang, HUANG Xiaoqing, TANG Liqun. Impact experiment of semi-rigid guardrail system model[J]. Journal of South China University of Technology, 2003, 31(12): 66?70.

[4] YIN Hanfeng, XIAO Youye, WEN Guilin, et al. Design optimization of a new W-beam guardrail for enhanced highway safety performance[J]. Advances in Engineering Software, 2017, 112: 154?164.

[5] YIN Hanfeng, FANG Hongbing, WANG Qian, et al. Design optimization of a MASH TL-3 concrete barrier using RBF-based metamodels and nonlinear finite element simulations[J]. Engineering Structures, 2016, 114: 122?134.

[6] Wiebelhaus M J, Lechtenberg K A, Faller R K, et al. Development of a temporary concrete barrier to permanent concrete median barrier approach transition[R]. Impact Tests, 2010.

[7] Rosenbaugh S K, Faller R K, Bielenberg B W, et al. Development of the MGS approach guardrail transition using standardized steel posts[J]. Highway Safety, 2010.

[8] Wiebelhaus M J, Sicking D L, Faller R K, et al. Phase I: Development of a non-proprietary, four-cable, high tension median barrier[R]. Highway Safety, 2011.

[9] Schmidt J, Sicking D L, Faller R K, et al. Phase II: Development of a non-proprietary, four-cable, high tension median barrier[R]. Highway Safety, 2012.

[10] Stolle C J, Lechtenberg K A, Faller R K, et al. Determination of the maximum mgs mounting height-- Phase I crash testing[R]. Guardrails, 2012.

[11] Julin R D, Faller R K, John R, et al. Determination of the maximum MGS mounting height Phase II detailed analysis[R]. Height, 2012.

[12] Lechtenberg K A, Bielenbery R W, Faller R K, et al. Midwest guardrail system with southern yellow pine posts[R]. Impact Tests, 2013.

[13] Elvik R, Christensen P, Amundsen A. Speed and road accidents: An evaluation of the power model[R]. Nordic Road & Transport Research, 2004.

[14] Borovin?k M, Vesenjak M, Ulbin M, et al. Simulation of crash tests for high containment levels of road safety barriers[J]. Engineering Failure Analysis, 2007, 14(8): 1711?1718.

[15] XU Ping, YANG Chengxing, PENG Yong, et al. Crash performance and multi-objective optimization of a gradual energy-absorbing structure for subway vehicles [J]. International Journal of Mechanical Sciences, 2016, 107: 1?12.

[16] 翟婉明, 陳果. 根據車輪抬升量評判車輛脫軌的方法與準則[J]. 鐵道學報, 2001, 23(2): 17?26. ZHAI Wanming, CHEN Guo. Method and criteria for evaluation of wheel derailment based on wheel vertical rise[J]. Journal of the China Railway Society, 2001, 23(2): 17?26.

Design of elastic-plastic guardrail on the railway bridge and its crash simulation study

GAO Guangjun, CHEN Gong, GUAN Weiyuan, WU Yongjun

(Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

A kind of elastic-plastic guardrail for the high-speed railway bridge is proposed in this paper, which is composed of column, energy absorption block and beam. The wall thicknesses of the three parts were used as the design variables, the(absorbing energy) and the(maximum peak force) as the target response. The optimal Latin hypercube test design, combined with the finite element simulation to get the sample space. Three order polynomial response surface models for target responses were established based on least square method. The multi-objective genetic algorithm was used to optimize the wall thickness of the elastic-plastic guardrail. The “equilibrium solution” of the multi-objective optimization design were set as the wall thickness of the elastic- plastic guardrail, and a simplified train-elastic-plastic guardrail-bridge finite element model was established. The protection performance of the existing protective wall and elastic-plastic guardrail on the derailment train were compared through simulation. The results show that the elastic-plastic guardrail can greatly reduce the impact force of the train and can absorb some collision energy at the same time.

railway bridge; elastic-plastic guardrail; optimal design; crash simulation

10.19713/j.cnki.43?1423/u.2019.02.015

U260

A

1672 ? 7029(2019)02 ? 0391 ? 08

2018?02?01

國家重點研發計劃資助項目(2016YFB1200403)；國家自然科學基金資助項目(U1334208)；中南大學理工醫學科第二批戰略先導立項專項項目(ZLXD2017002)；中國鐵路總公司重點科研項目(2016J009-F)

高廣軍(1973?)，男，河南安陽人，教授，從事列車撞擊動力學研究；E?mail：gjgao@csu.edu.cn

(編輯 涂鵬)