不同需求日高鐵列車開行方案協(xié)同優(yōu)化方法

龍品秀，史峰，胡心磊，徐光明

?

不同需求日高鐵列車開行方案協(xié)同優(yōu)化方法

龍品秀1, 2，史峰1，胡心磊1，徐光明1

(1. 中南大學 交通運輸工程學院，湖南 長沙 410075； 2. 貴陽職業(yè)技術學院 軌道學院，貴州 貴陽 550081)

不同需求日的出行需求在結構和總量上都存在差異，不僅需要提供與各需求日相匹配的運輸能力，而且不同需求日的列車開行方案應有很大相似性，使高鐵運輸組織能平穩(wěn)過渡。為權衡鐵路運營成本和運輸組織銜接，在考慮高鐵運輸組織平穩(wěn)過渡前提下，謀求鐵路運輸成本和旅客出行費用最小，對不同需求日列車開行方案進行協(xié)同優(yōu)化。由各需求日各OD對需求生成最大包絡需求，以最大包絡需求列車開行方案為備選列車集，產(chǎn)生各個需求日的列車開行方案。建立不同需求日開行方案協(xié)同優(yōu)化雙層規(guī)劃模型，設計求解模型的遺傳算法。算例分析表明，在公共列車集比例限制下，協(xié)同優(yōu)化產(chǎn)生的開行方案具有較好評價指標，算法收斂性較好，體現(xiàn)了模型和算法的有效性。

高速鐵路；列車開行方案；協(xié)同優(yōu)化；不同需求日；遺傳算法

高速鐵路需求在總量上有差異性，在非節(jié)假日的一周內(nèi)，周五和周日客流量需求總量較大，為高峰日；周一到周四及周六的客流需求總量接近且相對較低，為平峰日。同時，客流需求在結構上也存在差異性，即使是高峰日也會存在某些時段和O-D的需求低于平峰日對應時段和O-D的需求。針對需求有差異的情況，一方面，可每日采用相同的開行方案，但將造成運能浪費或不足。另一方面，可根據(jù)每日的不同需求特征，相應設計列車開行方案，但高鐵列車開行方案的變化影響到列車運行圖的動態(tài)調整，列車運營調度涉及到工務、電務、機務、車輛以及運輸?shù)炔块T，所以在一段時間內(nèi)，運輸企業(yè)不可能頻繁對開行方案進行大規(guī)模調整，否則會增加運輸企業(yè)組織工作的復雜性，同時破壞旅客出行習慣。考慮到日間需求差異性特征，在現(xiàn)場工作組織中，通常以工作日列車開行方案為基準，以增加列車的形式編制周末或節(jié)假日的列車開行方案。在周末或節(jié)假日的列車開行方案中也許會剔除少量工作日開行的一些列車。增開或剔除列車依賴于人工經(jīng)驗，與客流需求吻合程度不一定得到滿足，且運行效益不一定好。不同需求日列車開行方案的設計要考慮日間需求總量及結構上的差異性、高鐵客流需求時變性及不同需求日開行方案之間的一致性。只考慮單個需求日的列車開行方案優(yōu)化，史峰等[1]綜合考慮企業(yè)利益和旅客需求，建立優(yōu)化列車開行方案的雙層規(guī)劃模型，并設計模擬退火算法求解；Park[2]綜合考慮最小化旅客出行不便度和運營者費用模型，其中出行不便度包括等待時間和換乘時間，優(yōu)化了列車開行方案；付慧伶等[3]通過建立列車備選集來優(yōu)化列車開行方案；FU等[4]依據(jù)列車停站方案設計分層次的列車開行方案；蒲松等[5]綜合使用列生成與行生成策略的啟發(fā)式算法確定列車的運行路徑及停站方案,采用改進分支策略的分支定界算法求解。由于上述研究未考慮到高鐵需求時變特征，不能較好滿足旅客時變需求。針對客流需求時變性，蘇煥銀等[6]將列車開行方案成本表示為列車運行時間和旅客出行費用的總和，引入列車運行方案圖，通過基于時刻表的高鐵客流分配方法[7]，建立了面向時變需求的高速鐵路列車開行方案優(yōu)化方法，Kaspi等[8]考慮旅客出行需求時變性，在不考慮列車能力限制的情況下，以列車和旅客旅行時間的加權成本為目標對列車開行方案進行優(yōu)化，該研究未考慮列車能力與實際情況相差較大。考慮到客流需求的差異性，蒲松等[9]允許客流在一定區(qū)間范圍內(nèi)波動，建立基于動態(tài)客流的高速列車開行方案的魯棒優(yōu)化模型，該研究未需求考慮超出區(qū)間范圍波動時的情況；Schobel[10]指出針對不確定有差異性的數(shù)據(jù)，采用魯棒優(yōu)化進行處理是一種有效手段。屈明月等[11]指出客流需求是決定實施分號運行圖的必要條件，指出京廣、京滬高鐵客流存在周分布規(guī)律，提出分號運行圖的開設周期與客流分布規(guī)律相吻合時才可以實施分號運行圖；張琳奇等[12]通過列車保留、取消、調整等手段在平日列車開行方案上生成節(jié)假日列車開行方案。目前對不同需求日列車開行方案研究較為缺乏，均只是對該問題涉及到部分特征有所探討，尚未有人同時兼顧日間需求變化與日內(nèi)時變需求進行開行方案設計。針對不同需求日之間的出行需求在結構和總量上差異性，本文從協(xié)同優(yōu)化不同需求日列車開行方案角度出發(fā)，以各需求日各OD對需求生成的最大包絡需求為基礎，利用已有模型優(yōu)化列車開行方案，得到最大包絡需求方案，將最大包絡需求開行方案為作為備選列車集，優(yōu)選產(chǎn)生各個需求日的開行方案。以不同需求日列車運行總成本、旅客出行費用總成本為目標，構建不同需求日開行方案之間的協(xié)同優(yōu)化雙層規(guī)劃模型，將原模型轉為罰函數(shù)模型利用遺傳算法求解。算例分析表明，在規(guī)定的公共列車集比例限制下，協(xié)同優(yōu)化產(chǎn)生的開行方案具有較好的評價指標，算法收斂性較好。

1 問題描述

綜上所述，可將不同需求日高鐵列車開行方案協(xié)同優(yōu)化問題描述如下：

2 問題分析

2.1 平穩(wěn)過渡的量化描述

2.2 先總后分的求解思路

具有很相近品質的列車開行方案可以有多種列車組合形式，若分別優(yōu)化每一個需求日的開行方案，則難保證各個需求日開行方案具有足夠大的公共列車集。為解決這個問題，不同需求日的現(xiàn)行開行方案，主要是在工作日開行方案的基礎上增加開行列車，獲得周末列車開行方案。在此基礎上進行擴展，采用先總后分的思路協(xié)同求解：首先，構建一個不小于任意需求的總需求，基于總需求優(yōu)化產(chǎn)生一個開行方案；然后對于每一個需求日，以總需求開行方案的子集構造其列車開行方案，使得公共列車集的規(guī)模必須滿足規(guī)定標準；最后，可對于每一個需求日的開行方案進行適當調整，獲得各個需求日的最終開行方案。

2.3 總需求的生成方法

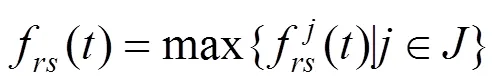
2.4 最大包絡需求開行方案的求解

對于給定的最大包絡需求，可以參照文獻[6]的方法優(yōu)化求解最大包絡需求開行方案。文獻[6]為傳統(tǒng)開行方案引入列車始發(fā)時刻的預估值，以便評價列車開行方案的時變需求的吻合程度。將開行方案的優(yōu)化問題描述為主從博弈，其中鐵路運輸企業(yè)為主體方，出行旅客為從屬方。鐵路運輸企業(yè)考慮全天運營時間約束、每個線路區(qū)間上每天和每個時段的列車通過能力約束、每趟列車在車站的到達和出發(fā)時刻的相互關系、每個車站始發(fā)(或終到)列車總數(shù)約束、動車組周轉約束，以旅客出行費用和折算動車組小時數(shù)為目標優(yōu)化開行方案，旅客出行費用由基于列車時刻表的客流分配確定(見文 獻[7])。

3 不同需求日列車開行方案協(xié)同優(yōu)化模型

根據(jù)上述分析，構建不同需求日列車開行方案的協(xié)同優(yōu)化模型如下。

3.1 約束條件

1) 公共列車集比例下限約束

其中：||為列車的公里數(shù)。

2) Ω為Ω的子方案約束

3) 全天區(qū)間通過能力約束

記列車開行方案Ω全天進入?yún)^(qū)間的列車數(shù)為T，T受通過能力C()的限制，即

4) 車站始發(fā)和終到的列車總數(shù)約束

車站的始發(fā)和終到列車數(shù)不能超過車站始發(fā)終到能力C的限制，即

3.2 協(xié)同優(yōu)化模型

協(xié)同優(yōu)化目標是每一個開行方案的旅客出行費用和鐵路運輸成本達到最小，這是一個多目標優(yōu)化問題。由于各個需求日的重要程度由這些需求日的天數(shù)比例確定，只要以天數(shù)比例為權值，便可獲得旅客出行費用加權總量和鐵路運輸成本的加權總量。進而，引入旅客出行費用和鐵路運輸成本的權重系數(shù)，對二者加權匯總，將這個多目標優(yōu)化問題轉化為單目標優(yōu)化問題。

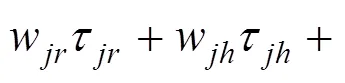
其中：，τ，τ由開行方案Ω對應列車網(wǎng)絡上的客流分配確定。

4 協(xié)同優(yōu)化的遺傳算法

4.1 罰函數(shù)模型的轉化

為了方便求解協(xié)同優(yōu)化的雙層規(guī)劃模型，由式(4)，(6)~(9)構建罰函數(shù)

將原模型轉化為罰函數(shù)雙層規(guī)劃模型如下：

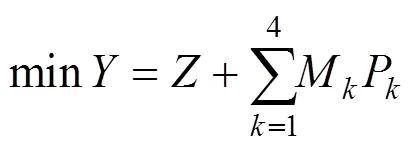
4.2 遺傳算法設計

鑒于模型的求解復雜度高，選擇常規(guī)遺傳算法求解。

1) 基因編碼

2) 初始種群

一般而言，初始種群多采用隨機方法生成。雖然基因編碼方法使約束條件(5)得到滿足，使罰函數(shù)雙層規(guī)劃模型變成無約束優(yōu)化問題，但事實上的約束是存在的，應該在盡可能滿足約束條件、考慮目標函數(shù)最優(yōu)性的條件下隨機生成初始種群。

針對約束條件(6)~(8)，生成初始種群時只要求在一定精度上得到滿足。一方面不嚴格滿足約束條件能擴大解的提高搜索能力；另一方面也難于尋找嚴格滿足各項約束的可行解；

針對目標函數(shù)最優(yōu)性，在給定平均客座率標準的基礎上，將不同需求日的人公里數(shù)換算成動車組公里數(shù)，為不同需求日配備相應的運輸能力。

上述初始種群的生成方法既適當考慮了約束條件和目標函數(shù)的最優(yōu)性，又避免了下層規(guī)劃客流分配的大計算量。

3) 適應度函數(shù)

以目標函數(shù)()的倒數(shù)設計基因編碼的適應度函數(shù)()，即

若目標函數(shù)值()越小，則適應度函數(shù)()值越大。

4) 遺傳策略

選擇策略：采用輪盤賭法則進行選擇，選中個體的概率

交叉策略：對于2個父代采用單點交叉法，以給定概率p對遺傳基因進行交叉操作。

變異策略：對于個體上的每個基因以給定概率p對其進行變異操作。

5 算例分析

5.1 算例數(shù)據(jù)

在不同需求日列車開行方案協(xié)同優(yōu)化模型中，設置目標函數(shù)的參數(shù)=1 000，=1，旅客出行單位時間價值w=1元/min，w=2元/min，w=3元/min，16輛編組列車運行時間成本系數(shù)=1.5。首先求得列車的最大包絡需求開行方案，下行方向的列車方案圖如圖2所示。

圖1 京滬高鐵線路

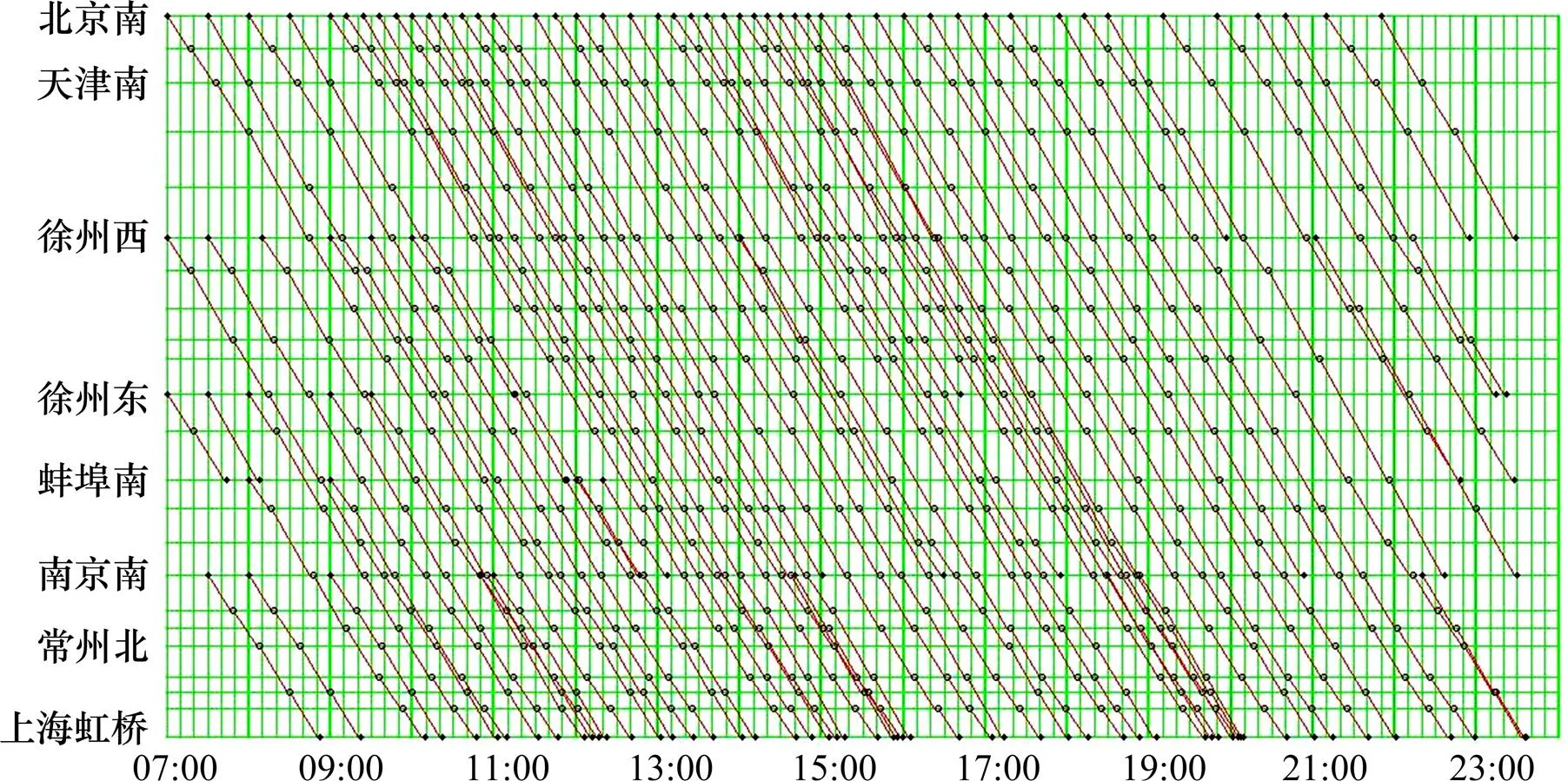
圖2 最大包絡需求列車運行方案圖(下行方向)

5.2 算例計算與分析

設置遺傳算法的種群個數(shù)為50，交叉概率p=0.618，變異概率p=0.03，1=2=0.5，分別針對公共列車集比例下限=0.9，0.8求解2套列車開行方案，并相應記為優(yōu)化方案1和優(yōu)化方案2。優(yōu)化方案1中周一、周五的下行方向開行方案分別如圖4和圖5所示，圖中實心點表示列車的始發(fā)終到站，空心點表示列車停靠站。

算法采用C#編程實現(xiàn)，運用主頻為3.20 GHz，內(nèi)存為4 GB，CPU為雙核的計算機，優(yōu)化方案1迭代500次，程序運行時間大約為10 h，收斂過程如圖3所示(優(yōu)化方案2收斂過程類似)，算法有較好收斂效果。

圖3 搜索方案收斂圖

圖4 周一列車運行方案圖(下行方向)

圖5 周五列車方案圖(下行方向)

優(yōu)化方案1、優(yōu)化方案2及評價指標分別展示在表1及表2中。最大包絡需求開行方案的各項費用比周一、周五開行方案更高。在優(yōu)化方案1中，周五比周一多開行6列列車，公共列車集比例為0.91；在優(yōu)化方案2中，公共列車集比例為0.81，周五比周一多開行8列列車。開行方案的旅客出發(fā)時間偏差均在30 min以內(nèi)，平均客座率均在70%以上，說明2 d開行方案與旅客出行需求的時變性吻合較好。優(yōu)化方案1與優(yōu)化方案2相比，公共列車集比例下限從0.9降到0.8，但周一方案的總費用由6.32×107降到5.69×107，動車組小時數(shù)由678.1組?h下降到597.1組?h，列車總數(shù)由121列減少到115列，旅客平均出發(fā)時間偏差由18.39 min增加到22.56 min，旅客出行總費用由2.24×103萬元減少到2.11×103萬元，客座率由72.44%增加到73.07%。周五方案也具有類似性質。因此，通過提高公共列車集比例下限，可以獲得開行方案間的更大列車公共交集，但是會增加各方案的總費用。可根據(jù)實際需要，調整的值，獲得滿意的方案。

表1 優(yōu)化方案1評價指標

表2 優(yōu)化方案2評價指標

6 結論

1) 為保證不同需求日之間運輸組織平穩(wěn)過渡，提出由各需求日各O-D對需求生成最大包絡需求，以最大包絡需求列車開行方案為備選列車集，優(yōu)選產(chǎn)生各個需求日的列車開行方案的協(xié)同優(yōu)化思想。

2) 以各需求日運輸成本、旅客出行成本為目標，建立了不同需求日列車開行方案協(xié)同優(yōu)化雙層規(guī)劃模型，并設計了協(xié)同優(yōu)化的遺傳算法，在公共列車集達到規(guī)定比例的限制下，從最大包絡需求列車開行方案中優(yōu)化生成各需求日的列車開行方案。

3) 以京滬高鐵線路為例驗證了模型的正確性和算法的有效性。算例分析表明，協(xié)同設計不同需求日的列車開行方案能較好吻合客流的時變需求，且互相之間能保持較好一致性。

[1] 史峰, 鄧連波, 霍亮, 等. 旅客列車開行方案的雙層規(guī)劃模型和算法[J]. 中國鐵道科學, 2007, 28(3): 110?116. SHI Feng, DENG Lianbo, HUO Liang, et al. Bi-level programming model and algorithm of passenger train operation plan[J]. China Railway Science, 2007, 28(3): 110?116.

[2] Park B H, Seo Y I, Hong S P, et al. Column generation approach to line planning with various halting patterns—application to the Korean high speed railway[J]. Asia-Pacific Journal of Operational Research, 2013, 30(4): 1?19.

[3] 付慧伶, 聶磊, 楊浩, 等. 基于備選集的高速鐵路列車開行方案優(yōu)化方法研究[J]. 鐵道學報, 2010, 32(6): 1?8. FU Huiling, NIE Lei, YANG Hao, et al. Research on the method for optimization of candidate-train-set based train operation plans for high-speed railways[J]. Journal of the China Railway Society, 2010, 32(6): 1?8.

[4] FU H, NIE L, MENG L, et al. A hierarchical line planning approach for a large-scale high speed rail network: The China case[J]. Transportation Research Part A, 2015, 5(75): 61?83.

[5] 蒲松, 呂紅霞, 陳釘均, 等. 基于改進列生成算法的高速列車開行方案優(yōu)化研究[J]. 鐵道學報, 2015, 37(9): 1?7. PU Song, Lü Hongxia, CHEN Dingjun, et al. Highspeed railway passenger train line planning optimization based on improved column generation algorithm[J]. Journal of the China Railway Society, 2015, 37(9): 1?7.

[6] 蘇煥銀, 史峰, 鄧連波, 等. 面向時變需求的高速鐵路列車開行方案優(yōu)化方法[J]. 交通運輸系統(tǒng)工程與信息, 2016, 16(5): 110?116. SU Huanyin, SHI Feng, DENG Lianbo, et al. Time-dependent demand oriented line planning optimization for the high-speed railway[J]. Journal of Transportation Systems Engineering and Information Technology, 2016, 16(5): 110?116.

[7] SU H Y, SHI F, XU G M, et al. Schedule-based passenger assignment for high-speed rail networks considering the ticket-booking process[J]. Mathematical Problems in Engineering, 2016, 1(1): 1?15

[8] Kaspi M, Raviv T. Service-oriented line planning and timetabling for passenger trains[J]. Transportation Science, 2013, 47(3): 295?311.

[9] 蒲松, 王文憲, 陳釘均, 等. 高速旅客列車開行方案的魯棒優(yōu)化模型[J]. 交通運輸系統(tǒng)工程與信息, 2015, 15(6): 101?106. PU Song, WANG Wenxian, CHEN Dingjun, et al. The Robust model for line planning problems of high speed passenger train[J]. Journal of Transportation Systems Engineering and Information Technology, 2015, 15(6): 101?106.

[10] Sch?bel A, Scholl S. Line planning with minimal traveling time[C]// ATMOS 2005-5th Workshop on Algorithmic Methods and Models for Optimization of Railways, 2006.

[11] 屈明月, 黃樹明. 基于周期天窗的高速鐵路分號運行圖研究[J]. 鐵道運輸與經(jīng)濟, 2013, 35(12): 10?13. QU Mingyue, HUANG Shuming. Study on variant train working diagram of high-speed railway based on periodical maintenance window[J]. Railway Transport and Economy, 2013, 35(12): 10?13.

[12] 張琳奇, 聶磊, 付慧伶, 等. 高速鐵路節(jié)假日列車開行方案優(yōu)化研究[J]. 鐵道運輸與經(jīng)濟, 2017, 39(11): 57?62.ZHANG Linqi, NIE Lei, FU Huiling, et al. Optimization model for high-speed railway line planning during holidays[J]. Railway Transport and Economy, 2017, 39(11): 57?62.

The collaborative optimization of multi-day line plannings for high-speed railway

LONG Pinxiu1, 2, SHI Feng1, HU Xinlei1, XU Guangming1

(1. School of Traffic and Transportation Engineering, Central South University, Changsha 410075, China; 2. Rail Transportation Branch, Guiyang Vocational and Technical College, Guiyang 550081, China)

The differences of passenger demand among multi-day in passenger flow volume and time-varying structure requires that line plannings among multi-day can provide the corresponding capacity. Meanwhile, line plannings among multi-day need to have a lot of similarities to ensure the transport organizations can transit smoothly. In order to coordinate the railway operating costs and transport organizations cohesion, the railway operation costs and travel expenses of passengers are minimized on the premise of a smooth transition of high-speed rail transport organizations of multi-day. The collaborative optimization method of multi-day line plannings is carried out. In this method, each OD needs to generate the maximum demand for each day and solve the maximum demand line planning as a candidate train set, then the line planning for each day is preferably generated. The collaborative optimization bi-level programming model was established based on the multi-day and design the genetic algorithm to solve the model. The numerical example shows that under the constraint of the proportion of public train set, the line plannings which are produced by collaborative optimization method have good evaluation indexes, and the convergence of the algorithm shows the validity of the model and the algorithm.

high-speed railway; line planning; collaborative optimization; multi-day; genetic algorithm

10.19713/j.cnki.43?1423/u.2019.02.005

U293.32

A

1672 ? 7029(2019)02 ? 0310 ? 09

2018?03?05

國家自然科學基金資助項目(U1334207，71701216)

史峰(1956?)，男，湖南芷江人，教授，博士，從事交通流理論，運輸網(wǎng)絡優(yōu)化研究；E?mail：shifeng@csu.edu.cn

(編輯 蔣學東)