刨削式吸能結構用45號鋼高應變率高溫力學行為與本構模型研究

何曉蕾，司志強，陳璇臻，彭珊，彭勇，許平

?

刨削式吸能結構用45號鋼高應變率高溫力學行為與本構模型研究

何曉蕾1，司志強1，陳璇臻2，彭珊2，彭勇2，許平2

(1. 中車唐山機車車輛有限公司，河北 唐山 063000； 2. 中南大學 軌道交通安全教育部重點實驗室，交通運輸工程學院，湖南 長沙 410075)

為研究刨削式吸能結構用45號鋼在不同應變率和不同溫度下的力學行為，對該材料進行實驗與本構模型研究。開展在不同應變率下(10?4s?1~1 500 s?1)和不同溫度下(300~600 ℃)的拉伸實驗。研究結果表明：刨削式吸能結構用45號鋼為應變率敏感型材料。隨著應變率的提高，材料屈服強度和極限強度有著明顯提高，而溫度升高則會使材料軟化降低材料強度。基于實驗結果，建立Johnson-Cook(J-C)本構模型來描述材料流變應力與應變率和溫度之間的關系，并對溫度軟化參數進行線性修正，對率敏感性參數進行了二元二次回歸修正。誤差分析表明修正后的J-C本構模型在預測不同應變率下材料的力學特性時有更高的精確度。

刨削式吸能結構用45號鋼；SHTB；本構模型；Johnson-Cook修正模型

耐撞性吸能裝置在列車發生碰撞時吸收碰撞動能，降低列車事故，從而最大限度地降低人員損傷。對列車吸能裝置的研究，能提高列車被動安全防護技術，為提高列車運營安全性有著重要的研究意義。刨削式吸能是近幾年研究的一種新式吸能方式，已有研究表明該方式優于壓潰型和破裂型吸能方式[1]。常寧等[2]利用金屬切削吸能原理，提出了一種用于軌道車輛被動安全的新型吸能裝置。雷成等[3?5]通過顯示有限元數值模擬，利用多元線性回歸分析方法，研究了刀具前角、切削圓心角、切削深度、切削速度等因素對切削過程和吸能特性的影響。刨削式吸能結構用45號鋼是一種廣泛運用機械制造的優質碳素結構用鋼，具有較高的強度和良好的切削性能。在列車碰撞過程中，吸能裝置在高應變率下發生變形，因此應變率對材料力學行為的影響不能忽略。QIN等[6]通過霍普金森拉桿研究了高強度雙相鋼在高應變率下的應變率效應，研究結果表明DP700和DP5008有著顯著的應變率效應。HU等[7]研究了AerMet100鋼在不同應變率下的動態力學性能，建立了AerMet100鋼率相關性的本構模型，結果表明AerMet100鋼是應變率敏感性材料，Johnson-Cook本構模型比Cowper-Symonds模型更能準確的描述AerMet100鋼在不同應變率下的本構關系。Singh等[8]采用改進的霍普金森桿，研究了多相高強度鋼在不同應變率下動態拉伸行為，發現MP800鋼對應變率效應并不敏感。Akbari等[9]研究了微合金碳鋼在高溫下不同應變率的力學性能，建立了描述材料在高溫變形下的本構關系，結果表明該碳鋼是敏感型材料。李國和等[10]研究了淬硬45鋼在溫度20~800 ℃和應變率10?3，104s?1下動態力學性能，基于高斯函數建立了修正Johnson-Cook模型，研究表明淬硬45鋼對應變率敏感性一般，而對溫度效應有較強敏感性。林莉等[11]通過研究Q235B鋼應變率和溫度效應，確定了Q235B鋼Johnson-Cook模型參數，結果發現Q235B鋼隨著應變率的提高，強度提高，延性降低。由此可見，已有對刨削式吸能結構研究主要針對于結構件的碰撞響應特性以及吸能特性，關于刨削式吸能結構用45號鋼的力學響應特性研究較少，鋼的應變率敏感性與溫度的軟化效應對材料力學行為特性影響尤為重要。本文采用MTS landmark萬能實驗機和分離式霍普金森拉桿(SHTB)系統，進行了刨削式吸能結構用45號鋼在準靜態至高應變率下的(10?4s?1~ 1 500 s?1)拉伸實驗，分析了刨削式吸能結構用45號鋼在不同應變率下的動力學響應特性。另外開展了高溫環境下(300~600 ℃)材料的準靜態拉伸實驗。基于不同應變率和不同溫度下的實驗結果，建立了材料的Johnson-Cook模型。對原模型的溫度軟化參數進行系數修正，引入函數對率敏感性參數進行二元二次多項式修正，得到了應變硬化與應變率耦合效應的Johnson-Cook修正模型。

1 實驗方法

1.1 實驗材料及試樣

選取車用刨削式吸能結構用45號鋼作為研究對象，其他化學成分質量分數為：C=0.42%~0.50%，Si=0.17%~0.37%，Mn=0.50%~0.80%，P≤0.035%，S≤0.035%，Cr≤0.25%，Ni≤0.30%，Cu≤0.25%。其彈性模量為210 GPa，泊松比為0.269。試件幾何示意如圖1~3所示。

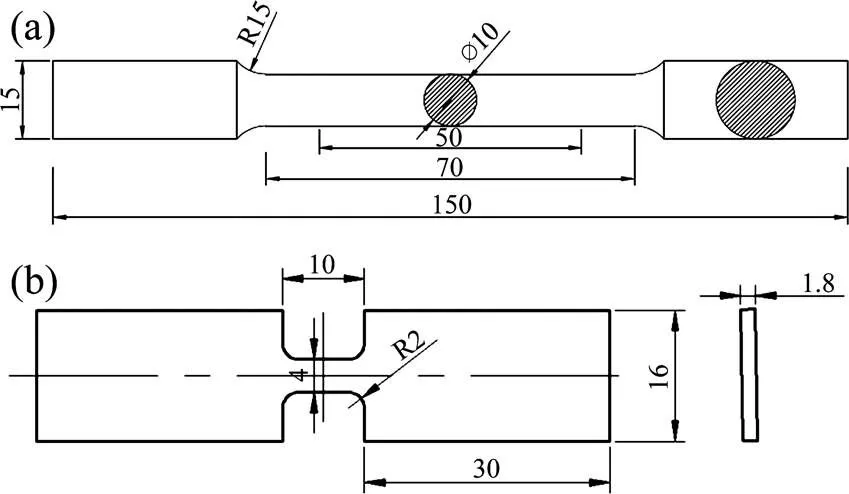
(a) 中低應變率實驗；(b) 高應變率實驗

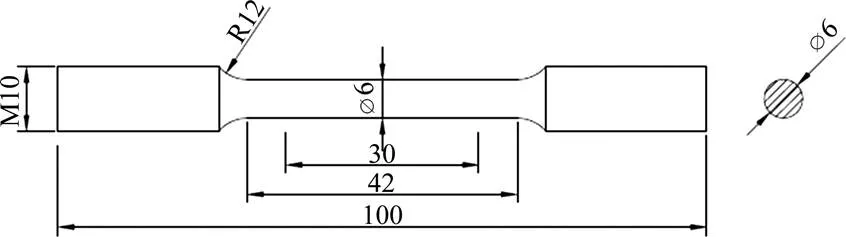
圖2 高溫拉伸實驗試件

1.2 實驗條件

中低應變率拉伸實驗在MTS landmark力學實驗機上進行，高溫拉伸實驗加入高溫爐進行，實驗裝置如圖3所示。高應變率拉伸實驗在分離式霍普金森拉桿系統(SHTB)上進行。分離式霍普金森拉桿裝置示意圖如圖4所示，利用高壓氣體推動套筒式子彈向右運動，撞擊入射桿端頭的法蘭，在入射桿中形成向左傳播的拉伸加載波，貼于入射桿表面的應變片記錄入射信號和反射信號，貼于透射桿上的應變片記錄透射信號。應變信號經超動態應變儀放大，由示波器存儲和記錄，最后由接口傳入計算機進行處理。試驗中試件通過膠接方式被固定在入射桿和透射桿之間。

圖3 高溫拉伸實驗裝置

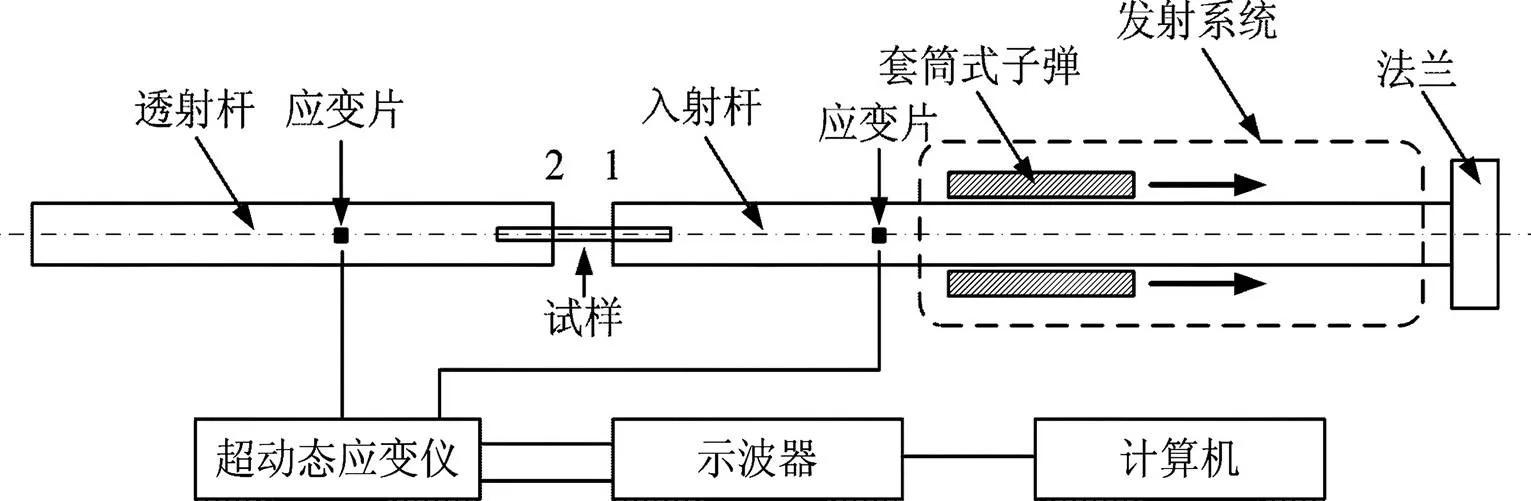
圖4 SHTB實驗裝置測量原理示意

基于一維應力波理論和應力應變軸向均勻分布特性。工程應力、工程應變和應變率可以通過以下等式計算

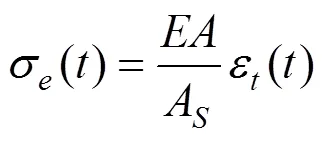
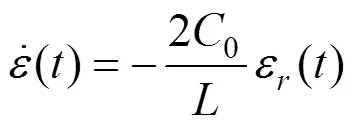
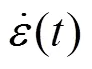
2 實驗結果分析

2.1 應變率相關性分析

通過拉伸實驗獲得刨削式吸能結構用45號鋼在不同應變率下名義應力應變關系。通過塑形段變形體積不變原理，得到關系式(2)[12]，將不同應變率下拉伸實驗所得刨削式吸能結構用45號鋼名義應力應變曲線計算得到真實應力應變曲線。

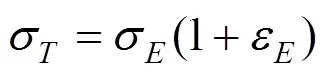
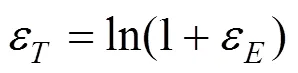
式中：和ε分別為工程應力和工程應變；σ和ε分別為真實應力和真實應變。

圖5比較了不同應變率下材料的真實應力?應變曲線，可以看出隨著應變率升高，刨削式吸能結構用45號鋼的屈服強度和極限強度明顯提高，應變硬化特征發生明顯變化。表1為材料在不同應變率下強度極限及屈服極限。

2.2 溫度效應分析

通過開展4組不同溫度(300~600 ℃)的高溫準靜態拉伸實驗。將同溫度下的實驗數據取平均并計算其工程應力應變關系，結果如圖6所示。

隨著溫度的升高材料的強度不斷下降，材料延性升高，伸長量明顯增加。說明該材料有明顯的溫度軟化效應。材料在高溫拉伸條件下頸縮出現較早，不能用式(2)來計算其真實應力應變，所以僅用屈服點數據確定本構模型溫度軟化參數。

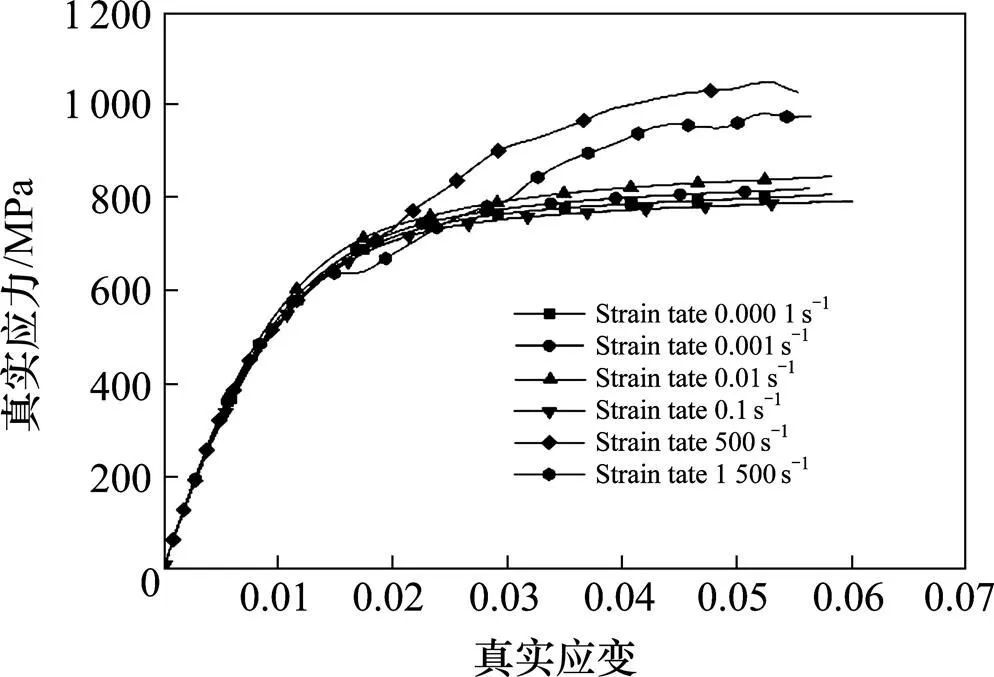
圖5 不同應變率下材料的真實應力-應變曲線對比

表1 刨削式吸能結構用45號鋼在不同應變率拉伸下的屈服強度及極限強度

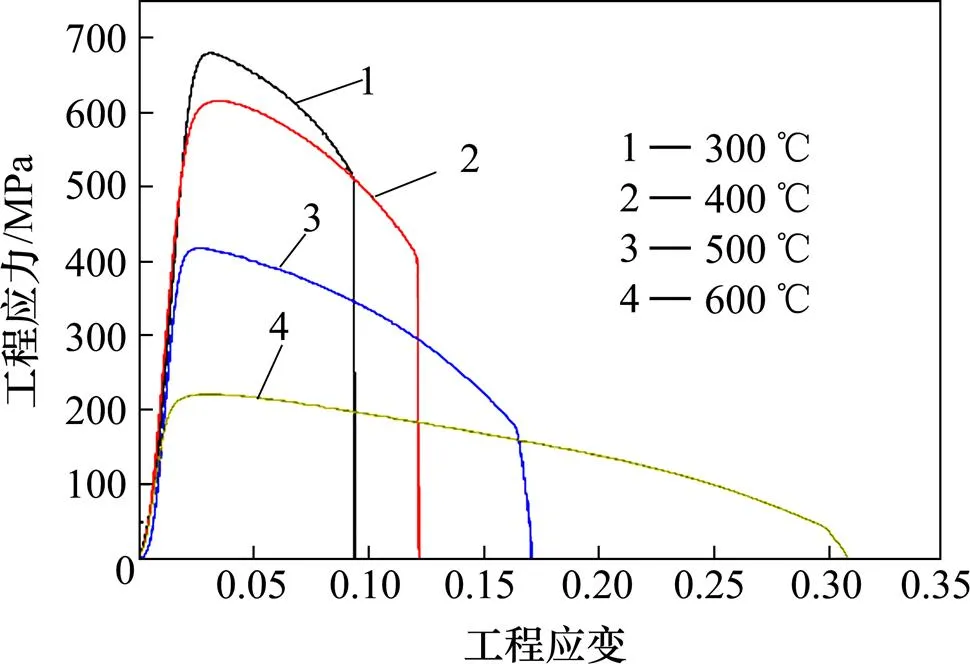
圖6 不同溫度下拉伸實驗工程應力應變曲線

3 本構模型建立

3.1 Johnson-Cook模型及參數確定

材料本構模型描述了材料應力應變關系。在研究結構吸能特性中，準確地描述材料本構關系，是保證有限元數值模擬分析精確可靠的關鍵。對材料本構關系研究主要分為基于經驗和觀察的現象學模型,例如Johnson-Cook[13]模型、Cowper-Symonds[14]等，與基于本質現象的物理模型，例如Gurson模型[15]，Zerilli-Armstrong模型[16]等。選擇合適的材料本構模型，不僅能準確地反映材料力學性能，還能為有限元精確分析及工程合理運用奠定基礎。Johnson-Cook模型是基于經驗描述材料力學行為的本構模型，由于其形式簡單、方便使用而廣泛運用于工程之中[17?20]。該模型是一種經驗型本構模型，考慮材料應變硬化效應、應變率效應及溫度效應對材料力學性能的影響，其表達式為

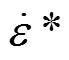
1) 確定參數，和

45號鋼的Johnson-Cook本構模型參數，和可以通過室溫下的拉伸實驗結果來確定，當環境溫度為室溫時本構模型表達式可以簡化為

對于準靜態下的拉伸實驗，其應變率即為參考應變率，因此本構模型可以進一步簡化為

這里是準靜態拉伸實驗中材料的屈服強度，=570.47 MPa。參數和可以通過對真實應力真實應變曲線擬合來確定。擬合得到=689.65 MPa和=0.349 6。

2) 確定參數

對于本構模型溫度相關參數，選用不同溫度下材料的拉伸實驗數據進行擬合。該組拉伸實驗均為準靜態拉伸，本構模型可以改寫為

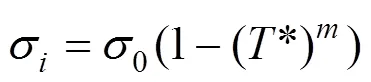
其中：0為室溫環境下準靜態拉伸屈服強度；為不同溫度下材料的屈服強度，對式(6)重新整理并取對數可以改寫為以下形式

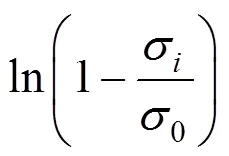
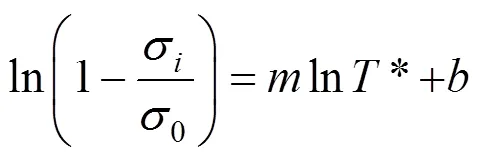
原本構模型變為

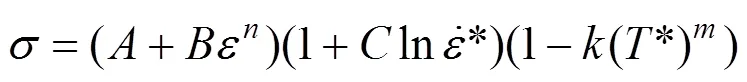
其中：為修正系數，計算公式為=e。

原始結果與修正結果在圖8中進行比較，實線表示原始模型的擬合結果，得到=1.637，決定系數2=0.781；虛線表示修正后的擬合結果，得到=4.949，=4.394，決定系數2=0.969。圖8中給出了各溫度下原始模型屈服應力與修正模型屈服應力，通過對比可以看出修正后的模型能更好的預測不同溫度下材料的屈服應力。

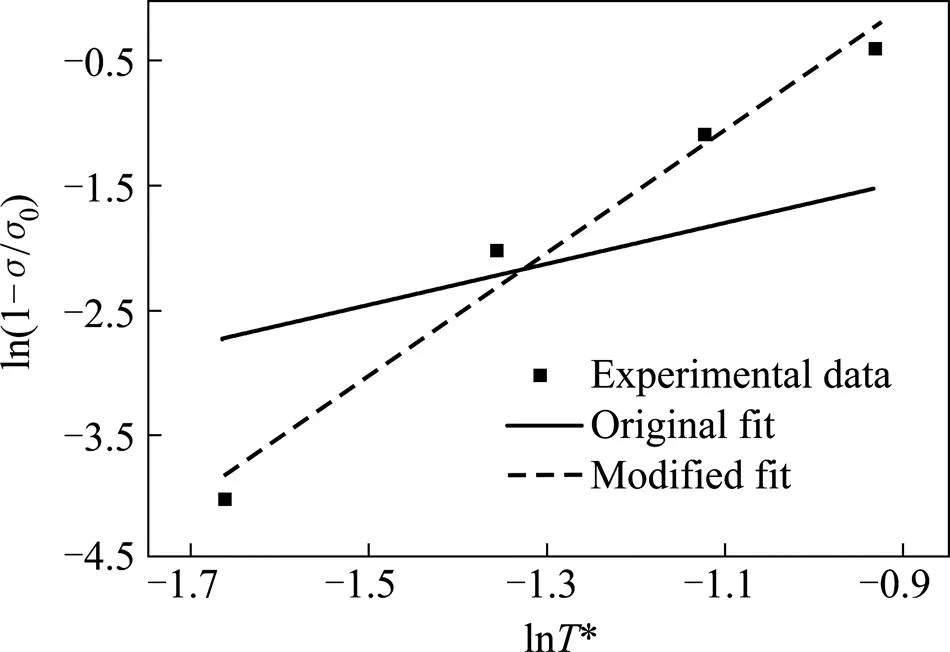
圖7 本構模型溫度相關性系數修正對比

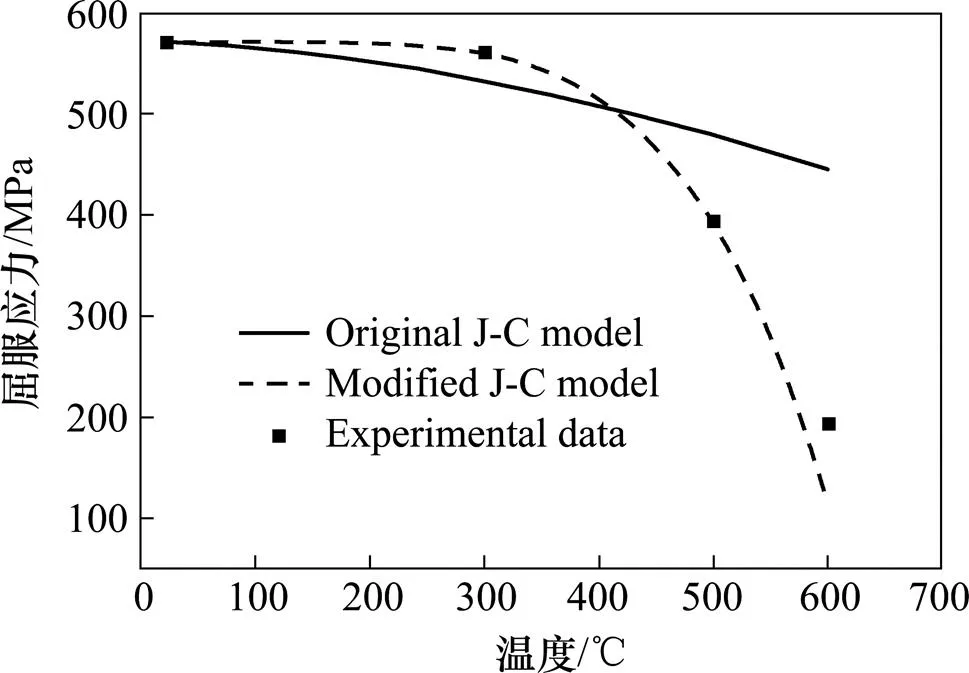
圖8 修正后不同溫度下屈服應力與實驗結果對比

3) 確定參數

根據室溫下不同應變率下的拉伸實驗可以確定本構模型中的應變率相關系數。高應變率加載會使試件在實驗過程中溫度升高，高應變率加載可以看作是一個絕熱過程，溫度的升高率可以通過式(10)計算

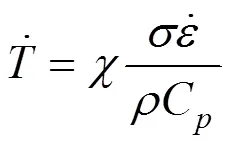
式中：和C分別為材料的密度和比熱容，這里假定和C都是常量，其值分別為7.85 g/cm3與0.46 J/(K·g)；χ為熱量轉換系數，對于金屬材料χ一般取0.9[21]。因此，溫度的增量可以通過式(11)計算

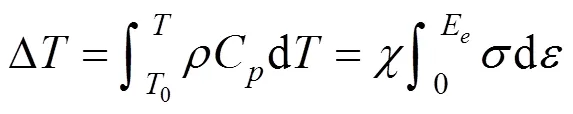
其中：為材料達到極限強度時的應變。根據公式計算，當應變率為500 s?1時Δ=10.87 K，應變率為1 500 s?1時Δ=12.35 K。可見高應變率絕熱效應對該材料的影響不明顯，為減少計算量可以忽略高應變率加載的溫度效應。

使用與確定參數同樣的線性擬合方法可以確定應變率相關系數，得到=0.010 9。

圖9中展示了材料在室溫下不同應變率拉伸的實驗結果與原始本構模型結果，通過對比發現，所得本構模型在低應變率(0.000 1 s?1~0.1 s?1)時與實驗結果吻合較好，在高應變率(500 s?1~1 500 s?1)下結果相差很大。

圖9 原J-C模型預測結果與實驗結果對比

通過觀察發現，在高應變率實驗中，實驗數據點分布趨勢規律與低應變率時不一致，這說明參數不僅與應變率相關，而且與材料的應變相關，的值與應變之間的關系見圖10。因此，可以看作應變和應變率的函數，表達式如下

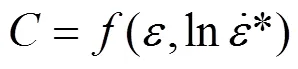
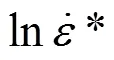
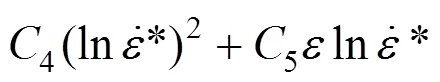
那么在室溫下J-C本構模型可以寫成

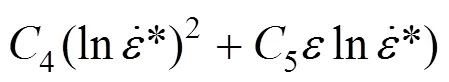
其中：0~5是需要求解的系數。參數和2個獨立變量之間的關系可以用三維空間中的曲面來 表示。

6個系數可以直接通過二元二次曲面擬合來確定，圖11為曲面擬合結果，實心曲面代表實驗結果，網格曲面為擬合曲面。修正后的J-C模型參數見表2。

3.2 模型誤差分析

圖12中對比室溫下不同應變率下拉伸實驗結果與修正后J-C本構模型預測結果，相比原始J-C本構模型，修正后的本構模型對刨削式吸能結構用45號鋼的動態力學行為有更好的預測能力。

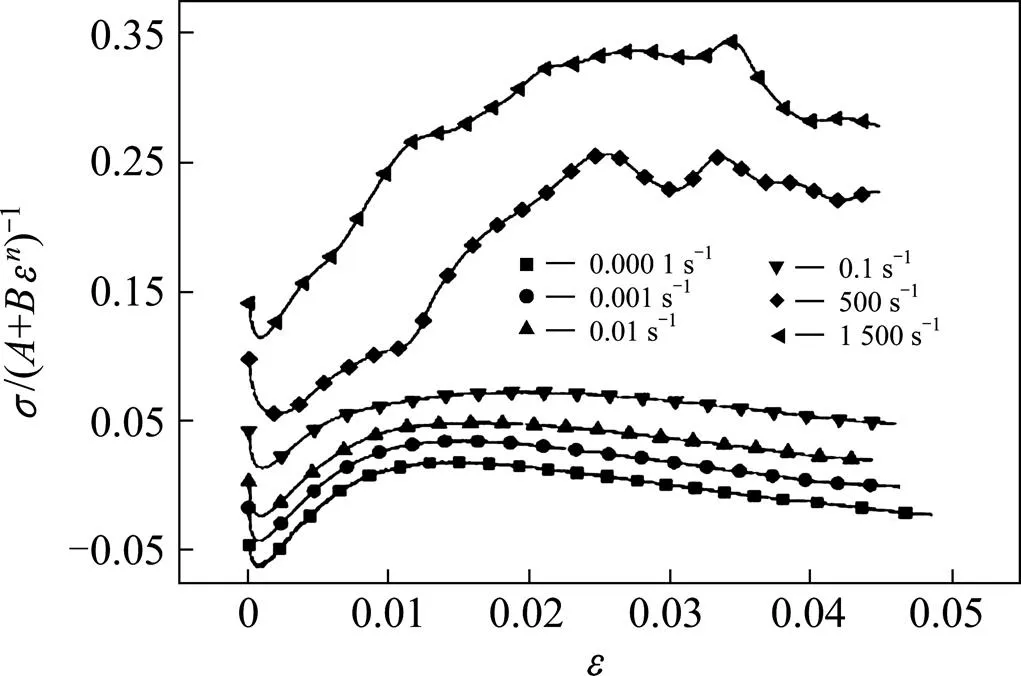
圖10 不同應變率下參數C與應變ε的關系曲線

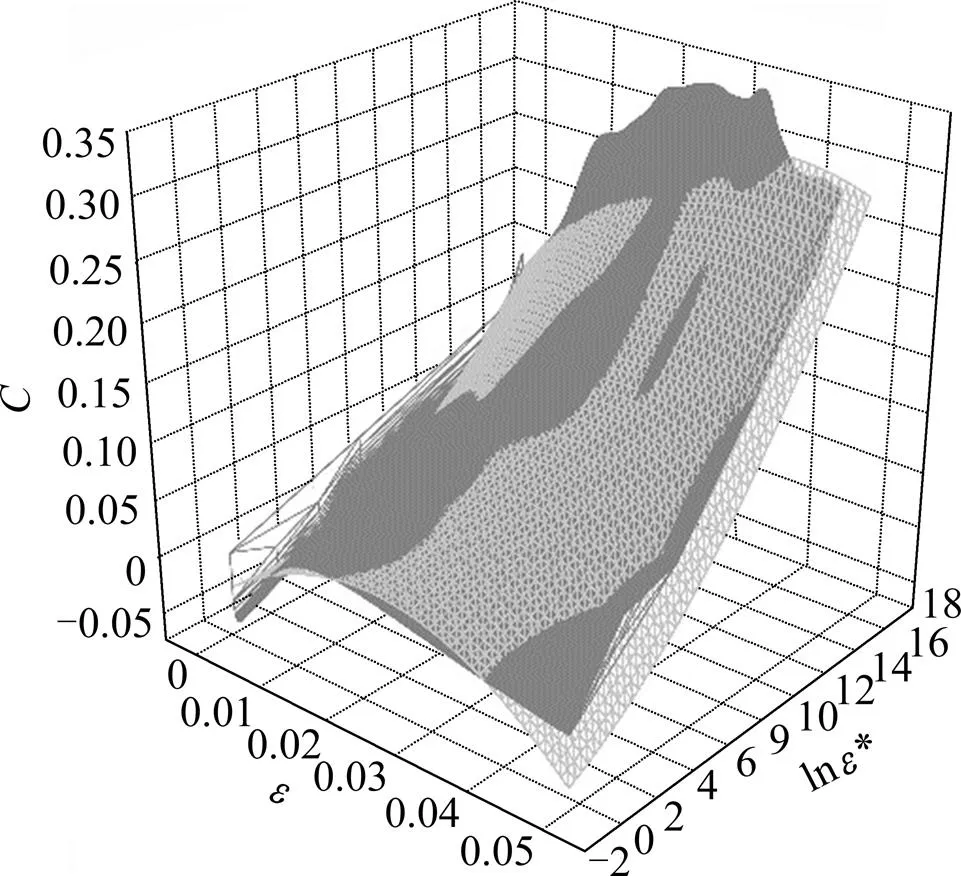
圖11 二元二次曲面擬合結果

表2 修正Johnson-Cook模型材料參數

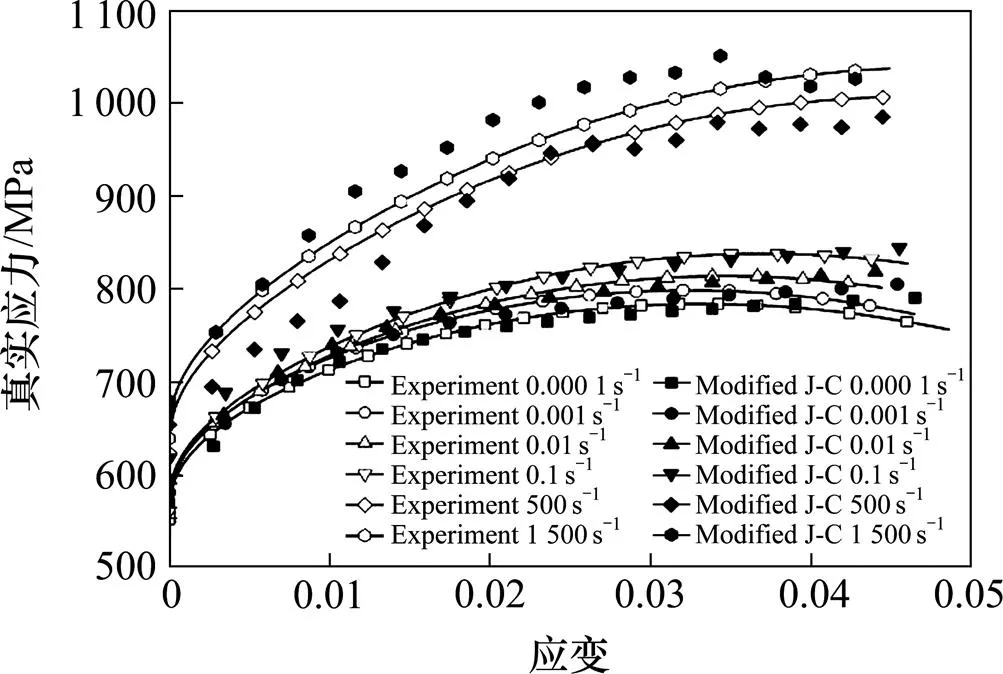
圖12 修正J-C模型預測結果與實驗結果對比

為了更準確地考察修正模型與原始模型對實驗結果的預測，本文對比3個誤差指標：相關系數、歸一化誤差均值和平均相對誤差絕對值，分別用，NMBE和AARE來表示，計算公式如下：

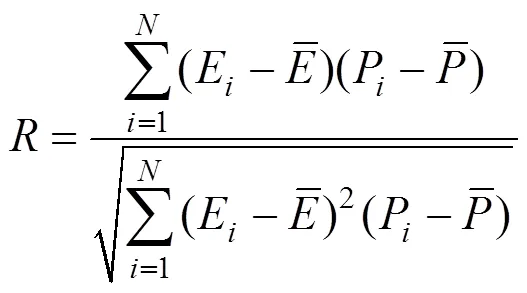
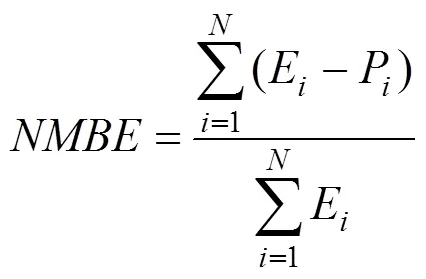
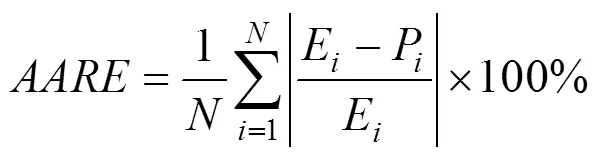
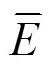
流變應力的實驗值和對應的本構模型的預測值展示在了圖13中，觀察對比結果可以看出，修正后數據點更接近最佳曲線，也就是說修正本構模型預測結果與實驗結果有更好的相關性。

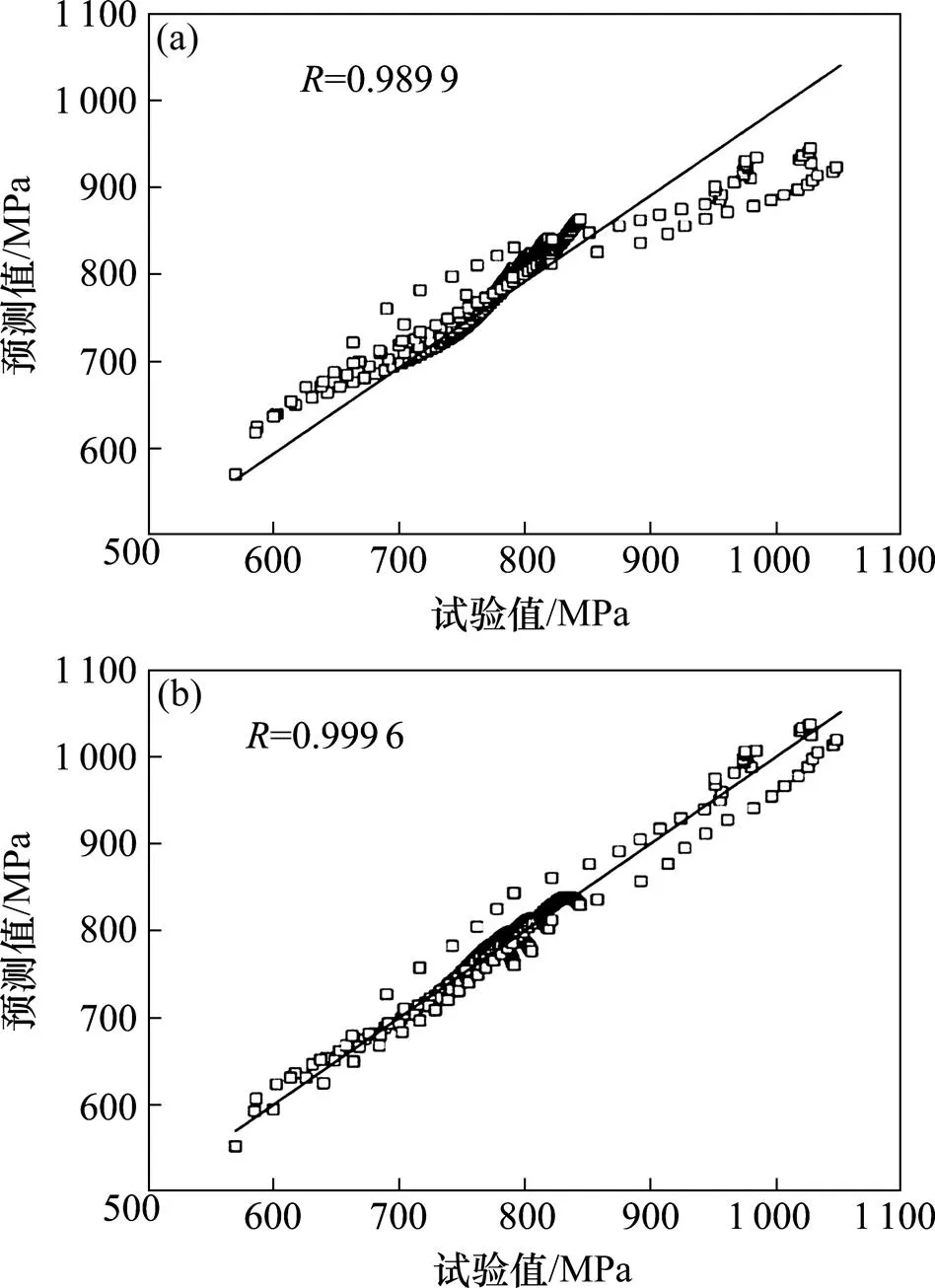
(a) 原始J-C模型；(b) 修正J-C模型

原始J-C模型與修正后J-C模型的誤差參數都列在表中。原始J-C模型的平均相對誤差絕對值為3.71%，經過修正降低至1.36%；原始J-C模型和修正后的J-C模型的歸一化偏差分別為0.60%和?0.008 8%。這些數據表明，修正后的J-C模型對流變應力的預測精度要高于原始J-C模型。

表3 原始J-C模型與修正J-C模型誤差指標對比

4 結論

1) 刨削式吸能結構用45號鋼為應力率敏感型金屬材料。隨著應變率提高，刨削式吸能結構用45號鋼在不同應變率下屈服強度及極限強度明顯 提高。

2) 基于實驗數據，對原Johnson-Cook模型的溫度軟化參數進行系數修正，引入函數對率敏感性參數進行二元二次多項式修正，得到了應變硬化與應變率耦合效應的Johnson-Cook修正模型。

3) 對比分析原J-C模型及修正J-C模型與不同應變率下拉伸的實驗結果的相關系數、歸一化誤差均值和平均相對誤差絕對值3個誤差指標，結果表明修正的J-C本構模型在預測不同應變率下的流動應力時有更高的精確度。

[1] 劉國偉, 夏茜, 王千葉, 等. 切削式吸能的慣性效應[J]. 交通運輸工程學報, 2015, 15(3): 62?70. LIU Guowei, XIA Xi, WANG Qianye, et al. Inertia effects of cutting energy absorption[J]. Journal of Traffic and Transportation Engineering, 2015, 15(3): 62?70.

[2] 常寧, 劉國偉. 軌道車輛切削式吸能過程仿真[J]. 中南大學學報(然科學版), 2010, 41(6): 2444?2450. CHANG Ning, LIU Guowei. Simulation for energy- absorbing process of railway vehicle in metal-cutting way[J]. Journal of Central South University (Science and Technology), 2010, 41(6): 2444?2450.

[3] 雷成, 肖守訥, 羅世輝. 軌道車輛切削式吸能裝置吸能特性研究[J]. 中國機械工程, 2013, 24(2): 263?267. LEI Cheng, XIAO Shoune, LUO Shihui. Research on energy absorption characteristics of rail vehicle energy- absorbing component in cutting way[J]. China Mechanical Engineering, 2013, 24(2): 263?267.

[4] 岳偉玲, 王喜順, 羅昌杰, 等. 圓孔拉刀式吸能器吸能特性的研究[J]. 機械設計與制造, 2014(7): 27?30. YUE Weiling, WANG Xishun, LUO Changjie, et al. Round broaching energy absorption characteristics of energy-absorbing device[J]. Machinery Design & Manufacture, 2014(7): 27?30.

[5] 董茹玲. 切削式吸能撞擊實驗系統設計及切削吸能特性研究[D]. 長沙: 中南大學, 2014. DONG Ruling. Design of the cutting energy-absorbing impact test system and research on the energy absorption characteristics of cutting energy-absorbing[D]. Changsha: Central South University, 2014.

[6] QIN J, CHEN R, WEN X, et al. Mechanical behaviour of dual-phase high-strength steel under high strain rate tensile loading[J]. Materials Science and Engineering: A, 2013, 586: 62?70.

[7] HU D Y, MENG K P, JIANG H L, et al. Strain rate dependent constitutive behavior investigation of AerMet 100 steel[J]. Materials & Design, 2015(87): 759?772.

[8] Singh N K, Cadoni E, Singha M K, et al. Dynamic tensile behavior of multi-phase high yield strength steel[J]. Materials & Design, 2011, 32(10): 5091?5098.

[9] Akbari Z, Mirzadeh H, Cabrera J M. A simple constitutive model for predicting flow stress of medium carbon microalloyed steel during hot deformation[J]. Materials & Design, 2015(77): 126?131.

[10] 李國和, 王敏杰. 淬硬45鋼在高溫, 高應變率下的動態力學性能及本構關系[J]. 爆炸與沖擊, 2010, 30(4): 433?438. LI Guohe, WANG Minjie. Dynamic mechanical properties and constitutive relationship of hardened steel (45HRC) under high temperature and high strain rate[J]. Explosion and Shock Wave, 2010, 30(4): 433?438.

[11] 林莉, 支旭東, 范鋒, 等. Q235B鋼Johnson-Cook 模型參數的確定[J]. 振動與沖擊, 2014, 33(9): 153?158. LIN Li, ZHI Xudong, FAN Feng, et al. Determination of parameters of Johnson-Cook models of Q235B steel[J]. Journal of Vibration and Shock, 2014, 33(9): 153?158.

[12] Singh N K, Cadoni E, Singha M K, et al. Quasi-static and dynamic tensile behavior of CP800 steel[J]. Mechanics of Advanced Materials and Structures, 2014, 21(7): 531? 537.

[13] Cowper G R, Symonds P S. Strain-hardening and strain-rate effects in the impact loading of cantilever beams[R]. Brown Univ Providence Ri, 1957.

[14] Johnson G R, Cook W H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures[J]. Engineering Fracture Mechanics, 1985, 21(1): 31?48.

[15] Gurson A L. Continuum theory of ductile rupture by void nucleation and growth: Part I—yield criteria and flow rules for porous ductile media[J]. Journal of Engineering Materials and Technology, 1977, 99(1): 2?15.

[16] Zerilli F J, Armstrong R W. Dislocation-mechanics-based constitutive relations for material dynamics calculations [J]. Journal of Applied Physics, 1987, 61(5): 1816?1825.

[17] Umbrello D, M’saoubi R, Outeiro J C. The influence of Johnson-Cook material constants on finite element simulation of machining of AISI 316L steel[J]. International Journal of Machine Tools and Manufacture, 2007, 47(3): 462?470.

[18] LIN Y C, CHEN X M, LIU G. A modified Johnson-Cook model for tensile behaviors of typical high-strength alloy steel[J]. Materials Science and Engineering: A, 2010, 527(26): 6980?6986.

[19] HE A, XIE G, ZHANG H, et al. A comparative study on Johnson-Cook, modified Johnson-Cook and Arrhenius- type constitutive models to predict the high temperature flow stress in 20CrMo alloy steel[J]. Materials & Design, 2013(52): 677?685.

[20] Bobbili R, Paman A, Madhu V. High strain rate tensile behavior of Al-4.8Cu-1.2Mg alloy[J]. Materials Science and Engineering: A, 2016(651): 753?762.

[21] B?rvik T, Hopperstad O S, Dey S, et al. Strength and ductility of weldox 460E steel at high strain rates, elevated temperatures and various stress triaxialities[J]. Engineering Fracture Mechanics, 2005, 72(7): 1071? 1087.

Investigation on the mechanical behavior and constitutive model of 45 steel used in planing energy-absorbing structure at high strain rate and high temperature

HE Xiaolei1, SI Zhiqiang1, CHEN Xuanzhen2, PENG Shan2, PENG Yong2, XU Ping2

(1. China Railway Rolling Stock Corporation Tangshan Company Limited, Tangshan 063000, China; 2. Key Laboratory of Traffic Safety on Track of Ministry of Education, School of Traffic & Transportation Engineering, Central South University, Changsha 410075, China)

In order to study the dynamic behavior of the 45 steel used in planning energy-absorbing structure under different strain rates at different temperature, this paper investigated the material by means of experiments and modeling. A series of tensile tests were conducted under different strain rates (10?4s?1to 1 500 s?1) and different temperature (300~600 ℃). The experimental results show that the material is rate-sensitive. The yield strength and ultimate strength increase with the increase of strain rate and decrease with the increase of temperature because of heat softening effect. Based on the experimental results, a Johnson-Cook constitutive model was proposed to depict dependence of flow stress on strain rate and temperature. In addition, the model was modified by modifying heat softening parameter and rate-sensitive parameter using linear and binary quadratic regression methods, respectively. Error analysis for the original and modified J-C model indicates that the model has high accuracy in predicting the flow stress at different strain rates.

45 steel; SHTB; constitutive relation; modified Johnson-Cook model

10.19713/j.cnki.43?1423/u.2019.01.029

U271.97

A

1672 ? 7029(2019)01 ? 0215 ? 08

2018?09?04

中車唐山機車車輛有限公司科技資助項目(2016YFB1200506)；湖南省自然科學基金青年資助項目(2015JJ3155)

彭勇(1984?)，男，湖南常德人，教授，博士，從事軌道交通醫學損傷研究；E?mail：yong_peng@csu.edu.cn

(編輯 蔣學東)