橡膠減振系統的動力學沖擊模擬和試驗

Robert Keqi Luo

?

橡膠減振系統的動力學沖擊模擬和試驗

Robert Keqi Luo1, 2

(1. Trelleborg Antivibration Solutions, Leicester LE4 2BN, UK; 2. 中南大學 土木工程學院，湖南 長沙 410075)

橡膠減振裝置在鐵道運輸系統中是必不可少的部件。基于將橡膠結構大變形和高阻尼特性考慮在內的自然頻率域(NFR-Natural Frequency Region)方法，針對實際工業減振產品CUS單元在整個沖擊過程中的動力響應測試，分別用2種模擬沖擊質量體的有限元模型(點質量模型和實體模型)進行較詳盡的分析，評估實體橡膠減振系統的時域沖擊響應，所模擬的結果和測試數據吻合良好。可為有關工作提供參考，有助于更準確地模擬橡膠減振系統的動力響應，從而加快和優化設計過程。

橡膠減振器；動力沖擊；橡膠阻尼；回彈能；自然頻率域

橡膠兼具良好的阻尼和彈性特性。由橡膠與金屬黏接而成的減振器在鐵路機車和車輛減振系統中起著關鍵作用；由橡膠制成的墊板在鐵道工程中亦是必不可少的減振元件。隨著高速鐵路的飛速發展，對橡膠減振器的研究也日趨活躍, 特別是以動力學為基礎的減振降噪領域。尋求有效的數值模擬方法來評估橡膠減振器的工作性能有重要意義。在動力學分析中，橡膠減振器的彈性通常被簡單地處理為一彈簧，阻尼特性則為一阻尼器[1?7]。Grassie[8]采用雙自由度集中質量模型研究橡膠墊板的動剛度特性。在分析由鐵路軌道不平順引起的鐵路車輛轉向架疲勞損傷中，均將橡膠減振系統在動力學模型中簡化為彈簧和阻尼器[9]；而在實體橡膠的動力學模擬中，黏彈性方法的Maxwell、Kelvin-Voigt、fractional Kelvin-Voigt等模型及其改進型受到更多關注[10?14]，Busfield等[15]用自由振動法測試天然填充橡膠的動彈性模量，發現預拉應變對其影響很小；SHI等[16]嘗試采用5個參數的一維彈簧模擬實體橡膠。然而，現有黏彈性方法在模擬的準確度和模型復雜性方面存在局限性[17]。另一方面，Rayleigh阻尼被廣泛應用于各種線性、非線性及復合材料的結構動力學模擬，亦用于鐵路車輛動力學研究和疲勞分析中；但遇到實體橡膠減振系統時，問題的復雜性就顯示出來。盡管Suarez等[18]通過PSD方法將彈性橡膠車輪與傳統鋼車輪在振動和噪音方面相比較，得出了橡膠車輪明顯優于鋼車輪的量化值;我們也在將Rayleigh阻尼引入實體橡膠減振系統的分析中作了一些前期工作[19?20]，取得了一定的進展。但整體上，由于橡膠材料的真實阻尼特性較復雜、且難以給予準確描述等原因，有關文獻在這方面的記載十分有限, Rayleigh阻尼在實體橡膠減振系統的時域動力學分析領域尚待更廣泛和深入的開展。本文從橡膠減振器的設計和應用角度出發，采用近年來為工程設計和計算而提出的自然頻率域 NFR (Natural Frequency Region) 方法, 對一工業研發產品進行動力學沖擊模擬分析，并與試驗數據對比, 為提高其減振能力給出依據, 同時測試NFR方法的可靠性，也為今后新型橡膠減振器的研發打下基礎。

1 橡膠減振器的動力學沖擊試驗

動力學沖擊試驗是用組合單元減振器(CUS)來進行的。該減振器由2個多向圓形減振器(Multi- Directional Snubbing ，簡稱 MDS)和一個不含液體的活塞圓形減振器(Circular Piston Mount，簡稱CPM)組成。單個MDS的高度約為50 mm，直徑約110 mm。單個CPM的高度約為80 mm，直徑約為130 mm。MDS用天然的填充橡膠，其剪切彈性模量約為0.7 MPa。CPM采用剪切彈性模量約為1.0 MPa的EPDM (三元乙丙) 橡膠。組裝時CUS的預壓縮長度約為10 mm(兩端的MDS各預壓5 mm)。

用于進行動力學沖擊試驗的平臺的主要部件示意于圖1。試件CUS 被固定在由框架支撐的平臺上。一圓桿將止撞塊與減振器相連。沖擊鋼塊用連接桿件固定并由一個電子開關來控制。在沖擊試驗中，啟動電子開關, 將鋼塊和連接桿件釋放, 使鋼塊打擊下面與CUS相連的止撞塊從而獲得所需的減振器的動力沖擊響應。沖擊過程中獲得的動力位移時程數據由固定于CUS上面的動力位移傳感器記錄并送入自動記錄設備。沖擊鋼塊連同相連桿件的質量約為250 kg。沖擊速度約為440 mm/s。圖2顯示的是CUS在沖擊作用下的位移?時程曲線。最大的沖擊位移約為7 mm，主響應頻率約為10 Hz。在3處回彈頂峰附近并伴有某些高頻反應成分。

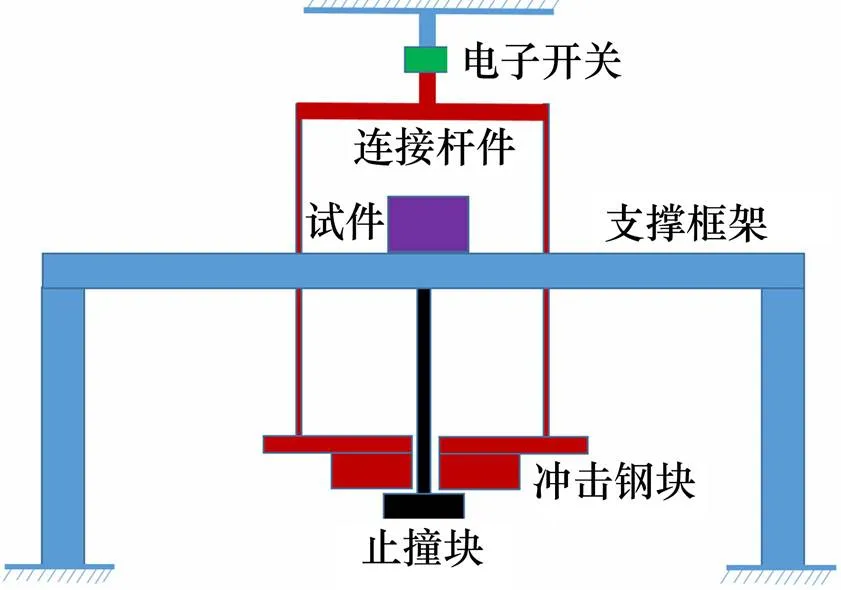
圖1 用于沖擊試驗的平臺示意圖

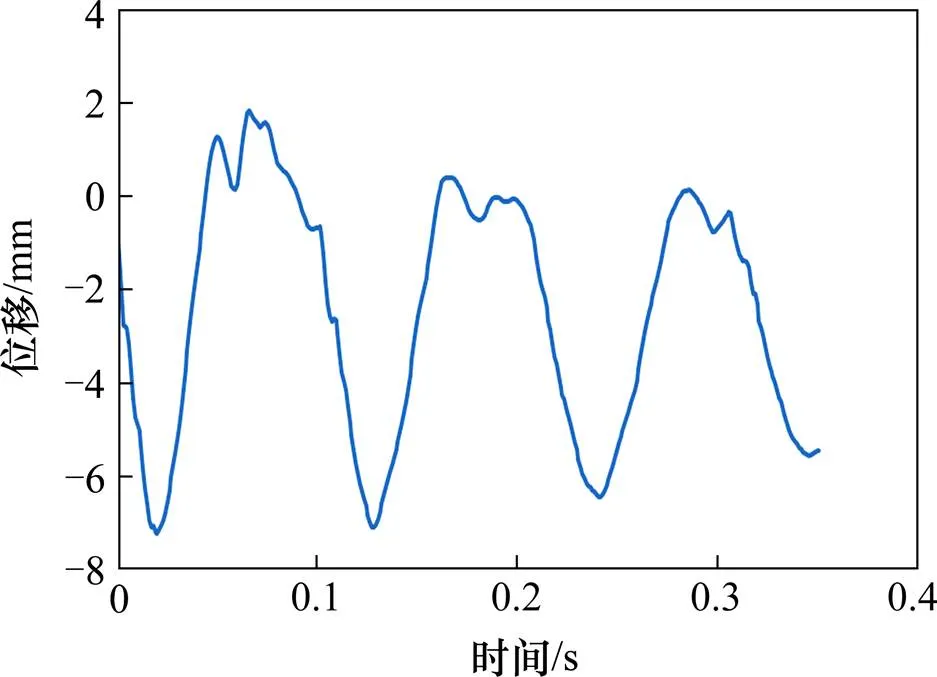
圖2 沖擊試驗得到的CUS位移?時間曲線

2 動力學方程和參數

動力學的通用方程組可寫為

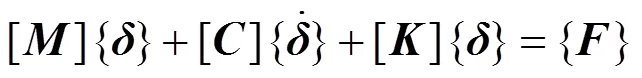
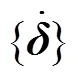
在進行動力外荷載分析之前，一般先對系統的自然振動頻率和振型進行分析。其主要目的是獲得和系統外力無關的自由振動頻率和振型，為減振部件的設計提供依據。同時也可用來確定系統的阻尼數值, 因為Rayleigh阻尼值的計算需要用到自然振動頻率。系統自由振動方程組可寫為

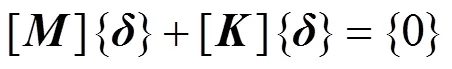
其中：{0}為0向量列陣。

在方程組(1)和(2)中，橡膠的彈性形成了部分剛度矩陣。現在廣泛應用的橡膠彈性模型是以應變能為基礎的[21?22]。其通用表達式為

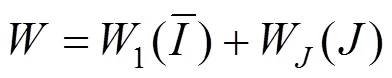
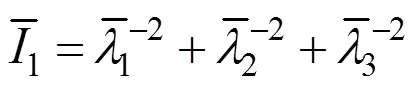
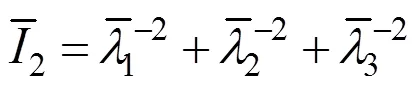
模擬中采用多項式的應變能表達式(=3)來計算減振器的彈性部分

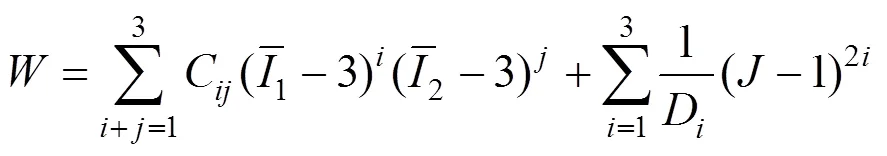
其中：C和D為材料參數，系以協作或合同形式從有關公司或大學采集、并經工業產品驗證其有效性和準確度。出于商業上的原因，具體的C數值這里沒有給出。C數值可以通過文中給出的剪切彈性模量獲得[20?22]。D數值為：

MDS所用的橡膠：D= 0.001 5

CPM所用的橡膠：D= 0.001

在方程組(1)中，阻尼矩陣主要由橡膠部分形成。橡膠的阻尼通常描述為在加載和卸載的過程中能量的損失，可以由回彈法[23?24]或其他方法獲得。對于回彈能的測試方法已經標準化，詳見文獻[24]。測試方法是使一個自由下落的鋼塊沖擊橡膠試件，回彈后記錄沖擊前和沖擊后的高度；計算沖擊前后的能量比值,此即為回彈比0以百分數表示。用于回彈能試驗的設備詳見文獻[20]。從減振原理來看，回彈能是橡膠的一種材料特性。最近的研究顯示，它在應力軟化和Mullin現象的描述中起著重要作用[20]。橡膠的阻尼比可以用式(7)表示[25]

根據Rayleigh 阻尼假設，阻尼矩陣可以用式(8)表達

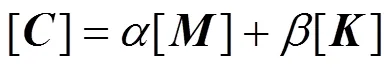
其中的參數和與自由振動頻率1和2及阻尼比有關，可以寫成式(9)：

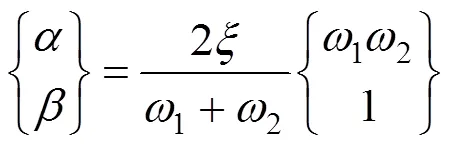
雖然從原理上來說，在所感興趣的范圍內選取自由振動頻率1和2都應該有效。但在實際工程應用中不同選擇值可能對應差別迥異的結果。工程實例研究發現，采用自然頻率域NFR方法傾向于獲得與實際應用更為接近的結果。該方法是基于對某橡膠減振系統的最大頻響為1 000 Hz時的動剛度試驗而建立的[26]。一個NFR定義為某系統自然頻率為主導的響應區間。為確定NFR，將兩對靠的最近的自然頻率值取均值，從而獲得該區的起終頻率。有一個例外，就是對第一個(基本) NFR,其起點頻率視為0，即準靜態點。每個NFR只含有一個主導的自然振動頻率，但該頻率不一定正好位于NFR的中位點。根據以上定義，可以把含有基本自然振動頻率的NFR稱為基本NFR或第一NFR；含有第2個自然振動頻率的NFR為第二NFR，依此類推。舉例來說：假設一橡膠減振系統的前三階自然振動的頻率依次為：200，600和900 Hz，則第一NFR的頻率區間為0~400 Hz，主導頻率為200 Hz；第二NFR的頻率區間為400~750 Hz，其主導頻率為600 Hz。就工程應用而言，計算阻尼參數選用頻率時，必須至少有一個其對應的振型與外力導致結構的變形相一致。此外，與一般線性材料組成的小變形結構不同，橡膠結構是一個大的變形系統，特定主導振型很容易產生除主導方向以外其他方向上的分量；當它們足夠大時，其效應不宜被忽略。這意味著如果在實際動力響應中除主導振動頻率外還有其他高頻分量存在，則需要考慮相鄰自然振動頻率和振型在其主導方向外可能產生的影響。

3 有限單元模型

考慮到不同工況，用Abaqus軟件[21]建立相應的有限元模型。對自然頻率分析來說，有必要對CUS單元建立一個完整的模型，見圖3。該模型將沖擊質量塊，連接桿件和止撞塊等簡化為一集中質量。當進行沿豎直方向的動力學沖擊模擬時，利用結構與荷載的對稱性，采用1/4模型，見圖4。材料有鋼和橡膠2種，橡膠還進一步分成用于MDS的天然填充材料和用于CPM的EPDM。鋼材料用標準塊狀單元(C3D8)，橡膠材料用超彈性單元 (C3D8H) 來模擬．用于自由振動分析所需的自由度約為65萬個，用于動力學沖擊的自由度約為38 萬個。

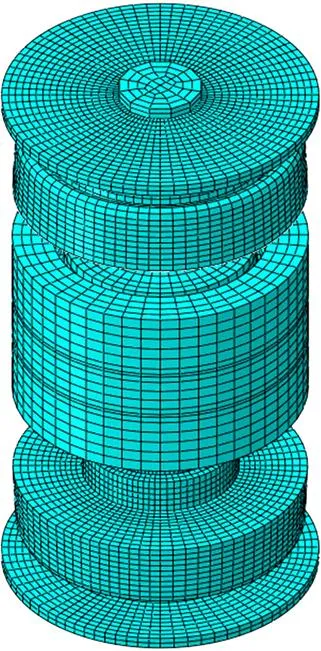
圖3 用于自然頻率評估的CUS單元的有限元模型

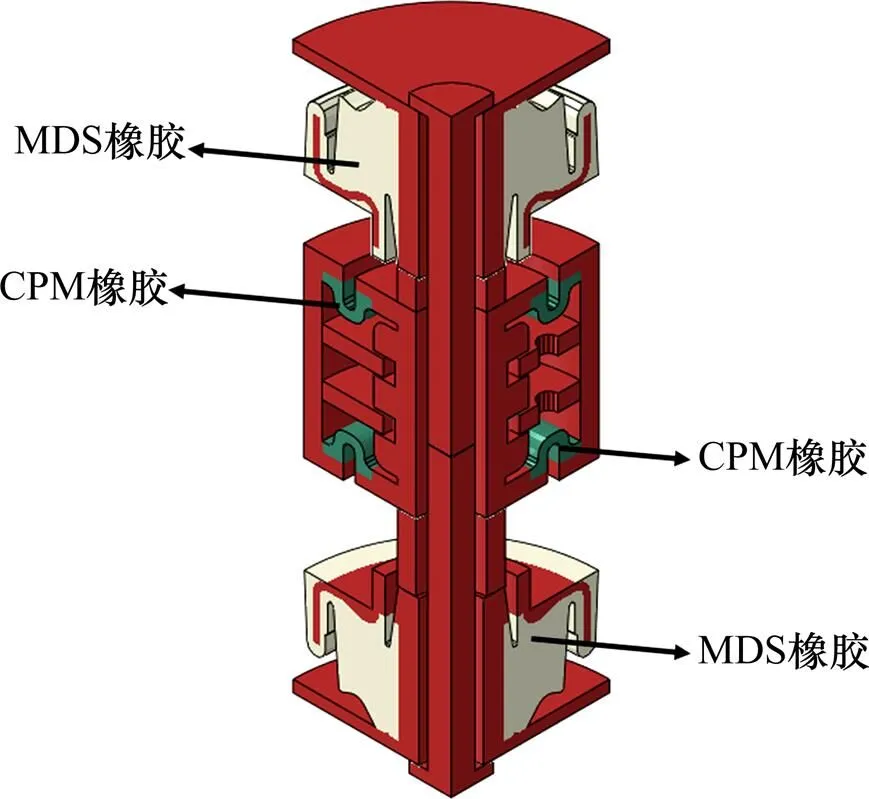
圖4 用于動力學沖擊試驗評估的CUS單元的有限元模型 (為清晰起見，已去網格，未標部分為金屬件)

4 結果和討論

4.1 自然頻率和阻尼

從自然頻率分析中得知，CUS單元的基頻約為10 Hz；其振型為豎向振型, 如圖5(a)所示。很明顯，豎向位移在該振型中起主導作用。接下來的自由振動頻率約為65 Hz，其振型為2塊鋼圓板在水平方向的輻射變形，見圖5 (b)。圖5(c)和5(d)是中間螺栓沿2個不同方向的彎曲振型，對應于同一頻率，也約為65 Hz(共軛)。由于動力學沖擊試驗沿豎直方向進行的，根據NFR方法可直接選取豎向振型頻率1=10 Hz。選擇第2個自然頻率時則需要查看另外3個振型在豎直方向的分量。在自由振動頻率和振型分析中，經過正交轉換后的最大相對位移值為1。在水平振型中，其豎向位移分量小于0.002，而另2個振型卻高達0.27。因此, 水平振型可以舍棄，但2個共軛振型的豎向位移分量均須納入，據此確定2=65 Hz來計算本案例中橡膠的阻尼參數。對MDS和CPM的橡膠材料進行了相應的回彈能試驗，所獲得的回彈能比值分別約為75%和40%。從而得到的相應橡膠阻尼參數值是：

MDS所用的橡膠：=0.35，=0.000 53

CPM所用的橡膠：=0.82，=0.001 3

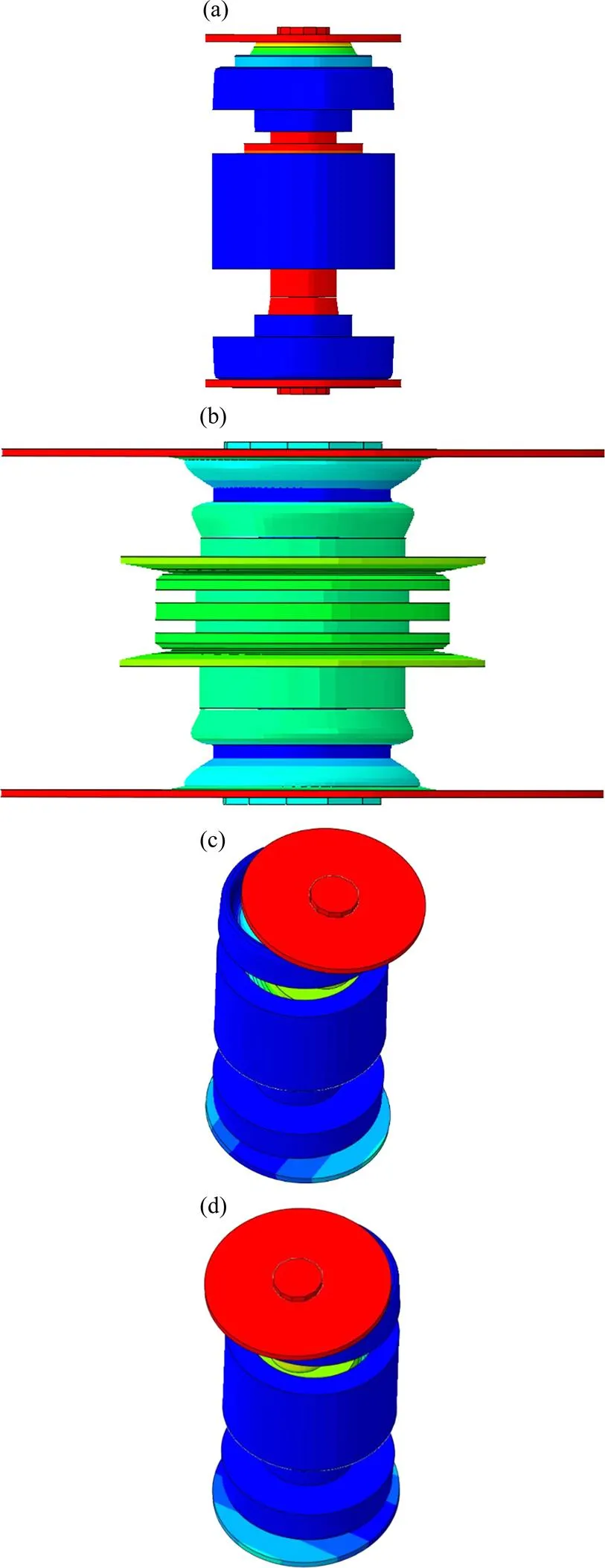
(a) 豎向振型：9.97 Hz；(b) 水平振型：64.68 Hz；(c) 彎曲振型1：64.79 Hz；(d) 彎曲振型2：64.79 Hz

4.2 點質量模擬沖擊鋼塊時的動力學結果

采用圖4中的有限元模型來模擬對CUS單元所做的沖擊試驗。計算時假設在沖擊過程中, 沖撞質量始終不脫離止撞塊; 其依據是沖撞塊上附加了一個放反彈裝置 (約有1.5 mm的回彈間距) 。為選擇合適的時間步長以保證結果的準確性，分別用最大步長為1 ms和0.5 ms做了模擬對比。發現兩者幾乎沒有差異。故此，選定最大步長為0.5 ms。圖6 給出了點質量模擬得到的沖擊力時程曲線。從曲線上看，最大沖擊峰值約為22.8 kN，發生的時間大約在20 ms。

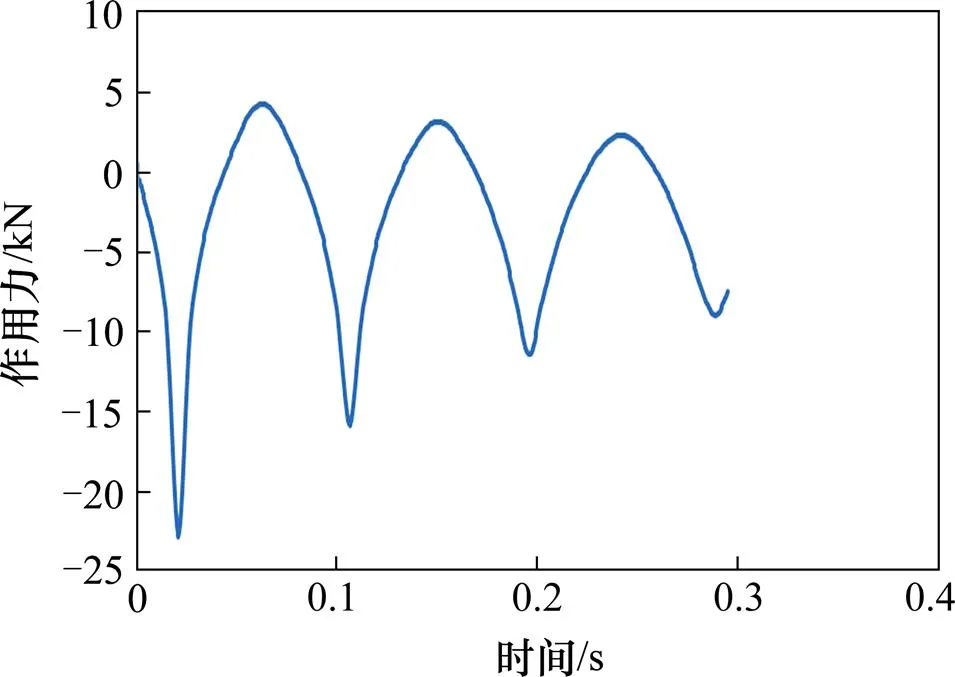
圖6　點質量模擬沖擊鋼塊時得到的沖擊力時程曲線

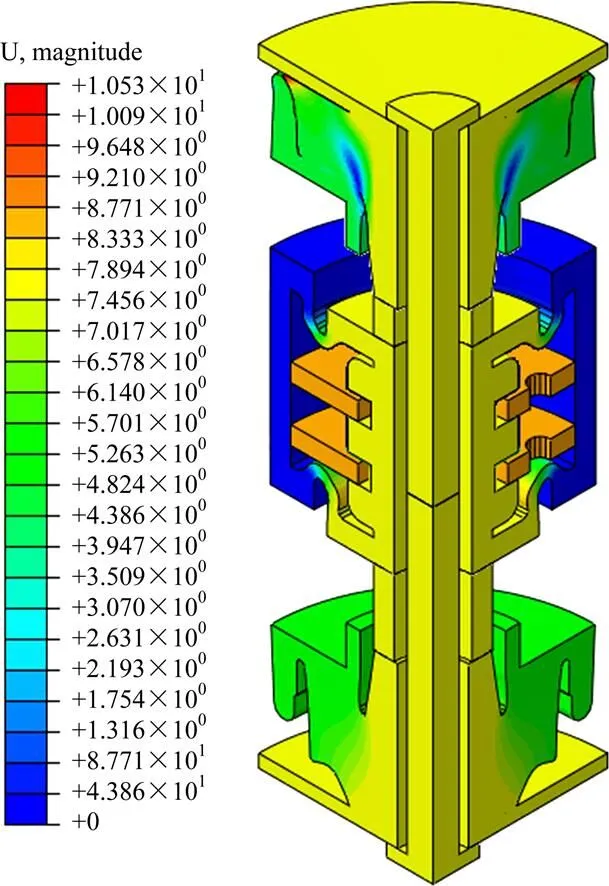
單位：mm

圖7顯示了在最大沖擊力下的CSU變形圖，最大絕對位移(含豎向和水平方向的位移)發生在MDS頂端的橡膠材料中，其值約為11 mm。在第1個沖擊峰值過后，系統進入到自由振動狀態并開始回彈。至約65 ms，回彈幅值達到最大，約為4.2 kN。此時的反彈變形圖可見圖8。圖9顯示了模擬的反應曲線和測試值的對比結果。從圖9可見，模擬反應曲線沿沖擊方向的幅值和試驗值大致相符，但回彈方向相差較大。過完第1個反彈峰后，時間差異逐漸開始加大。模擬曲線很平滑，在前3個回彈峰值上沒有任何高頻成分。故此，試驗曲線上的高頻干擾是真實的沖擊響應還是環境噪聲以及時間差的問題，還有待進一步的分析。

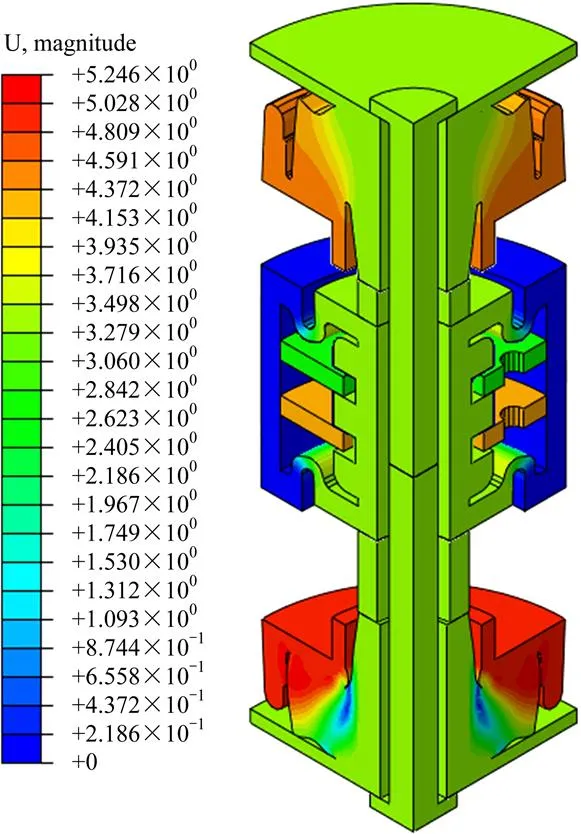
單位：mm

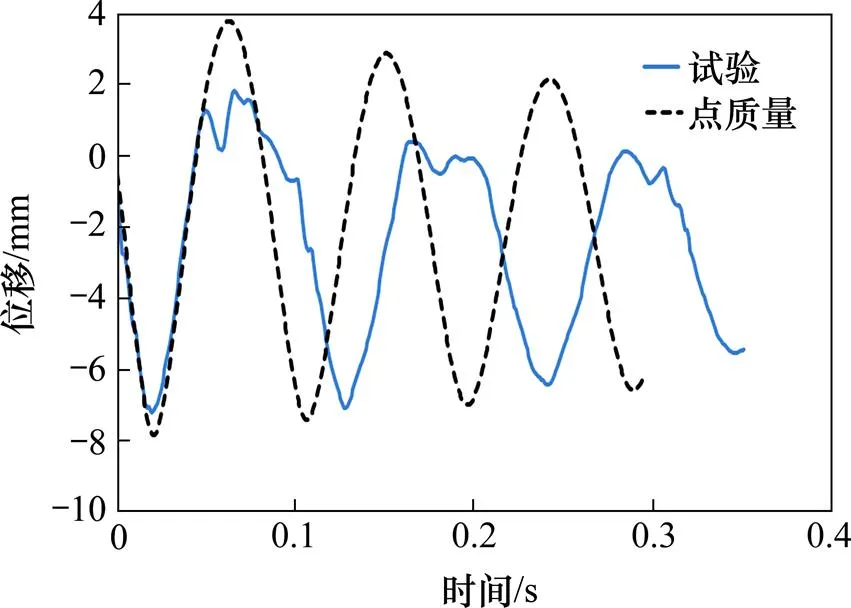
圖9　點質量模擬沖擊鋼塊時得到的沖擊位移時程曲線和測試值得對比

4.3 有限元實體模擬沖擊鋼塊時的動力學結果

為查明引起高頻分量和時間差的原因，考慮到沖擊質量塊是由鋼制成，它有彈性也有相當的尺寸且附帶的防回彈機構有間距存在。這個防回彈結構也是原來做集中質量塊處理的依據，因為在前面假設了沖擊后沖撞質量塊和止撞塊不會有相對運動。現在，另加入1個包含沖擊質量塊，連接鋼桿，止撞塊和防回彈結構在內的有限元模型。這個沖擊質量塊是一圓形的環狀，整個厚度約為145 mm，最大直徑約為700 mm。新的有限元附加模型示于圖10。圖11顯示了模擬給出的防反彈塊起作用時的狀況。這時的止撞塊在反彈至第1個峰后開始回落，而此時的沖擊質量塊仍在反彈時段；使得防反彈塊的上表面與止撞塊的下表面相接觸，形成了瞬時的反彈沖擊，從而使止撞塊停止下落而繼續反彈。如此反復，使沖擊質量塊與止撞塊之間多次來回接觸，導致了沖擊高頻分量的產生。這就合理地解釋了圖2 所示的試驗曲線反彈時出現多個高頻峰的原因。圖12給出了由有限元實際模擬質量塊體得到的沖擊力時程曲線圖。從圖12可見，其沖擊峰值減小為19.5 kN，為用點質量模擬沖擊質量塊時所得峰值的 85%。第一回彈峰值為2.2 kN，約為原來的一半。這說明沖擊質量塊與止撞塊之間多次來回接觸，不僅導致了沖擊高頻分量的產生，也造成了額外的能量消耗。圖13給出了位移時程模擬曲線和測試值的對比。結果顯示，兩者無論是響應幅值還是響應時間，模擬結果和實測值都很接近了。因此，實際狀況處理和模擬得當，選用合適的分析方法，結合仔細考量能夠得到可靠的結果，為橡膠減振系統設計提供保障和依據。

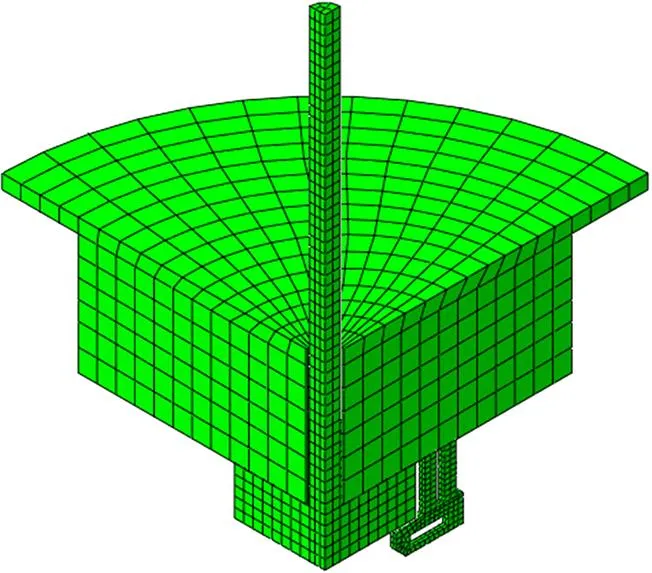
圖10　有限元實體模擬質量塊時的附加部分

圖11　反彈時防反彈塊體與止撞塊的接觸狀況

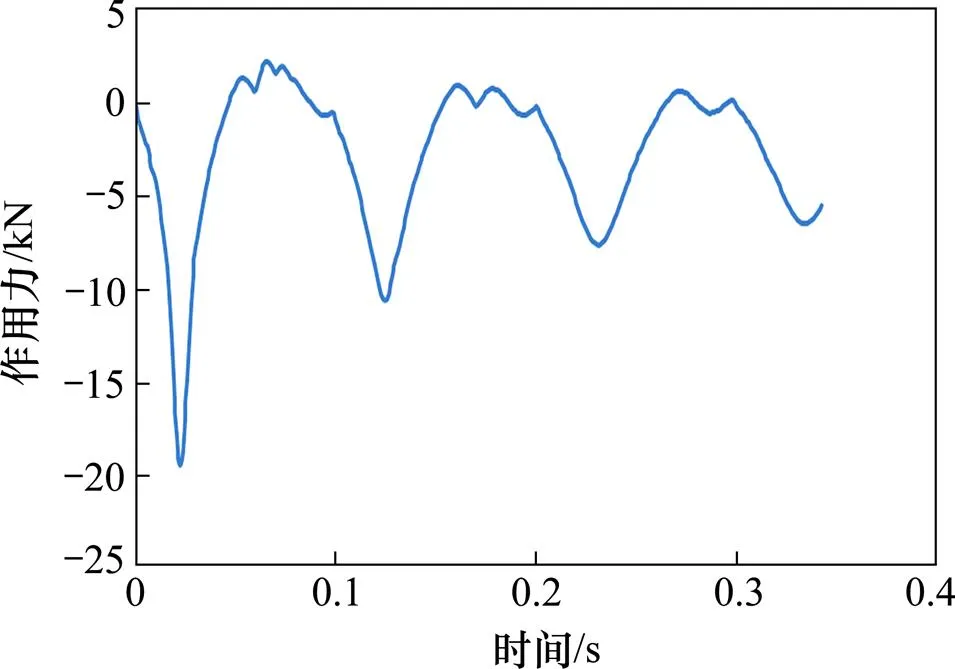
圖12　有限元實體模擬質量塊得到的沖擊力時程曲線

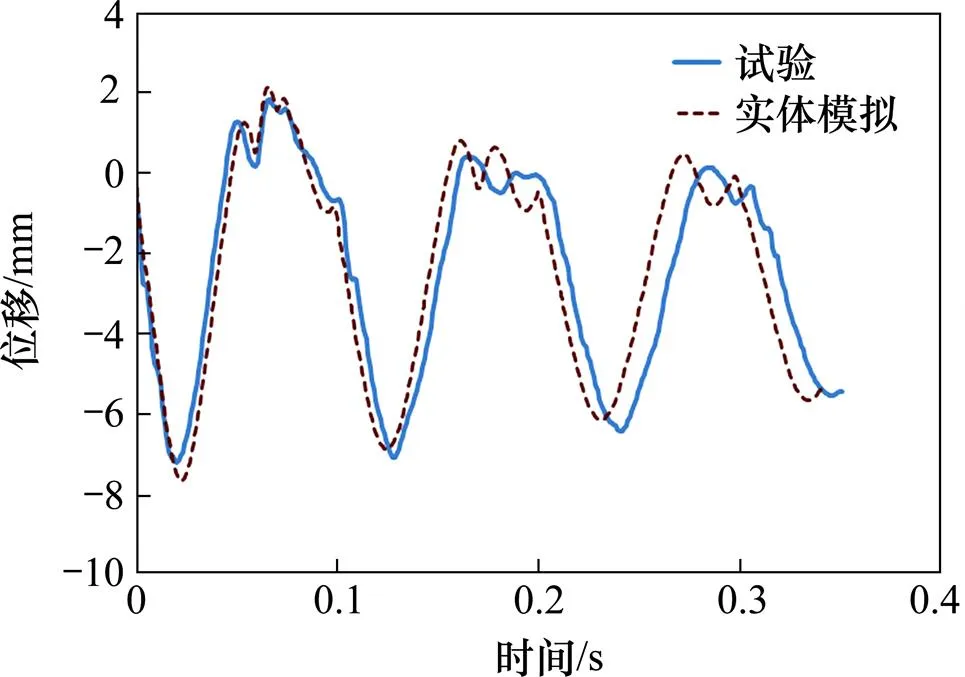
圖13 有限元實體模擬質量塊得到的沖擊位移時程曲線和測試值的對比

5 結論

1) 該案例成功地運用NFR方法將Rayleigh 阻尼引入到了橡膠減振系統的動力學沖擊分析中。針對實際工業減振產品CUS單元在整個沖擊過程中的動力響應測試，分別用2種模擬沖擊鋼塊的有限元模型(點質量模型和實體模型)進行了較詳盡的分析，所采用的NFR方法考慮了橡膠結構大變形和高阻尼的特性，較合理地給出了選取阻尼值的參考原則。

2) 模擬計算結果和測試數據對比發現，點質量模型的結果未能在反彈峰上呈現測試中的高頻分量，且響應時間差距較大；而在實體模型中，由于將沖擊界面變化納入了計算過程，結果顯示反應曲線和測試曲線高度貼合，解決了響應時間差的問題，并因此證實了高頻成分確為真實的結構響應而非環境噪聲。

3) 本文采用的NFR法符合工程原理，不僅獲得了較黏彈性方法見于文獻報道的更理想的模擬響應曲線，還避免了為確定黏彈性模型參數而需進行的復雜的數值擬合計算，從而減少了不同模型之間的計算誤差，是一種較好的動力學數值模擬 方法。

4) Rayleigh 阻尼已被廣泛地用于工程結構動力學研究中，通過NFR方法將其引入大變形和高阻尼的橡膠減振系統更易于為工程技術人員掌握。本文可為有關工作提供參考，有助于更準確地模擬橡膠減振系統的動力響應，從而加快和優化設計 過程。

[1] Luo R K, Gabbitas B L, Brickle B V. An integrated dynamic simulation of metro vehicles in a real operating environment[J]. Veh Syst Dyn, 1994(23): 334?345.

[2] Berg M. A model for rubber springs in the dynamic analysis of rail vehicles[J]. J Rail and Rapid Transit, 1997(211): 97–108.

[3] Kari L. Audible-frequency stiffness of a primary suspension isolator on a high-speed tilting bogie[J]. Rail and Rapid Transit, 2003(217): 47?62.

[4] Jeon S. Roadbed bearing capacity and deformations in a conventional and an improved turnout system[J]. J Rail and Rapid Transit, 2016, 230(1): 97?102.

[5] 姜洪源, 敖宏瑞, 李瑰賢, 等. 金屬橡膠隔振器動力學模型與分析[J]. 湖南科技大學學報(自然科學版), 2004, 19(3): 23?27. JIANG Hongyuan, AO Hongrui, LI Guixian, et al. Modeling and analysis of dynamic characteristics of metal rubber isolator[J]. Journal of Hunan University of Science and Technology (Natural Science Edition), 2004, 19(3): 23?27.

[6] 鄧吉宏, 王軻, 陳國平, 等. 金屬橡膠減振器用于發動機安裝減振的研究[J]. 航空學報, 2008, 29(6): 1581? 1585. DENG Jihong, WANG Ke, CHEN Guoping, et al. Study on effect of engine installation metal rubber damper[J]. Journal of Aeronautics and Astronautics, 2008, 29(6): 1581?1585.

[7] 潘開名, 劉斌, 劉之洋, 等. 疊層橡膠支座隔震結構地基?結構動力相互作用分析[J]. 東北大學學報(自然科學版), 2002, 23(1): 71?74. PAN Kaiming, LIU Bin, LIU Zhiyang, et al. Laminated rubber bearing isolation structure foundation-structure[J]. Journal of Northeastern University (Natural Science Edition), 2002, 23(1): 71?74.

[8] Grassie S L. Resilient rail pads their dynamic behaviour in the laboratory and on track[J]. Proc Inst Mech Eng, 2007(203): 25?32.

[9] Luo R K, Gabbitas B L, Brickle B V. Fatigue design in railway vehicle bogies based on dynamic simulation[J]. Veh Syst Dyn, 1996, 25(Suppl): 438?449.

[10] Gil-Negrete N, Vinolas J, Kari L. Dynamic stiffness prediction of filled rubber mounts: comparison between a fractional derivative viscoelastic-elastoplastic model and a simplified procedure[C]// Austrell P-E, Kari L (Eds.), Constitutive Models for Rubber IV, A. A. Balkema, Rotterdam, The Netherlands, 2005: 479?485.

[11] Oh J S, Kim D Y, Kim T H, et al. Numerical prediction of the viscoelastic deformation of seat foam in response to long-term driving[J]. J Automobile Engineering, 2015, 229(2): 214?225.

[12] Na S D, Yoo W S. Improvement in the dynamic responses of the semi empirical vehicle model using the Maxwell force model for the suspension forces[J]. J Automobile Engineering, 2015, 229(14): 1996?2006.

[13] Bruni S, Collina A. Modelling the viscoelastic behaviour of elastomeric components: An application to the simulation of train-track interaction[J]. Veh Syst Dyn, 2000, 34(4): 283?301.

[14] Cervello S, Donzella G, Pola A, et al. Analysis and design of a low-noise railway wheel[J]. J Rail and Rapid Transit, 2001, 215(3): 179?192.

[15] Busfield J J C, Deeprasertkul C, Thomas A G. Effect of liquids on the dynamic properties of carbon black filled natural rubber as a function of pre-strain[C]// Dorfmann A, Muhr A (Eds.), Constitutive Models for Rubber, A.A. Balkema, Rotterdam, The Netherlands, 1999: 87?93.

[16] SHI H, WU P. A nonlinear rubber spring model containing fractional derivatives for use in railroad vehicle dynamic analysis[J]. J Rail and Rapid Transit. 2016, 230(7): 1745?1759.

[17] Tarrago M J, Gil-Negrete N, Vinolas J. Viscoelastic models for rubber mounts: Influence on the dynamic behaviour of an elastomeric isolated system[J]. Int J Veh Des, 2009, 49(4): 303?317.

[18] Suarez B, Chover J A, Rodriguez P, et al. Effectiveness of resilient wheels in reducing noise and vibrations[J]. J Rail and Rapid Transit. 2011, 225(6): 545?565.

[19] Luo R K. Impact simulation and experiment on rubber anti-vibration systems[J]. Polymer Testing, 2016(50): 335?342.

[20] Luo Robert Keqi. Numerical prediction & case validation for rubber anti-vibration system[M]. Germany: Lambert Academic Publishing, 2017.

[21] Dassault Systems. Abaqus user manual[M]. Dassault Systems, USA, 2018.

[22] Ogden R W. Non-linear elastic deformations[M]. Ellis Horwood, Chichester, UK. 1984.

[23] Nagdi K. Rubber as an engineering material: Guideline for users[M]. Germany: Hanser Publishers, 1993.

[24] BS ISO 4662: 2009. Rubber, vulcanized or thermoplastic. Determination of rebound resilience[S].

[25] Clough R W, Penzien J. Dynamics of structures[M]. McGraw-Hill, Inc, 1993.

[26] Luo Robert Keqi, GUO Naizheng, CHEN Xianmai. NFR (Natural Frequency Region) approach for dynamic evaluation of anti-vibration systems with rebound resilience method[J]. Polymer Testing, 2017(57): 288? 295.

Dynamic impact simulation and experiment of rubber antivibration system

Robert Keqi Luo1, 2

(1. Trelleborg Antivibration Solutions, Leicester LE4 2BN, UK; 2. School of Civil Engineering, Central South University, Changsha 410075, China)

Rubber antivibration devices are an essential part of the railway transportation system. Based on the NFR (NFR-Natural Frequency Region) method that takes into account the large deformation and high damping characteristics of rubber structures, and in the reference of the experiment of the dynamic response on the actual industrial antivibration product CUS unit during the entire impact process, detailed analyses have been performed using two finite element models of the impact mass (point mass model and solid model). The impact response of the solid rubber antivibration system has been successfully evaluated in the time-domain. The simulated results are in good agreement with the experimental data. This article may provide a reference for the relevant work and help to more accurately simulate the dynamic response of the rubber antivibration system so that a design process can be accelerated and optimized.

rubber antivibration component; dynamic impact; rubber damping; rebound resilience; natural frequency region

10.19713/j.cnki.43?1423/u.2019.01.026

U266

A

1672 ? 7029(2019)01 ? 0192 ? 08

2018?05?03

Robert Keqi Luo(羅克奇)(1956?)，男，北京人，高級工程師，博士，從事橡膠減振領域的研究；E?mail：Robert.luo@trelleborg.com

(編輯 蔣學東)