基于SVM-PSO算法的大跨度懸索橋撓度可靠度研究

鄧海波，常柱剛，李胡濤，張紅顯

?

基于SVM-PSO算法的大跨度懸索橋撓度可靠度研究

鄧海波1，常柱剛1，李胡濤2，張紅顯1

(1. 長沙市規劃設計院有限責任公司，湖南 長沙 410007；2. 林同棪國際工程咨詢(中國)有限公司，重慶 404100)

為了研究高維隨機參數作用下大跨度懸索橋運營階段撓度可靠度，在有限元計算基礎上，基于支持向量機(support vector machine，SVM)建立成橋階段撓度可靠度模型，結合優化后的粒子群算法(Particle Swarm Optimization，PSO)計算結構運營階段撓度可靠指標。研究結果表明：借鑒遺傳算法中的變異思想，通過設置中間變量約束條件，可以解決粒子群算法易早熟、后期迭代效率低的問題，進而提高計算效率與精度，基于SVM-PSO算法的結構可靠度方法高效準確，普立特大橋撓度可靠度滿足正常使用極限條件下的要求。

支持向量機；粒子群算法；可靠度；撓度；有限元法

懸索橋是目前跨越能力最大的橋型，是由主纜、加勁梁、吊桿、主塔和錨碇等組成的空間結構體系，結構變形控制難度較大。考慮各構件受材料性能、結構幾何參數、荷載作用效應、計算模式準確程度等多方面的綜合作用，實際建成的結構運營狀態下的位移必定會與設計有一定差異[1]。李廣奇等[2]利用BP神經網絡響應面法，對大跨度懸索橋進行靜力可靠度，驗證神經網絡響應面法的有效性。余曉琳[3]基于均勻設計和支持向量機的響應面法，計算懸索橋正常使用階段靜力可靠度。AN等[4]基于有限元分析法，考慮結構幾何非線性，計算懸索外荷載作用下的應力、位移解析解，并使用一階可靠度分析方法與蒙特卡洛法分析纜索結構靜力可靠性。李建慧等[5]利用拉丁超立方抽樣法選取樣本點，建立樣本點對應的神經網絡，基于重要抽樣蒙特卡羅法進行復雜結構的靜力隨機分析及正常使用階段可靠性分析。然而，懸索橋運營狀態下，結構位移是控制結構安全的重要參數，成橋階段隨機變量較多，采用傳統的可靠度計算方法，如JC法，當結構功能函數非線性較高時，往往難以收斂，蒙特卡洛法通過大量的迭代求解結構失效概率，計算效率較低，往往用于驗證計算精度，同時，神經網絡在擬合小樣本、高維度隨機變量響應面時，容易陷入局部最優的問題。支持向量機具有優秀的小樣本、高維度數據處理能力，基于結構風險最小化原則，不會產生過擬合現象，粒子群算法從隨機解出發，通過不斷搜索、迭代，進而尋找最優解，具有概念清晰、簡單易懂和收斂速度快等優點，因此，本文結合SVM與PSO特點，提出基于SVM-PSO算法的結構可靠度計算方法，并通過算例驗證該方法的計算精度，最后，以主跨628 m普立特大橋為研究對象，計算懸索橋正常運營狀態下標高控制可靠指標，完成該橋成橋階段標高控制可靠度分析。

1 SVM-PSO算法

1.1 SVM基本理論

支持向量機是在統計學習理論基礎上，于1995年由Vapnik V. N 提出的一種新型的機器學習方法[6]。和分別表示輸入樣本與輸出樣本，其中，表示對應的響應函數，為維向量，=[1,2,3,…x]。令分類函數()=T+，最優分類面問題轉化為如下約束優化問題

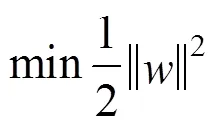
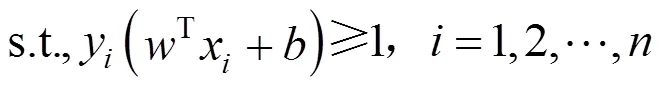
利用拉格朗日函數，求解以上函數對偶問題，引入拉格朗日因子可將上式轉化為

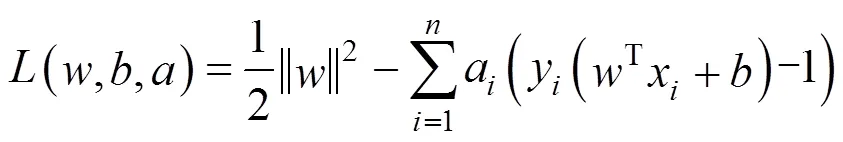
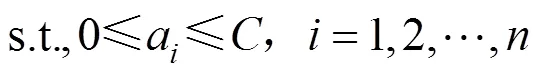
式中：>0為罰參數，以上是一個二次函數尋優問題，故根據式(3)可以求得解析解。根據以上分類間隔的定義可知，只有少部分點求解出的a為非0常數，其余樣本點代入上式求解a為0，這里提到的少部分點即為支持向量。

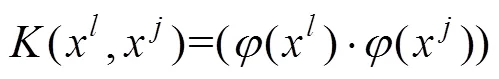
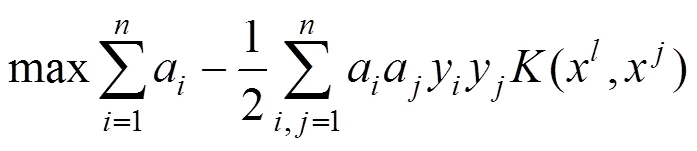
(4)

目前，具有廣泛適用性的核函數有線性核函數，徑向基核函數(RBF)，多項式核函數，sigmoid核函數。由于RBF是一個普遍使用且回歸、分類較好的核函數[7]，可調節的參數只有一個，同時適用于任意分布的樣本，完全滿足可靠度的計算分析，因此，本文選取徑向基核函數來構造SVM模型，SVM結構示意圖見圖1。

SVM模型性能受所選參數的影響，因此，參數和直接影響SVM模型的建立，所以在訓練SVM模型之前，需對SVM參數進行選擇。本文采用遺傳算法對SVM模型參數進行優化。

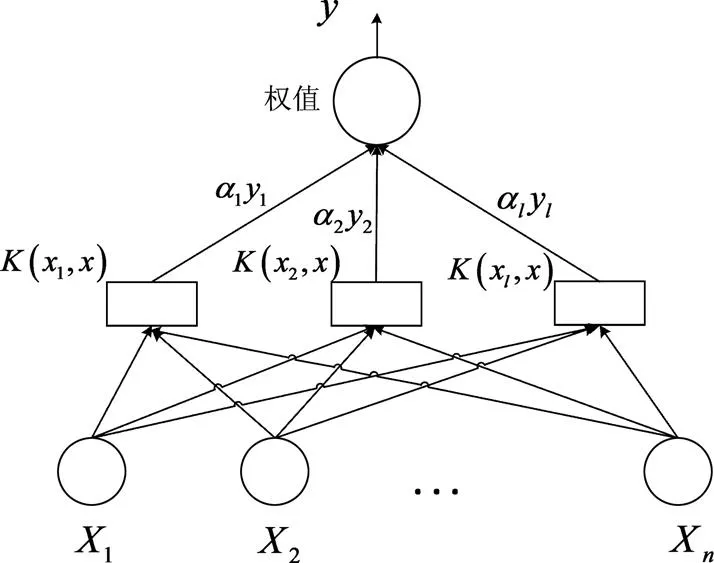
圖1 SVM結構示意圖

1.2 PSO算法優化

PSO算法是科研工作者受鳥群捕食行為啟發而提出的一張新型智能算法，在PSO算法中，每只鳥用粒子來表示，在距離食物最近的粒子附近不斷搜索，最終獲得食物的位置及距離食物最近的粒子。PSO算法尋優需要經過不斷進化，更新粒子的3個控制指標，并通過不斷比較，最終達到最 優解[8]。

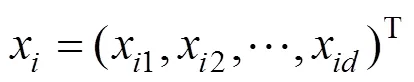
PSO算法經過不斷的進化，不斷的更新粒子的速度及位置，至第代的第維(=1,2,…,)的速度和位置可以采用如下表示：

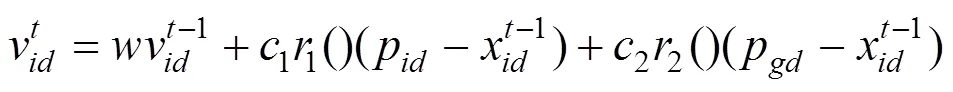
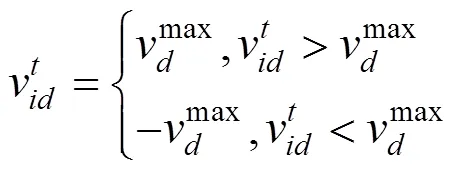
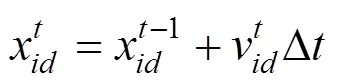
在進化迭代的過程中，個體不僅會記住自己信息還會借鑒群體中優秀粒子的信息。然而，隨著種群進化代數的增加，粒子的搜索空間不斷縮小，最終容易使PSO算法陷入局部最優，產生易早熟、后期迭代效率低的問題，借鑒遺傳算法中的變異思想，將變異操作代到PSO算法中，通過約束條件，對不合格的中間變量重新初始化，使粒子跳出局部極值，在更大的空間進行搜索，提高了PSO算法得到全局最優解的幾率。

本文采用引入變異功能的PSO算法搜索最優解的流程圖如圖2所示。

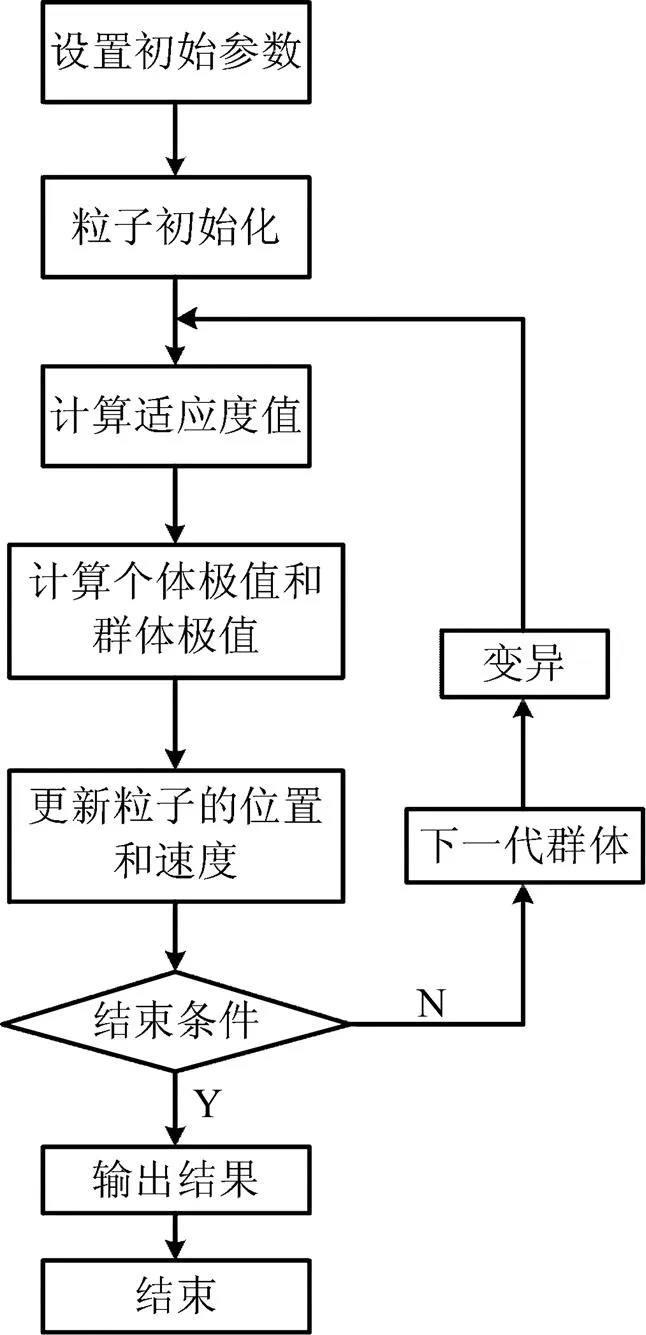
圖2 優化后的PSO算法尋優流程圖

1.3 基于SVM-PSO可靠度方法實現步驟

結合有限元模型計算及MATLAB計算平臺，提出的基于SVM-PSO方法結構可靠度分析過程如下。

1) 確定懸索橋運營狀態下隨機變量統計特征及概率分布，利用均勻設計法生成輸入樣本點。

2) 建立結構有限元模型，計算各輸入樣本對應的目標變量，得到輸出樣本，進而與輸入樣本構成訓練樣本。

3) 對樣本點進行數據歸一化處理，進行SVM參數尋優，得到SVM模型。

4) 隨機變量標準正態化，采用罰函數將約束優化問題轉化為無約束優化問題構造成適用于PSO算法求解的適應度方程，建立用于結構可靠指標求解的數學模型。

5) 使用優化后的PSO算法求得結構可靠指標。

1.4 算例驗證

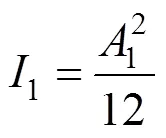
單位：m

表1 隨機變量統計參數

由表1，極限狀態方程含有3個隨機變量，采用均勻試驗設計在[?3,+3]內產生30個樣本，此時，該區間包含99.73%的點，滿足可靠度計算要求[9]。將輸入樣本代入極限狀態方程計算響應值(樣本輸出點)，將樣本輸入點與樣本輸出點共同組成訓練樣本，將樣本點歸一化后代入SVM中進行訓練，采用GA算法進行SVM參數優化，參數優化過程見圖4(a)，最小均方誤差MSE達到4.4×10?4，說明SVM能很好地逼近樣本點。由圖4(b)可知，本文建立的SVM模型能夠真實模擬結構極限狀態函數，具有良好的精度。

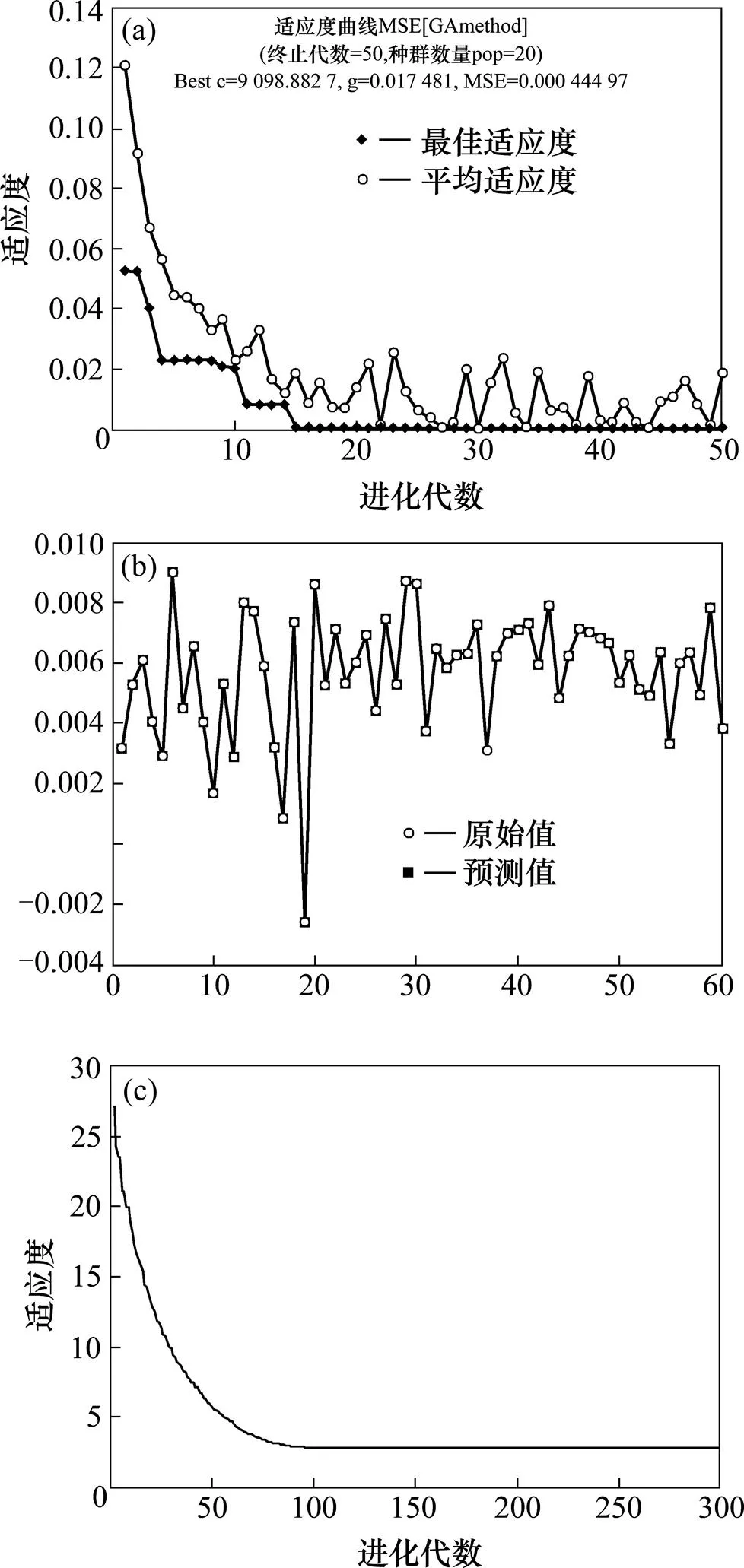
(a) GA參數優化；(b) SVM預測值與真實值對比；(c) PSO適應度值進化圖

采用罰函數方法將約束優化問題轉化成無約束優化問題求解，通過PSO算法進行進化迭代，迭代過程見圖4(c)，目標函數值達到收斂。

文獻[10]通過2 000次MC重要抽樣模擬得到本結構的失效概率為2.322 3×10?5，可靠度指標為2.830 7，文獻[11]通過63次抽樣，通過響應面分析法，得到本結構的失效概率為2.259 9×10?3，可靠度指標為2.839 4。采用基于SVM-PSO算法求解可靠指標，本例目標函數的可靠指標為2.843，與文獻結果相近，因此本文提出的SVM-PSO可靠度計算方法可行、準確。

2 基于撓度的懸索橋可靠度分析

2.1 工程概況

普立特大橋主跨采用628 m的雙塔單跨簡支鋼箱梁，橋梁全長1 040 m，跨徑形式為166+ 628+166m，矢跨比為1/10，橋面寬28.5 m，全橋共有102根吊索，左右幅分別為51根吊索。左右幅吊索橫橋向間距為26 m，主塔采用門式框架結構，由普立側主塔與宣威側主塔組成，主塔為鋼筋混凝土結構，采用C50混凝土澆筑而成，塔柱截面采用空心薄壁截面。鋼箱梁材料主要采用Q345D結構鋼，標準斷面高3 m，寬28.5 m。普立特大橋立面、標準斷面圖見圖5~6。

2.2 有限元模型

采用正版授權的MIDAS CIVIL進行有限元建模，采用空間梁單元模擬普立特大橋鋼箱梁和主塔，采用索單元模擬主纜和吊桿，采用桁架桿單元模擬散索鞍。利用懸索橋建模助手來建立普立特大橋，全橋模型如圖7所示。

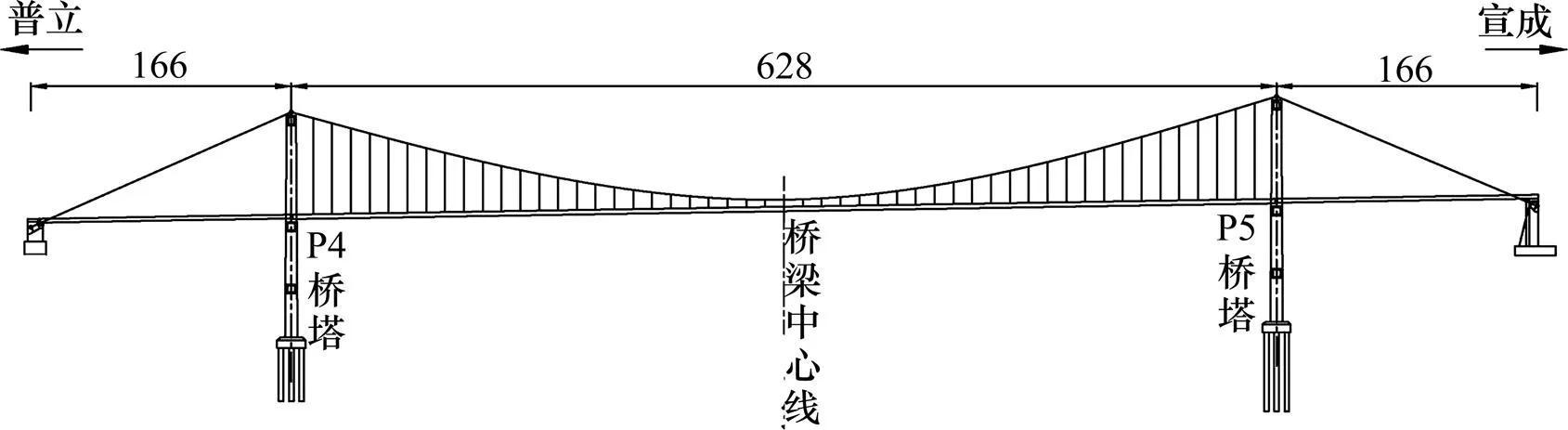
圖5 普立特大橋立面圖

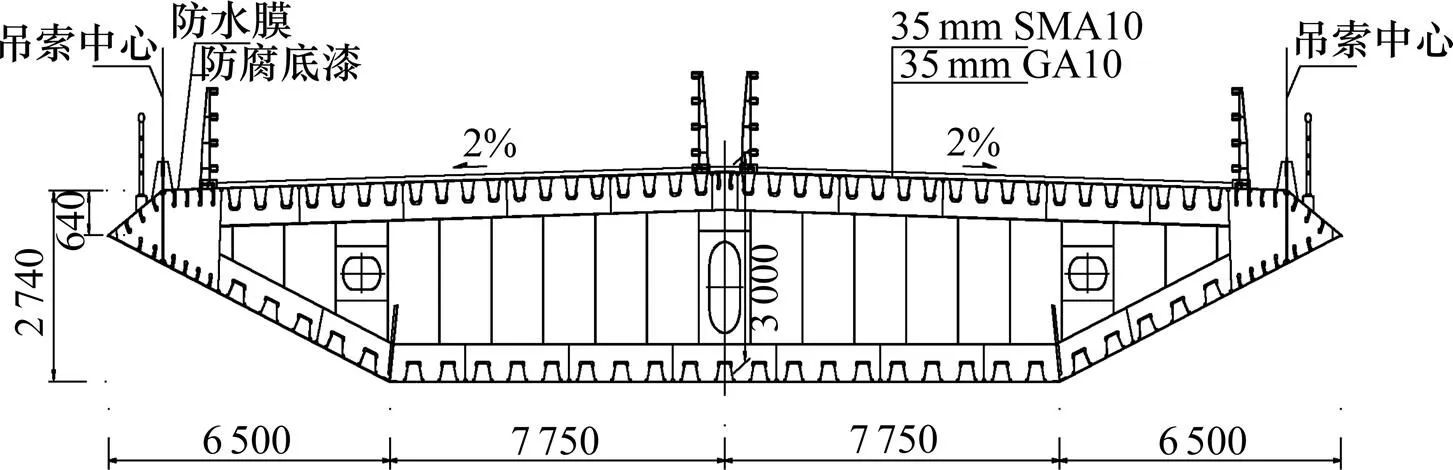
圖6 普立特大橋鋼箱梁標準斷面圖

圖7 全橋有限模型圖

2.3 懸索橋撓度功能函數

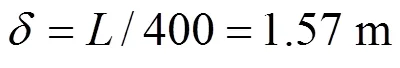
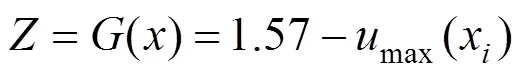
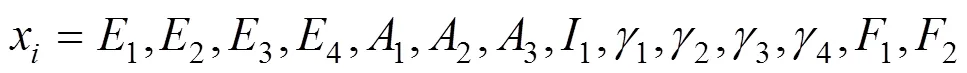
式中：1為鋼箱梁彈性模量；2為主纜彈性模量；3為吊索彈性模量；4為主塔彈性模量；1為鋼箱梁截面面積；2為主纜截面面積；3為吊索截面面積；1為鋼箱梁慣性矩；1為鋼箱梁容重；2為主塔容重；3為主纜容重；4為吊索容重；1為二期橫載；2為活荷載。

3 可靠度計算

3.1 隨機變量

由于材料性能、結構幾何尺寸以及外部荷載等的隨機性，實際結構所處的狀態與設計理論狀態有較大的差異，影響懸索橋運營階段線形的因素眾多，本文對結構質量安全進行控制，以幾何變形作為控制指標，主要從結構成橋狀態顯著性影響較大因素上，并參考文獻[5]和[13]，選取鋼箱梁彈模、容重、面積及鋼箱梁慣性矩，主塔彈模、容重及面積，主纜彈模、容重及面積，吊桿彈模、容重及面積，二期橫載及汽車荷載等隨機因素進行分析。各隨機變量的特征值參數見表2。

3.2 可靠指標計算

根據《工程結構可靠性設計統一標準》(GB 50153—2008)，并參考文獻[14]，可靠指標為4.0時，工程可靠度滿足要求，本文取4.0。以隨機參數變量1，2，3，4，1，2，3，1，1，2，3，4，1和2組成一個14維空間，采用均勻設計法在范圍[?3,+3]內產生100組隨機樣本，組成隨機輸入樣本，見表3(限于篇幅，本文僅列出前3項)。根據普立特大橋有限元分析模型，將上述樣本值分別依次代入有限元模型，各組隨機樣本對應的最大位移響應值，并根據式(8)得到訓練樣本的=()值，1=0.943，72=0.968 4，3=0.905 7…，組成訓練樣本，進行參數尋優，建立SVM模型。

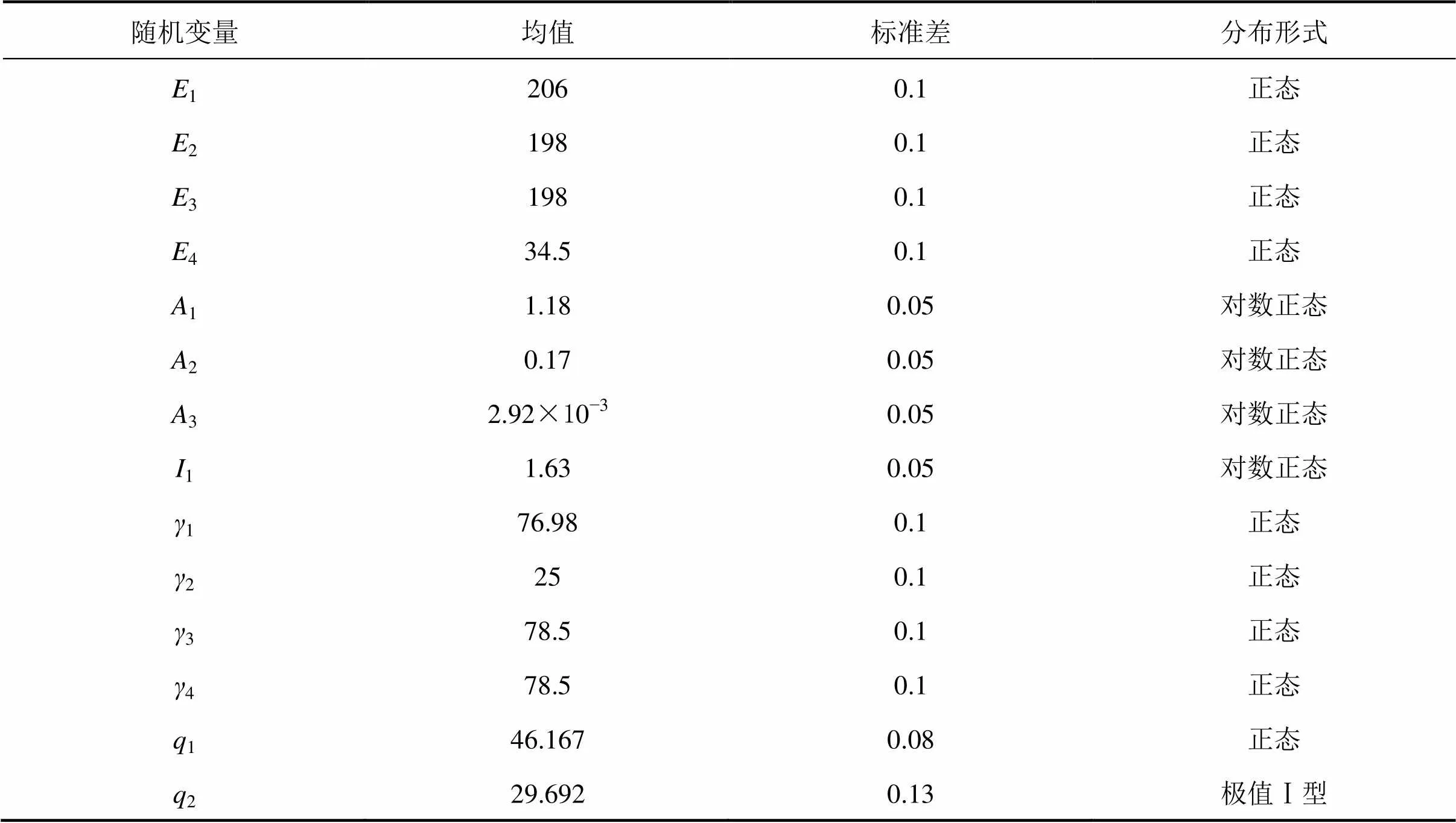
表2 隨機變量參數統計

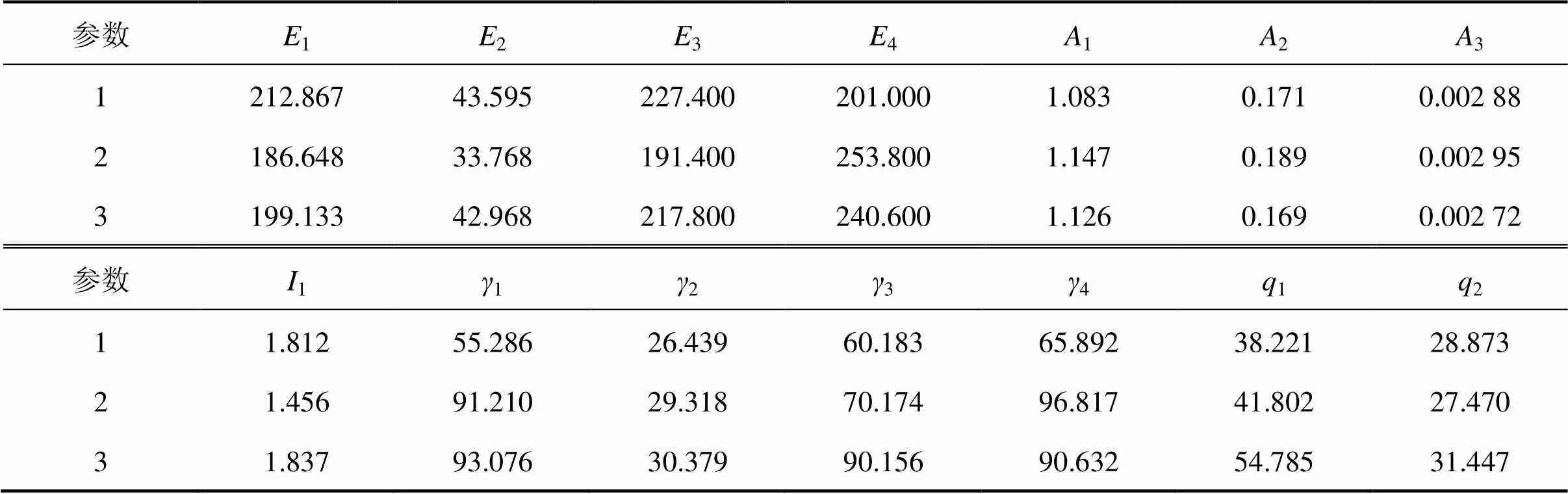
表3 均勻設計產生變量訓練樣本點

利用MATLAB計算平臺[15]，調用已建立的SVM模型，采用PSO優化算法進行可靠度計算，可靠指標=4.061，普立特大橋基于撓度控制可靠度滿足目標可靠指標要求。

4 結論

1) 借鑒遺傳算法思想，將變異操作代到PSO算法中，通過約束條件，對不合格的中間變量重新初始化，使粒子跳出局部極值，在更大的空間進行搜索，提高了PSO算法計算效率與精度。

2) 本文提出的SVM-PSO計算結構可靠度方法，運用有限元軟件與MATLAB數據處理軟件相結合，高效準確，可為同類型工程時變可靠度提供參考。

3) 采用本文提出的可靠度計算方法最終得到普立特大橋基于撓度的可靠指標為4.061，滿足正常使用極限條件下的要求，說明普立特大橋在汽車荷載作用下的位移具有較好的可靠性。

[1] 嚴小宇, 沈銳利, 唐茂林, 等. 基于可靠度理論的懸索橋主纜線形控制參數研究[J]. 建筑科學與工程學報, 2010, 27(3): 47?52.YAN Xiaoyu, SHEN Ruili, TANG Maolin, et al. Research on control parameter of main cable shape of suspension bridge based on reliability theory[J]. Journal of Architecture and Civil Engineering, 2010, 27(3): 47?52.

[2] 李廣奇, 程進. 基于神經網絡響應面法的大跨度懸索橋靜力可靠度分析[C]// 中國土木工程學會橋梁及結構工程分會. 第二十屆全國橋梁學術會議論文集(上冊).中國土木工程學會橋梁及結構工程分會, 2012: 8. LI Guangqi, CHENG Jin. Static reliability analysis of long span suspension bridges based on neural network response surface method[C]// The Twentieth China Bridge Conference Set (I), Bridge and Structural Engineering Branch China Civil Engineering Society, 2012: 8.

[3] 余曉琳. 自錨式懸索橋靜力可靠度研究[D]. 廣州: 華南理工大學, 2011. YU Xiaolin. Structural static reliability analysis of self-anchored suspension bridge[D]. Guangzhou: South China University of Technology, 2011.

[4] AN Xuwen, Gosling P D, ZHOU Xiaoyi. Analytical structural reliability analysis of a suspended cable[J]. Structural Safety, 2016, 58: 20?30.

[5] 李建慧,李愛群. 自錨式懸索橋靜力隨機分析與可靠度評估[J]. 中國公路學報, 2012, 25(6): 74?79. LI Jianhui, LI Aiqun. Stochastic analysis of static characteristics and reliability assessment for self-anchored suspension bridge[J]. China Journal of Highway and Transport, 2012, 25(6): 74?79.

[6] Hurtado Jorge E. Filtered importance sampling with support vector margin: A powerful method for structural reliability analysis[J]. Structural Safety, 2007, 29: 2?15.

[7] 史峰, 王小川, 郁磊, 等. MATLAB神經網絡30個案例分析[M]. 北京: 北京航空航天大學出版社, 2014. SHI Feng, WANG Xiaochuan, YU Lei, et al. 30 cases analysis of MATLAB neural network[M]. Beijing: Beihang University Press, 2014.

[8] 楊維, 李歧強. 粒子群優化算法綜述[J]. 中國工程科學, 2004, 6(5): 87?94. YANG Wei, LI Qiqiang. Survey on particle swarm optimization algorithm[J]. Engineering Science, 2004, 6(5): 87?94.

[9] 張紅顯. 基于支持向量機的PC剛構橋施工期可靠度研究[D]. 西安: 長安大學, 2017. ZHANG Hongxian. Reliability analysis of PC rigid frame bridge during construction based on SVM[D]. Xi’an: Chang’an University, 2017.

[10] DENG J, GU D, LI X, et al. Structural reliability analysis for implicit performance functions using artificial neural net work[J]. Structural Safety, 2005, 35(3): 459?467.

[11] 李生勇. 自錨式懸索橋結構可靠性研究[D]. 大連: 大連理工大學, 2007. LI Shengyong. The research on the structural reliability for self-anchored suspension bridges[D]. Dalian: Dalian University of Technology, 2007.

[12] JTG-T D65?05?2015, 公路懸索橋設計規范[S]. JTG-T D65?05?2015, Specifications for design of highway suspension bridge[S].

[13] 張運濤, 孟少平, 張速. 基于響應面法的橋梁結構徐變效應分析[J]. 中國公路學報, 2011, 24(1): 78?82. ZHANG Yuntao, MENG Shaoping, ZHANG Su. Creep effect analysis of bridge structure based on response surface methodology[J]. China Journal of Highway and Transport, 2011, 24(1): 78?82.

[14] 楊小剛, 秦權. 公路混凝土橋涵設計規范設計表達式可靠指標的誤差及改進[J]. 工程力學, 2008, 25(11): 116?121. YANG Xiaogang, QIN Quan. Errors and improvements in reliability indexes of design formulate of current China codes for design of highway RC bridges[J]. Engineering Mechanics, 2008, 25(11): 116?121.

[15] 張明. 結構可靠度分析:方法與程序[M]. 北京: 科學出版社, 2009. ZHANG Ming. Structural reliability analysis: methods and procedures[M]. Beijing: Science Press, 2009.

Research on reliability of deflection control for long-span suspension bridge based on SVM-PSO

DENG Haibo1, CHANG Zhugang1, LI Hutao2, ZHANG Hongxian1

(1. Changsha Planning & Design Institute Co., Ltd, Changsha 410007, China; 2. T. Y. Lin International Engineering Consulting (China) Co., Ltd, Chongqing 404100, China)

In order to study the reliability of deflection for long-span suspension bridge at operation stage with high dimensional random parameters, this paper established bridge deflection reliability model based on SVM (support vector machine) as well as using finite element method. Combined with the PSO (particle swarm optimization), the reliability index of deflection in structural operation stage was calculated. The result shows that by using the idea of mutation in the genetic algorithm, the problem of premature convergence and low efficiency of the particle swarm optimization can be solved by setting the constraints of intermediate variables, thus improving the efficiency and accuracy of the algorithm.Structural reliability method based on SVM-PSO algorithm is efficient and accurate, and the deflection reliability of the bridge meets the requirements under the normal use limit condition.

support vector machine; particle swarm optimization; reliability;deflection; finite element method

10.19713/j.cnki.43?1423/u.2019.01.016

U445.4

A

1672 ? 7029(2019)01 ? 0114 ? 07

2017?12?28

國家自然科學基金資助項目(51678072，51478472)

常柱剛(1980?)，男，湖南長沙人，高級工程師，從事橋梁結構理論及橋梁設計優化研究；E?mail：405587061@qq.com

(編輯 陽麗霞)