擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸運動誤差測量與辨識

郭世杰 姜歌東 梅雪松

(1.內(nèi)蒙古工業(yè)大學機械工程學院， 呼和浩特 010051; 2.西安交通大學機械工程學院， 西安 710049)

0 引言

與三軸機床相比，五軸機床有兩個旋轉(zhuǎn)軸，因此它可以同時調(diào)節(jié)刀具相對工件的位姿[1]，由此可提高加工效率并提升加工表面質(zhì)量[2]。然而，兩個旋轉(zhuǎn)軸也為機床引入了更多的誤差源，其中幾何誤差占機床總誤差的40%～50%[3-4]。幾何誤差是決定機床準靜態(tài)精度的重要因素，幾何誤差是幾何精度的直接體現(xiàn)，通過實施誤差補償技術可有效保證和提升機床幾何精度[5]。誤差補償技術由幾何誤差建模、誤差測量及辨識、誤差補償3部分組成[6]。幾何誤差測量及辨識是利用幾何誤差模型實施誤差預測的關鍵，也是進行誤差補償?shù)那疤幔虼酸槍ξ遢S機床旋轉(zhuǎn)軸幾何誤差測量及辨識，國內(nèi)外眾多學者展開了較多的研究[7-10]。幾何誤差分為運動誤差(位置相關幾何誤差)和位姿誤差(位置無關幾何誤差)兩類[11-12]，前者主要源于制造過程，后者主要形成于裝配過程。基于多軸同步運動驅(qū)動球桿儀(DBB)可實現(xiàn)圓軌跡測量，利用幾何誤差與圓測量軌跡之間的映射關系，可辨識搖籃式五軸機床旋轉(zhuǎn)軸的位姿誤差[13-14]。將DBB安裝于旋轉(zhuǎn)軸誤差敏感方向上，通過旋轉(zhuǎn)軸單軸運動，可實現(xiàn)旋轉(zhuǎn)軸運動誤差辨識[15-18]。在此基礎上，設計一次安裝狀態(tài)下的空間軌跡測量，可有效避免安裝誤差對測量結(jié)果的影響[19]。與需進行多組測量軌跡的測量方法相比[20-21]，基于激光跟蹤儀[22]及R-test[23]的誤差測量方法測量路徑較為簡單，但需要建立較為復雜的辨識模型。

上述研究對降低旋轉(zhuǎn)軸幾何誤差的影響起到了重要推動作用，然而機床結(jié)構(gòu)的差異性致使現(xiàn)存測量方法通用性弱。DBB與激光干涉儀、跟蹤儀及R-test儀相比成本低，易于實現(xiàn)工業(yè)現(xiàn)場的機床幾何精度檢測[17]，而現(xiàn)有的利用DBB進行旋轉(zhuǎn)軸幾何誤差的研究主要應用于搖籃式五軸機床，針對擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸的運動誤差測量及辨識的方法較少[20,24]，已有的利用DBB對擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸運動誤差的測量、辨識方法中，裝夾次數(shù)較多、易受安裝誤差累積效應的影響。

鑒于此，本文以擺頭轉(zhuǎn)臺型五軸機床為研究對象，在已有研究基礎上提出一種基于DBB的五次安裝測量、辨識方法。首先，依據(jù)擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸空間結(jié)構(gòu)特點，對旋轉(zhuǎn)軸運動誤差在其局部坐標系下進行表征并建立運動誤差測量模型。其次，利用DBB測量過程對誤差敏感方向的特征，建立DBB的安裝模式并將DBB相同的初始安裝位置的測量模式合并，構(gòu)造基于DBB測量的五次安裝法，基于DBB測量值辨識擺頭轉(zhuǎn)臺型五軸機床2個旋轉(zhuǎn)軸的12項運動誤差，通過減少安裝次數(shù)提升測量及辨識的準確性和精準度。最后，根據(jù)所提出的五次安裝法旋轉(zhuǎn)軸運動誤差檢測方案，運用DBB在擺頭轉(zhuǎn)臺型五軸機床上進行實驗，利用辨識結(jié)果進行誤差補償前后的精度對比，以驗證該方法的有效性與可行性。

1 五軸機床旋轉(zhuǎn)軸運動誤差建模

1.1 旋轉(zhuǎn)軸的運動誤差

擺頭轉(zhuǎn)臺型五軸機床結(jié)構(gòu)如圖1a所示。擺頭轉(zhuǎn)臺型五軸機床結(jié)構(gòu)由X軸、Y軸和Z軸3個直線軸，以及C軸和B軸兩個旋轉(zhuǎn)軸組成。旋轉(zhuǎn)軸幾何誤差中的運動誤差與運動軸的指令位置相關，即運動誤差隨著指令位置發(fā)生改變。因此C旋轉(zhuǎn)軸及B旋轉(zhuǎn)軸的運動誤差可表達為旋轉(zhuǎn)角c及b的函數(shù)。旋轉(zhuǎn)軸的6項運動誤差如圖1b所示。其中，δi(j)表示位置誤差，εi(j)表示角度誤差，相應的j表示位置坐標，i表示誤差所在方向。

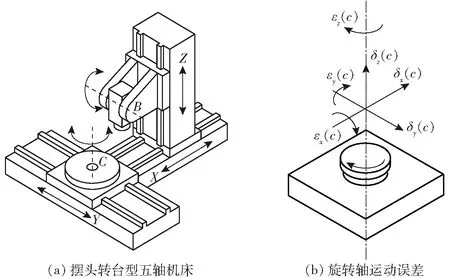
圖1 機床結(jié)構(gòu)及運動誤差示意圖Fig.1 Schematics of machine tool and motion errors

圖1a中的擺頭轉(zhuǎn)臺型五軸機床的B旋轉(zhuǎn)軸具有6項運動誤差，分別是X、Y、Z方向的位置誤差δx(b)、δy(b)、δz(b)和繞X、Y、Z軸角度誤差εx(b)、εy(b)、εz(b)。對C軸而言，6項運動誤差分別是3項位置誤差：δx(c)、δy(c)、δz(c)和3項角度誤差：εx(c)、εy(c)、εz(c)。

1.2 擺頭轉(zhuǎn)臺型五軸機床測量坐標系的建立

由于運動誤差表征運動軸在理想軸線位置方向上的運動偏差，因此依據(jù)多體系統(tǒng)理論進行誤差建模時，將旋轉(zhuǎn)軸所包含的運動誤差在所對應的運動軸的局部坐標系下進行定義和描述，這與運動誤差的本質(zhì)特征相符，也與運動誤差表達時矩陣相乘的運算規(guī)則相對特征體局部坐標系進行定義的形式一致。

定義機床坐標系位于工作臺中心，B軸坐標系XbYbZb與主軸坐標系XsYsZs重合。Y軸坐標系XyYyZy、X軸坐標系XxYxZx、Z軸坐標系XzYzZz建立于各組成軸上，以上局部坐標系方向與參考系XRYRZR一致。C軸和B軸的測量坐標系XcYcZc、XbYbZb與各局部坐標系之間位置關系如圖2所示。對擺頭轉(zhuǎn)臺型五軸機床而言，通過將旋轉(zhuǎn)軸的運動誤差固結(jié)于所建立的局部坐標系下進行描述，可實現(xiàn)在各旋轉(zhuǎn)軸局部坐標系下的軌跡測量，易于誤差建模和辨識的進行。

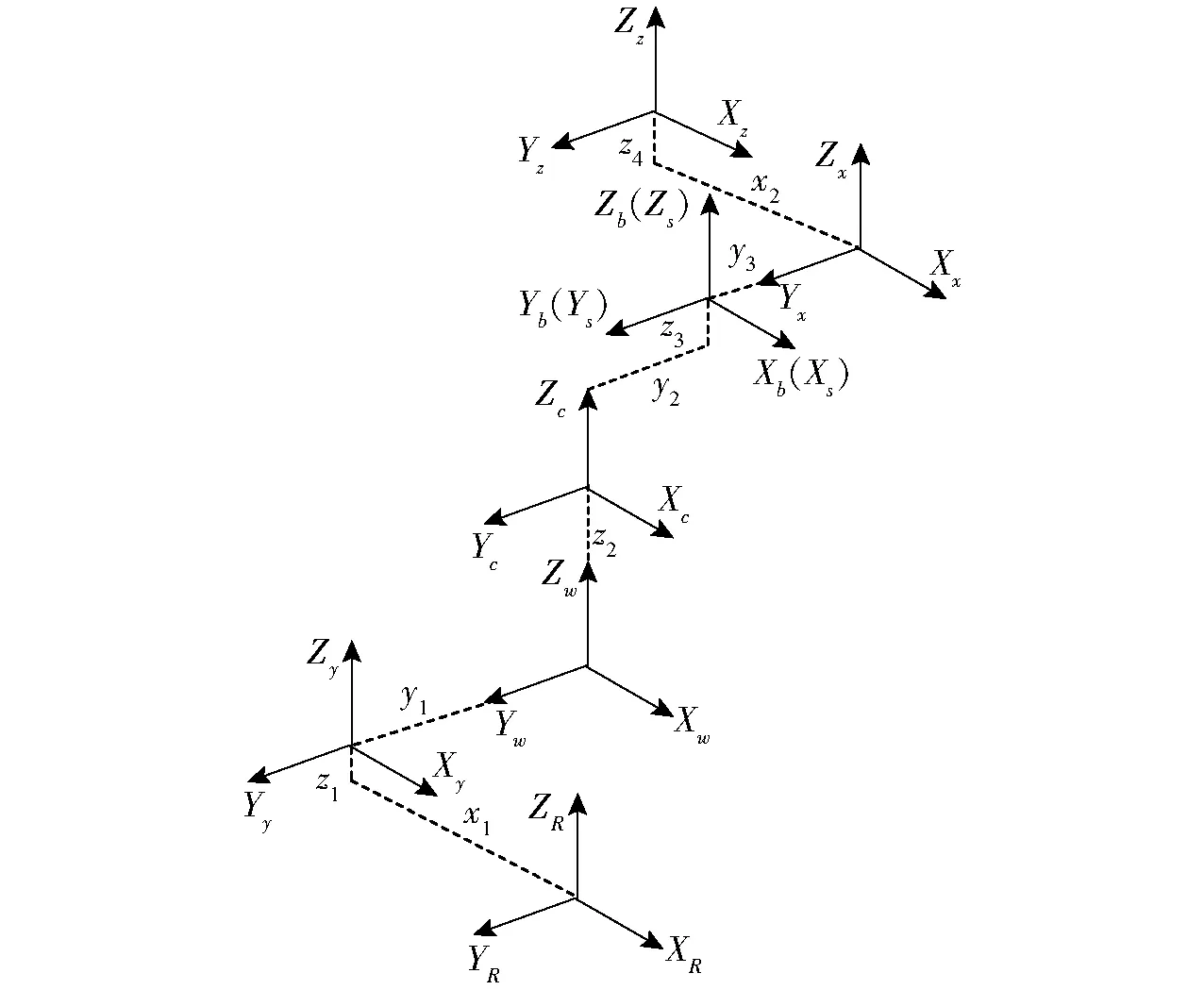
圖2 旋轉(zhuǎn)軸局部坐標系示意圖Fig.2 Structure schematic of local coordinate systems

1.3 擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸運動誤差測量模型

DBB是檢測機床精度的有效工具，在具有圓弧插補功能的數(shù)控機床上，可通過多軸聯(lián)動或主軸端旋轉(zhuǎn)軸轉(zhuǎn)動帶動主軸端DBB支座運動，驅(qū)動工作臺帶動安裝其上的DBB支座運動，圓運動過程中可伸縮桿檢測兩接觸球球心間距離相對圓運動半徑的誤差，并形成圓運動的誤差軌跡，結(jié)合幾何誤差模型可實現(xiàn)誤差解耦及誤差項的最終辨識[1,13]。由五軸機床空間幾何誤差的齊次表達形式可知，五軸機床的特征體i和相鄰低序體單元j之間的位置關系可由齊次變換矩陣表示為

(1)

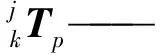
球桿儀的接觸球O2和O1在測量坐標系中的位置為Po2=(x2，y2，z2)T，Po1=(x1，y1，z1)T。不考慮運動誤差對旋轉(zhuǎn)軸精度的影響時，小球Oj的理想變換矩陣為

(2)

當旋轉(zhuǎn)軸C運動而轉(zhuǎn)動軸B保持靜止時，與角b相關的矩陣是單位陣；類似的，當旋轉(zhuǎn)軸B運動而旋轉(zhuǎn)軸C保持靜止時，與角c相關的矩陣是單位陣。考慮旋轉(zhuǎn)軸的運動幾何誤差影響機床精度，小球Oj在實際狀態(tài)下的變換關系表達為

(3)

利用旋轉(zhuǎn)軸驅(qū)動球桿儀實現(xiàn)圓軌跡測量時，DBB的接觸Oj的理想位置和實際位置為

(4)

(5)

將式(3)代入式(4)，式(2)代入式(5)，可確定理想狀態(tài)下DBB接觸球之間的距離iL和實際狀態(tài)下接觸球間距離aL，其表達形式為

iL=iPo2-iPo1

(6)

aL=aPo2-aPo1

(7)

DBB接觸球之間的長度變化值在3個方向是空間誤差向量，可以表示為

[ΔxΔyΔz1]=aL-iL

(8)

將式(6)、(7)和齊次變換矩陣代入式(8)可確定誤差向量的具體表達式。對C軸運動幾何誤差進行測量時，需保證主軸端接觸球不受B旋轉(zhuǎn)軸運動的影響，以此實施圓軌跡測量可以得到C軸的空間誤差向量，結(jié)果為

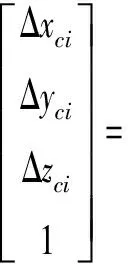
(9)

式中，下標i表示測量模式，下標j表示安裝位置。

類似的，對旋轉(zhuǎn)軸B的運動幾何誤差進行辨識時，將相關的誤差矩陣代入式(8)后，可得B軸誤差向量表達式為

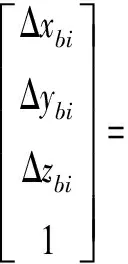
(10)

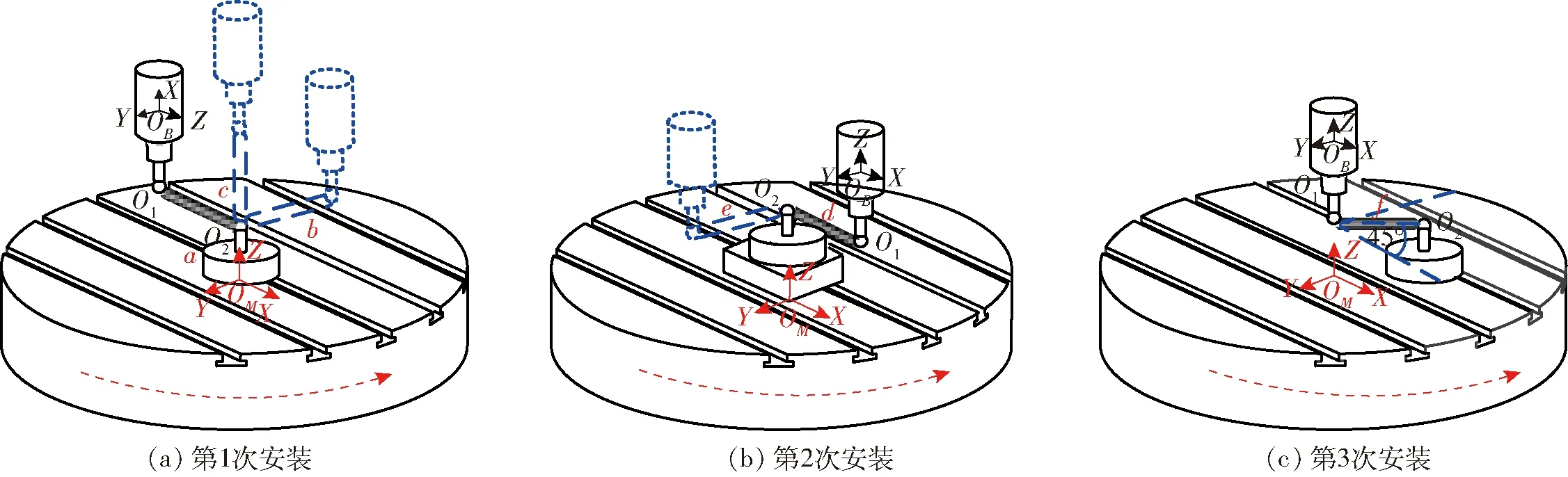
圖3 辨識C軸運動幾何誤差的安裝測量模式Fig.3 Installation and measurement modes for identifying motion errors of C axis

2 基于五次安裝法的運動幾何誤差測量及辨識

基于五次安裝法的PDGEs測量及辨識的基本思路是：通過設置DBB的接觸球在測量坐標下的初始位置，保證旋轉(zhuǎn)軸相同初始安裝位置下的圓軌跡測量相繼進行，然后改變DBB的安裝位置實施下一安裝位置下的軌跡測量。利用旋轉(zhuǎn)軸單獨運動以及直線軸聯(lián)動可直接實現(xiàn)一次安裝不同測量模式之間的切換，在此過程中DBB的磁致伸縮桿不與兩個球面支承座分離，其本質(zhì)屬于同一次安裝[19,21]。

2.1 C軸的測量模式及辨識

當測量坐標系與旋轉(zhuǎn)軸的軸心位置重合，且DBB的球桿與測量坐標系的軸線平行時，DBB磁致伸縮桿對相應方向的誤差最為敏感[11-12,16]。因此可通過設置球桿儀安裝位置和方向，實現(xiàn)DBB的可伸縮桿沿旋轉(zhuǎn)軸坐標系的坐標軸方向相對靜止，通過上述處理可有效提升測量及辨識效率。此外，為簡化辨識過程、提升辨識結(jié)果的準確性，需要限制旋轉(zhuǎn)軸B軸與旋轉(zhuǎn)軸C軸同步運動形式的出現(xiàn)，由此可實現(xiàn)B軸的運動幾何誤差不影響C軸的辨識結(jié)果，即通過設置旋轉(zhuǎn)軸的運動形式保證辨識過程中兩個旋轉(zhuǎn)軸的運動幾何誤差測量過程中的線性無關。

通過上述方式可確保主軸端接觸球沿刀具鏈在機床C軸定義的測量坐標系下位置不發(fā)生變化，因此只需考慮安裝于轉(zhuǎn)臺端C軸坐標下的接觸球受C軸運動幾何誤差的影響。由式(9)和式(10)可知，幾何誤差在3個方向上的誤差分量、球桿儀工作臺端接觸球位置以及幾何誤差項之間可表達為矩陣形式，利用最小二乘法可準確辨識6項誤差，也可通過設計不同測量位置，利用測量坐標系內(nèi)不同位置的圓軌跡測量數(shù)據(jù)確定6項幾何誤差解析解。

由運動誤差的矩陣表達形式可知，運動誤差與機床的綜合幾何誤差模型無關，僅與測量模型相關。因此需考慮測量坐標系下誤差項與DBB安裝位置之間的關系，選擇合適的坐標位置使上述包含位置坐標的矩陣形式為非奇異矩陣，由此構(gòu)造出6個線性無關的正定方程。式(9)、(10)中(xi，yi，zi)(i=1,2,…,6)是工作臺一側(cè)接觸球在C軸坐標(測量坐標)系下的初始安裝位置。測量過程中，DBB對使其伸縮桿產(chǎn)生位移變形方向的誤差最為明顯，因此，可據(jù)此設計球桿儀的放置方向。對C旋轉(zhuǎn)軸所設計的DBB安裝位置如圖3所示。

設置上述3次安裝并建立a～f測量模式，此時對C軸的測量需要3次安裝。具體步驟如下：

如圖3所示，在對DBB實施第1次安裝并進行模式a下的圓軌跡測量時，工作臺端小球O2安裝于轉(zhuǎn)臺中心，球桿儀的伸縮桿平行于X軸，主軸端接觸球O1與接觸球O2距離為DBB的公稱長度L。測量過程中，僅有旋轉(zhuǎn)軸C軸運動其他運動軸均保持靜止。此時在C軸的驅(qū)動下僅有工作臺端小球運動，主軸端接觸球O1靜止。這樣球桿儀僅對旋轉(zhuǎn)軸C軸X方向的誤差敏感，即僅有C軸沿X方向的誤差對測量有影響。在此時測量模式下，球桿儀測量值ΔR與幾何誤差的關系為

ΔRCa=Δxca=δx(c)

(11)

類似的，在b、c測量模式下進行沿Y軸和Z軸方向的安裝時，可實現(xiàn)對C軸沿Y方向和沿C軸Z方向的誤差測量。此時，在b、c測量模式下，球桿儀測量值ΔR與幾何誤差的關系為

ΔRCb=Δycb=δy(c)

(12)

ΔRCc=Δzc=δz(c)

(13)

圖4 辨識B軸運動誤差的安裝測量模式Fig.4 Installation and measurement modes for identifying motion errors of B axis

在對DBB實施第2次安裝并進行模式d下的圓軌跡測量時，首先在Z方向上提升工作臺端接觸球O2與轉(zhuǎn)臺中心的距離后，改變B軸與接觸球O1的距離后對球桿儀進行安裝。與第1次安裝下的測量模式a類似，球桿儀的伸縮桿平行于X軸，主軸端小球O1與O2距離為DBB的公稱長度L。測量過程中，僅有旋轉(zhuǎn)軸C軸運動，其他運動軸均保持靜止。由于工作臺端小球安裝位置的改變，在Z方向測量坐標系與小球O2的球心位置不重合，除了C軸沿X方向的誤差對測量有影響外，C軸沿Z方向的誤差也會對測量有影響。由于在測量模式a中已經(jīng)辨識了C軸沿X方向的誤差δx(c)，此時C軸沿Z方向的運動誤差可辨識，二者與球桿儀讀數(shù)之間的關系可表達為

ΔRCd=z4εy(c)+δx(c)

(14)

類似的，在e測量模式下進行沿Y的安裝時，可實現(xiàn)C軸沿Y方向的誤差測量。此時，球桿儀讀數(shù)的相對表達形式ΔR可表達為

ΔRCe=-z5εx(c)+δy(c)

(15)

在對DBB實施第3次安裝并進行模式f下的圓軌跡測量時，球桿儀的安裝如圖3c所示。此時主軸端小球位于轉(zhuǎn)臺中心上方，DBB的可伸縮桿平行于XOY平面，且工作臺端接觸球O2的初始位置在X軸與Y軸的角平分線。測量過程中，僅有旋轉(zhuǎn)軸C軸運動，其他運動軸均保持靜止。由于工作臺端接觸球O2的改變，在XOY平面內(nèi)C軸沿X方向的誤差和C軸沿Z方向的誤差均對測量有影響，此時影響測量軌跡的誤差與球桿儀讀數(shù)之間的關系可表達為

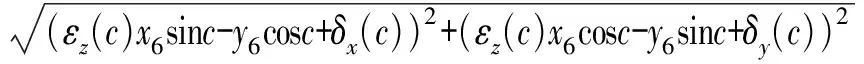
(16)

由式(11)～(16)可知，確定工作臺端小球O2的初始安裝位置后，δx(c)、δy(c)、δz(c)、εx(c)、εy(c)可由式(12)～(15)確定辨識值，將測量模式a和測量模式b辨識出的幾何誤差δx(c)、δy(c)的解析解代入式(16)后可辨識出滾轉(zhuǎn)誤差εz(c)，由此可辨識C旋轉(zhuǎn)軸的6項運動幾何誤差。

2.2 B軸測量模式及辨識

由于B軸的坐標系與工作臺之間的空間距離較大，無法將球桿儀的磁性底座準確安裝于B軸的軸線上，因此對B軸的測量辨識與C軸的測量及安裝模式不同。當B軸轉(zhuǎn)動帶動主軸端小球運動時，需要通過直線軸與旋轉(zhuǎn)軸的聯(lián)動方式實現(xiàn)圓/圓弧運動軌跡的測量。

對B軸測量時以B軸的局部坐標系為測量基準坐標系。圖4是設計的DBB安裝示意簡圖。在對DBB第1次安裝后進行B軸a模式下的測量，主軸端接觸球O1安裝于距離B軸沿X方向Lb處，工作臺端接觸球O2在B軸坐標系下的位置是(R+Lb, 0,H1)。DBB第1次安裝后的B軸a測量模式下，進行圓軌跡測量過程中B軸順時針轉(zhuǎn)動，Z軸與X軸通過直線插補形成圓弧軌跡，C軸和Y軸保持靜止。

DBB對B軸沿X方向的幾何誤差敏感，此時接觸球O2與O1之間的距離在X軸方向的投影表征了球桿儀長度。幾何誤差影響下的球桿儀長度變化與誤差項之間的關系為

ΔRBa=Lbεy(b)sinb+δx(b)+H1εy(b)cosb

(17)

在對DBB第1次安裝后測量模式b下，此時球桿儀對B軸沿Y軸方向的誤差敏感。通過B軸的順時針轉(zhuǎn)動，Z軸與X軸通過直線插補形成圓弧軌跡，C軸和Y軸保持靜止。幾何誤差影響下的球桿儀長度變化值與誤差項之間的關系為

ΔRBb=δy(b)+H1(εz(b)sinb-εx(b)cosb)

(18)

在對DBB第2次安裝后c測量模式下，幾何誤差影響下的球桿儀長度變化值與誤差項之間的關系為

ΔRBc=H1εy(b)cosb+δx(b)

(19)

在對DBB第2次安裝后的d測量模式下，主軸端接觸球O1在B軸坐標系下的位置是(R,0,H1)，工作臺端接觸球O2安裝于X軸方向上，在B軸坐標系下的位置是(R,0,H1-R)，此時DBB的可伸縮桿平行于Z軸。幾何誤差影響下的球桿儀長度變化與誤差項之間的關系為

ΔRBd=-H1εy(b)sinb+δz(b)

(20)

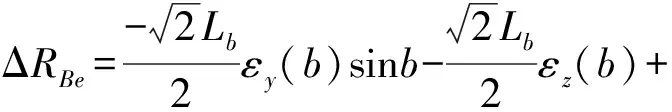
(21)

在對DBB第4次安裝后的測量模式f中，主軸端接觸球O1安裝于B軸坐標下的(0,0,H2)處，工作臺端接觸球O2安裝于坐標系下(0,R,H2)處。DBB的可伸縮桿平行于Y軸方向。此時，幾何誤差影響下的球桿儀長度變化與誤差項之間的關系為

ΔRBf=H2[εz(b)sinb-εx(b)cosb]+δy(b)

(22)

通過測量模式a的辨識表達式(17)和測量模式c的辨識表達式(19)可知角度誤差εy(b)的辨識表達式為

(23)

將式(23)代入式(20)，可得δz(b)的表達式為

(24)

將式(23)代入式(19)，可得δx(b)的表達式為

(25)

求解式(21)，可得到角度誤差εz(b)的辨識表達式為

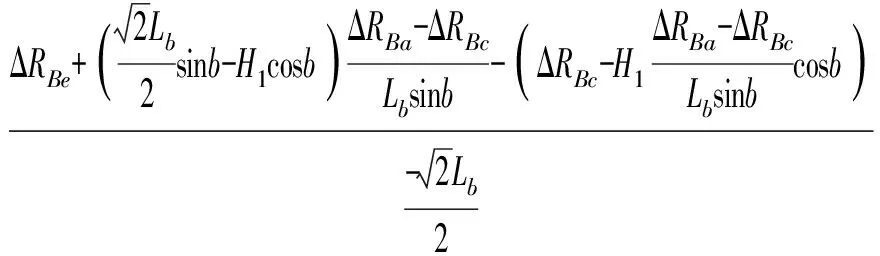
(26)

基于已經(jīng)辨識的εz(b)，由式(18)和式(22)可辨識出εx(b)，其表達式為

(27)

利用εz(b)的辨識值，可以確定δy(b)的辨識表達式為

(28)

2.3 五次安裝法的建立

B軸坐標系中心位置距離工作臺表面沿Z向距離較大，這導致構(gòu)造B軸的運動幾何誤差辨識方程時DBB的安裝位置較C軸多。但依據(jù)在相同的初始安裝位置可連續(xù)實施不同平面內(nèi)的測量，且球桿儀僅需安裝一次的特點，本文將相同的初始安裝位置的測量模式合并構(gòu)造基于DBB測量的五次安裝法。

由C軸和B軸所述的DBB安裝及測量特征可知：旋轉(zhuǎn)軸C軸的測量模式d、e與測量B軸的測量模式f相比，主軸端接觸球和工作臺端接觸球在機床坐標系下的初始位置存在相似之處。此時可利用旋轉(zhuǎn)軸單獨運動以及直線軸聯(lián)動直接實現(xiàn)一次安裝不同測量模式之間的切換。類似的情況在C軸測量模式f與B軸測量模式c、d之間也存在。因此，本研究所提出的測量方法可依據(jù)上述特點進行安裝次數(shù)的簡化，基于DBB測量流程如圖5所示。

圖5 基于DBB測量的五次安裝法測量流程Fig.5 Measuring process of five installation method based on DBB

圖6 五次安裝法實驗現(xiàn)場Fig.6 Experimental setup of five installation method

五次安裝法與其他方法[19-20]相比可有效減少DBB的安裝次數(shù)，這樣可以節(jié)省安裝時間，同時可進一步避免安裝誤差對測量結(jié)果一致性的影響。

3 實驗驗證

為驗證所提出的五次安裝測量方法的準確性，在如圖6所示的五軸加工中心上進行實驗研究。在進行旋轉(zhuǎn)軸的運動幾何誤差測量前，先進行直線軸的幾何誤差測量及補償[1,11]，環(huán)境溫度控制在(20±2)℃內(nèi)，由此最大程度降低熱誤差對測量結(jié)果的影響。

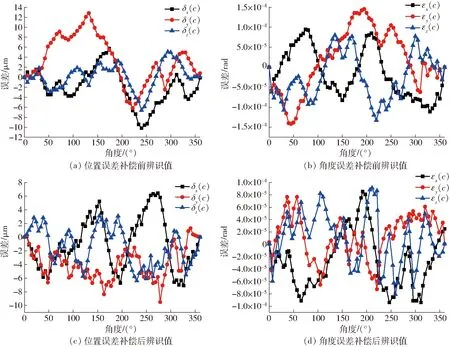
圖7 C軸運動誤差辨識結(jié)果對比Fig.7 Comparison of motion errors of C axis

依據(jù)五次安裝法建立的測量模式，利用桿儀進行圓軌跡測量。整個測量過程包括DBB的五次安裝，其中安裝參數(shù)Lb=100 mm，R=100 mm，H1=384.67 mm，H2=484.67 mm。C軸安裝模式下，B軸靜止不動，C軸的進給率500 mm/min，C軸的越程角為180°，順時針和逆時針的運動行程是360°。B軸運動模式下，B軸的進給率是500 mm/min，B軸的越程角為5°，順時針和逆時針的運動行程是90°。同一測量模式進行多組數(shù)據(jù)測量，并保存數(shù)據(jù)。依據(jù)五次安裝法測量流程執(zhí)行完上述的圓軌跡測量后，利用所建立的辨識模型可解耦得到C軸和B軸的12項運動幾何誤差，辨識結(jié)果如圖7、8所示，利用辨識值通過逆運算確定補償值的解析解[8,13]。

由圖7可知，誤差補償后C軸的位置誤差最大值由12.83 μm降低至9.53 μm，角度誤差最大值由1.45×10-4rad降低至7.0×10-5rad。C軸的最低補償率是15.85%，平均補償率是48.89%，最大補償率達到了92.42%。

圖8 B軸運動誤差辨識結(jié)果對比Fig.8 Comparison of motion errors of B axis

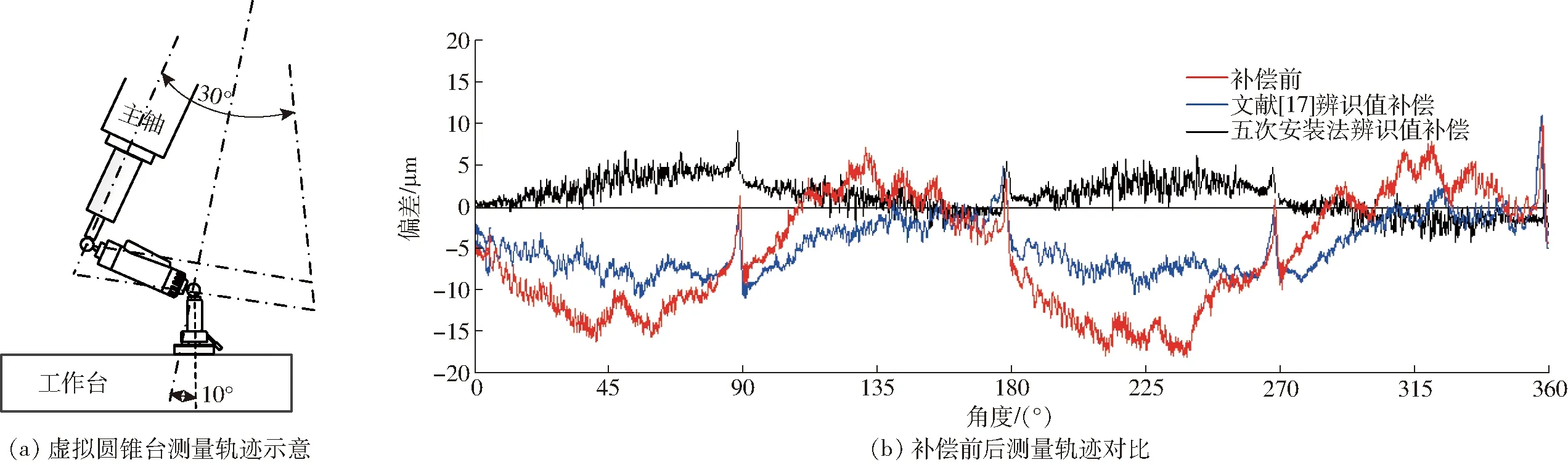
圖9 圓錐臺測量軌跡及測量結(jié)果Fig.9 Measurement track and measurement results of frustum of cone

由圖8c和圖8d可知，誤差補償后B軸的位置誤差最大值由9.65 μm降低至7.11 μm，角度誤差最大值由1.6×10-4rad降低至2.0×10-5rad。B軸的最低補償率是26.45%，平均補償率是51.49%，最大補償率達到了87.26%。為進一步驗證辨識值的準確性，依據(jù)ISO 230-1標準利用五軸同步運動驅(qū)動DBB進行虛擬圓錐臺軌跡測量[12,25]，并分別進行誤差補償前空間圓錐臺軌跡測試(測量軌跡如圖9a)，以及依據(jù)文獻[17]的測量方法(六次安裝)和本文的五次安裝法確定辨識值，并進行誤差補償后空間錐臺軌跡測量，結(jié)果如圖9b所示。

由圖9b可知，運動誤差補償前圓軌跡的半徑偏差平均值達9.5 μm，依據(jù)文獻[17]所提出的測量辨識方法確定幾何誤差數(shù)值實施誤差補償后，圓軌跡的半徑偏差平均值為6.8 μm，利用五次安裝法進行誤差辨識及補償后，圓軌跡的半徑偏差平均值為4.7 μm，降低了50.52%。采用文獻[17]的測量辨識方法進行補償后，半徑偏差明顯降低，依據(jù)五次測量法的辨識值進行誤差補償后，半徑偏差分布范圍進一步減小。誤差補償實施以后效果顯著，機床的精度得到了有效的提升。這說明本研究所提出的誤差測量及辨識方法可準確量化擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸的運動誤差數(shù)值，較少的安裝次數(shù)提升了辨識結(jié)果的準確性。

4 結(jié)論

(1)運用多體系統(tǒng)理論和齊次坐標變換方法對幾何誤差進行表征，建立了擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸運動誤差測量模型。將旋轉(zhuǎn)軸的運動誤差在其相應的局部坐標系下進行表達，無需考慮機床的參考坐標系，符合運動誤差僅與旋轉(zhuǎn)軸自身制造精度相關，與軸間裝配精度無關的本質(zhì)特征。

(2)根據(jù)目前機床檢測精度高、速度快的要求，提出了一種基于DBB的五次安裝的擺頭轉(zhuǎn)臺型五軸機床旋轉(zhuǎn)軸運動幾何誤差測量、辨識方法。通過設置DBB的接觸球在測量坐標下的初始位置，保證旋轉(zhuǎn)軸相同初始安裝位置下的圓軌跡測量相繼進行，利用旋轉(zhuǎn)軸單獨運動以及直線軸聯(lián)動可直接實現(xiàn)一次安裝不同測量模式之間的切換，通過基于DBB圓軌跡測量的五次安裝，可實現(xiàn)兩個旋轉(zhuǎn)軸的12項運動誤差的全部辨識。減少了安裝次數(shù)，最大程度避免了安裝誤差對測量結(jié)果的影響，提升了測量效率。

(3)依據(jù)五次安裝法在擺頭轉(zhuǎn)臺型五軸機床上進行運動誤差辨識，利用辨識值實施誤差補償后，C軸的最低補償率達到15.85%，平均補償率為48.89%；B軸的最低補償率是26.45%，平均補償率達到51.49%，五軸同步運動形成的虛擬圓錐臺測量軌跡的半徑偏差降低了50.52%，誤差補償后機床精度得到顯著提升，說明本研究所提出的誤差測量及辨識方法對量化擺頭轉(zhuǎn)臺型五軸機床的運動誤差準確、有效。