基于滑模控制的自動泊車系統路徑跟蹤研究

姜立標 楊 杰

(華南理工大學機械與汽車工程學院, 廣州 510640)

0 引言

隨著科技的不斷發展，汽車智能化已經是當前必然趨勢。車輛作為一個復雜的非線性系統，隨著國內外學者的不斷研究，許多規劃方法和新型的控制方法被應用到泊車運動控制中[1-10]。

現有研究中，路徑規劃方法大多使用圓弧直線組合路徑，泊車路徑曲率不連續，沒有考慮車輛轉向能力。軌跡跟蹤控制器同時控制車速和方向盤轉角，一旦車速控制誤差較大會直接影響軌跡跟蹤效果。在對設計的路徑規劃方法和控制器進行仿真分析時，簡化的車輛運動學模型會造成實際控制器控制效果不佳。

本文以某SUV為研究對象，結合國內外自動泊車研究現狀，對路徑規劃方法中常見的曲率不連續問題進行研究，以解決規劃路徑曲率不連續、路徑規劃初始條件嚴格的問題，并提出基于B樣條曲線的路徑規劃方法和基于趨近律的非時間參考終端滑模路徑跟蹤控制方法。

1 車輛運動學模型

假設車輛泊車過程為低速運動過程，忽略車輪側向滑動,車輛在行駛中不出現側向力，基于阿克曼轉向原理建立車輛運動學模型如圖1所示。

圖1 車輛運動學模型Fig.1 Vehicle kinematics model

圖中，θ為車輛車身與坐標系X軸的夾角，φ為等效前輪轉角，l為車輛軸距，vf為車輛前軸中心點的速度，(xf,yf)為車輛前輪軸中心坐標，(xr,yr)為車輛后輪軸中心坐標。

為方便計算，將四輪車簡化為虛擬的兩輪車，如圖2所示。簡化后前后輪轉角的關系式為

cotα+cotβ=2cotφ

(1)

式中α——外輪轉角β——內輪轉角

圖2 等效前輪轉角示意圖Fig.2 Equivalent front wheel angle diagram

由實際條件可知，在滿足阿克曼轉向原理條件下，車輛方向盤轉角和等效前輪轉角之間存在近似線性的轉換關系

φ≈kφ

(2)

由目標車輛的實際測量結果可得k為16.2。

由假設條件可知，車輛運動學模型本身符合非完整性約束條件,即

(3)

由圖1可知

(4)

式(4)對時間求導得

(5)

將式(5)代入式(3),可得

(6)

又由圖1可得

(7)

將式(7)代入式(6)可得

(8)

聯立式(5)、(7)、(8)得

(9)

為簡化表達式，使用向量q=(v,ω)T表示車輛的線速度和角速度，其中，v為后軸中心點的速度，其方向垂直于后軸軸線。同時令

(10)

所以，對于前輪轉向的車輛，以后軸中點為參考點，其運動學方程為

(11)

車輛位姿可由后輪中點在坐標系中的位置以及車輛航向角來表示，可以描述為p=(x,y,θ)T。則車輛的運動學方程可以表示為

(12)

假設車輛最大等效前輪轉角為φmax，后軸中點最小的轉彎半徑為ρmin，ρmin=tanφmax/l，則對應的角速度為ω≤v/ρmin。

2 基于B樣條的泊車路徑規劃

常規泊車情況指車身方向與道路方向平行，與路基或是車庫方向沒有夾角。在實際泊車過程中，受駕駛經驗以及個人主觀因素的影響，駕駛員難以將車身方向調整至與道路方向完全一致，車身總會與道路方向存在一定夾角，傾斜車輛初始位姿更為常見，所以本文以傾斜車輛初始位姿為研究工況。

2.1 B樣條曲線

在實際工程應用中，曲線擬合可分為兩種：①曲線通過所有的樣本點，如三次參數樣條曲線和拋物樣條曲線等。②曲線不一定通過所有樣本點，只是較好地逼近樣本點。在兩種曲線中，考慮到局部修改的便捷性，方便設計者交互操作，第1種曲線不能滿足要求，第2種曲線多用于產品外形設計。因此Bezier提出了一種新的參數曲線表示方法，但Bezier曲線在實際應用中缺乏靈活性、控制性差、不易修改。為了克服上述問題，Shoenbery定義了B樣條曲線，其表達式為

(13)

式中Pi——目標曲線控制點

Ni,k(t)——B樣條基函數，是分段多項式

DeBoor和Cox定義的B樣條曲線基函數遞推表達式為

(14)

由式(14)可知，四階樣條曲線函數在其節點定義區間二階可導，能滿足泊車路徑中曲率連續以及曲率變化率連續的要求，因此在滿足方向盤轉角連續變化的約束下，為減少計算量，使用四階均勻B樣條曲線作為目標路徑的規劃基礎。根據樣條曲線基函數遞推公式，可求出目標曲線表達式，并將對應的曲線表達式寫成矩陣形式

(15)

將式(15)中控制點分解為橫坐標分量和縱坐標分量，即

(16)

2.2 運動學約束分析

(1)最大曲率約束

設計的路徑應該滿足車輛的等效偏轉角約束，其最大等效前輪偏轉角應該小于車輛允許的最大值，即

(17)

(2)速度約束

為避免車輛滑移等現象，泊車過程中的車速應該滿足低速運動的假設條件要求，即

|v|max≤|vmax|

(18)

(3)角速度約束

若參數超出實際車輛執行能力，使后續路徑跟蹤效果極差。設計路徑與等效偏轉角速度相關時參數應該滿足其角速度約束條件，即

|ω|≤ωmax

(19)

以控制點為變量，由B樣條曲線表達式求解路徑曲線，將泊車結束時車身與車位的夾角，即車身偏轉角最小化作為優化目標，結合車輛運動學約束、車輛機械結構約束以及環境約束等建立非線性約束方程。

3 軌跡跟蹤控制器設計

3.1 非時間參考路徑跟蹤系統誤差分析

現有軌跡跟蹤算法大多將期望軌跡視為時間函數，在時間域中求解控制律。這種控制方法常將車速作為控制量之一。但是在車輛行駛過程中，車速受到駕駛員、車輛狀態以及行駛環境等多方面的影響，如果因為特殊情況造成車速控制不佳，使得基于時間參考的控制律失去繼續跟蹤期望軌跡的能力，最終將造成泊車失敗。產生上述問題是因為時間相對于路徑跟蹤問題過于“自由”，與系統運行狀態無關，從而導致系統的規劃和控制不協調[11]。因此，基于非時間參考的控制思想被提出，通過引入其他非時間參考量代替時間參考量，提高系統在不確定環境中的路徑跟蹤能力。

基于非時間參考的路徑跟蹤控制律需要定義一個非時間參考的標量f，要求f為隨時間單調遞增函數，即

f=F(t)

(20)

(21)

設計的泊車路徑是一條與時間無關的空間曲線，不包含與時間相關的變量。車輛跟蹤目標路徑的過程可以描述為：對任意給定的幾何路徑S(x,y,θ)=0，尋找反饋控制律，對于任意給定的ζ>0，存在ft，當f>ft時，使|(xr,yr,θr)-(x,y,θ)|≤ζ成立，其中(xr,yr,θr)是參考的目標路徑坐標和車身偏轉角。

在車輛倒車狀態下，在建立的坐標系中選擇車輛實際路徑在X軸方向上的投影作為非時間參考量，即F=-x(t)，則車輛跟蹤目標路徑誤差如圖3所示。由圖3可得

(22)

則車輛路徑跟蹤誤差函數可以表示為

(23)

圖3 路徑跟蹤誤差Fig.3 Path tracking error

令pe=(ye,θe)，則其導數可表示為

(24)

假設車輛以穩定的車速運行，并且對目標路徑進行跟蹤，目標是在特定的有界等效前輪轉角輸入φ控制下，使得在任一的初始誤差下，系統能在該控制下pe=(ye,θe)有界并且不斷趨向于0，即

(25)

3.2 滑模控制器設計

為方便表示，令系統參考狀態量為

(26)

則系統狀態量導數可以表示為

(27)

將式(8)代入式(27)，可得

(28)

假設等效前輪轉角為小角度輸入，φ≈tanφ，令

(29)

則系統誤差狀態方程表示為

(30)

式中f(x)、b(x)——非線性函數

u——系統輸入

在普通滑模控制中，通常選擇一個線性的滑動超平面

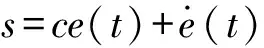
(31)

使得系統到達滑動模態后，各誤差漸近收斂為0，并且漸近收斂的速度可以通過選擇滑動平面參數矩陣任意調節，但狀態跟蹤誤差不會在有限時間內收斂為0。

為了提高控制器效果，提出終端滑模控制策略，通過引入非線性弧面，使得滑模面上跟蹤誤差能夠在有限時間內收斂到0。通過設計一種動態非線性滑模面方程實現終端滑模控制，切換函數為

(32)

其中p>q，p和q為正奇數，β>0。

基于滑模控制和終端滑模控制的非時間參考路徑跟蹤控制律都具備跟蹤目標路徑的能力，但對車身偏轉角狀態控制存在強烈的抖振現象，需提高趨近品質。結合采用趨近律的方法對趨近運動軌跡進行限制，改善趨近運動的動態品質。

根據趨近律滑模控制方法，采用一種新型趨近律滑模控制，令滑模面的導數為

(33)

其中

(34)

式中0<δ<1，η>0，ε>0 ，δ為fal(s,η,δ)在原點附近正負對稱線性段的區間長度，且fal(s,η,δ)為非連續函數。當|s|≤δ時，即s接近0時，式(33)第1項可以使得系統趨近速度變大，使得系統狀態在有限時間之內快速到達滑動面，同時在滑動面附近fal(s,η,δ)是光滑連續的，控制輸入的高頻震動現象被有效削弱。而且式(33)的第2項也是光滑連續函數，當|s|>δ時，能保證系統狀態以較大的速度趨近滑動面并且起到平滑和限幅的作用，聯立式(29)、(30)、(33)、(34)可得

(35)

定義Lyapunov函數

(36)

對式(36)求導并代入式(35)可得

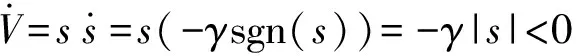
(37)

其中γ>0，因此可得

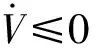
(38)

圖4 路徑規劃仿真結果Fig.4 Path planning simulation results

4 仿真驗證

在Matlab中輸入車輛的尺寸參數(表1)、車位信息以及初始位姿信息， 添加等式約束條件函數和不等式約束條件函數，在滿足約束條件下，令終止車身偏轉角最小為目標對控制點坐標進行優化求解，則結果就是滿足約束條件的B樣條曲線路徑的控制點坐標。

表1 車輛相關參數Tab.1 Vehicle related parameters

4.1 路徑規劃

結合實際泊車經驗，當車身傾斜程度過大時，駕駛員會自行調整方向盤使得車身偏轉角在一個合理的范圍之內，所以θ0不會太大，因此假設|θ0|∈(0°,5°]。查閱對應車型的技術手冊，可知最大允許曲率為0.256 4 m-1，最大允許角速度0.593 4 rad/s。

采用尺寸為6.4 m×2.0 m的車位作為目標車位，車輛起始位姿為x0=6.80 m，y0=1.80 m，θ0=0.087 rad。

由圖4a B樣條泊車路徑可知，規劃的曲線很好地連接了車輛起始點和預設終點，并且車輛在沿著規劃路徑行駛過程中，車輛輪廓沒有與道路邊緣、車庫邊界等發生碰撞，實現了車輛避障的要求。

由圖4b車身偏轉角可知，初始位置車身存在0.087 rad的初始偏轉角，但隨著規劃的泊車路徑，車輛在預設的泊車終點實現車身偏轉角為0 rad，滿足泊車的位姿要求，最大車身偏轉角為0.777 6 rad。

由圖4c泊車路徑曲率可知，在起始點處，由于車身有一定的偏角，規劃的路徑利用了該偏角，路徑起始點存在一定的曲率，該處的曲率與車身起始的偏轉角有關，路徑曲率最大值為0.236 8 m-1，小于最大允許曲率0.256 4 m-1，滿足車輛轉向約束條件。

由圖4d前輪轉向角速度可知，在起始位置處前輪需要迅速地滿足設計曲率的要求，因此需要較大的角速度，在整個泊車過程中，最大角速度為0.528 1 rad/s，小于最大允許角速度0.593 4 rad/s，滿足角速度約束。由上述仿真結果可知，此次規劃的路徑能實現車輛單步平行泊車。

4.2 路徑跟蹤

為驗證基于趨近律的終端滑模路徑跟蹤控制器的跟蹤效果，在Simulink上搭建路徑跟蹤仿真實驗。設定跟蹤路徑方程為y=16sin(0.05x)+5，車輛初始位姿參數為(0，0，0.02)，車速為1 m/s，3種路徑跟蹤控制器仿真結果如圖5所示。

圖5 3種控制算法路徑跟蹤效果對比Fig.5 Comparison of path tracking effects of three control algorithms

由圖5可知，終端滑模控制與非時間參考滑模控制相比，效果有所提升，在橫坐標約為-26 m處成功地跟蹤到參考路徑，車輛在轉彎較為劇烈地方的縱坐標跟蹤誤差減少；基于趨近率的終端滑模控制與基于終端滑模控制效果相近，但車輛在轉彎較為劇烈處縱坐標跟蹤效果更優，能更好地跟蹤到參考路徑。

由圖6可知，終端滑模控制與非時間參考滑模控制相比，縱坐標跟蹤最小誤差為-0.063 m，最大誤差約為-0.147 m，平均誤差為-0.105 0 m，系統的穩定平均誤差減少0.157 5 m，控制效果有明顯提升；基于趨近率的終端滑模控制與基于終端滑模控制效果相比，穩定誤差較小，最小誤差約為-0.069 m，最大誤差約為-0.144 m，平均誤差約為-0.106 5 m。

圖6 縱坐標跟蹤誤差效果對比Fig.6 Comparison of vertical ordinate tracking error

由圖7可知，終端滑模控制與非時間參考滑模控制相比，車身偏轉角跟蹤誤差最小誤差約為0 rad，最大誤差約為-0.044 rad，平均誤差約為-0.022 rad，約為-1.26°，控制效果相當，仍存在較強的抖振現象；基于趨近率的終端滑模控制與基于終端滑模控制效果相比，車身偏轉角跟蹤最小誤差約為-0.017 7 rad，最大誤差約為-0.023 2 rad，穩定誤差約為-0.020 5 rad，約為-1.174°，誤差范圍與前者相當。但系統車身偏轉角誤差的抖振現象明顯減弱，控制效果更優。

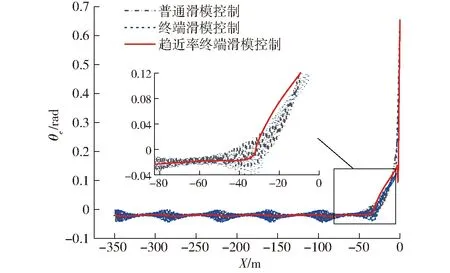
圖7 車身偏轉角跟蹤誤差對比Fig.7 Comparison of body deflection angle tracking error

實際泊車過程中，車輛一般從靜止開始運動到達目標車速，存在速度波動情況，為驗證設計控制器的適用性，設計車速從0 m/s加速到目標車速并且其過程中存在速度波動，對該情況進行仿真。目標路徑方程為y=16sin(0.05x)+5,車輛初始位姿參數為(0，0，0.02)，仿真時間為200 s。

圖8 不同車速路徑跟蹤仿真結果Fig.8 Tracking simulation results of different vehicle speeds

由圖8可知，在不同目標速度并且存在波動的情況下，基于趨近律的終端滑模路徑跟蹤控制器能跟蹤到目標路徑，不同速度下跟蹤情況相似，跟蹤效果受到速度影響較小，與車輛位置有較大關系，說明速度變化劇烈的情況下，本文設計的控制器仍具有較好的跟蹤效果。

對于相同的參考路徑，3種路徑跟蹤控制器都能控制車輛運動模型跟蹤到目標路徑。滑模控制結構簡單，但控制效果一般，系統相對穩定時，會存在較大的穩定誤差，并且車身偏轉角有較強的抖振現象；相比前者，終端滑模控制的控制效果有所改善，穩定誤差降低，但是車身偏轉角的抖振現象強烈，甚至還有所加強；本文設計的基于趨近律的終端滑模控制器不僅降低了穩定誤差，而且車身偏轉角誤差的抖振現象也明顯減弱，控制效果更優。

圖10 Simulink/CarSim聯合仿真結果Fig.10 Co-simulation result of Simulink/CarSim

4.3 Simulink/CarSim聯合仿真

在Simulink和CarSim中建立聯合仿真模型，包括路徑規劃、跟蹤控制、CarSim車輛模型S函數，仿真車速采用PID控制，不是本文重點，故不再贅述。聯合仿真流程如圖9所示。

圖9 聯合仿真流程圖Fig.9 Flow chart of co-simulation

結合日常泊車工況，設定期望車速為-1 m/s，x0=6.80 m，y0=1.80 m，θ0=0.087 rad。路徑規劃與跟蹤仿真結果如圖10所示。

由圖10a可知，在初始車身偏轉角不平行于車庫方向，車身偏轉角為5°的情況下，基于趨近律的終端滑模控制器能夠根據給出的參考路徑，控制目標車輛的方向盤轉角，使得車輛從起始位置到達目標位置。在路徑起始階段，車輛起始位姿與路徑起始處坐標以及該處切線方向一致，車輛能較好地跟蹤到參考路徑，當車輛停穩后，車輛與目標位置的縱坐標誤差為0.027 8 m。

由圖10b可知，車輛能夠跟蹤到參考路徑下的參考車身偏轉角，泊車結束時誤差為0.005 rad。

由圖10c、10d可知，在控制器控制下，當車輛到達預設位置后實現停車，不隨時間的變化發生移動。

由圖10e可知，在控制器控制下，縱坐標正向誤差最大達到0.031 m，負向最大誤差為-0.028 m，在此過程中，存在抖振現象，并且當泊車過程結束時，存在誤差0.027 8 m。

由圖10f可知，跟蹤過程中存在抖振現象，在x=5.72 m處，車身偏轉角正向誤差最大，達到0.045 rad，x=1.68 m處，車身偏轉角負向誤差最大，達到-0.038 rad，當泊車結束時，存在0.005 rad的偏轉角誤差。

由圖11可知，在CarSim仿真結果后處理部分中的動畫顯示中，控制的目標車輛能夠從初始位置較好地沿著參考路徑進入目標車位，從整體的輪廓圖可以看出，車輛與周圍的車輛沒有發生碰撞，在停車時沒有與后車發生碰撞，所以設計的參考路徑是合理的。

圖11 CarSim仿真動畫顯示Fig.11 Simulation animation of CarSim

5 結論

(1)結合B樣條曲線方法建立了非線性泊車路徑優化函數，并針對傾斜泊車起始位姿進行路徑規劃Simulink仿真，驗證了設計的路徑規劃方法具有較好的效果。

(2)結合非時間參考路徑跟蹤控制方法和終端滑模控制方法的優點，提出了基于趨近律的終端滑模路徑跟蹤控制方法。通過跟蹤目標正弦路徑的仿真實驗對比，驗證了設計的控制器具有較好的路徑跟蹤控制效果。

(3)建立了路徑規劃和基于趨近律的終端滑模路徑跟蹤控制器Simulink模型以及目標車型的CarSim整車模型，聯合仿真結果表明，本文所提算法路徑規劃結果滿足車輛泊車避障和運動約束要求，所設計路徑跟蹤控制器控制能較好地跟蹤參考路徑，快速安全進入車位。