視頻測量機器人星識別算法在自動天文定向中的應用

2019-03-06 08:12:18時春霖米科峰詹銀虎

測繪通報 2019年2期

葉凱，張超，時春霖,，米科峰,，詹銀虎

(1. 信息工程大學，河南鄭州 450001； 2. 61206部隊,北京 100042； 3. 61363部隊,陜西西安 710054)

傳統天文定向是通過觀測北極星實現的。然而，在北半球高緯度地區北極星所在高度角較高，不便于觀察；在低緯度地區或南半球，北極星容易被障礙物遮擋或地平坐標較低無法觀測[1]。因此有學者提出采用亮星識別定向，彌補北極星定向的不足[2]。當天空中云層較多時，亮星受遮擋無法觀測，因此考慮對任意星進行識別定向。

星識別是通過提取出觀測星的特征信息，利用星識別算法，在導航星庫中將其與星庫建立的特征信息進行匹配搜索，以此確定觀測星在導航星庫中的對應星體[3-5]。傳統基于廣角相機的大視場匹配識別算法存在不同程度的問題。基于三角形算法的星圖識別結果存在較多的冗余匹配，成功識別的難度較大[6-7]。文獻[8]通過主星選取法構建匹配三角形，利用約束性較高的星等過濾標準，進而識別星點。文獻[9]利用柵格圖像的處理思維，將星圖變換為稀疏矩陣進行識別。這些算法都沒有旋轉不變性，匹配錯誤率較大。而且，由于利用計算機仿真的環境、半物理仿真環境和太空中真實觀測環境差異較大，實際上，調研顯示某最新星敏器觀測的匹配成功率在90%左右[10]。另外，利用小視場的儀器觀測星體，根據其特征信息識別出該星，如亮星識別定向等利用傳統經緯儀、全站儀觀測方式[11-12]。這樣不僅需要相對較好的觀測環境，而且觀測時間較長，對作業員的體力和專業素質要求也較高，同時獲取的數據因觀測者狀態不同而存在誤差。為了消除該誤差影響，要求觀測員測前和測后在與測區緯度相近的基本天文點上進行誤差測定[13-15]。

針對上述傳統觀測北極星或亮星進行天文定向的局限，以及星識別方法冗余匹配量大和成功率低的問題，本文提出一種基于視頻全站儀對任意星觀測識別，實現自動天文定向的方法。視頻全站儀拍攝星圖具有小視場、單星性、形變小的特點，以TS50i全站儀為具體平臺，利用其視頻測量功能，在不同方位獲得小視場星圖數據，提取星點坐標信息，由星圖上的位置轉換到星點所在的實際位置。在獲取觀測星點高精度方位信息后，將星點高度角和兩兩星對之間方位夾角作為匹配元素，識別出滿足閾值條件的恒星，進而實現自動天文定向。試驗表明，該識別定向方法具有良好的準確性和精確性，可以滿足一等天文經緯度測量前的定向要求[13]。

1 星識別算法

1.1 觀測方法與恒星識別原理

本文采用視頻測量技術對恒星進行觀測。如圖1所示，利用視頻全站儀觀測時，首先通過肉眼找出恒星的位置，然后調整全站儀的方位，將其大致指向星體，使星體出現在視場中，最后利用全站儀視頻測量技術對其進行拍攝，獲得星體在相片上的坐標(x,y)。使用視頻全站儀的望遠鏡重復以上過程，分別大致指向觀測條件較好的3顆恒星，各連續拍攝10次左右，每次拍攝只需將星點成像在十字絲附近即可。記錄每次拍攝時刻T、水平度盤讀數H和垂直度盤讀數V，并獲取星點在全站儀上的成像圖。

連續觀測3顆星后，即可選取星的高度角及星對方位角差作為判斷條件完成星的識別。如圖2所示，對星si和sj觀測所得高度角為Vi和Vj，方位角差為Ai,j。在星表中進行搜索，如果星表中存在兩顆星si和sj，其解算高度角為Vi和Vj，方位角差為Ai,j，滿足閾值條件式(1)，則認為這兩顆星為匹配星。同樣的，可以選擇2顆星中的任意1顆與第3顆組成另一組匹配組合，按照上述方式進行匹配識別。

(1)

式中，wVi、wVj和wAi,j為高度角和方位角角差的誤差容限。利用測站位置和觀測時間解算的方位角為Ai和Aj，因此有

Ai,j=Ai-Aj

(2)

需要注意的是，對星si和星sj觀測時，測站水平度盤0°初始指向是未知的。設真北方向為A北,全站儀水平度盤0°初始指向為A0，測得星si的方位角值為Ai，星sj的方位角值為Aj，有

Ai,j=Ai-Aj

(3)

若某任意目標觀測方位角為Ai，即可得到其真實方位A如式(4)。識別定向過程實質上是在識別出對應星后，該星的真實方位信息便為已知，再由觀測數據反推求解A0。

A=A0+Ai

(4)

1.2 匹配閾值設置

匹配閾值設置的合理性直接影響匹配結果的正確性及匹配的效率。一方面，考慮觀測誤差對閾值設置的影響。由上文知，匹配是利用高度角和方位角差值作為篩選條件，而高度角和方位角的精度直接影響其匹配閾值的設定。觀測高度角和方位角的精度都受儀器測角誤差、觀測的偶然誤差的影響，而高度角還與大氣折射改正模型誤差有關[16-17]。匹配時只使用每顆星第一個時刻的觀測數據，偶然誤差作為匹配閾值的影響因素。對6顆已知星在已知測點上進行連續觀測，獲得已知星高度角與方位角的觀測值與理論值的差如圖3所示。

已知星的理論高度角和方位角是在已知測站上通過J2000依巴谷星表計算地平坐標得到，可以認為理論值為真值。觀測偶然誤差和測角誤差之和可以采用觀測值和理論值差值的內符合表示，誤差落在2倍中誤差的概率為95.45%。這里采用2倍中誤差作為觀測誤差和測角誤差的閾值取值，高度角2倍中誤差為6.35″。為了減少大氣折射對定向精度的影響，選擇高度角在20°～50°的星進行觀測[2]。在對數據進行大氣折射改正后，存在角秒級的誤差σ大氣，如圖3所示，其高度角差值中心偏離零點6.87″，由大氣改正殘余誤差引起。方位角觀測主要受儀器測角誤差和觀測偶然誤差的影響，其誤差分析可以借鑒高度角的評估策略。對方位角的觀測也可得到角秒級的精度，其2倍中誤差為5.95″。由此可知，任意星si的觀測高度角和方位角精度范圍如下式

(5)

另一方面，閾值選取要考慮解算高度角和方位角的誤差。作為匹配條件的理論高度角和方位角可由Novas程序解算得到[2]，在計算星表中待匹星的地平坐標時，需要給定測站的天文坐標。實際應用中，在任意測站點進行天文觀測，無法事先已知該點的天文坐標。目前衛星導航系統定位的精度較高，可以達到米級，且其定位結果容易獲取[18-19]，因此用該點獲得的衛星導航系統坐標替代天文坐標進行解算。同一測點的天文坐標和導航坐標之間存在垂線偏差，這樣必然會引入測站位置誤差，本文就測站位置誤差對匹配閾值設置的影響進行了討論。

作球面三角形如圖4所示，其中，點Z為天頂，點P為北天極，點σ為任意星，q為任意星的星位角，t為任意星時角，A為任意星的方位角，φ為測站的緯度，δ為任意星的赤緯，z為任意星的天頂距。

(1) 解算高度角誤差。由邊的余弦公式知

cosz=sinφsinδ+cosφcosδcost

(6)

式中，t=S-α+λ，其中S為測瞬的格林尼治恒星時，λ為測站的經度，α為任意星的赤經。

對式(6)微分得

-sinzdz=cosφsinδdφ-sinφcosδcostdφ-

cosφcosδsintdt

(7)

又有dt=dλ，且z=90°-V，因此有

cosVdV=cosφsinδdφ-sinφcosδcostdφ-

cosφcosδsintdλ

(8)

由第一五元素公式和正弦公式知

(9)

將式(9)代入式(8),有

dV=-cosAdφ+sinAcosφdλ≤|dφ|+|dλ|

(10)

再將測站緯度誤差Δφ和精度誤差Δλ代入式(10),可得

dV≤|Δφ|+|Δλ|

(11)

(2) 解算方位角誤差。由四元素公式知

(12)

對式(12)微分得

-csc2AsintdA+cotAcostdt=-sinφsintdt+

cosφcostdφ+tanδsinφdφ

(13)

又根據角的余弦公式和邊的余弦公式

(14)

將式(14)代入式(13)可得

(15)

又由式(9)的第二項正弦公式和式(15)得

(16)

由于觀測時選取高度角20°～50°之間的任意星，且dt=dλ，結合緯度誤差Δφ和經度誤差Δλ可得

(17)

解算任意星的高度角和方位角值如下

(18)

根據式(5)和式(18)可知

(19)

綜上分析，由式(1)、式(11)、式(17)和式(19)，可令

(20)

測站的天文坐標采用GNSS定位結果代替，試驗在登封某地完成。考慮登封的垂線偏差在角秒級，設Δφ=Δλ=10″，因此最終可令閾值的取值為

(21)

2 定向試驗和數據分析

選擇2017年9月17日夜晚，在登封某站點對多顆分布在360°方位上的任意星進行連續天文觀測。為了同時對定向的外符合和內符合精度進行評價，試驗借助新型野外天文測量系統獲取觀測數據。該系統包括具有視頻測量功能的TS50i全站儀、兼顧計時和定位功能的衛星導航系統天線，以及相關數據處理軟件。目前在北極星可見時，其定向精度較高，因此將北極星定向的結果作為外部檢核標準。試驗過程如下：

(1) 北極星定向觀測：將全站儀分別盤左和盤右連續觀測北極星6次，獲得精確的北極星定向結果。為避免儀器轉動時不穩定而造成測角誤差，每次觀測間隔大于1 s[20]。

(2) 任意已知星觀測：新型野外天文測量系統可以得到任意恒星過等高圈的時刻，以及過等高圈時的方位角。利用該系統自動尋星功能，對任意已知星分別連續拍攝10次左右。

(3) 重復步驟(2)，分別對多顆已知星進行連續拍攝。

本文提出的星識別算法具有良好的適用性，星識別成功率達100%。在對星等6.0以上亮度的星進行觀測時，可觀測數據較多，其中拍攝了分布在360°方位上的任意19顆已知星。在地平坐標下，根據式(1)的匹配條件，選擇每顆星第一個觀測時刻(即時號為1)數據對依巴谷星表進行匹配識別，匹配結果見表1。其中，該天文測量系統采用FK5系統的4065星表，根據已有的4065星表和依巴谷星表對應關系可知，該匹配結果完全正確。

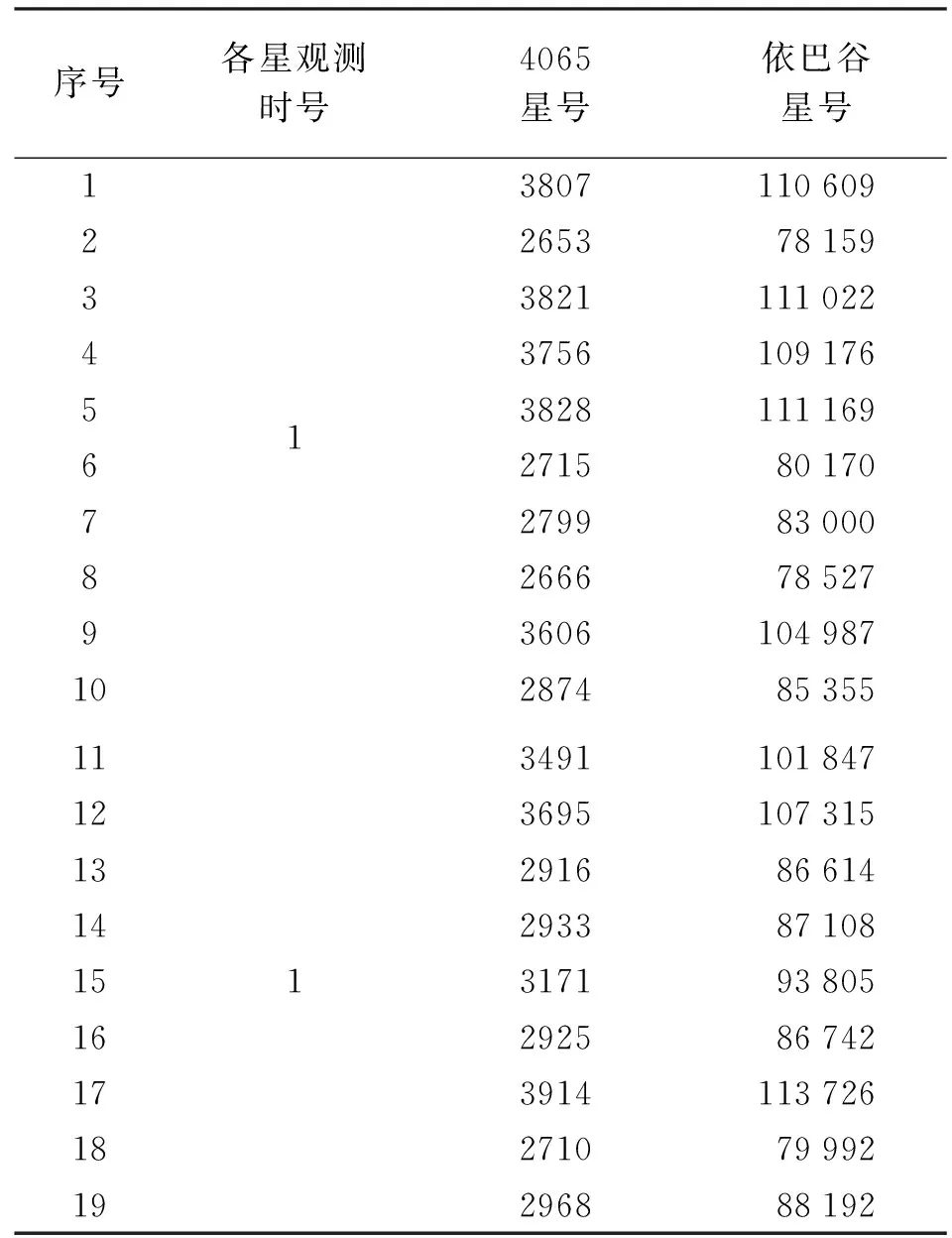
表1 星表匹配結果

在識別過程中，利用每3顆星之間的方位角和高度角信息進行匹配，每完成一組匹配時可以得到3顆已知星。利用該組星的多次連續觀測數據進行定向，即可得到一組定向結果。試驗中，選擇對19顆星進行匹配識別，由于在實際識別定向中，獲得某一組定向結果是隨機的，因此要對所有定向結果進行計算，可得到969組定向結果。

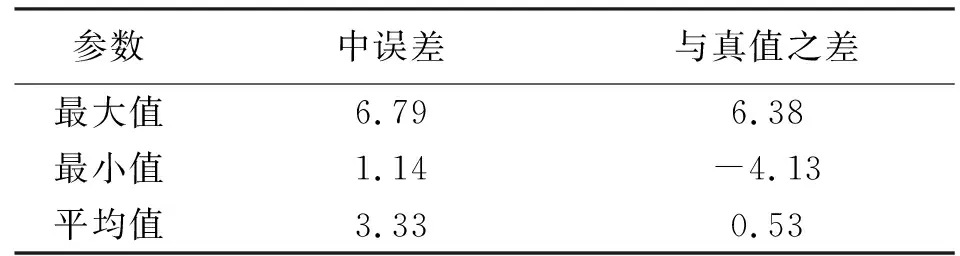
圖5、表2分別給出了任意星組的定向結果分布圖及誤差分布。可以看出，任意星組的定向結果中誤差為1.14″～6.79″，其平均值可達到3.33″。主要原因是單顆星觀測結果的內符合精度較高，然而不同星的觀測結果在真值上下分布，導致星組的平均值即定向結果偏向于真值，相應的，平均值相對各星整體結果的偏差會偏大。利用北極星定向結果作為真方位檢核該方法定向的精度，得知其與真值之差為-4.13″～6.18″，其中有73.3%的定向誤差集中在-2″～+2″，證明任意星組的定向結果普遍具有較高的精度。

天文測量規范要求一等天文經緯度測量前進行定向誤差不大于2′。由以上結果分析可以看出，該識別定向方法的定向誤差在角秒級，遠大于規范要求，筆者認為該識別定向可以滿足一等天文測量要求。

3 結論

面向自動天文定向的需求，基于視頻測量機器人平臺的工作特點，本文提出了一種基于高度角和方位角差值匹配的任意星識別定向方法。利用高精度測角數據，采用高度角約束可以較大地縮小閾值區間，從而有效地縮小匹配搜索范圍，消除冗余匹配，提高識別成功率。利用視頻測量功能，減少了每次將十字絲照準星體的過程，只需將望遠鏡大概指向星體，使星體出現在成像視場中即可，實現自動測量。試驗結果表明：

(1) 本文的星識別定向方法具有較高的星識別成功率和定向精度。試驗中觀測了任意19顆恒星，將其組成任意969組匹配星組，識別結果顯示所有匹配星組都能成功識別，實現100%的識別成功率。對全部969組的星組進行定向解算，可以得知其與北極星定向差值為-4.13″～6.18″，其中定向誤差在-2″～+2″之間的定向結果可占73.3%，可以滿足一等天文經緯度測量前對定向的要求。

(2) 本文的星識別定向方法具有較強的生存能力。相對以往采用北極星定向和較亮的恒星定向方法，該方法觀測時更不易受天氣條件的限制，在多云天氣也有較好的適用性，理論上只需存在3顆以上可觀測恒星即可完成匹配識別定向，既可以解決在緯度較高或較低及南半球地區采用北極星定向誤差較大或無法觀測的問題，又可以解決天空中較亮的星被云層遮擋而無法觀測的問題，利用視頻測量功能，通過恒星識別進而實現自動天文定向。

(3) 本文的星識別定向可以滿足一等天文經緯度測量前定向的要求。在實際應用中，目前某野外天文測量系統在自動尋星前采用北極星定向，其定向過程采用人眼瞄準目標，且觀測受天氣的影響，該識別定向方法可以很好地彌補系統的不足，作為其定向的替代方式，提高天文測量自動化水平。