融合多特征信息的密集場景人群分群檢測算法

吳福豪, 趙 倩

(上海電力學院 電子與信息工程學院, 上海 200090)

隨著世界范圍內城市化進程的不斷推進,人群聚集現象變得越來越突出,如體育比賽、游行示威、恐怖活動等,密集人群中小群體檢測技術在智能監控、虛擬現實、公共安全等方面的應用也越來越普遍。通常情況下,在一個群體中有50%～70%的人是以小群體的形式行動[1],故人群中個體之間的相互作用對于群體現象的研究十分重要[2]。然而,由于人類的社會性,人群中的相互作用不僅發生在個體與個體之間,而且也發生在各個小群體之間,所以密集人群中小群體檢測也受到越來越多的關注。

密集人群的運動場景從宏觀上可以分為兩種類型——結構化的運動場景和非結構化的運動場景[3]。在結構化的運動場景中,人群運動發生在共同的路徑上,運動路徑不會頻繁發生變化,并且場景中的每個空間位置都有一個關鍵的群體行為,例如公路自行車賽、馬拉松比賽等。在非結構化擁擠的場景中,行人在不同的方向上自由移動,每個空間位置往往有幾個群體行為。此外,人群之間由于存在遮擋等復雜的相互作用,進一步增加了在非結構化運動場景中對人群分割的難度,而本文將在非結構化的密集運動場景中進行群體檢測。

在基于群組的方法中[4],擁擠人群具有高噪聲或高復雜度的特點,小群體被認為是組成人群的基本要素,就導致有一部分個體難以區分。識別群體是掌握人群中復雜的社會動態和規范集體行為的重要步驟[5],就給計算機視覺帶來了新的挑戰,因為群體比單個個體或整個人群來說更難以表征。

目前,有些算法是通過物理模型(例如流體力學[6])來分析人群特性的。此類算法在極其密集的人群中有效,但由于其忽視了單個個體的主觀目的和目標,因而具有一定的局限性。 文獻[7]提出了行人動力學的社會力量模型,認為任何朝向目標移動的行人都會受到周圍行人的影響。文獻[8]認為社會關系會影響人們在人群中的行為方式,強調大多數人傾向于團體活動。這些算法都是通過由空間鄰近性和速度特征的組合來定義社會學群體間的親密度,從而逐次合并小群體。本文結合了軌跡時空特征[9]、個體運動方向特征[9]、格蘭杰因果性特征[10]、熱能圖特征[11-12]以及個體之間運動相關性特征[12],將對群體的檢測視為有監督的相關性聚類[13],采用結構支持向量機(Support Vector Machine,SVM)對提取的特征進行訓練分類[14-15]。為了保證算法的魯棒性,試驗采用的數據集均為現實場景中的視頻圖像。

1 相關性聚類

一個群體,可以被定義為兩個或兩個以上的人員,根據物理身份(空間鄰近性)和社會身份(小群體內規則)達成共同目標并共享成員。

首先,將群體檢測作為一個聚類問題進行處理,以獲得各特征的權值。將一組行人編號為P={a,b,…},設函數Y(P)作為解決這個聚類問題的所有可能出現的方案。那么當a∈P,?y∈Y(P)且∪y∈Y(P)y=P,y={y1,y2,y3,…}為一系列有效解。

相關性聚類算法將權值矩陣Wab作為輸入。對于一個確定的|Wab|,當Wab>0時,行人a和行人b屬于同一個小群體;當Wab<0時,行人a和行人b不屬于同一小群體。因此,需要將同一聚類y中元素對的總和最大化

(1)

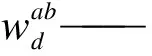
將W中的成對元素親和度參數化為有界不相似度量權重的線性組合及其補充

(2)

式中:α,β——參數;

d(a,b)——組合特征。

根據不同場景的不同聚類規則,式(2)中的參數W=[α,β]保證了每個特征在識別群組時所占的比重有所不同。對于最佳參數W的選擇受到文化、社會環境以及場景天氣等諸多因素的影響,故采用學習框架來得到最合適的聚類規則。

2 特征提取

本文算法設計了5個特征,分別為軌跡時空距離特征d1,運動方向特征d2,格蘭杰因果性特征d3,熱能圖特征d4,運動相關性特征d5,用來捕捉運動行人的物理和社會身份,以及識別他們之間存在的共同目標。因此,兩個成對的行人特征向量定義為

d(a,b)=[d1,d2,d3,d4,d5]

(3)

2.1 軌跡時空距離特征

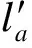
(4)

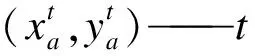
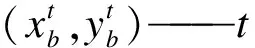
然后定義

(5)

式中:Na,Nb——行人a和行人b在時間窗T內的圖像中出現的次數。

2.2 運動方向特征

在無序運動的人群中,一個小群體內的行人往往會有一個共同的目的地,因此他們的運動方向在通向目的地的過程中會基本保持一致。

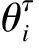
(6)

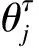
(7)

2.3 格蘭杰因果性特征

(8)

如果式(8)成立,則說明行人b對行人a的運動軌跡產生了影響。

引入約束和非約束模型的殘差平方和分別為

(9)

(10)

式中:n——分析圖像的總幀數。

定義測試統計為

(11)

本文采用 Fisher-Snedecor分布來計算格蘭杰因果性特征,故

d3(a,b)=

(12)

2.4 熱能圖特征

在不同的位置,小群體的形成和散開對于群體檢測來說也是一個非常有效的信息,因此采用熱能圖來描述群體活動成為一個十分有用的特征。當軌跡穿過一個區域,這個區域將被定義為一個區域熱源。通過這種方式,軌跡可以被轉換成一系列熱源。此外,為了進一步捕捉軌跡的時間信息,在不同的熱源上引入衰減因子,使得“較早的”熱源(即離軌跡起點較近的小塊)的熱能較小,而“較新的”熱源將具有較大的熱能。

假設在當前的分組中,軌跡la的熱源區域Ru1×v1的能量衰減為

(13)

式中:u1,v1——區域的長和寬;

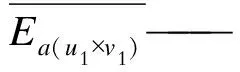
e-kt·tint——衰減周期;

kt——衰減因數;

tint——行人a在熱源區域的時間。

當軌跡la由路徑(p,q)進入熱源區域Ru1×v1在相關網格(u,v)處熱源開始激發,其熱源衰減過程Ha(u,v)為

(14)

式中:ks——在不同路徑、不同距離下的重要性參數;

(p-u),(q-v)——軌跡la由路徑(p,q)進入熱源與網絡(u,v)的距離。

把每一個軌跡都構建熱能圖,其熱能圖特征可表示為

(15)

2.5 運動相關性

如果行人a和行人b屬于同一小群體,則其運動軌跡一致,表明兩人的運動相關性比較高,從t→t+1時刻,行人a和行人b的運動相關性可表示為

(16)

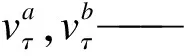
3 結構化SVM

本文采用結構化SVM來模擬和學習預測解決方案。SVM是一種監督式機器學習方法,用于分類和模式識別等。在該方法中,支持向量被用來表示決策邊界,并將低維輸入空間的線性不可分數據映射到高維特征空間,使其線性可分離。該算法將在第i個時間窗口所有可能兩兩成對的行人軌跡所提取的特征作為輸入xi,xi={[1-di(a,b);di(a,b)]},yi為人群分類結果。構建一個由輸入到輸出的分類映射,輸入輸出對為{(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)}。根據相關性聚類算法獲得Wd,然后經過Frank-Wolfe算法迭代300次得到最優權值W[15]。由判別函數F測量(x,y)對之間的兼容性,并為那些良好的匹配給出高分。判別函數為

(16)

通過最小化一個凸目標函數,參數可以通過一組實例{(x1,y1),(x2,y2),(x3,y3),…,(xn,yn)}在大范圍框架中學習。凸目標函數為

(17)

其中:?i:εi≥0;?i,?y≠yi:WTδφi(y)≥Δ(y,yi)-εi;δ(φi(y))=φ(xi,yi)-φ(xi,y);Δ(y,yi)為損失函數。

4 損失函數

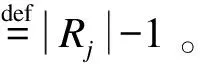
(18)

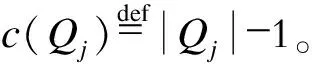
(19)

由給定精確度P,召回率R和F1-score將損失函數定義為

Δ(y,yi)=1-F1

(20)

試驗算法流程如圖1所示。

圖1 算法流程示意

5 試驗結果

本文在MPT和GVEII數據集上進行測試,數據集MPT和GVEII主要包括來自公共場所攝像機拍攝的不同場景條件下大量行人活動的視頻(取4個群體典型視頻)。算法使用MATLAB軟件實現,試驗均在Intel i5 CPU,4 G RAM下進行。將本文算法與文獻[16]算法進行對比,結果如表1所示。

表1中,場景1為數據集GVEII中的一個室內場景,場景2為MPT中街道交叉口場景,場景3為MPT中機場內的場景,場景4為MPT中馬路上的場景。

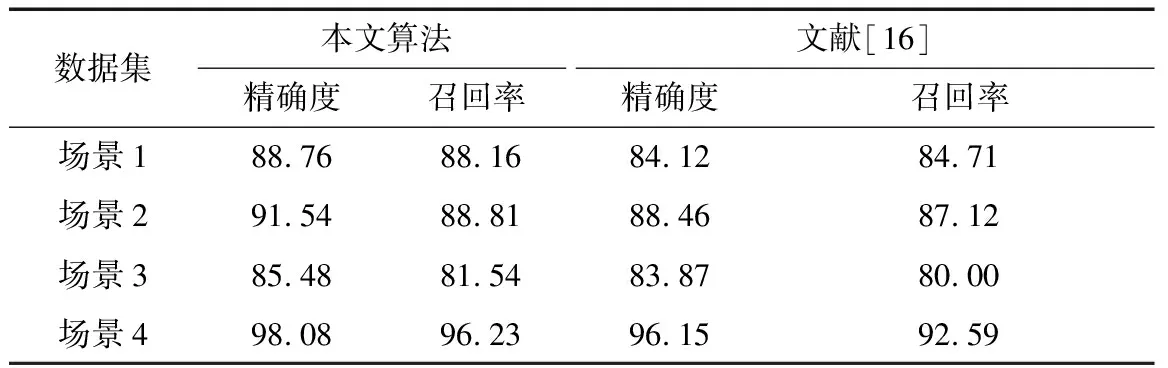
表1 兩種算法的測試精確度對比 %

由表1可知,本文算法的精確度和召回率均高于文獻[16],故在分割個體和小群體方面,本文算法要優于文獻[16]的算法。

將參數W=[α,β]=[w1,w2,w3,…,w10]代入式(2),得

(21)

每個特征占分群得分的比例由式(21)中的常數項決定,其編碼為特征本身系數的絕對值。

圖2為式(21)中特征歸一化的系數。

圖2 式(21)中特征歸一化的系數

由圖2可知,在任何一個數據集中,軌跡時空距離特征都占有最高比重,其他特征的重要性隨著視頻序列的改變而有所變化。例如,在場景1和場景3中,運動方向特征在測量分群算法得分時起重要作用,而場景2中,運動方向特征所占比例極小。運動相關性特征在場景2和場景3中十分重要,但在場景1和場景4中熱能圖特征的關鍵性更高。

圖3為不同場景分組檢測結果對比。圖3中,第一列為本文算法試驗結果,第二列為文獻[16]試驗結果。根據已知分組情況,在場景1中,本文算法正確分組6個,錯誤分組零個;文獻[16]算法正確分組5個,錯誤分組1個。在場景2中,本文算法正確分組10個,錯誤分組2個;文獻[16]算法正確分組9個,錯誤分組5個。在場景3中,本文算法正確分組5個,錯誤分組3個;文獻[16]算法正確分組5個,錯誤分組3個。在場景4中,本文算法正確分組3個,錯誤分組零個;文獻[16]算法正確分組2個,錯誤分組零個。由此表明,本文算法的分組情況在整體上優于文獻[16]算法。

在密集度較小的場景中,行人運動軌跡受同一組行人運動影響較大,文獻[16]中的軌跡相似性特征對行人分組十分有利。但在密集度較大的場景中,一個人的運動軌跡不僅受到同一組行人的影響,而且也受到周圍多個行人的影響。因此,文獻[16]中的軌跡相似性特征在密集度大的擁擠場景中會使錯誤分組的情況增多。

圖3 不同場景分組檢測結果對比

本文算法通過連續能量最小化的方法提取了行人的坐標和軌跡信息[17]。在現實場景中,經常有不精確的地平面投影或跟蹤誤差,會造成定位行人坐標誤差。由于自動人體檢測器的定位誤差會產生許多軌跡碎片,當計算軌跡時空距離特征和格蘭杰因果性特征時,大量的軌跡碎片會影響群體檢測的效果。因此,通過減小窗口的大小,可以最小化每個例子中的分割軌跡的數量,并恢復大部分軌跡的原始效果。

5 結 語

在無序運動的場景中,人群不僅有空間性特征,而且還保留有社會特征,因此本文提取了個體之間運動軌跡時空特征、運動方向特征、格蘭杰因果性、熱能圖特征以及運動相關性特征來捕捉和表征不同群體的特性。為了得到有效的聚類規則,采用了結構化支持向量機。該算法綜合了各個物理特征和社會特征,最大程度地利用了群體中的有效信息,使得分組更為精確。經過試驗結果比較可知,本文的檢測效果要高于文獻[16]的算法。