一種基于桶重構的差分隱私直方圖發布方法*

徐文濤 ， 李林森 ，鈕佳超 ， 張凌軒

（1.上海交通大學 網絡空間安全學院，上海 200240；2.國防大學 政治學院，上海 200433； 3.上海市信息安全綜合管理技術研究重點實驗室，上海 200240）

0 引 言

進入21世紀，隨著互聯網的快速發展，應用信息技術的出現和不斷普及，各種數據庫應用系統存儲了大量數據。這些數據擁有巨大的社會價值，可以用于資源分配、醫學療法評估、了解疾病的傳播和改善經濟效用等。對于科研機構、企業以及政府統計部門而言，數據是非常有價值的資源。對這種資源強烈的需求，也大大推動了人們對數據的收集、儲存、分析和分享。然而，許多數據中往往存在著一定的隱私信息，如果不采用適當的隱私保護技術而直接發布數據，很容易造成個體隱私信息的泄露[1]。

近年來，國內外頻頻出現隱私泄露事件，給個人、家庭和社會造成了一定恐慌，如2018年8月爆出的華住酒店集團數據泄露事件。據媒體報道，有人在境外兜售華住旗下酒店的開房記錄，涉及共計約5億條公民個人信息，有1.3億個身份證信息，在社會上造成了極壞影響。為了有效保護個人隱私，近年來出現了許多隱私保護模型，如k-匿名[2]、z-多樣性[3]和t-鄰近性[4]等。然而，這些典型的隱私算法在定義時都局限了攻擊者的背景知識，且只針對特定的攻擊模型才有效。而在實際操作中，攻擊者擁有的背景知識遠遠超過其假設，他們只需要通過細致的推理，就可以攻擊到用戶的個人隱私信息。

為了能夠定量地控制隱私信息的泄露，盡量使隱私保護方法不依賴于攻擊者的背景知識，2006年微軟研究院的德沃克（Dwork）與卡瑪利拉（Kamalika）等人提出了差分隱私保護模型[5]，通過向查詢結果或分析結果中添加噪聲來達到更強的隱私保護。

基于直方圖結構的數據發布方法是目前最常用的一種數據發布方法。由于它形象地顯示了數據分布形式，因此其統計結果可以為實現計數范圍查詢提供理論依據。在直方圖發布過程中，為了滿足差分隱私并提高數據發布的準確性，通過重新劃分桶的思想，合并原始直方圖鄰接相似的桶進行重構，并添加拉普拉斯噪音來滿足差分隱私的要求。然而，針對原始直方圖中存在離群點的情況，會產生較大的全局敏感性。直觀來講，離群點是在數據集中偏大或偏小的值，也可以說離群點與數據集中其他值差的絕對值要遠遠大于普通值之間差的絕對值。例如，在統計身高的數據集中，高于2 m的人群就是一個相對非常小的計數值，即一個典型的離群點。現有的針對此類數據集的差分隱私直方圖發布算法雖然可以保證數據發布的精度，但是執行效率不高。因此，針對此類攜帶離群點的數據集，在保證發布數據質量和可用性的前提下，設計出高效的差分隱私直方圖發布算法具有重要的意義。

1 相關工作

差分隱私保護模型提出后，迅速引發了各個領域的研究熱潮。目前，國內外對差分隱私的研究主要集中在兩個重要領域，即數據分析和數據發布，而差分隱私研究的核心問題是如何實現滿足差分隱私要求的數據發布。一個實現差分隱私發布機制的是文獻[6]提出的拉普拉斯（Laplace）機制。該機制主要通過向確切的查詢結果中添加服從拉普拉斯分布的獨立噪聲來擾動真實的查詢結果。文獻[7]中提出一種叫做PMW（Private Multiplicative Weights）的發布機制。PMW機制主要結合差分隱私保護技術與機器學習中的加權多數算法（Weighted Majority Algorithm），通過投票機制構建了一個復合算法。

近年來，一些學者在差分隱私直方圖發布研究領域取得了豐碩的研究成果。最早的差分隱私直方圖發布方法是德沃克提出的LP（likelihood procedure）方法[6]。為了提高發布數據的準確性，文獻[8]提出了基于后置噪音優化處理的差分隱私直方圖發布方法Boostl，采用樹結構代表一個查詢序列，其中樹中的每個節點代表一個計數范圍查詢，最后通過一致性約束后置處理技術對添加噪音后的樹節點進行求精處理。為了響應較長范圍的查詢，東北大學的許等人在文獻[9]中提出了NoiseFirst方法和StructureFirst方法。NoiseFirst方法采用動態規劃技術，通過合并鄰近相似桶的方法，對LP產生的等寬直方圖進行重構；而SructureFirst方法的思想是先對動態規劃技術產生的優化直方圖的桶邊界進行微調，形成不等寬的直方圖，然后向每個桶中添加適當的噪音，形成滿足差分隱私的直方圖。雖然該方法降低了噪音誤差，但是產生了新的重構誤差。為了平衡噪音誤差和重構誤差，加拿大康科迪亞大學的陳等人[10]提出了采用自頂向下層次聚類的方法動態尋找最佳合并后的桶個數k。實驗證明，這種方法在時間效率和數據發布準確性上，較StructureFirst方法都有顯著提高。

本文針對差分隱私直方圖發布方法中原始直方圖存在離群點的問題，提出一種差分隱私保護下攜帶離群點的直方圖發布的R-G-I方法。該方法在實現差分隱私保護直方圖發布數據的基礎上，有效地解決離群點存在的問題。此外，通過實驗與同類算法的對比，證明了本文所提方法在保證發布數據質量和可用性的前提下，在準確性上具有明顯優勢。

2 基礎知識與相關定義

定義1 差分隱私（Differential Privacy）[6]：假設有相鄰數據集D1和D2（若有數據集D1和D2，其差別除了最多相差一條記錄外，結構與屬性都相同，那么稱D1和D2為相鄰數據集），隨機算法A的值域為dom(A)，該算法的任意輸出O∈dom(A)，如果滿足Pr[M(A)∈S]≤eε×Pr[M(A*)∈S]，就稱算法A滿足ε差分隱私。隱私披露風險由函數A決定。其中，Pr[·]表示算法隨機性輸出的概率，ε為差分隱私預算。參數ε用于衡量隱私保護的強度，大小由使用者設定。更小的ε表示需要添加幅度更大的噪聲，從而帶來更強的隱私保護。顯然，差分隱私保護強度與發布數據的可用性之間是一對矛盾。一般地，ε是一個接近于1的公開實數，通常取值為0.01、0.1、l、ln2和ln3等，也可根據實際需要取值。

差分隱私保護主要有兩種機制——Laplace機制和指數機制。本文主要使用Laplace噪聲機制，將其分別應用于數值和非數值數據。因此，主要介紹Laplace噪聲機制。Laplace機制主要是通過服從Laplace分布的噪聲將其應用于隱私數據的保護，從而干擾真實輸出結果來實現差分隱私保護。

定義2 Laplace機制：給定一個數據集D和一 個 查 詢 函 數f∶D，其 中γ～Lap(Δf/ε)為 隨 機 噪聲，敏感度為Δf，則滿足ε-差分隱私的隨機算法A(D)=f(D)+γ，服從參數為Δf/ε的拉普拉斯機制[6]。

在拉普拉斯機制實現差分隱私算法的過程中，注入的噪聲分量Lap(Δ/ε)的樣本分布與算法敏感度Δ和隱私預算ε參數密切相關。算法敏感度是衡量一個算法針對不同輸入數據時算法輸出的變化程度，而隱私預算ε是基于差分隱私模型擬定的一個用來指示隱私保護級別或程度的一個數據量。包含n個單元桶的直方圖，實際上就是n個獨立的范圍計數查詢。假設其中一個單元桶的頻數值為X，從數據集中刪除一條記錄后該桶的頻數值為X′，那么||X-X′||=1，則直方圖每個桶的計數查詢敏感度Δf=1。通過向直方圖每個桶的統計頻數中注入少量服從拉普拉斯分布的獨立噪音，就可以滿足差分隱私的要求。

直觀來說，離群點就是在數據集中明顯偏大或偏小的少數值。也可以說，離群點與數據集中其他值差的絕對值要遠遠大于普通值之間差的絕對值。例如，對于一個頻數序列H={19,6,300,28,13}，直覺告訴人們300為該序列中的離群點。通過計算也很容易發現，300與其他頻數差的絕對值要比其他頻數之間差的絕對值大很多。因此，考慮采用比較數值之間差值的關系，來形象定義離群點和交替分布度等概念。

3 差分隱私直方圖發布算法

3.1 問題描述

直方圖是一種有效的統計報告圖，采用一系列高度不等的桶來表示相應查詢范圍內的統計信息情況。令A表示數據表E中的某一個屬性，a∈A為屬性A中的任一屬性值，count(a)代表數據表中屬性值為a的記錄個數，則直方圖為一系列統計屬性值個數的計數序列。每個計數值代表直方圖相應桶的頻數，用頻數序列H={H1,H2,…,Hn}表示，其中為數據表中的記錄個數。任何一個數據表都可以根據某個屬性映射成相應的直方圖。

在直方圖發布過程中，為了滿足差分隱私并提高數據發布的準確性，通過重新劃分桶的思想，合并原始直方圖鄰接相似的桶進行重構，并添加拉普拉斯噪音來滿足差分隱私的要求。本文在相關工作中提到的目前基于差分隱私的直方圖發布，主要有NoiseFirst方法、StructureFirst方法和P.HPartition方法等。然而，這些方法在重構過程中都忽略了原始直方圖頻數中存在離群點的問題。原始直方圖中存在離群點的情況會產生較大的全局敏感性，且由于原始直方圖的鄰接桶頻數相差過大，很少有相似的桶相互合并，這就失去了重構的意義，因此分析離群點十分必要。

這里引入以下四個定義[11]。

定義3 標準梯度值：給定一個數據集D和一個原始直方圖H，是它的有序頻數直方圖，記集合則D的標準階梯特征值L=count(U)+1。其中，count(U)表示集合U中元素的個數，δ為離群長度。

定義4 實際梯度值：在原始直方圖H={H1, H2,…,Hi,…,Hn}中，仍 記 集 合U={i||Hi-Hi-1|}＞δ，且M=count(U)+1，則稱M為實際階梯特征值。

定義5 交替分布：對于一個原始直方圖H，如果M=L，則稱該原始直方圖滿足均勻分布；如果M＞L，則稱該原始直方圖滿足交替分布。

定義6 交替分布度：給定一個原始直方圖H，如果它的標準階梯特征值為L，實際階梯特征值為M，則定義H的交替分布度為ADD=M-L。

例如，對于一個給定的原始直方圖H={31，15，14，34，12，3，16}，設δ=10，那么H的標準階梯特征值為3，而實際階梯特征值為6，則H的交替分布度ADD=6-3=3。交替分布度是原始直方圖的固有屬性，定量地刻畫了該原始直方圖離群點的分布狀態。交替分布度越大，表明原始直方圖中離群點個數越多，分布得越分散，原始直方圖總體分布越不均勻。離群點會產生很大的全局敏感性，離群長度δ越大，誤差值越大，且隨著離群點個數的增多，會使原始直方圖形成階梯分布特征，即原始直方圖成交替分布。隨著交替分布度的增大，對誤差的影響也越大，即使現存的高效率重構方法也很難對這類原始直方圖進行有效重構。總之，無論是離群點還是交替分布對直方圖重構的影響，最根本的解決辦法是降低交替分布度，使序列回歸原始梯度。

3.2 基于桶重構的差分隱私直方圖發布方法（R-G-I方法）

為了解決原始直方圖中存在離群點的問題并提高數據發布精度，將差分隱私方法引入直方圖發布。這種方法是在桶重構的基礎上實現的，記為R-G-I分布法。在后文中將對該方法的有效性和準確性進行驗證，下面對該方法的操作步驟進行簡單介紹。

（1）將隱私預算參數ε劃分為兩部分，一部分記為ε1，一部分記為ε2。其中之一在步驟（3）中使用，使用貪心算法對相似的桶進行選擇并做合并處理；另一部分在完成重構后，將拉普拉斯噪聲加于直方圖桶中。

（2）借助調用梯度回歸算法（Gradient Regression）對原始直方圖的頻數序列進行滿足差分隱私的排序預處理，從而降低原始直方圖中離群點的影響；

（3）通過調用合并相鄰桶的貪心算法（Greedy Algorithm），對進行預處理后的原始直方圖進行桶重構處理，并用紅黑樹優化桶重構的過程；

（4）向經過步驟（3）處理后直方圖的桶頻數中添加適量的獨立噪聲進行擾動；

（5）向直方圖的桶頻數調用保序回歸算法（Isotonic Regression）提高發布精度。

該方法主體為三個依次執行的算法，分別為梯度回歸算法（Gradient Regression Algorithm）、合并相鄰桶的貪心算法（Greedy Algorithm）和保序回歸算法（Isotonic Regression Algorithm），取三個算法的關鍵詞英文首字母，簡稱該方法為R-G-I發布方法。下面對R-G-I發布方法的三個算法進行詳細介紹。

3.2.1 梯度回歸算法（Gradient Regression）

下面對梯度回歸算法進行介紹。

算法1：Gradient Regression(H,δ,ε)

輸入：原始直方圖H={H1,H2,…,Hn}，δ，ε//δ為離群長度參數

輸出：滿足均勻分布的原始直方圖H′={H1′,H2′,…,H′n}

步驟：

（1）對原始直方圖H={H1,H2,…,Hn}進行升序 排序；

（2）對原始直方圖的交替分布度ADD進行準確計算；

（3）分析ADD的值，若大于0，則對原始直方圖的前n-1個頻數進行計算和檢驗，當(Hi+Lapi(1/ε))-(Hi+1+Lapi+1(1/ε))＞0時，需要將相鄰兩個H進行交換；

（4）繼續重復執行上述步驟（3），當相鄰兩個H不能交換時停止；

（5）原始直方圖H′={H1′,H2′,…,H′n}滿足均勻分布的情況下將其返回；

（6）否則，直接給出原始直方圖H={H1,H2,…, Hn}。

例如，原始直方圖為H={31,15,14,35,12,1,17}，其中設定δ=10。由于原始直方圖H的ADD=3，通過算法1的計算結果為H′={1,12,15,14,17,31,35}，此時H′的ADD值等于0，實現了交替分布度減少的目標。對相鄰的桶頻數進行加噪處理是梯度回歸算法的重要步驟，而不是直接對真實的桶頻數進行排序。以差分隱私條件為基礎，如果原始直方圖滿足差分隱私所規定的條件，則可以對其做一個近似排序，輸出結果以真實桶頻數進行。因此，在排序過程中，隱私預算并不參與其中，也不會消耗。算法1中，進行直方圖頻數排序過程中，即使情況最差，對應的時間復雜度最大為O(n2)。所以，算法1的時間復雜度為O(n2)，其中n為原始直方圖中桶的個數。梯度回歸算法通過降低ADD的值，最大程度地降低了離群點對直方圖重構的影響。

3.2.2 合并相鄰桶的貪心算法（Greedy Algorithm）

在進行直方圖發布時，對相鄰近似的桶進行合并處理，以差分隱私技術為基礎，適當加入拉普拉斯噪音，從而提高數據發布的準確性。設原始直方圖H={H1,H2,…,Hn}，有一個包含k個桶的桶劃分方案H*={B1,B2,…,Bn}中，每個桶Bj=(lj,rj,cj)，其中lj為每個桶的左邊界，rj為每個桶的右邊界，每個桶所賦予的值用cj表示，其值可以取前j個桶的頻數之和的平均值。設有k個不同的桶和序列H={H1,H2,…, Hn}，將這些序列分別裝入這些桶中，裝入時序列的元素要滿足{Hi|lj≤i≤rj}。可以看出，如果桶劃分策略不同，那么分布數據將會有不同的結果，進而產生不同的誤差。為了詳細分析誤差，定義桶劃分的誤差。

定義7 桶劃分誤差：設H={H1,H2,…,Hn}為原始直方圖，H*={B1,B2,…,Bn}為桶劃分方案，桶劃分以劃分方案為準，將劃分后的直方圖序列記為H′={H1′,H2′,…,H′n}。由于H′和H之間存在誤差，因此將這種誤差記為Error(H*,H)，也就是桶劃分誤差。

由于上述誤差有正有負，因此為了比較不同桶劃分方案的合理性，需要對誤差平方處理，最終以平方和誤差（SSE）表示。對于每個桶，誤差用Error(Bi)表示，相應的計算公式為：

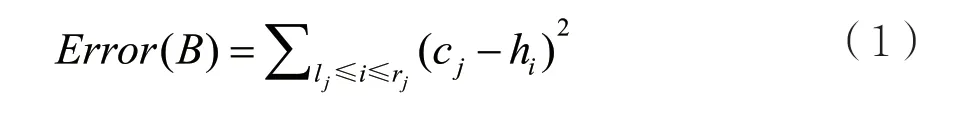
所以可以給出Error(H*,H)的計算公式：

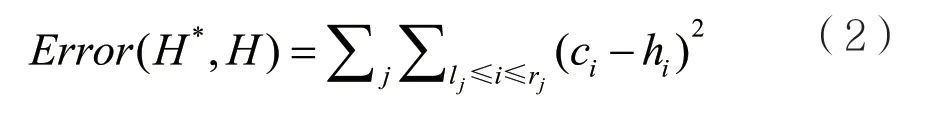
貪心策略是降低桶劃分誤差的一種有效方法，所以在桶合并過程中將使用貪心策略。劃分過程中，如果兩個相鄰的桶誤差最小，則將這兩個桶作為合并的對象。

定義8 相鄰桶的距離：將相鄰兩個桶進行合并必然存在一定誤差，而誤差會出現累計作用，將這種作用稱為誤差增益，即相鄰桶的距離，表示為dis(Bj,Bj+1)，計算公式如下：

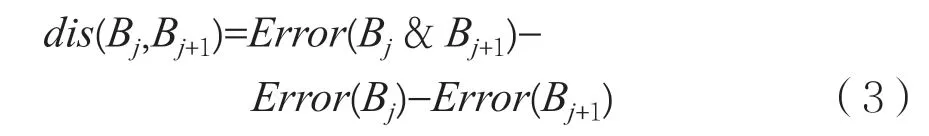
將兩個相鄰且欲合并的桶分別記為Bj與Bj+1，則合并后的新桶記為Bj& Bj+1。兩個桶分別產生的誤差分別記為Error(Bj)和Error(Bj+1)，而兩個桶合并之后的誤差記為Error(Bj& Bj+1)。

數據的失真程度會因桶劃分策略的不同而不同。相關文獻中對桶劃分策略進行了設計[9]，但是由于算法采用動態規劃策略尋找最優的桶劃分方案，算法執行效率不高。如何設計有效的桶劃分策略且不使數據失真，是本文研究的重點。

本文首先考慮將原始直方圖H的m個數據放進m個桶，此時m和k相等。其次，對兩個相鄰的桶進行合并，采用的策略是貪心策略。眾多桶被合并后，桶的數量逐漸減少，最終形成m個不同的合并桶，相應的需要使用m個不同的劃分策略，將這些劃分策略分別記為Hm,Hm-1,…,H2,H1,。由于優劣程度不同，因此總會存在一個最優策略。為此需要從中選擇一個最優的劃分策略，并對其他策略的優劣進行評價。采用文獻[9]中的方法進行評價，即：

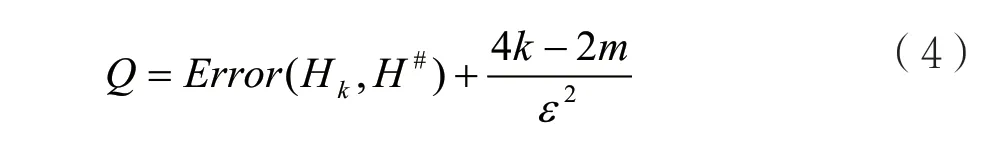
桶劃分策略越好，對應的Q值越小。實際選取時，桶可能不是最相鄰的。因此，為了保證兩個桶是相鄰的，需要對兩個桶的距離進行計算，將兩個桶分別記為Bj與Bj+1，則距離表達式為dis(Bj,Bj+1)，具體操作方法如下。

算法2：桶劃分貪心算法（Greedy Algorithm）

輸入：原始直方圖H，差分隱私參數ε

輸出：經過優化處理后的帶噪聲計數序列H#作為輸出。

步驟：

（1）設k為桶的數量，初始化時k=m，把H的m個數據序列元素分別放入k個桶中；

（2）對兩個桶的距離dis(Bj,Bj+1)進行計算，采用貪心算法，最終將兩個最相鄰的桶進行合并處理，從而使總桶的數量減少1個；

（3）重復操作上述步驟（2），如果滿足k=1，則停止，同時將Q最小的取值記為k*；

（4）求得桶內所有元素的平均值，并將該值賦予給桶內每個元素，然后將m個新值賦予到M′，并對該值進行輸出；

（5）向新生成的直方圖M′的每一頻數添加獨立拉普拉斯噪聲Lap(1/ε)，得到矩陣H#；

算法2的時間復雜度涉及到下面幾個方面：原始數據表T首先需要轉換為初始直方圖H，該過程需要消耗一定的時間，將相應的時間復雜度記為O(n)；將拉普拉斯噪聲加入到序列M中，可以得到序列H#，該過程也需要消耗一定的時間，將相應的時間復雜度記為O(m)；采用多種不同的桶劃分策略，這里將其數量記為m，在具體尋找兩個相鄰的桶時，需要使用枚舉法，從而對兩個桶機進行合并處理，該過程需要消耗一定的時間，相應的時間復雜度記為O(m2)。因此，可以將上述時間復雜度進行綜合，從而可以得到算法2的時間復雜度表達式應是O(n+m2)。

3.2.3 保序回歸算法（Isotonic Regression）

在重構序列中添加噪聲進行擾動達到隱私保護的需求，但這個過程不僅對每一個序列值造成了一定的信息丟失，而且破壞了序列的排序約束[12]。如果在噪聲擾動后的序列上按照原始序列的排序約束進行校正，不會對直方圖的隱私特性有任何破壞，反而可以提高直方圖序列的精確度，從而提高直方圖的查詢精度。依照排序約束進行序列校正的過程是采用保序回歸算法實現的。

保序回歸[13]（Isotonic Regression）是數值分析中經常用到的一個方法，使用一個最小的數據校正量來保證數據的有序性。將保序回歸算法運用到基于差分隱私的直方圖發布中，這里設一個任意序列為S，欲得到的有序序列為s′。兩個序列滿足||ss′||最小。當1≤i≤n時，s′[i]和s′[i+1]滿足關系s′[i]≤s′[i+1]。下面介紹序列s′的確定過程。首先對序列s的第一個元素進行校驗操作，遇到無序子序列時，求該子序列的平均值，進而用平均值進行替換，然后將其和后一個數值進行比較，判斷是否有序。重復上述步驟，直到完成所有數據的檢驗。該操作過程可以用算法表示，具體如下。

算法3：基于差分隱私的保序回歸算法

算法輸入與輸出：原始序列S、有序序列s′

步驟：

（1）記錄下序列S的原始序列和S的升序形式R；

（2）對原始序列S進行加噪得到加噪后的序列S*；

（3）記錄序列S*的升序形式R*；

（4）查看R*中失序的數值，將所有失序的數值去掉，以其平均值取代每一個失序的數值，生成新的序列R**；

（5）對R**中的數值按照S的初始序列恢復，生成有序序列s′，算法結束。

下面舉例說明差分隱私直方圖發布中保序回歸算法的實現，計算中數據保留兩位小數。

（1）假設加噪聲前的原始序列S為{3,2,2,5,4,1,2}；

（2）對S的值按照升序排列則變為{1,2,2,2,3,4,5}；

（3）加噪后的原始序列變為{3.12,2.03,1.98,5.25,4.17,2.53,2.21}；

（4）對加噪后的序列再按升序排列，結果為{2.53,2.03,1.98,2.21,3.12,4.17,5.25}。顯然，加噪后由于噪聲大小存在一定的隨機性，S中最小的數1變成了2.53，超過了S中比1大的三個數2.03、1.98和2.21。

（5）根據保序回歸算法3，以其平均值2.19取代亂序的四個頻數2.53、2.03、1.98和2.21。

（6）那么加噪后由小到大的序列變為{2.19,2.19,2.19,2.19,3.12,4.17,5.25}，恢復了正常序列。

（7）對步驟（6）中產生的序列按照初始序列S的順序進行恢復，得到算法的最終序列s′={3.12, 2.19,2.19,5.25,4.17,2.19,2.19}。

序列s′的排序約束是全部過程實現的基礎。為了保證噪聲干擾后的分量和干擾前的排序相同，需要引入最小校正分量。采用上述方法可以獲得噪聲誤差 E rror ( D,)=2.186 4，該誤差是沒有使用保序算法的誤差，而經過保序算法處理后的噪聲誤差記為Error(D,Hs)，相應的值為1.293 2。因此，和沒有經過處理的相比，降低明顯。誤差降低的幅度和付出的代價相比是合理的。對于實際的應用，保序回歸算法更具有價值。

4 實驗結果與分析

基于本課題為上海市科委“科技創新行動計劃”項目——基于大數據的慢病管理平臺數據安全和隱私保護的子課題，因此實驗數據源選用項目合作方上海萬達信息有限公司的慢病數據庫中的病歷數據。

為了使數據具有代表性，采用的實驗數據采用3種不同的數據集。數據集Age是慢病數據庫中的年齡屬性的統計集，記錄數量為10 247 691，分為103個桶，分別對應103個年齡；數據集Location是數據庫中慢病病人的戶籍所在地的統計集，共186 461個記錄，精確到村或者街道，分為3 829個桶，對應3 829個鎮或者街道；數據集Social network為數據庫中糖尿病病人相互之間的親友關系的統計集，共81 793條記錄，對應18 639個桶，也就是18 639個病人，如表1所示。

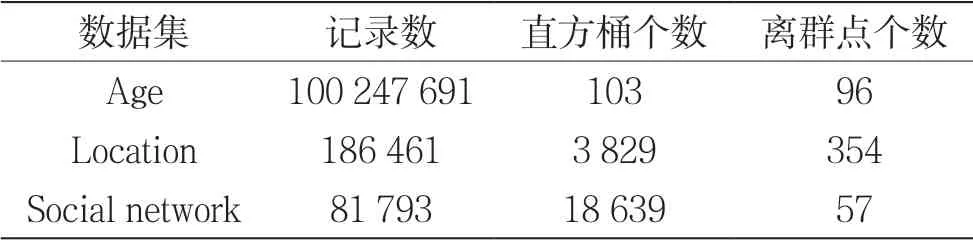
表1 數據集規模

實驗的硬件環境為Intel（R）Core（TM）i7 CPU，8 GB內存，操作系統平臺為Windows 7操作系統，采用Python語言實現所有方法。

為了說明本文提出的R-G-I方法能夠在差分隱私保護下保證發布攜帶離群點直方圖數據的準確性，本實驗將R-G-I方法分別與NoiseFirst、StructureFirst、P.HPartition三種方法進行比較（以下分別簡稱RGI、NF、SF、PHP方法）。采用MSE（MSE為查詢指定范圍內各種算法輸出的直方圖與原直方圖各個桶頻數的查詢誤差平方和的均值）指標來衡量在不同查詢范圍內數據發布的準確性。為了使實驗更具說服力，每種算法均運行20次，取總次數實驗結果的均值作為該算法的最終結果。因此，在同樣的隱私保護級別下，本實驗更關注數據發布結果的準確性。

4.1 驗證R-G-I方法中降低交替分布度算法（Reduce ADD）的有效性

針對含有離群點的原始直方圖，為了消除離群點產生較大的交替分布度對直方圖重構的影響，本文給出了梯度回歸算法。本組實驗主要用梯度回歸算法分別將傳統的直方圖發布算法（NF、SF、PHP）輸入的原始直方圖進行預處理，并且通過對比預處理和未預處理后的實驗結果，驗證梯度回歸算法的有效性。實驗結果如圖1～圖3所示。

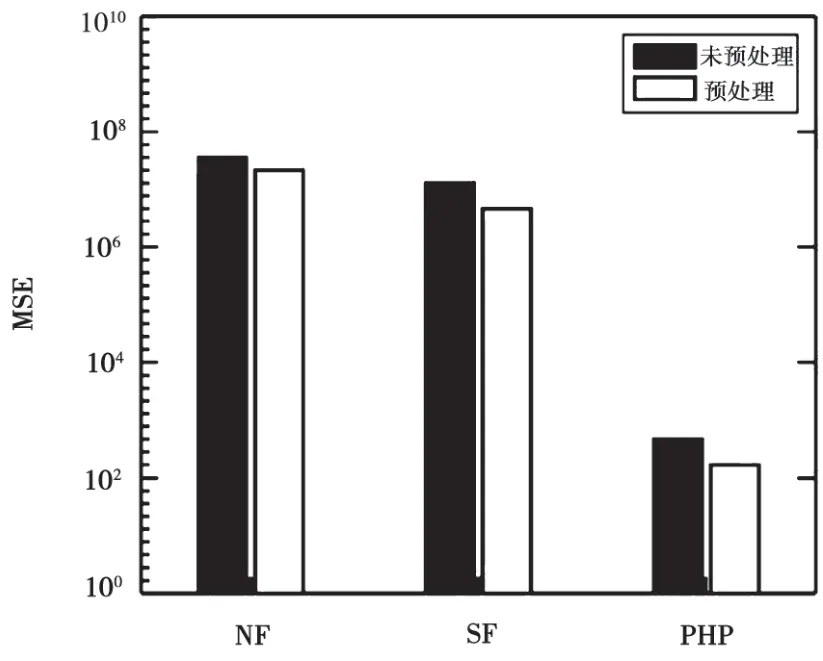
圖1 Location數據集上對比實驗結果（ε=0.01）

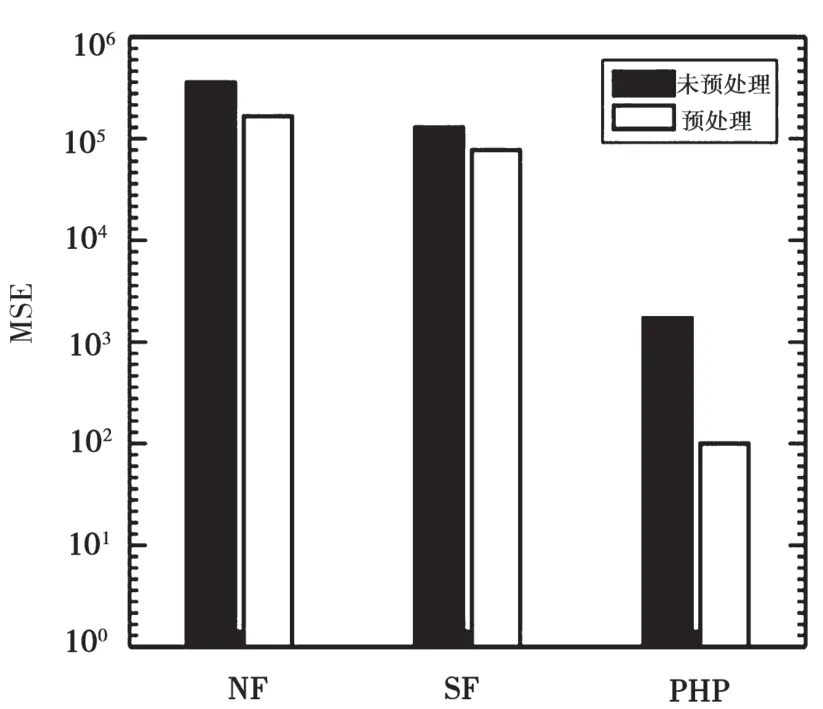
圖2 Location數據集上對比實驗結果（ε=0.1）

可以看到，深色柱代表直接采用現存的直方圖發布算法作用在Location數據集上的MSE誤差值，空柱代表將Location數據集先采用Reduce ADD算法進行預處理后，再采用NF、SF、PHP三種方法的MSE誤差值。由于隱私預算ε越大，說明隱私批漏風險越大，隱私保護程度越小，則數據發布準確性越高，因此可以發現參數ε越大，所有方法的MSE誤差值越小。然而，無論參數ε（O.01、0.1、1）取何值，對數據集進行預處理的MSE值都要小于未進行預處理的MSE值。因此，本實驗驗證了梯度回歸算法通過降低交替分布度最大程度地降低了離群點對直方圖重構的影響。

4.2 驗證四種方法作用在四類不同的數據集上的MSE值的差異

MSE越小，表示數據發布的準確性越高。每種方法設置隱私預算參數分別為0.01、O.1、1。設計數據集Location、Social Network的查詢范圍為100～500，Age的查詢范圍為0～100且間隔相同的查詢函數。

本組實驗中，主要檢驗各個方法在不同查詢范圍下的查詢結果，該組實驗中采用MSE衡量數據發布的準確性。圖4～圖6給出了不同隱私預算下作用在四種數據集的MSE結果。其中，橫坐標代表三種數據集，縱坐標代表誤差值。ε越大，表明隱私保護水平越低，數據發布的準確性越高，MSE值也相對越小。實驗結果可知，R-G-I方法的MSE值較其他三種方法明顯要小，顯著地提高了數據發布精度。

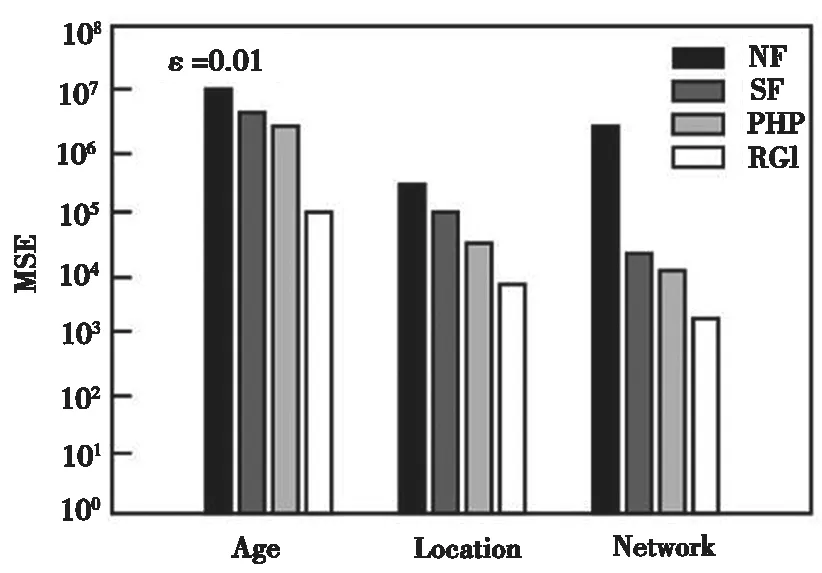
圖4 四種方法的MSE值比較（ε=0.01）

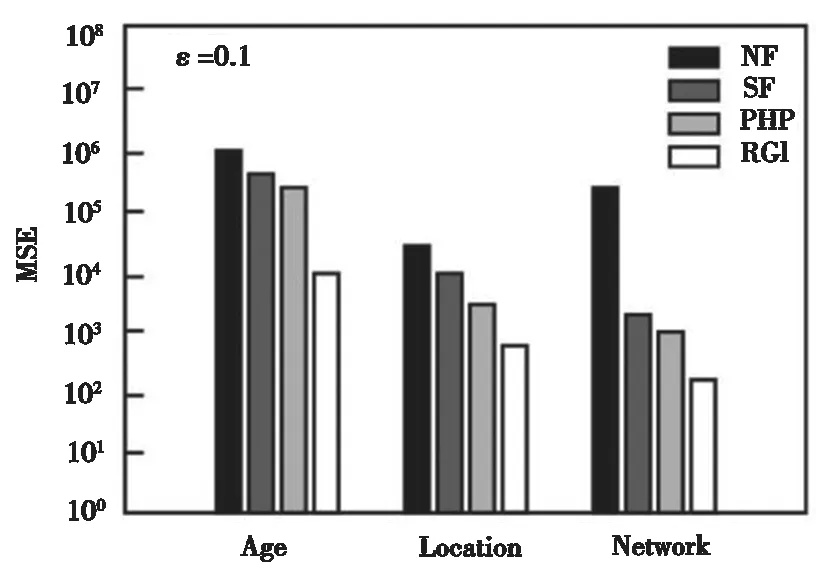
圖5 四種方法的MSE值比較（ε=0.1）

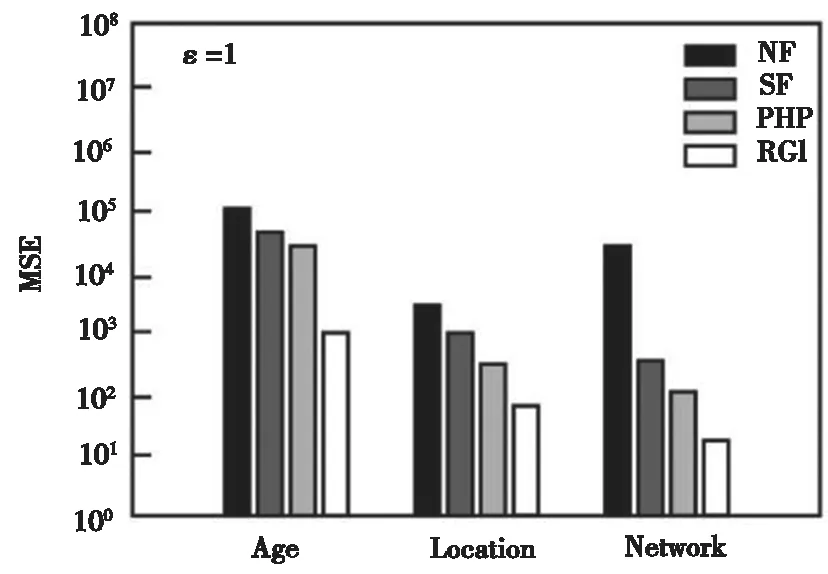
圖6 四種方法的MSE值比較（ε=1）

5 結 語

本文針對存在離群點的差分隱私直方圖發布，提出了一種基于桶劃分的R-G-I方法。該方法包括三個重要的算法——梯度回歸算法、基于桶重構的貪心算法和保序回歸算法。其中，梯度回歸算法主要是對原始直方圖進行滿足差分隱私的排序，從而減小交替分布度；貪心算法主要采用指數機制每次選擇直方圖中最相似的兩個鄰近桶進行合并，最后通過加入拉普拉斯噪聲對重構后的新桶頻數進行擾動；保序回歸算法在噪聲擾動后的序列上，按照原始序列的排序約束進行校正，提高了直方圖序列的精確度，從而提高了直方圖的查詢精度。最后，采用不同特點的真實數據集進行實驗，實驗結果驗證了提出的R-G-I方法針對含有離群點的數據集的準確性和有效性。