基于雙樹復小波變換與引導濾波的紅外與可見光圖像融合算法*

齊海生，榮傳振，肖力銘，岳振軍

（陸軍工程大學，江蘇 南京210007）

0 引 言

圖像融合是將多傳感器采集的同一場景的圖像進行融合，取得信息互補的過程。其中，紅外與可見光的融合近年來受到廣泛關注，在軍事領域起到了非常重要的作用[1]。紅外圖像成像主要是利用紅外熱像儀成像獲得低光照條件下或者有障礙遮擋的物體的圖像，具有良好的探測性能，但紅外成像對比度低、紋理細節信息缺失。可見光圖像由可見光傳感器成像，具有較高的對比度和豐富的紋理細節信息，有利于人眼對場景的認知，但在光照較差或有障礙物遮擋等條件下所成圖像效果較差。把紅外圖像與可見光圖像進行有效融合，既能突出紅外目標信息，又可以得到可見光圖像的高分辨率細節信息，因此被廣泛應用于計算機視覺、航天學及軍事等領域。

近年來，基于變換域的圖像融合方法成為研究熱點，尋找適合紅外與可見光圖像融合的多尺度分解與重構方法成為一個重要的研究方向。小波變換因其多分辨特性能夠捕捉信息的奇異點，成為最常見的變換域工具。但是，小波變換方向選擇性少，會導致目標邊緣不清晰，因此出現了各類改良小波，如脊波變換[2]、曲波變換[3]以及輪廓波變換[4]等。這些改進改善了圖像融合效果，但都存在缺憾，如有的不能檢測曲線奇異，有的冗余度高、計算復雜，有的不具有平移不變性，融合圖像存在振鈴現象。近年，在小波變換的基礎上發展的雙樹復小波變換[5]，不僅保留了小波的時頻分析特性，還具有近似的平移不變性、多方向選擇性（6個方向）以及有限的數據冗余，且計算效率較高，重構效率好，成為當前應用比較廣泛的工具。

在紅外與可見光圖像融合中，還需要充分考慮提取圖像顯著信息的空間一致性，否則融合圖像會出現光影或者重影現象。Li[6]等人提出了一種基于引導濾波的圖像融合方法，有效解決了空間一致性問題，但仍存在問題：（1）生成的顯著圖不能很好地表示圖像中的視覺顯著特征；（2）圖像分解方向單一，不能全方位體現圖像各方向的特征。

為此，本文提出了一種基于雙樹復小波變換和引導濾波器的紅外與可見光圖像融合算法，對源圖像進行分解后，低頻子帶采用一種改進的基于圖像區域能量和的融合規則進行融合，高頻子帶則結合引導濾波特性，設計基于改進的區域能量和的融合規則，并通過實驗驗證了算法的優越性。

1 相關理論

1.1 雙樹復小波變換原理

kingsbury提出的雙樹復小波變換（DTCWT），相比于離散小波變換，具有優秀的方向選擇性、良好的平移不變性、有限的數據冗余、高效的計算效率以及優良的重構效果等優點，從而被廣泛應用于各種圖像處理工作[7]。DTCWT使用兩個單獨的離散小波樹，其中一路的小波變換作為實部，另一路小波變換作為虛部。兩個分解樹（樹A和樹B）平行，假如樹A給出實部，樹B則定義為虛部。圖1為DTCWT的分解示意圖。

圖1 雙樹復小波變換

兩棵樹分別作用于圖像的行上和列上，產生雙樹結構。每一級分解時得到兩個低頻近似子帶分別記作A(j+1,1)和A(j+1,2),同時得到6個不同方向（±15°，±45°，±75°）的高頻子帶D(j+1,m)，m=1，…，6。該方法比離散小波變換多了3個方向，可提高圖像分解與重構的精度，并能夠保留圖像的細節信息。無論二維雙樹復小波變換分解層數是多少，總體冗余都是4∶1.

1.2 引導濾波

圖像引導濾波器[8]是一種局部線性濾波器。與傳統的濾波器相比，圖像引導濾波器在保持圖像邊緣梯度的同時，能夠增強圖像的細節信息，保留輸入圖像的整體特征，被廣泛應用于圖像去噪、圖像傳輸和圖像融合。

假設引導濾波器的引導圖像為I，輸入圖像為p，輸出圖像為q，則在以k為中心、r為半徑的窗口Wk中，輸出圖像與引導圖像存在以下線性關系：

式中ak、bk為窗口的線性系數，均為常數，i、k為像素點坐標。從式（1）可以看出， Iaq ?=? ，保證了輸出圖像q與引導圖像I的邊緣一致性。下一步是求出線性函數的系數，也就是線性回歸，即希望擬合函數的輸出值與真實值p之間的差距最小，即式（2）最小：

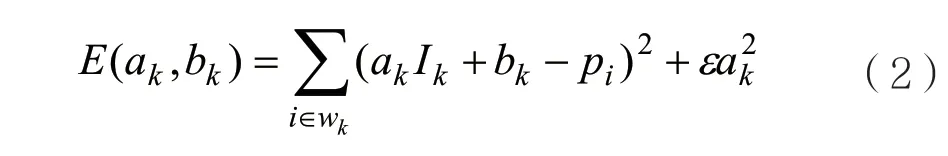
式中ε是為了防止系數過大而定義的正則化參數。利用最小二乘法對求解式（2），可得出ak、bk的最優解：

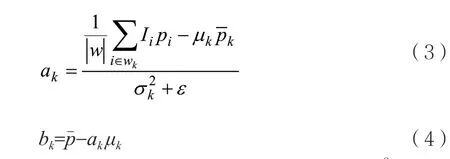
uk是引導圖像I在窗口中的平均值，σ2k是I在窗口wk中的方差，|w|是窗口wk中像素的數量，p-k是待濾波圖像p在窗口wk中的像素均值。對于整幅圖像，計算出每個包含像素點i的窗口內的qi值，得到最終的濾波輸出圖像為：

2 融合規則

2.1 基于改進的區域拉普拉斯能量和的低頻融合規則

多尺度變換域的低頻系數中包含圖像的大部分信息和能量，因此低頻系數融合規則的選取非常重要。拉普拉斯能量和（SML）[9-10]反映了圖像的邊緣特征信息，一定程度上能恰當反映圖像的客觀情況，但還存在問題：只在水平和垂直方向上計算每個像素點的變步長拉普拉斯能量值，未考慮對角方向。為此，本文采用一種改進的拉普拉斯能量和選取方法，并據此選擇圖像的低頻系數，以獲得更好的圖像融合效果。

其中，改進的區域拉普拉斯能量和定義為：

其中：

式中w(a,b)為權值矩陣，定義為：

從而，根據該改進方法的低頻融合規則：

其中，I1(i, j)、I2(i, j)分別為兩幅圖像的低頻分解系數，ENS1(i,j)、ENS2(i,j)分別為兩幅圖像改進的拉普拉斯能量和，F(i, j)為低頻融合系數。

2.2 基于引導濾波的高頻系數融合規則

人類視覺系統對邊緣、方向以及紋理等比較敏感，基于區域能量的規則可以滿足這一要求。因此，本文采用同低頻系數相同的方法得到高頻系數的加權矩陣。但是，圖像中的噪聲主要集中在高頻部分。為了有效抑制噪聲對融合效果的影響，本文應用引導濾波優化高頻系數加權矩陣，使得亮度相近的相鄰像素值也具有相近的權重，從而滿足空間一致性。

首先利用式（6）求取高頻系數區域能量，再利用絕對值取大原則得到高頻系數加權映射矩陣，最后通過式（14）優化高頻系數加權矩陣。

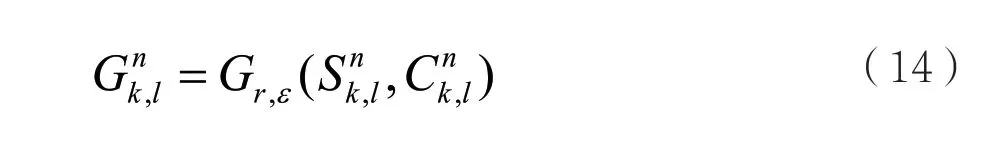
r為窗口半徑；Snk,l為第n幅圖像的k尺度l方向的加權映射矩陣，作為引導濾波的輸入；Cnk,l為第n幅圖像的k尺度l方向的系數矩陣，作為引導濾波的引導圖；Gr,ε為引導濾波函數。

從而，高頻系數的重構可表示為：

3 融合步驟的設定

本文融合采用如下規則：

（1）利用雙樹復小波變換將源圖像分解為低頻系數和高頻系數；

（2）采用改進的基于區域拉普拉斯能量和取大的融合規則進行低頻系數融合；

（3）采用基于區域拉普拉斯能量和取大與引導濾波的方法對高頻系數進行融合；

（4）將步驟（2）和步驟（3）中融合后的低頻和高頻系數，通過逆雙樹復小波變換重構得到融合圖像。

具體過程如圖2所示。

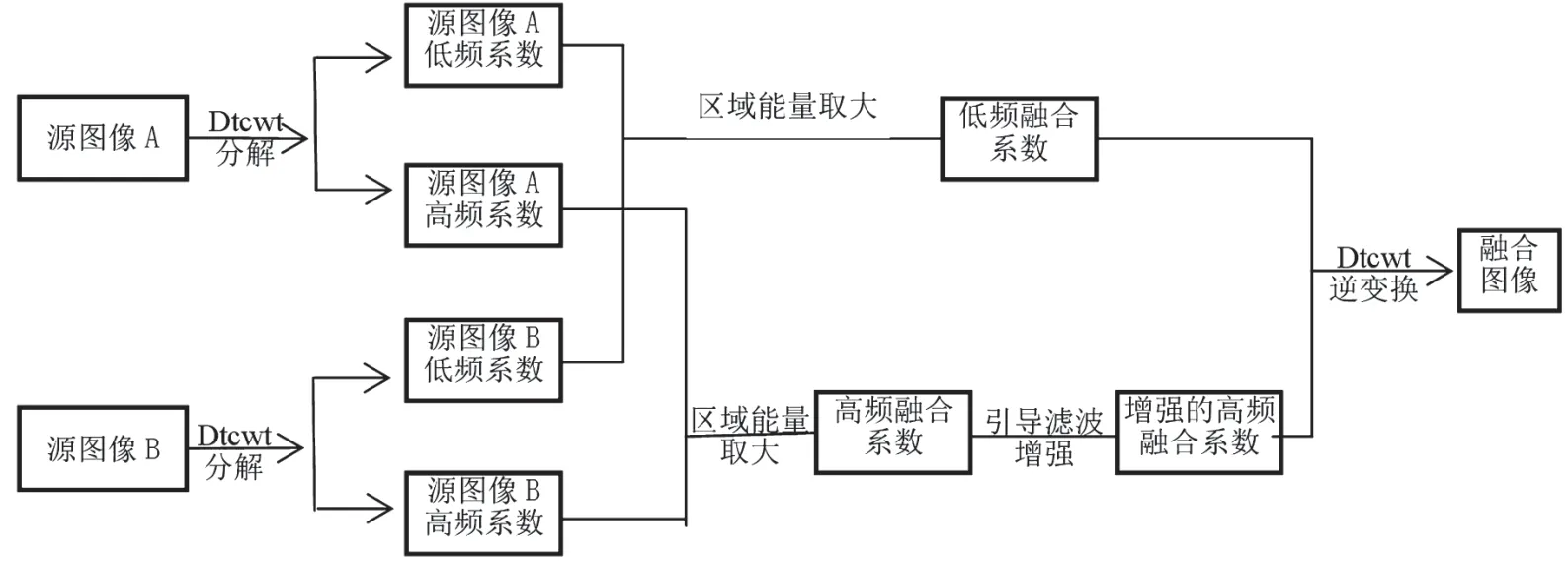
圖2 基于DTCWT與引導濾波的圖像融合流程

4 實驗結果與分析

為檢驗算法特性，對雙樹復小波變換分解層數進行實驗驗證，其中低頻系數和高頻系數均采用本文的方法進行融合，以取得更優的參數，結果如圖3、表1所示。由實驗結果可知，最優分解層 數為4。

圖3 融合圖像一

表1 不同分解層數的融合結果對比

在同一種融合策略下，采用不同的變換域對源圖像進行分解，通過對融合結果進行比較，說明本文方法的優越性。在不同的變換域下采用不同的融合策略，可以說明本文算法優于其他算法。這部分主要針對紅外與可見光圖像進行實驗比較。具體地，在傳統的融合策略（低頻取平均值，高頻絕對值取大）下選用拉普拉斯金字塔變換（LP）[11]、離散小波變換（DWT）[12]、curvelet變換[13]以及本文方法進行結果比對。為了評價融合結果，采用的客觀評價指標有信息熵、互信息量和邊緣相似度。

為了使結果更具說服力，對3組紅外與可見光圖像進行仿真實驗，源圖像及融合結果如圖4～圖6 所示。其中，每幅圖像中的前兩個均為源圖像，其余為采用上述算法獲得的融合結果。

圖5 融合圖像三

圖6 融合圖像四

從3組融合圖像來看，4種融合方法均提取到了源圖像的互補信息，融合后圖像能反映兩幅源圖像所表達的內容；融合圖像中，（c）、（d）圖像有明顯的塊效應，圖像整體較為模糊，圖像（e）中出現了一些鋸齒狀紋理，圖像（f）的融合效果大大改善，圖像自然明亮，對比度適中，區域特征比較明顯。

從客觀的信息熵[14]、互信息量[15]以及邊緣相似度[16]三方面對融合結果進行定量分析，結果如表2所示。

表2 不同算法融合結果對比

從客觀評價指標看，本文方法優于傳統融合規則下的其他變換域融合方法，能有效保留圖像的邊緣和輪廓信息，驗證了本文算法的有效性。

5 結 語

本文采用基于雙樹復小波變換與引導濾波的方法對紅外和可見光圖像進行融合，在融合規則的設定上，圖像分解完成后，對低頻部分進行基于引導濾波的方法進行融合，高頻部分進行基于改進的區域能量和的方法進行融合，并與傳統的多尺度分解融合方法進行比較分析。結果表明，本文提出的方法能有效保留源圖像的輪廓和邊緣信息，主觀視覺上融合圖像自然清晰，對比度適中，客觀評價指標上也優于其他方法。