基于指數函數的變步長仿射投影符號算法

李雪蕊，林 云

（重慶郵電大學通信與信息工程學院，重慶 400065）

0 引 言

隨著通信技術和信號處理的飛速發展，自適應濾波器在工程實踐中的應用愈加廣泛，如信道均衡、回聲消除和系統辨識等。在自適應濾波算法中，常見的有最小均方算法（Least Mean Square， LMS）和最小二乘算法（Recursive Least Square，RLS）。其中，LMS算法的優點是計算復雜度低，缺點是當輸入信號自相關矩陣的特征值分布范圍廣時，算法收斂速度緩慢。RLS算法的優點是收斂速度快，缺點是穩定性差，計算復雜度高[1]。為了改善LMS算法和RLS算法存在的缺陷，文獻[2]首次提出了仿射投影算法（Affine Projection Algorithm，APA）。APA通過重復利用過去的輸入信號改善算法的相關性能，計算復雜度和收斂速度均介于LMS與RLS算法之間[3]。但是，當系統存在沖激噪聲時，APA算法將會受到嚴重干擾，無法表現出良好的跟蹤性能。為了解決這一問題，文獻[4]將APA算法與符號算法（Sign Algorithm，SA）相結合，提出了一種能夠抗沖激干擾的仿射投影符號算法（Affine Projection Sign Algorithm，APSA）。然而，傳統的固定步長參數的APSA算法無法平衡收斂速度與穩態誤差之間的矛盾，于是變步長仿射投影符號算法（Variable Step Size Affine Projection Sign Algorithm，VSS-APSA）得到了很大發展。變步長技術通過令算法在初始階段具有較大的步長值保證算法的快速收斂，同時在算法接近穩態階段具有較小的步長值，保證了算法具有小的穩態誤差[5-7]。因此，變步長技術可以很好地調節收斂速度和穩態誤差之間的矛盾。文獻[8]首次提出了VSS-APSA，但是其采用最小化函數更新步長，不能實時跟蹤系統的變化，且在非穩定環境下性能嚴重衰減。文獻[9-10]則分別提出了改進后的算法。

本文在基于修改后的誤差函數基礎上，提出了一種利用無噪先驗誤差的功率與步長的非線性關系對步長值進行迭代更新的新的VSS-APSA算法。仿真結果表明，該算法與傳統APSA算法、VSSAPSA算法相比，具有更快的收斂速度、更低的穩態誤差和更高的穩定性。

1 傳統的APSA算法

圖1給出了系統辨識模型下的自適應濾波器框圖。濾波器的長度為L，第n次迭代的輸入為un=(un,un-1,…,un-L+1)T，ωn為濾波器第n次迭代時對ωo的估計值。期望信號dn=uTnωo+vn，誤差信號en=dn-uTnωn-1。

APA算法雖然在輸入信號嚴重相關時仍具有很快的收斂速度，但是當系統存在沖激噪聲時，性能會嚴重衰減。為此，人們將基于l1范數的SA算法與APA算法相結合，提出了能夠抗沖激干擾的APSA算法。APSA算法的濾波器系數更新公式的推導過程如下：

利用拉格朗日乘數法，將式（1）改寫為：

對式（2）兩邊關于ωn求導，并令其等于零，得：

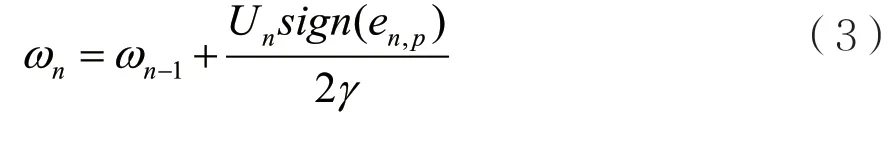
由式（1）、式（2）和式（3），可得APSA算法的濾波器系數更新公式：

式中，en,p代表后驗誤差矢量，μ代表步長參數，γ代表拉格朗日乘子，Un代表輸入信號矩陣，sign(·)代表符號函數，en代表先驗誤差矢量，T代表矩陣的轉置。式（4）中，由于無法在實踐中獲得en,p，因而用en來近似en,p。

2 VSS-APSA算法

2.1 傳統的VSS-APSA算法

固定步長的APSA算法，主要缺點是無法調節收斂速度和穩態誤差之間的矛盾。因此，變步長技術是一個能夠解決這一問題的好方法。文獻[8]中提出的VSS-APSA基于最小均方偏差（Mean Square Deviation，MSD）準則，推導過程如下：

其中， ω ～n=ωo-ωn，μn代表可變步長。

對式（5）兩邊取l2范數平方的期望，得：

對式（6）關于μn求導，并令其為零，得：

傳統的VSS-APSA算法雖然改善了APSA算法的收斂性能和穩態誤差性能，但是由于去掉了噪聲項，因此計算的步長值并不是最優的，且在變步長μn的更新公式中由于應用了最小函數，因此該算法在非穩定環境下的性能將會嚴重衰減。

2.2 新提出的VSS-APSA算法

標準的誤差函數公式為：

本文所用到的修改后的誤差函數為：

圖2給出了標準誤差函數和修改后誤差函數的函數圖象。

圖2 不同的誤差函數圖像

由圖2可以看出，修改后的誤差函數具有非負性和對稱性，且當x=0時取得最小值0，當x趨于無窮大時能夠比標準誤差函數更快地收斂于最大值1。這些特性意味著如果采用修改后的誤差函數更新步長，在初始階段，函數的變化速率較快，即算法的收斂速度快；在穩態階段，函數的變化速率趨于零，即算法的穩態誤差低；當出現沖激干擾時，函數值為1，即步長不再進行更新，從而保證了算法具有良好的抗沖激噪聲特性。

本節提出一種基于修改后的誤差函數的VSSAPSA算法。通過使用修改后的誤差函數作為步長函數，新算法利用無噪先驗誤差的功率與步長的非線性關系對步長值進行迭代更新，迭代公式為：

式中，ρ＞0代表比例參數，en,f=en-vn=(ωo-ωn)Tun代表無噪先驗誤差，E(e2n,f)=E(e2n)-E(v2n)代表無噪先驗誤差的功率。由于E(e2n,f)在計算過程中需要用到輸入信號的統計信息，因此無法直接通過計算得出所需的期望值。針對這一問題，文獻[11-12]給出了一種遞歸方法對期望值進行估計：

式中，ε代表極小的正數，作用是避免輸入信號的功率為零時算法停滯；E(e2n)代表誤差信號en的功率，E(v2n)代表環境噪聲vn的功率，E(u2n)代表輸入信號un的功率，Rn,eu代表輸入信號與誤差信號的互相關矩陣。

實際應用中，由于無法獲得輸入信號的功率以及輸入信號與誤差信號的互相關矩陣，因此 文獻[11-12]提供了一種遞歸方法用于對其進行近似計算：

式中，β代表平滑因子。

綜上，本節提出一種新的VSS-APSA算法，它的濾波器系數更新公式為：

式中步長μn由式（11）控制。

3 算法仿真與性能分析

仿真采用一個脈沖響應長度為L=32的待辨識系統。輸入信號是均值為零的高斯白噪聲，輸出信噪比為30 dB，沖激噪聲由kiAi產生，ki是成功概率P[ki=1]=pr的伯努利過程，本次試驗設定pr=0.05。Ai是均值為零的高斯隨機過程，且其功率為σ2A=1 000σ2y，σ2y是自適應系統的輸出功率。本次試驗采用歸一化均方偏差（Normalized Mean Square Deviation，NMSD）作為衡量算法性能的標準，其中其中ω ～i=ωo-ωi。所有的仿真結果都是通過對100次獨立實驗結果取平均而獲得。

圖3給出了在沒有沖激噪聲干擾的情況下，當投影階數K=2、μ1=0.01、μ2=0.000 5、ε=0.000 1時，新算法與APSA[4]的NMSD隨迭代次數變化的性能曲線圖。由圖3可見，與傳統的APSA算法相比，新算法表現出更快的收斂速度和更低的穩態誤差，且當ρ=0.05、β=0.995時，新算法可取得最優性能。

圖3 不同參數下新算法的性能曲線

圖4給出了當沖激噪聲干擾存在時，不同投影階數下傳統APSA、VSS-APSA[8]與新算法的性能曲線圖。其中，在傳統APSA算法中，K=4。雖然VSS-APSA算法在前5 000次迭代性能優于新算法，但其跟蹤性能在沖激噪聲出現后嚴重衰減。這種衰減是由式（8）中的最小函數導致的。然而，新算法在沖激噪聲出現前后均表現出良好的跟蹤性能，即新算法的抗沖激噪聲性能優于傳統的APSA和VSS-APSA。

圖4 不同投影階數下各算法的性能曲線圖

4 結 語

本文在基于誤差函數的基礎上，提出了一種新的變步長仿射投影符號算法。通過使用修改后的誤差函數作為步長函數，提出的算法利用無噪先驗誤差的功率與步長的非線性關系對步長值進行迭代更新，并與APSA、傳統VSS-APSA算法進行了比較。仿真結果表明，與傳統變步長仿射投影符號算法相比，提出的算法具有更快的收斂速度、更小的穩態誤差以及更強的抗沖激干擾特性。