*不確定條件下提高靜態電壓穩定性的優化方法

邱一葦，林 今，吳 浩，宋永華，

(1.清華大學 電機工程與應用電子技術系，北京 100084；2.浙江大學 電氣工程學院，杭州 310027；3.澳門大學 電子與計算機工程系，澳門 999078)

在當前電網大尺度跨區域互聯，風、光等可再生能源發電跨越式發展，電力市場化改革不斷深化的背景下，電力系統運行中的不確定性因素日益增多，其電壓穩定性正受到全方位的考驗[1-3]。為確保運行安全，有必要對電力系統在不確定性條件下的靜態電壓穩定性進行優化。

在不確定條件下的靜態電壓穩定性評估上，學界和業界已積累了許多積極的研究成果[4-10]。其中，靜態安全域類評估方法通過離線計算獲得參數空間中安全域邊界的顯式表示，在線運行時通過對比當前運行點與域邊界的位置關系快速評估系統的靜態電壓穩定性，極大地提高了評估效率和靈活性[7-10]。但直接利用概率評估結果，提高不確定條件下電力系統靜態電壓穩定性的優化研究尚為有限。

為此，本文基于靜態安全域思想提出了一種不確定條件下提高電力系統靜態電壓穩定性的優化方法：以最大化隨機變量位于靜態電壓穩定域內的概率為目標，利用靜態電壓穩定域邊界及控制變量對其靈敏度的顯式逼近表達式構造優化模型；為此，引入廣義多項式混沌(generalized polynomial chaos,gPC)思想，結合隨機Galerkin方法和經典原-對偶內點法，求取靜態電壓穩定域邊界及其靈敏度的顯式多項式逼近表達式；最后，通過IEEE-39節點系統算例驗證了所提方法的有效性和精確性。本文建模與計算工作在浙江大學智能電網運行與優化實驗室開發的MASTES電力系統分析和仿真工具包[11]上進行。

1 不確定條件下的靜態電壓穩定優化模型

1.1 基于靜態電壓穩定域的優化模型

本文所提優化模型的目標在于，當電力系統中的隨機變量服從一定隨機分布時，通過調整運行點使系統靜態電壓失穩的概率最小化。

記多維獨立隨機變量構成向量：

Z=[Z1,Z2,…,Zn]∈Qn?Rn.

(1)

式中：Zi∈Qi為第i個獨立隨機變量；Qi為第i個獨立隨機變量的支持域；Qn=Q1?Q2?…?Qn為隨機向量的支持域。對于含有非獨立隨機變量的情形，需進行預處理使之相互解耦，參見1.3節。

為刻畫系統靜態電壓失穩的概率，引入靜態電壓穩定域[7]概念。計及發電機無功出力約束時，電力系統的穩態模型[13]如下所示：

0=f(V,θ,Ps,QG;λ,Z) .

(2)

(3)

(4)

(5)

基于上述模型，定義概率空間中的靜態電壓穩定域，如下：

ΩSVSR={Z∈Qn?Rn|系統(2)-
(5)運行點存在} .

(6)

顯然，當隨機變量位于域內時，系統靜態電壓穩定；反之意味著失穩。因此，系統靜態電壓穩定的概率即隨機變量位于靜態電壓穩定域中的概率：

(7)

式中：dW(Z)=dW1(Z1)dW2(Z2)…dWn(Zn)為多維概率空間的測度；dWi(Zi)=ωi(Zi)dZi為第i個獨立隨機變量所在概率空間的測度；ωi(Zi)為第i個獨立隨機變量的概率密度函數；且

(8)

至此，以最大化多維隨機變量處于靜態電壓穩定域內的概率為主要目標，兼顧控制變量的調整幅度，定義不確定條件下提高靜態電壓穩定性的優化模型，如下：

min-ΔP(Z∈ΩSVSR)+(ΔU)TR(ΔU) ,

(9)

(10)

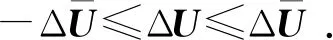
(11)

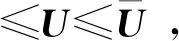
式中：U為控制變量，通常包括發電機電壓整定值、無功補償裝置的安裝/投入量等；ΔU為控制變量的增量；R為權重系數矩陣。注意到因引入了靜態安全域，上述優化模型中無需包含顯式的原始系統模型式(2)-(5)，故求解計算量極小。

需要指出，亦可將節點電壓安全約束、線路熱穩定約束等其他類型的安全約束加入模型式(2)-(5)中，將本文方法和結論拓展至更為綜合的靜態安全上。

1.2 優化模型化簡

目標函數式(9)中概率項ΔP(Z∈ΩSVSR)無顯式解析表達式，故優化模型難以直接求解。為此，引入靜態電壓穩定域邊界的顯式近似，形式如下[9]：

(12)

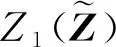
(13)

依據式(7)，將調整控制變量后系統靜態電壓穩定的概率增量寫成條件概率的形式：

(14)

考慮到控制變量U的調整量通常較小，其調整范圍內Z1的概率密度ω1(Z1)變化亦較小，故式中：

(15)

將式(15)代入式(14)中，則調整控制變量后隨機變量位于穩定域中概率的近似增量可由下式給出：

ΔP(Z∈ΩSVSR)≈ΔP*(Z∈ΩSVSR)=

(16)

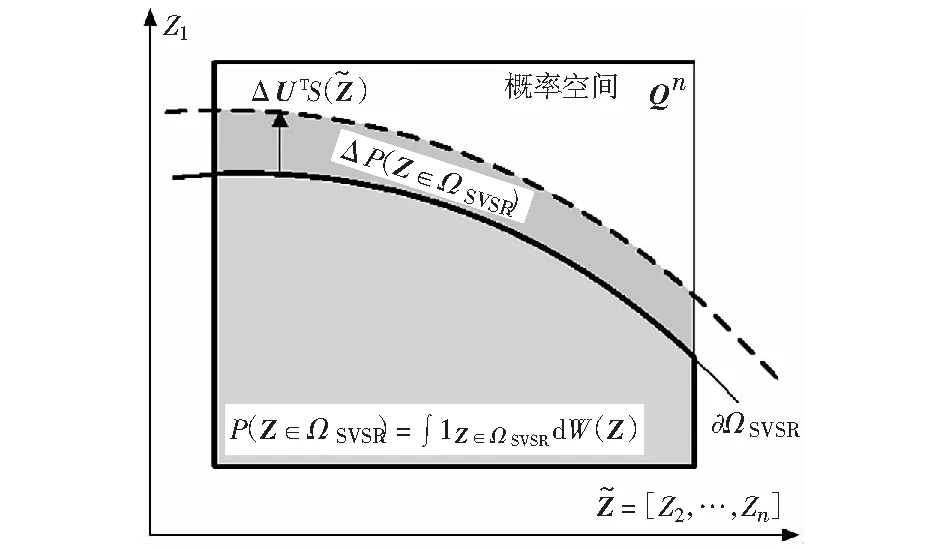
圖1 調整控制變量后隨機向量位于穩定域內概率的示意圖Fig.1 Probability of the random vector staying within the stability region after adjusting control variables

將目標函數式(9)中的概率項替換為近似表達式(16)，則優化模型式(9)-(11)成為一組確定性優化問題，可由經典非線性規劃方法直接求解。

1.3 隨機變量相關性的預處理

風、光等可再生能源的出力存在一定相關性；不同節點負荷相互之間亦可能具有相關性。如前所述，本文所提方法要求各隨機變量間相互獨立，故需事先對非獨立隨機變量進行解耦，具體實現方法可參考文獻[14].

隨機變量維數較高時，為降低計算量，亦可參考文獻[15]對隨機變量進行降維處理。由于隨機變量的解耦和降維并非本文關注重點，故不再贅述。

2 靜態電壓穩定域邊界的多項式逼近

為便于處理隨機變量波動范圍較大時發電機無功越限組合的切換，并在計算穩定域邊界近似表達式的同時得到控制變量對其靈敏度，本節引入一種基于隨機Galerkin方法的參數化非線性規劃問題多項式逼近方法。

2.1 靜態電壓穩定域邊界的參數化非線性規劃模型表示

由靜態電壓穩定極限的定義[14]，將概率空間中的靜態電壓穩定域邊界由如下參數化非線性規劃模型表示[10]：

(17)

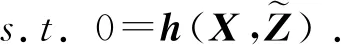
(18)

(19)

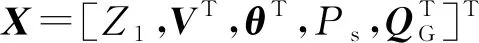
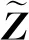
2.2 參數化非線性規劃模型的參數化KKT條件

利用經典原-對偶內點法(primal-dual interior point method,PDIPM)思想將參數化非線性規劃模型式(17)-(19)轉換為參數化非線性代數方程模型。首先，為不等式約束式(19)引入松弛變量：

(20)

使

(21)

并引入對數障礙函數，構造參數化Lagrange函數：

(22)

令參數化Lagrange函數式(22)對各原/對偶變量的偏導為0，可得參數化KKT條件：

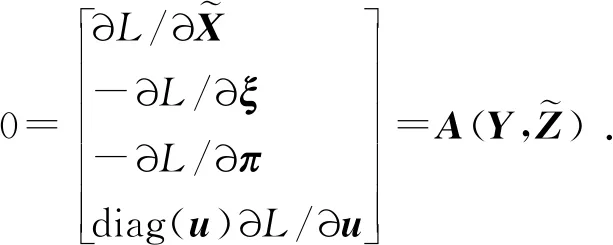
(23)

式中：Y=[XT,uT,ξT,πT]T為所有原、對偶變量構成的向量。

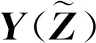
2.3 廣義多項式混沌展開式

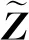
(24)

并取如下張量積作為完整的多項式基函數集：

(25)

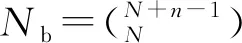
若隨機變量不服從表1給出的任意1種分布類型，則依據等概率原則將其變換至其中任意1種分布類型，繼而進行后續的逼近計算。

表1 隨機分布對應的Wiener-Askey混沌多項式基函數Table 1 Wiener-Askey chaos polynomial basis corresponding to the types of random variables

以式(25)中多項式基函數的線性組合構造Y的gPC展開式，如下：

(26)

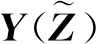
2.4 隨機Galerkin方法

采用隨機Galerkin方法構造投影方程以求解gPC展開式(26)中的待定系數。首先定義期望泛函：

(27)

并基于此定義Hilbert空間

U={h(·)|h:Rn-1→R,〈·,·〉} .

(28)

其上2個元素的內積定義為其乘積的期望：

(29)

將Y中各變量的gPC展開式(26)代入參數化KKT條件式(23)中，并將其向(25)中各個基函數以內積形式(29)作投影以消去隨機變量，形成以展開系數為待定變量的確定性Galerkin投影方程組：

(30)

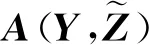
3 算例分析

采用如圖2所示IEEE-39節點系統進行算例分析，計及所有10臺發電機的無功出力約束。恒功率因數增長模式下，初始負荷裕度為51.7%.

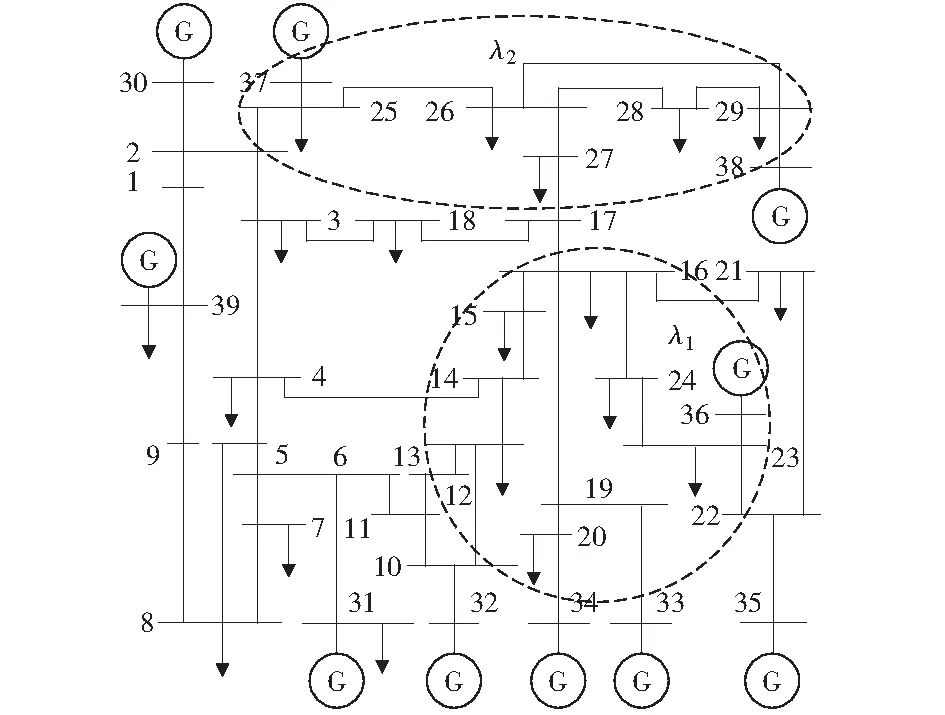
圖2 IEEE-39節點系統接線圖Fig.2 Topology diagram of IEEE 39-bus system

令優化前系統整體負荷增長因子λ為40%.在此基礎上，取區域{13,15,16,17,20,21,23,34}和{25,26,27,28,29}的負荷增長因子作為隨機變量，記為λ1和λ2，并假設λ1服從μ=0,σ=0.1的高斯分布，λ2服從a=2,b=4的Beta分布。采用Monte Carlo模擬驗證準確性時，采樣數NMC取100 000.

3.1 靜態電壓穩定域邊界的逼近結果

首先應用第2節所述方法求取系統靜態電壓穩定域邊界及控制變量對其靈敏度的顯式近似表達式。取gPC展開階數N=5，圖3給出了{λ1,λ2}空間中靜態電壓穩定域邊界的逼近，及其上各點的失穩機理。其中，SNB{30,31,35,37,38}表示發電機{30, 31,35, 37, 38}處于無功越限狀態時發生的鞍結分岔；LIB36-{30,31,35,37,38}則表示發電機{30,31,35,37,38}已處于無功越限狀態時，發電機36無功越限引發的極限誘導分岔。域邊界逼近結果的表達式如下：

(31)

由圖3可知，盡管隨機變量變化時系統的靜態電壓失穩機理發生了多次切換，逼近結果仍很好地貼合了實際邊界。將逼近表達式(29)代入式(7)中，得優化前系統靜態電壓失穩的概率為5.364%，這與Monte Carlo模擬所得結果5.391%相比非常接近，故從另一方面驗證了逼近結果的準確性。這為后續優化提供了堅實的基礎。

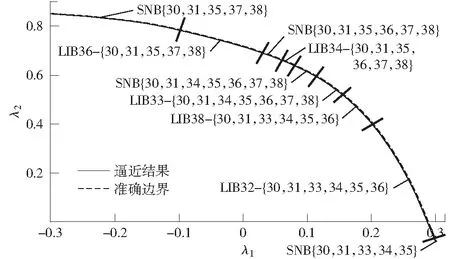
圖3 優化前系統靜態電壓穩定域邊界及其逼近Fig.3 Static voltage stability region boundary before optimization and its approximation

3.2 不確定條件下靜態電壓穩定性的優化

取所有10臺發電機的電壓設定值作為控制變量，其上下限分別設置為0.92和1.08，相較于初始值上下調整幅度限制設置為0.05，目標函數(9)中系數矩陣R=diag([0.1],…,[0,1]T)，進行優化。

優化模型給出的目標函數中，失穩概率降低至2.054%.根據優化結果調整控制變量，以Monte Carlo 模擬計算失穩概率，結果為2.215%，二者基本一致。優化前后系統的靜態電壓穩定域邊界如圖4所示。圖中亦給出了隨機變量的采樣點。顯然，優化結果將靜態電壓穩定域大幅向外拓展，使更多隨機采樣落在了穩定域的內部，故由此大幅降低了系統靜態電壓失穩的概率。

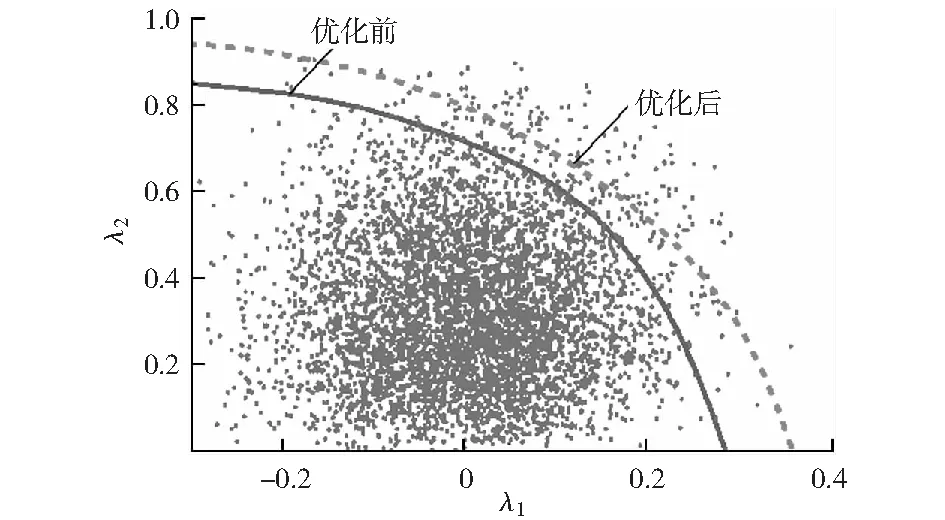
圖4 優化前后靜態電壓穩定域邊界對比Fig.4 Comparison between the static voltage stability region boundaries before and after optimization

優化前后的控制變量，即各發電機節點電壓幅值的設定值則由圖5給出。由圖可知，優化結果提高了32,33,34,36,37,38等6臺發電機的電壓幅值設定值。其中發電機36在優化后達到了1.08的上

限，其余5臺發電機電壓設定值的增量則達到0.05的上限。另有4臺發電機的電壓設定值因其對優化目標的靈敏度為0，故優化結果未對其作任何調整，這表明并非簡單提高發電機電壓設定值即可提高系統的電壓穩定性。

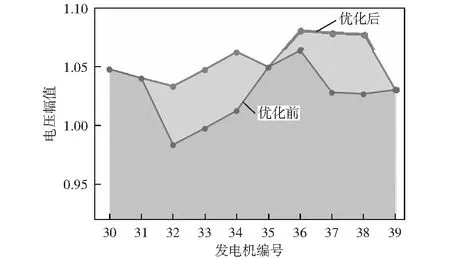
圖5 優化前后發電機節點電壓幅值的設定值Fig.5 Generator voltage magnitude setting values before and after optimization

最后，討論控制變量調整量的權重系數R對優化結果的影響。逐次提高控制量調整量在目標函數中的權重，并采用Monte Carlo模擬求取優化后系統的失穩概率，結果由表2給出。可以看出隨著控制量權重的增加，優化后系統的失穩概率也隨之增加。考慮到增大權重系數可以避免發電機設定電壓的調整幅度過大，權重系數取1左右為佳。

表2 控制變量調整權重對優化目標的影響Table 2 Impact of weight of change in control variables on the optimization objective

4 結論

本文提出了一種基于域的不確定條件下降低電力系統靜態電壓失穩概率的優化方法。結果表明所提方法能夠有效擴展概率空間中的靜態電壓穩定域，從而提升系統的靜態電壓穩定性。

本文以最小化失穩概率作為優化目標，建模仍較為簡單，尚未考慮其與傳統無功優化目標之間的協調。將經濟性因素考慮在內形成綜合的風險-效益指標，提出更為全面的優化模型和方法將是下一步的研究內容。