卷積神經網絡算法分析及圖像處理示例

摘要：卷積神經網絡具有局部結合、權值共享及下采樣等特征，可有效地降低網絡的復雜度減少訓練參數的數目。基于這些優越特性，它在各種信息處理中的性能優于傳統的神經網絡。本文首先介紹神經網絡，進而詳細的分析了卷積神經網絡的原理及結構，包括卷積層、池化層、全連接層，并利用TensorFlow簡單的展示卷積神經網絡用于圖像處理。

關鍵詞：神經網絡;卷積神經網絡;TensorFlow

中圖分類號：TP391文獻標識碼：A

文章編號：1009-3044（2019）34-0176-02

1 概述

神經網絡最早始于1943年的神經生理學家沃倫·麥克洛克和數學家沃爾特·皮茨，他們在根據人腦神經結構提出了感知機神經元模型。1958年Rosenblatt提出了由兩層神經元組成的神經網絡并實現用單個感知機的訓練。該模型數學表示為Y=f（∑w*x），f（x）為激活函數，w為權值向量，x表示模型輸入，Y表示模型輸出。神經網絡實質是一個多層的復合函數。在神經網絡中每一層神經元僅僅與下一層的神經元全連接，而在同一層或跨層的神經元彼此都不連接。這種簡單的神經網絡結構，被稱為多層前饋神經網絡。1986年杰弗里·辛頓和大衛·魯梅爾哈特等人提出了反向傳播（BP）算法系統簡潔地闡述反向傳播算法（BP）在神經網絡模型上的應用。該算法主要分兩步驟：通過正向傳播輸入信號，輸出分類信息;然后通過反向傳播誤差值，鏈式求導反向調整全網權值，讓下一輪的訓練中得到更加準確的輸出。該算法把網絡權值優化的運算量，從原來的與神經元個數的平方成正比，下降到只和神經元數本身成正比，使得權值參數的調整變得簡單易行。該文解決了兩層神經網絡所需要的復雜計算量問題，從而帶動了兩層神經網絡研究的熱潮。近年來，隨著計算力的增強及數據的普及，神經網絡得到了迅速發展，神經網絡的研究進入了白熱化階段，為了獲得更好的結果，神經網絡的應用也越來越廣泛。

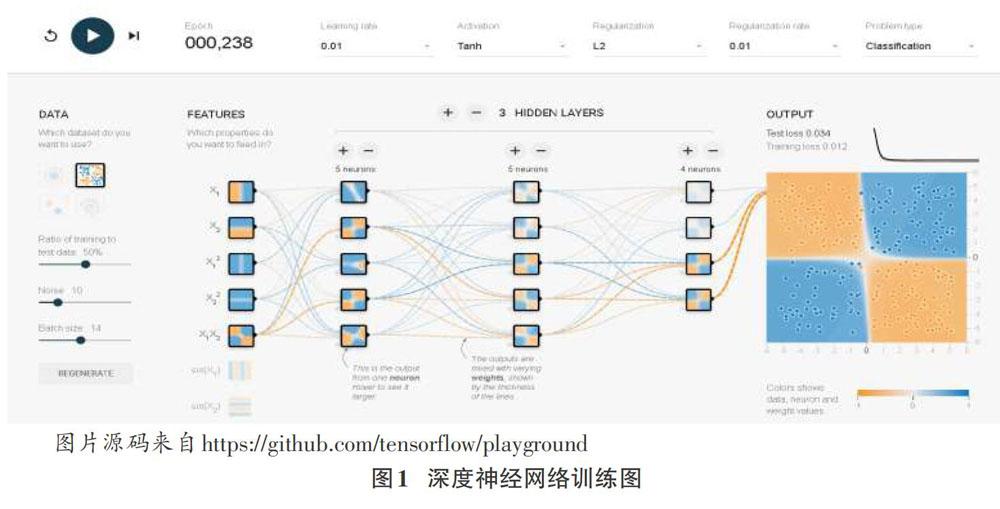
神經網絡的訓練包括設置不同的學習率、激活函數類型、正則類型、正則率、網絡層設置等參數來使訓練達到良好的結果。圖1是根據不同的迭代次數，采用不同的學習率、激活函數、不同的正則類型和正則率、以及不同的網絡層結構進行簡單訓練的demo示例。

2 卷積神經網絡

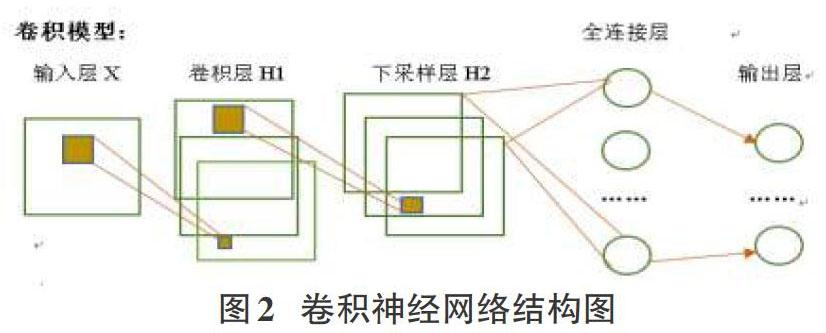
卷積神經網是20世紀60年代Hubel和Wiesel在研究貓腦皮層中用于局部敏感和方向選擇的神經元時發現其獨特的網絡結構可以有效地降低反饋神經網絡的復雜性，進而提出了卷積神經網絡CNN。如今，CNN已經成為眾多科學領域的研究應用熱點之一，特別是在圖像處理領域，由于該網絡避免了對圖像的復雜前期預處理，可以直接輸入原始圖像，因而得到了更為廣泛的應用。K.Fukushima提出的新識別機是卷積神經網絡的第一個網絡實現。卷積神經網本質上是一個權值共享的多層復合函數。該模型的特征使得圖像在平移、扭曲、縮放等操作中具有一定程度的不變性，并具有很強的魯棒性和容錯能力，并且也易于訓練和優化。如圖2，卷積神經網絡分為輸入層、卷積層、下采樣層、全連接層以及輸出層。

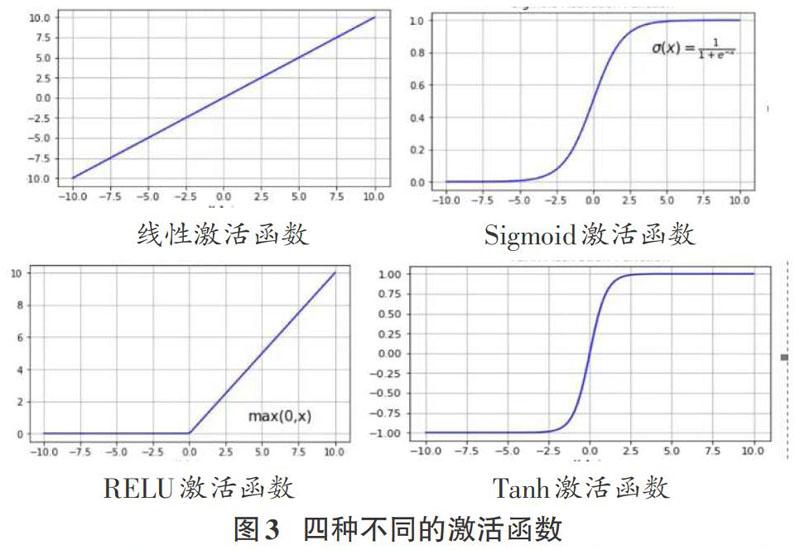
卷積層，卷積層是卷積神經網絡的核心。該層通過“局部感受野”和“權值共享”等神經網絡處理操作。卷積層可對高維數據輸入實施降維處理并自動提取原始數據的核心特征，達到了去偽存真的目的，極大地提高了處理時效。激活層，激活層中的激活函數包括線性激活函數和非線性激活函數。非線性激活函數將前一層的線性輸出進行非線性激活函數處理，從而可達到模擬、逼近任意復雜函數的目的，進而增強網絡的表征能力。常見的三種非線性激活函數包括Sig-moid、Tanh、RELU等，如下圖四種不同的激活函數：

線性激活函數只能進行線性可分，非線性激活函數使得網絡模型可以非線性的表征特征。Sigmoid函數取值范圍為（0，1），它可以將實數映射到（0，1）的區間，用來做二分類。然而，Sig-moid函數在趨近0和1時變化率會變得平坦導致梯度消失。Tanh函數也會出現梯度消失的問題。與sigmoid的區別是，tanh的函數取值范圍為（-l，1），Tanh的梯度值變化較快，在特征相差明顯時具有優越特性。修正線性單元RELU的提出解決了梯度消失問題，該函數具有收斂速度快，且不會產生梯度消失等特性。激活層增強了網絡的表示能力和學習能力。下采樣層，下采樣層其目的是利用數據局部相關性比如圖像數據的局部相似性，通過下采樣獲得少量有用數據來表征數據的主要特征，下采樣層降低了數據的處理規模。由于下采樣具備局部線性轉換不變性，從而增強卷積神經網絡的泛化處理能力。全連接層，通過卷積、激活、池化等多個網絡層處理之后，使得待處理的數據特性發生了顯著變化：輸人數據的維度降低了，非常可觀地減少了全連接層網絡的復雜度;全連接層的輸入數據已不再是冗多繁雜的數據，而是經過反復提純過的主要特征數據，使得最后輸出的結果更加簡練、高效、可處理。在同一特征映射層面上的神經元權值相同，所以卷積神網絡可以并行學習，這是卷積神經網絡的一大優勢。卷積神經網絡從提出至今已經經歷多種變形與融合發展，包括LeNet、AlexNet、FNet、VGG、NIN、ResNet、GoogleNet、SENet等經典的結構。

3 TensorFlow及圖像處理上的應用

TensorFlow是基于張量流的機器學習計算框架。它是基于數據流圖作為核心抽象，采用聲明式編程范式，即程序像一種數學模型表達，輸入自變量，輸出因變量。該范式的程序通過用戶設計與組合表達式來實現計算，更適合于神經網絡模型。TensorFlow具有代碼可讀性強、引用具有一定的透明性，提供了預編譯優化的能力等優越特性。TensorFlow也提供了大量的庫函數。通過tf.nn.conv2d可以實現卷積計算。CNN主要用來識別位移、縮放及其他形式扭曲不變性的二維圖形。如下圖采用不同核函數得到的圖片。圖左一采用單位矩陣卷積核得到了原圖，相當于未對圖像進行任何操作。圖左二到圖左四分別采用Kerne12、kerne13、kerne14訓練得到。

4 結論

隨著CNN的發展，CNN網絡的融合與變形越來越多，CNN的理論發展日趨成熟。CNN的理論及實踐發展迅速，這與我們計算力GPU的發展及大數據的普遍應用密不可分，同時也得益于不斷開源的工具。CNN高效快捷的應用已成普遍，在圖像分類、物體檢測、物體追蹤、姿態預估、文本檢測識別、視覺、行動識別、場景標記等領域都得到了廣泛的應用，并且將獲得較高準確率。未來人們不僅將會這些應用場景中獲得更高的準確率，同時，也將會兼顧應用處理的速度與時效。

參考文獻：

[1] Williams D，Hinton G.Learning representations by back-prop-agating errors [J]. Nature，1986，323 （6088）：5 33-5 38.

[2] Rodolfo Bonnin.Building Machine Learning Projects with Ten-sorFlow[M].Packt Publishing，2016，12.

[3]張玉宏.深度之美[M].北京：電子工業出版社，2018.

【通聯編輯：梁書】

收稿日期：2019-10-12

作者簡介：劉中雨，男，碩士，主要研究方向為機器學習與數據科學。