FMEA失效模式與影響分析研究分析
——基于2015年以來 SCI/SSCI期刊文獻

尚珊珊 高明瑾

(上海外國語大學 國際工商管理學院，上海 200083)

0 引言

當前越來越多的組織和企業(yè)進行風險評估，F(xiàn)MEA失效模式與影響分析相關(Failure mode and effect analysis, FMEA)是挖掘潛在風險，進行風險評估并對風險進行優(yōu)先定級的一種有效邏輯分析方法。FMEA失效模式與影響分析是最早由美國航空航天行業(yè)于20世紀60年代根據(jù)其可靠性和安全性需求所提出的一種系統(tǒng)性和結(jié)構性的方法。FMEA是識別發(fā)現(xiàn)及去除系統(tǒng)、設計、過程或服務中問題、錯誤及潛在風險的一種有效且非常流行的工業(yè)技術方法。與其他關鍵要素分析工具不同，F(xiàn)MEA的目標是查找系統(tǒng)中所有可能的失效模式，分析其影響及產(chǎn)生的原因，進而從根本上消除產(chǎn)生問題的根源，而非在問題發(fā)生后提出解決方法。FMEA需要跨部門、不同領域的專家合作，系統(tǒng)分析失效模式、影響、原因、當前控制方法，從而提出消除措施。FMEA是保障產(chǎn)品、過程安全性和可靠性的重要方法，廣泛應用于航天航空、汽車制造、核工業(yè)，以及醫(yī)療服務等行業(yè)領域，是風險分析的重要手段。

FMEA自提出以來，由于簡單易用受到了廣泛歡迎，很多專家學者將其應用在不同行業(yè)領域中進行風險分析，并針對原因提出消除風險方案措施。但是，F(xiàn)MEA本身的缺陷也不容忽視。近年來有很多專家學者致力于研究對FMEA方法的改進，大都從權重和群組決策角度出發(fā)。文章詳細梳理了近三年SCS/SSCI期刊庫中FMEA相關文章，深入分析了FMEA近三年的研究特點及發(fā)展趨勢。

1 FMEA文獻基本分析

1.1 FMEA相關研究的作者及單位分析

文章對SCI/SSCI期刊庫進行檢索，只分析直接研究FMEA的相關文獻并且只限于分析期刊文獻，因此以標題對期刊庫近三年的文獻進行檢索，檢索結(jié)果只有英語、法語、德語等，沒有中文。由于作者不懂其他語種，而且其他語種文獻也很少，所以文章只限于英文文獻。因此，文章檢索條件如下：

標題: (FMEA or failure mode and effect analysis)；精煉依據(jù)：文獻類型: (ARTICLE OR REVIEW)；AND 語種: (ENGLISH)；時間跨度: 2015—2018；索引: SCI-EXPANDED, SSCI, A&HCI, CCR-EXPANDED, IC。文章進一步對文獻進行檢查，對于非failure mode and effect analysis的研究文獻進行剔除，最后選取相關文獻109篇。

1.1.1歷年期刊文章數(shù)量

根據(jù)表1可以看出，文章檢索日期截至2018年1月底，2015—2017年，F(xiàn)MEA文獻研究逐年增長，2018年數(shù)據(jù)不全，但是僅1月份已經(jīng)可以從文獻庫檢索到的文章已有5篇。

表1 年度發(fā)表論文數(shù)

1.1.2作者分析

文章對109篇文章作者進行分析，109篇文章中，僅有4篇為獨立作者，其他均為合作論文，其中影響力較大的作者如圖1所示，為Liu H.C.，J.X.You，C.H.Jong, Lolli F，文章對影響力的定義為這109篇中論文的發(fā)表數(shù)量及論文引用的數(shù)量。

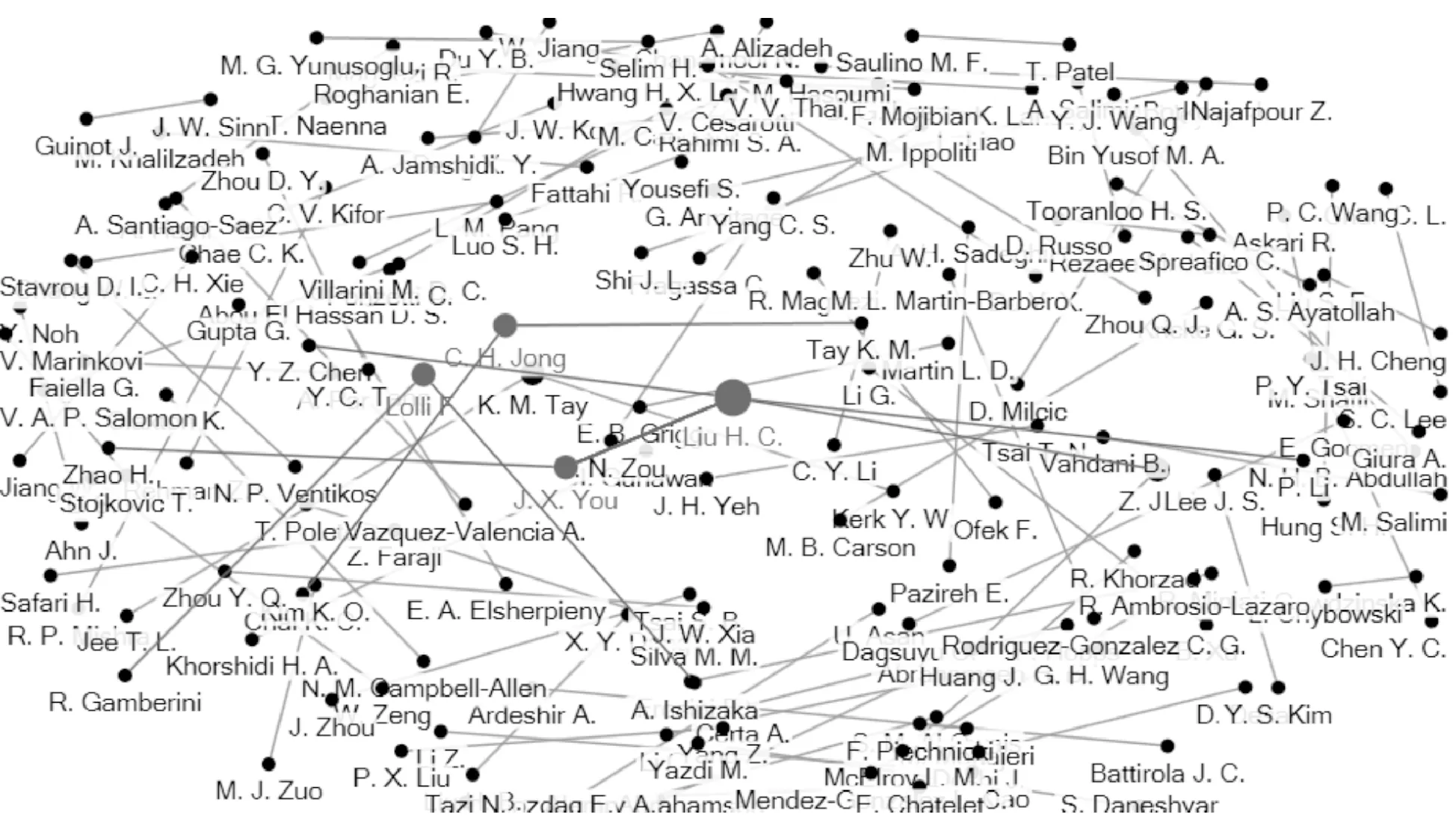
圖1 作者分析

1.1.3作者單位分析

對作者單位的分析如圖2所示，節(jié)點帶環(huán)的為本單位(同一個大學或機構)內(nèi)部合作。109篇文章中，55篇文章為不同單位，54篇為同一個單位，不同單位間的合作占50%。其中，比較有影響力的單位如圖2所示，節(jié)點越大代表影響力越大。

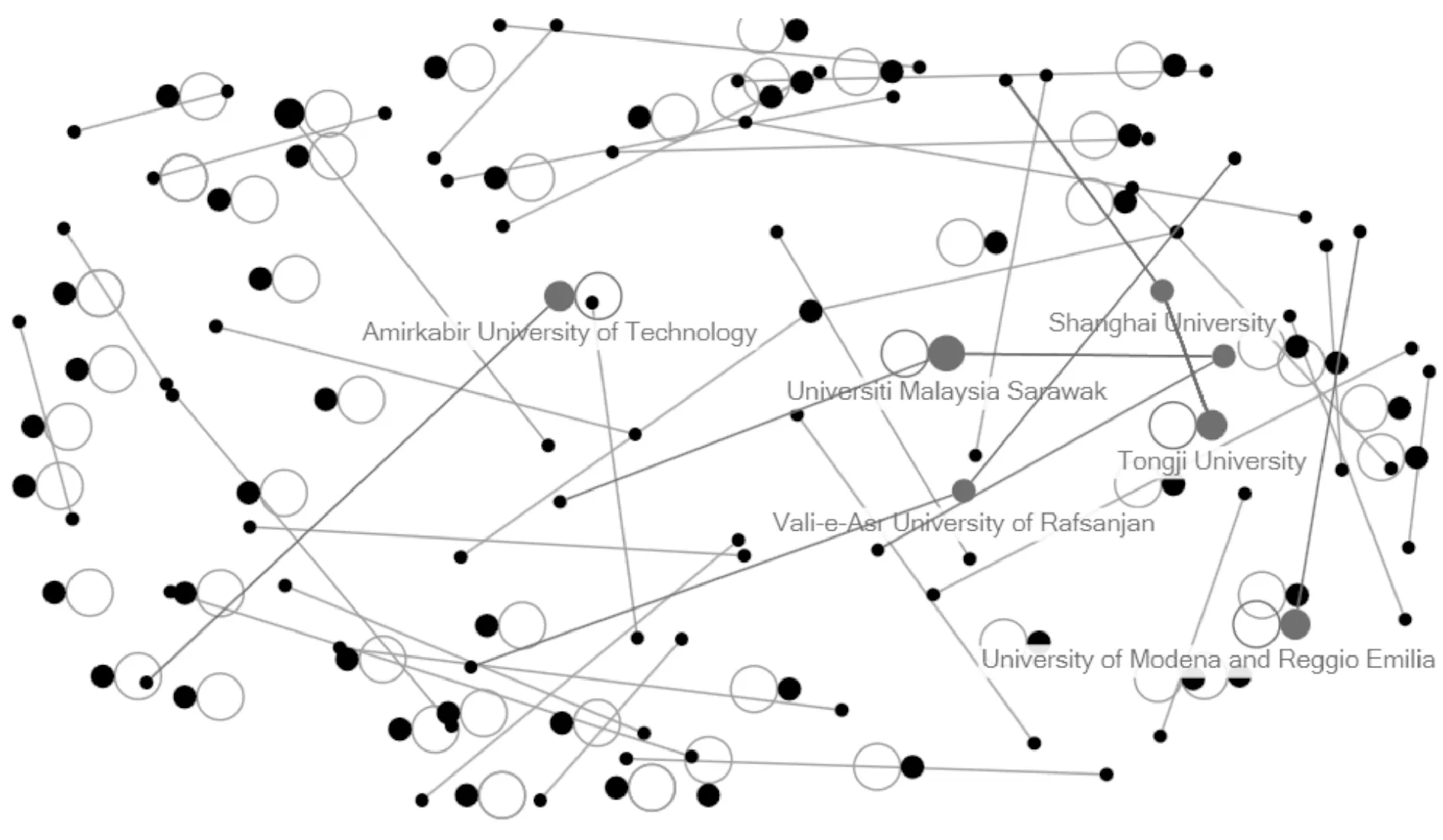
圖2 作者單位分析

1.1.4國家分析

論文作者國家如圖3所示，節(jié)點帶環(huán)表明論文為本國內(nèi)部合作。110篇論文中不同國家合作的僅有13篇，有些比如China、USA間合作可能不只一次。可以看出，論文發(fā)表合作主要還是在本國內(nèi)部，跨國交流合作的很少。圖3中，節(jié)點越大表示影響力越大，可以看到發(fā)表FMEA相關論文影響力較大的國家主要有China，Iran，Malaysia，Canada，USA，Italy，UK，Republic of Korea等。

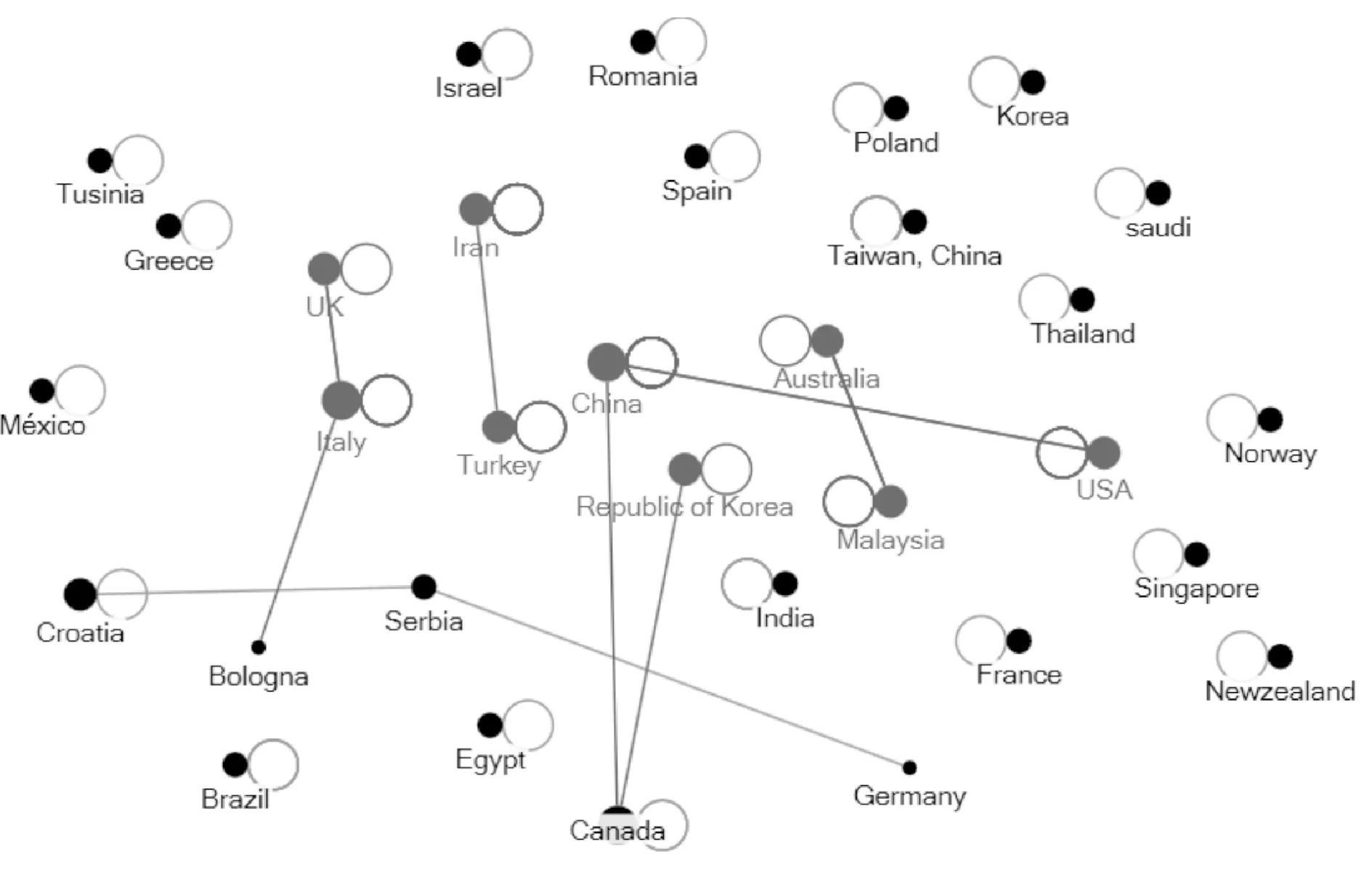
圖3 作者國家

1.1.5來源期刊分析

相關論文主要來源期刊如表2所示，表2中文章整理發(fā)表兩篇以上相關論文的期刊。可以看出，QualityandReliabilityEngineeringInternational發(fā)表相關論文最多，三年間發(fā)表FMEA論文8篇，其次為ReliabilityEngineering&SystemSafety、InternationalJournalofQuality&ReliabilityManagement及AppliedSoftComputing。可以看出，來源期刊多為質(zhì)量管理主題期刊，但是由于很多FMEA研究論文是通過各種技術手段對FMEA方法進行改進，因此，AppliedSoftComputing期刊相關論文也較多。

表2 來源期刊

1.2 FMEA相關研究主題分析

針對FMEA的研究主要有兩大類主題，一是對傳統(tǒng)FMEA方法的改進，一是將FMEA相關方法應用于各領域之中以找出過程中的關鍵風險點從而對其進行改進，具體改進方法及應用會在第3節(jié)和第4節(jié)進行詳細介紹。近三年相關主題研究及趨勢如表3所示。

根據(jù)表3可知， 2015年對FMEA方法改進的研究占60%，2016年占54%，2017年占28%。可以看出，到2017年將FMEA或已有的FMEA改進方法應用于各領域之中已是學者研究的主要關注點，針對FMEA研究方法改進的相關研究所占比例已顯著下降。同時也反映出，F(xiàn)MEA方法具有較強的實踐性，可以有效應用于各實踐領域。FMEA方法的主要優(yōu)勢在于： (1) 便于理解與實施； (2) 其本質(zhì)為定性分析方法，但是同時結(jié)合定量分析，在一定程度上規(guī)避了全定性分析的主觀性；(3)根據(jù)RPN值對失效模式風險進行排序，可以幫助產(chǎn)品設計、生產(chǎn)制造過程、工業(yè)工程鑒別主要改進因素，幫助其實施過程改進。

表3 近三年的研究主題及發(fā)展研究

2 FMEA主要方法改進分析

2.1 傳統(tǒng)FMEA方法及主要問題

FMEA主要根據(jù)RPN值對風險進行排序，其中RPN= S*O*D，S、O、D分別為Severity、Occurrence，以及Detectivity的首字母，代表嚴重程度、發(fā)生概率，以及易于發(fā)現(xiàn)概率，其判別等級如表4所示。

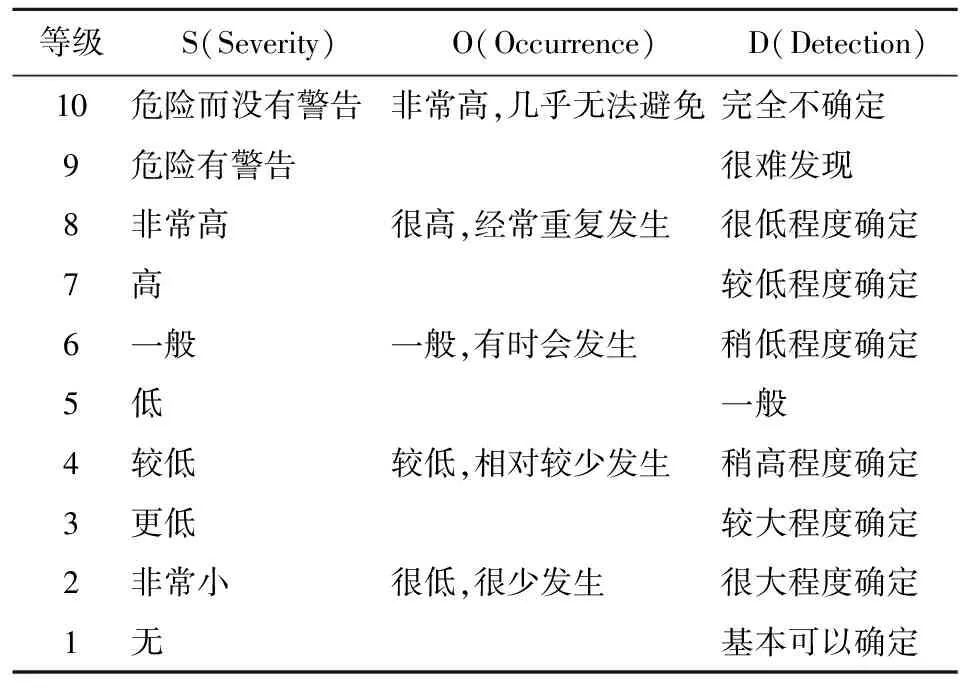
表4 S、O、D值

FMEA傳統(tǒng)方法的過程如下：(1)組建FMEA專家組；(2)收集過程功能信息；(3)分析潛在失效模式；(4)分析每個失效模式所造成的結(jié)果；(5)分析每個失效模式的原因；(6)確定每個失效模式的S、O、D值；(7)計算RPN值，并根據(jù)RPN值對失效模式進行排序；(8)對風險較大的失效模式進行改進。

盡管FMEA簡單且受歡迎，但是FMEA方法也存在一些問題：(1)FMEA基于RPN值排序，但RPN值是由S、O、D三者相乘而得，不同的S、O、D值可能得到相同的RPN值，比如(5，2，6)和(4，5，3)具有相同的RPN值，傳統(tǒng)FMEA中僅有200個RPN值具有唯一性，即唯一的S、O、D值與之相對應；(2)沒有考慮S、O、D的權重，認為這三個權重一樣，但實踐中不同系統(tǒng)中這三個方面的權重一般不同；(3)僅考慮這三個方面的因素，而其他方面的很多因素其實也很重要，但FMEA中卻沒有考慮；(4)1～10這十個等級評判比較具有主觀性，不容易界定；(5)RPN值的計算缺乏系統(tǒng)的科學根據(jù)，S、O、D中一個值的微小波動可能會造成RPN值的顯著改變。

2.2 FMEA方法改進發(fā)展分析

根據(jù)文章所檢索的文獻，主要改進所采用的方法整理如表5所示。根據(jù)表5中整理結(jié)果可以看出，針對FMEA方法缺陷，采用模糊方法是總體思路，基本所有改進方法都會首先考慮模糊化。經(jīng)典模糊化方法有模糊理論及灰色理論(Fuzzy theory & Grey theory)，而采用模糊理論的占絕大多數(shù)。同時，由于FMEA需要專家評判，因此很多文獻會考慮采用語義不確定性進行度量(Linguistic)。針對FMEA各要素權重一樣的缺陷，文獻多采用AHP、熵(Entropy)等改進確定各要素權重，針對傳統(tǒng)FMEA各專家簡單結(jié)果匯總的缺陷，很多研究根據(jù)FMEA本質(zhì)也屬于多目標決策(Multi-criteria decision making, MCDM)問題，采用MCDM相關的方法對其進行改進，主要有TOPSIS、VIKOR、DEMATEL、MULTIMOORA相關及在相關基礎上發(fā)展的方法。由于FMEA也是專家決策，因此一些研究基于決策推理角度對FMEA方法進行改進，多采用Dempster-Shafer Theory相關及在相關基礎上發(fā)展的方法。

從總體方法發(fā)展來看，根據(jù)文章所采集的SCI/SSCI數(shù)據(jù)庫中的相關期刊文獻，2015年和2016年方法改進文章中都有很多為考慮模糊環(huán)境下應用一種方法以改進FMEA而且主要采用傳統(tǒng)數(shù)學或決策方法，如應用Fuzzy TOPSIS、Fuzzy DEMATEL、Fuzzy inference system。2016年，更多研究結(jié)合兩種方法以改進FMEA，而且較之2015年更多學者關注到詞語的模糊含義，即語義linguisitic及Intuitionistic Fuzzy Sets的應用，并且2016年一些學者使用Dempster-Shafer Theory。到2017年，研究所采用的方法更為復雜，基本均為同時采用兩種方法改進FMEA，并且所采用的方法很多基于之前方法的進一步發(fā)展，如D-number(擴展的Dempster-Shafer Theory)、IVIFSs(Intuitionistic Fuzzy Sets的擴展，Interval Value Intuitionistic Fuzzy Sets)、IFIS(Fuzzy inference system的擴展，Interval Fuzzy inference system)、linguistic distribution(linguisitic方法擴展)。同時，2017年一些學者應用MULTIMOORA于FMEA方法改進之中。2018年1月的兩篇FMEA方法改進文獻中，一篇為全過程模糊化MULTIMOORA結(jié)合AHP的應用以改進FMEA，另外一篇則從一個新的角度去看待FMEA，將整體過程看成層次化的過程，利用概率方法分析每段過程下基于FMEA的風險評判。

FMEA改進方法中也有一些其他方法的采用，如QUALIFLEX、ELECTRE，這仍是基于群組決策或多目標決策角度下的改進。同時，值得注意的是，已有學者試圖采用一些機器學習方法如data mining、ontology、K-means、self-organizing map對初始原因數(shù)據(jù)或風險結(jié)果數(shù)據(jù)進行一些處理，但是仍處于對初始數(shù)據(jù)或結(jié)果數(shù)據(jù)的聚類合并分析，且考慮大數(shù)據(jù)環(huán)境下應用機器學習或人工智能方法改進FMEA的方法很少。

表5 改進方法的發(fā)展

2.3 FMEA主要改進方法

根據(jù)近三年的相關研究文獻，主要的改進方法步驟如下所示。

2.3.1直接模糊決策系列

直接模糊決策系列主要是直接將一些模糊方法應用于FMEA之中，如Fuzzy AHP、Grey Theory，以及Fuzzy TOPSIS等，所應用的模糊數(shù)基本都是三角模糊數(shù)，F(xiàn)uzzy AHP主要是確定模糊權重，Grey Theory的利用主要是通過GRA(灰色相關系數(shù))進行排序，F(xiàn)uzzy TOPSIS主要是基于模糊評價值利用TOPSIS方法進行排序。與Fuzzy TOPSIS方法類似的還有Fuzzy VIKOR、Fuzzy DEMATEL方法。主要相關直接模糊決策系列的方法過程整理如表6所示。

表6 直接模糊決策系列改進方法

2.3.2Linguistic系列與Intuitionistic Fuzzy Sets系列

由于傳統(tǒng)的FMEA中1～10分的評分相對于日常語言評價來說更為困難，因此一些專家學者通過運用語言變量對傳統(tǒng)FMEA方法進行改進。Liu H. C.(2015)使用Interval 2-Tuple Linguistic Variables方法對專家語言評價進行量化，而后通過灰色關聯(lián)系數(shù)進行排序決策。Zhou. Y. Q(2016)則使用語言加權幾何運算(LWG, Linguistic weighted geometric operator)對專家評價進行匯總計算后對FMEA進行改進。Kok Chin Chai et al.(2016)利用interval type-2 fuzzy sets對專家評價語言進行模糊化處理，并基于此計算RPN值并進行排序。Huang J. et al.(2017)則是利用語言分布(linguistic distribution assessments)方法對專家評價語言進行模糊量化處理，而后利用改進的TODIM方法對專家評價進行整合，從而確定失效模式風險的先后次序。

IFS(Intuitionistic Fuzzy Sets, IFS)是Atanassov教授最早于1983年提出的一種模糊信息的概念，把只考慮隸屬度的Zadeh 經(jīng)典模糊推廣為同時考慮真隸屬度、假隸屬度和猶豫度這三方面信息的直覺模糊集，是傳統(tǒng)模糊集合的一般化。基于此，結(jié)合區(qū)間所提出的IVIFS(Interval Value Intuitionistic Fuzzy Sets, IVIFS)則是對IFS的進一步擴展。因此，IFS及IVIFS通常被研究者用來代替?zhèn)鹘y(tǒng)模糊化方法應用于FMEA方法改進之中，利用IFS或IVIFS對專家評分進行處理和運算。

Liu H.C.(2015)則是利用IFS對專家評價進行模糊化處理后，利用TOPSIS方法對專家評價進行綜合，進而對風險進行排序。TOORANLOO H S, AYATOLLAH A S(2016)直接利用IFS對專家評價進行模糊化處理，并利用IFS系統(tǒng)中的模糊運算對專家評分進行整合運算，并考慮指標權重建立專家決策矩陣，通過計算與最優(yōu)值和最差值間的距離，進而通過計算鄰近度系數(shù)(closeness coefficient)對風險進行排序。而后，作者又在此文章的基礎上進一步改進，改進之處主要在模糊化處理和指標權重的確定上，TOORANLOO H S, AYATOLLAH A S.(2017)用IVIFS對專家評價進行模糊化處理，利用熵(entropy)得出指標權重。

2.3.3Dempster-Shafer Theory系列

Dempster-Shafer Theory，有些文獻中直接稱為evidence theory或D-S理論，起源于20世紀60年代的哈佛大學數(shù)學家Dempster A.P，它利用上、下限概率解決多值映射問題。Dempster的學生shafer G.對證據(jù)理論做了進一步發(fā)展，引入信任函數(shù)概念，利用“證據(jù)”和“組合”來處理不確定性推理的數(shù)學方法。D-S理論是對貝葉斯推理方法的推廣，不需要知道先驗概率，能夠很好地表示“不確定”，被廣泛用來處理不確定數(shù)據(jù)。該理論的核心為Dempster合成規(guī)則，可以將多個主體(可以是不同的人的預測、不同的傳感器的數(shù)據(jù)、不同的分類器的輸出結(jié)果等)相融合。因此，很多專家學者將此理論應用于FMEA中，根據(jù)本文的文獻檢索結(jié)果可以看到，43篇FMEA改進方法文獻中，有7篇約占16%的方法改進研究是基于該理論進行改進的。

理論主要的基本概念有：基本概率分配(BPA, Basic Probability Assignment)。設U為識別框架，則函數(shù)m:2u→[0,1]滿足下列條件：(1)m(φ)=0; (2)∑A?Um(A)=1時，稱m(A)=0為A的基本賦值，m(A)=0表示對A的信任程度，也稱為mass函數(shù)。信任函數(shù)(Bel,BeliefFunction),Bel:2u→[0,1] ,Bel(A)=∑B?Am(B)=1(?A?U) ,表示A的全部子集的基本概率分配函數(shù)之和 。似然函數(shù)(Pl,plausibilityFunction)。似然函數(shù)表示不否認A的信任度，是所有與A相交的子集的基本概率分配之和,Pl(A)=1-Bel(A)=∑B?Um(B)=∑B?A-m(B)= ∑B∩A≠φm(B) 。 信任區(qū)間，[Bel(A)，Pl(A)]表示命題A的信任區(qū)間，Bel(A)為下限，pl(A)為上限。

D-S證據(jù)理論的融合規(guī)則 ：m個mass函數(shù)的Dempster合成規(guī)則如下所示，其中K稱為歸一化因子，1-K即∑A1∩,…,∩An=φm1(A1)m2(A2),…,mn(An)反映了證據(jù)的沖突程度，融合原則如式(1)所示。

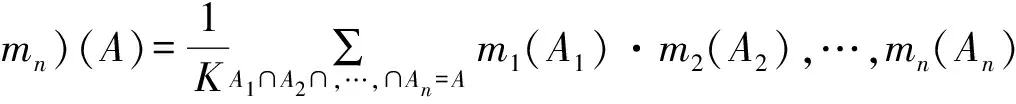
(1)

D-S理論也存在一些局限如無法解決證據(jù)沖突嚴重和完全沖突的情況，無法辨識模糊度，證據(jù)要求獨立性，集合要可完全劃分等。

現(xiàn)有利用D-S理論進行FMEA改進的文獻中，基本都是利用D-S理論的組合規(guī)則對多個專家的意見進行組合，結(jié)合利用其他方法來確定BPA、Bel、Pl，而為解決D-S無法解決證據(jù)嚴重沖突的情況，文獻通常會采用Pignistic概率轉(zhuǎn)換(Pignistic probability transformation)。Deng et al.(2016)即引入Generalized Evidence Theory于FMEA中。該理論在D-S理論的基礎上發(fā)展而來，采用的是GBPA(Generalized Basic Probability Assignment, GBPA)和GCR (Generalized Combination Rule, GCR)合并規(guī)則以改進傳統(tǒng)D-S 理論只能應用于完全信息的局限。Guo Jian (2016)同時采用IFS( Intuitionistic Fuzzy Sets) 和D-S理論于FMEA方法改進中，F(xiàn)MEA專家團隊的評價也并非簡單1～10分評價，而是利用語言評價(Linguistic Term)，將專家的評價語言利用IFS轉(zhuǎn)化成相應的模糊數(shù)據(jù)Ifns (Intuitionistic Fuzzy Numbers, Ifns)，并將IFNs轉(zhuǎn)換成D-S理論中對應的BPA值，利用Jousselme distance確定專家權重，進而利用D-S融合規(guī)則對專家意見進行融合，并利用D-S判決規(guī)則進行判斷以形成最終評價排序。Yuxian Du et al.(2016)則利用Pignistic 概率轉(zhuǎn)換方法確定BPA，pignistic概率轉(zhuǎn)換是解決沖突所提出的一種轉(zhuǎn)換方法，繼而利用D-S融合規(guī)則對專家意見進行融合并對最終FMEA結(jié)果進行排序。Zhen Li et al.(2017)首先利用語言評價(linguistic term)代替?zhèn)鹘y(tǒng)FMEA的10分評價，為每個語言評價設置模糊隸屬度函數(shù)，對應的模糊值為BPA值，確定每個評價指標的權重，結(jié)合權重利用融合規(guī)則對專家意見進行融合，而后對融合后的結(jié)果值進行Pignistic概率轉(zhuǎn)換，最后進行評價排序。Wen Jiang et al.(2017)的FMEA方法也使用D-S理論進行融合，利用Pignistic概率轉(zhuǎn)換以改進D-S理論證據(jù)沖突嚴重時的局限，但是其對語言模糊化及融合處理的方式都不同，以往是首先將每個專家的評分模糊化而后利用D-S理論進行融合，但是Wen Jiang et al.(2017)則是首先將所有的專家評分整理得出每個失效模式在1～10的隸屬度，而后根據(jù)其建立L(低)、M(中)、H(高)隸屬度函數(shù)，利用(模糊隸屬度函數(shù)*各級評價隸屬度)模糊映射得出每個失效模式的S、O、D的L、M、H映射值，通過D-S融合規(guī)則計算每個模式的m(O⊕S⊕D)(Ai)值，其中Ai?U，U={L,M,H}，計算出的值再利用Pignistic概率轉(zhuǎn)換，進而基于此進行排序?qū)Ρ取inyang Deng, Wen Jiang(2017)利用梯形模糊化函數(shù)對專家評分進行模糊化后，利用基于D-S理論擴展的D數(shù)據(jù)進行融合。Antonella Certa et al.(2017)則考慮專家評分時的認知不確定性(epistemic uncertainty)，即專家可能認為并不是1～10的某一個確定值，而是處于某一區(qū)間內(nèi)，比如[1,2]，利用區(qū)間對專家評分進行處理，然后基于D-S理論融合規(guī)則進行專家意見融合并排序。

2.3.4MULTIMOORA方法系列

MULTIMOORA(multiple multi-objective optimization by ratio analysis, MULTIMOORA)方法是Brauers, Zavadskas (2010) 基于MOORA(multi-objective optimization by ratio analysis, MOORA)所提出的多目標決策方法，該方法已經(jīng)應用于很多目標決策優(yōu)化問題，但是在FMEA中的應用還較少。

根據(jù)文章檢索結(jié)果，2015年以來SCI/SSCI期刊文章中，Liu H.C.(2017)首次利用MULTIMOORA對FMEA方法進行改進。其利用IVIFS對專家評價進行模糊化處理，利用entropy確定評價指標權重，最后利用MULTIMOORA對專家意見進行綜合，從而得出風險排序。Reza Fattahi, Mohammad Khalilzadeh(2018)則利用傳統(tǒng)模糊方法三角模糊數(shù)處理專家評分，利用AHP確定指標權重，最后利用MULTIMOORA對專家意見進行綜合后得出風險排序。

2.4 FMEA方法改進點總結(jié)

綜合以上分析可以看出，研究學者對FMEA方法的改進主要在專家評價處理、評價指標權重確定、以及群組決策上，整理如表7所示。由于傳統(tǒng)1～10評分比較難以確定，自然語言更利于專家評價，并且評價通常不是一個確定值，因此對于專家評價主要集中于專家評價自然語言的模糊化。而由于傳統(tǒng)FMEA方法認為S、O、D三者權重一致，通常與現(xiàn)實不符合，因此一些研究利用AHP、Entropy等來確定評價指標權重。此外，F(xiàn)MEA方法實質(zhì)也是多目標決策也是群組決策，因此很多專家學者應用多目標決策或群組決策方法對模糊化處理后的專家評分進行綜合。文章經(jīng)常同時從這三個方面進行改進。

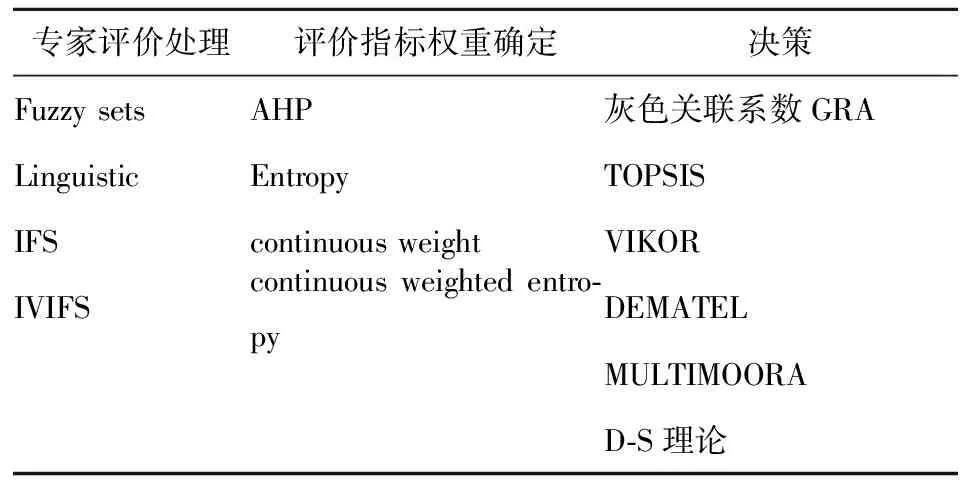
表7 FMEA方法主要改進點

3 FMEA主要應用研究分析

根據(jù)文章檢索結(jié)果，109篇文章中66篇在于FMEA方法應用，可以看到多數(shù)FMEA相關文章主要利用FMEA方法應用于行業(yè)之中進行風險分析，從而進一步為消除風險進行過程改進。應用文章中的主要應用領域整理如表8所示，可以看出應用領域最多的是醫(yī)療行業(yè)，僅醫(yī)療行業(yè)應用FMEA的文章就占36%。

表8 應用領域

根據(jù)對這66篇應用文獻的分析可知，文獻所采用的方法基本是傳統(tǒng)FMEA方法，很少復雜結(jié)合多種方法的FMEA模型，僅有三篇采用復合FMEA模型。其中，Yazdi, M., et al. (2017)、Gupta, G. and R. P. Mishra (2017)采用相對簡單的Fuzzy FMEA，即僅專家評價采用傳統(tǒng)模糊隸屬度函數(shù)進行模糊化處理，其他權重、決策等沒有結(jié)合采用其他改進方法。Rahimi, S. A., et al. (2015)則結(jié)合利用GRA灰色關聯(lián)系數(shù)進行最后排序。一些文章會同時采用兩種方法分別對風險進行評價，而后綜合分析兩種方法的結(jié)果，如Tsai, S. B., et al. (2017)同時利用FMEA和DEMATEL兩種方法對過程進行風險分析。

但是總體上，應用文章基本都是采用最簡單的傳統(tǒng)FMEA方法，很少采用FMEA的改進方法，而且應用文章的關注點主要是原因查找、分析及改進。可以看出，盡管傳統(tǒng)FMEA方法存在一定缺陷，而且也已經(jīng)有很多FMEA改進方法，但是由于傳統(tǒng)FMEA方法的簡單、實用、易操作，反而是應用領域中最受歡迎、最廣泛采納的應用。應用文章中，關注點多在于FMEA過程中風險原因的查找分析，以及最后的改進措施。

4 結(jié)語

文章對近三年SCI/SSCI期刊文獻中的FMEA研究進行了詳盡梳理，深入分析了FMEA主題文獻主要的研究特點與發(fā)展趨勢，詳細分析說明了FMEA方法的主要改進點及近三年的主要改進方法，并梳理FMEA方法的主要應用領域及應用特點。文章研究發(fā)現(xiàn)，F(xiàn)MEA方法改進主要基于專家語言、權重，以及多目標群組決策角度，但是文章對FMEA相關應用文獻的研究發(fā)現(xiàn)應用中仍主要偏向于使用傳統(tǒng)的最為簡單的FMEA方法。文章對進一步研究FMEA及應用FMEA相關研究及實踐有輔助支持作用。