一種改善永磁同步電機性能的多目標優化方法

王明星,王愛元,李軼華,莊石榴

(上海電機學院,上海 201306)

0 引 言

在設計電機時,為了在一定程度上提高永磁電機的效率,通常對永磁電機的結構參數進行優化[1-2],但這些參數在影響永磁電機效率的同時也會影響永磁電機的噪聲值[3-4]。因此,在保證電機轉矩一定的情況下,對永磁電機的效率和噪聲同時進行優化，具有重要的實際意義。

1 永磁同步電機噪聲的求解過程

永磁同步電機噪聲計算涉及到三個場的耦合[5],在ANSYS Maxwell中,利用該電機全模型,計算定子內表面徑向磁拉力,將其作為激勵源耦合到ANSYS Mechanical中進行該電機三維定子諧響應分析,然后將諧響應分析結果作為激勵源耦合到ANSYS Mechanical ACT中進行三維聲場分析。變頻器供電的永磁電機噪聲頻率主要分布在開關頻率及其倍頻附近[6],考慮到計算內存,選取頻率范圍為0～10 kHz,其中開關管的頻率3 kHz,所以噪聲在3 kHz，6 kHz，9 kHz處表現得最明顯。為了便于算法的優化,本文選取6 kHz處的噪聲值作為后續的一個優化目標。

2 永磁同步電機效率的求解過程

參考現有的永磁電機結構參數，將其確定為電機初始參數值,然后通過ANSYS Maxwell軟件對電機進行建模，電機采用PWM供電,開關管頻率為3 kHz。通過軟件計算永磁電機轉矩平均值,結合電機的轉速，從而求出永磁電機的輸出功率;利用軟件求出永磁電機的鐵耗，然后根據該電機的規格乘以鐵耗修正系數，得到最后的鐵耗值；利用軟件求出永磁體的渦流損耗；機械損耗按該電機規格由經驗值所得；計算定子繞組的銅耗，最后將損耗與輸出功率相加得到電機的輸入功率，從而計算電機的效率。

3 參數優化過程

3.1 初始參數的計算

本文采用ANSYS分析軟件對永磁同步電機進行噪聲和效率分析，采用4極24槽，功率為550 W的小功率永磁同步電機作為算例，額定轉速為1 500 r/min,主要參數如表1所示。

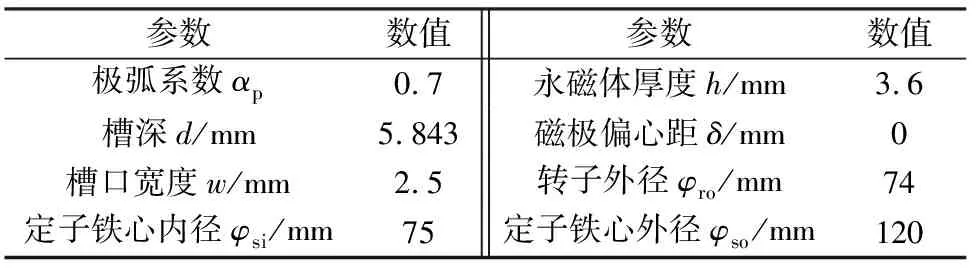
表1 永磁同步電機的初始參數值

結合 ANSYS Maxwell軟件，計算電機內部各初始損耗:鐵耗為12.53 W,銅耗為88 W,永磁體上的渦流損耗為2.1 W,機械損耗為12 W,初始效率為85%。

結合ANSYS Workbench軟件，計算電機噪聲初始值。由于永磁電機的噪聲值主要分布在開關頻率及其倍頻附近，選取頻率范圍為0～10 kHz,測取6 kHz處的電機噪聲值約為51.5 dB( 如圖1所示)，根據新版GB10069.3-2008《旋轉電機噪聲測定方法及限制 第3部分：噪聲限制》的介紹，該規格電機噪聲值應在50 dB左右，因此算例噪聲值符合規定值。其中圖2和圖3分別是電機初始時定子內表面的徑向磁拉力和等效應力。

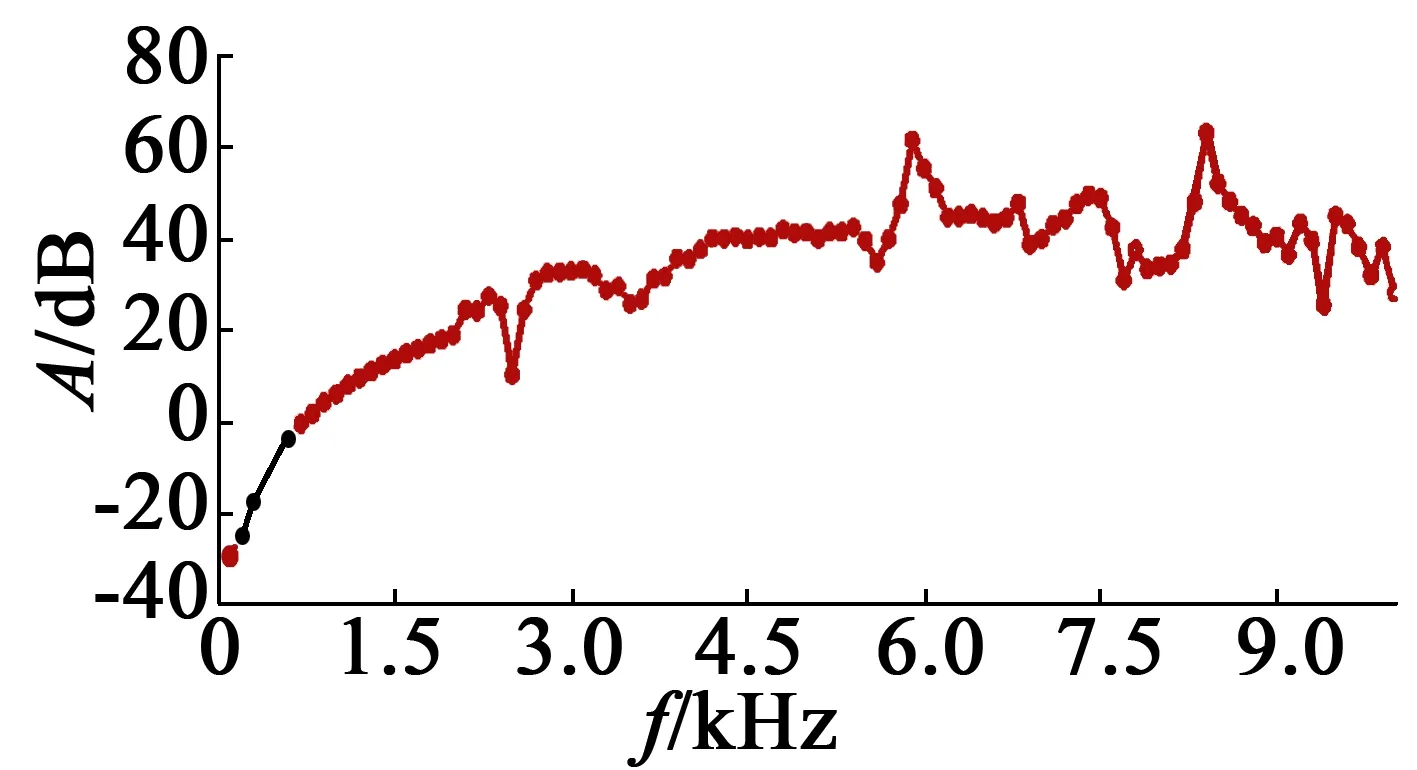
圖1 初始時聲場分析的SPL

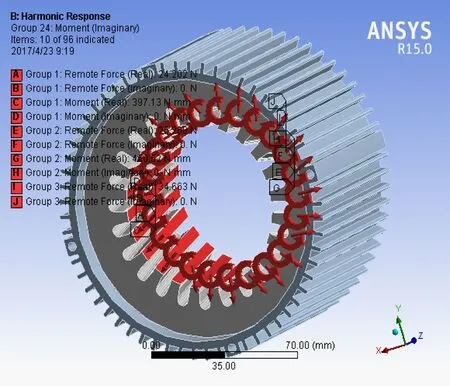
圖2 初始定子內表面的徑向磁拉力

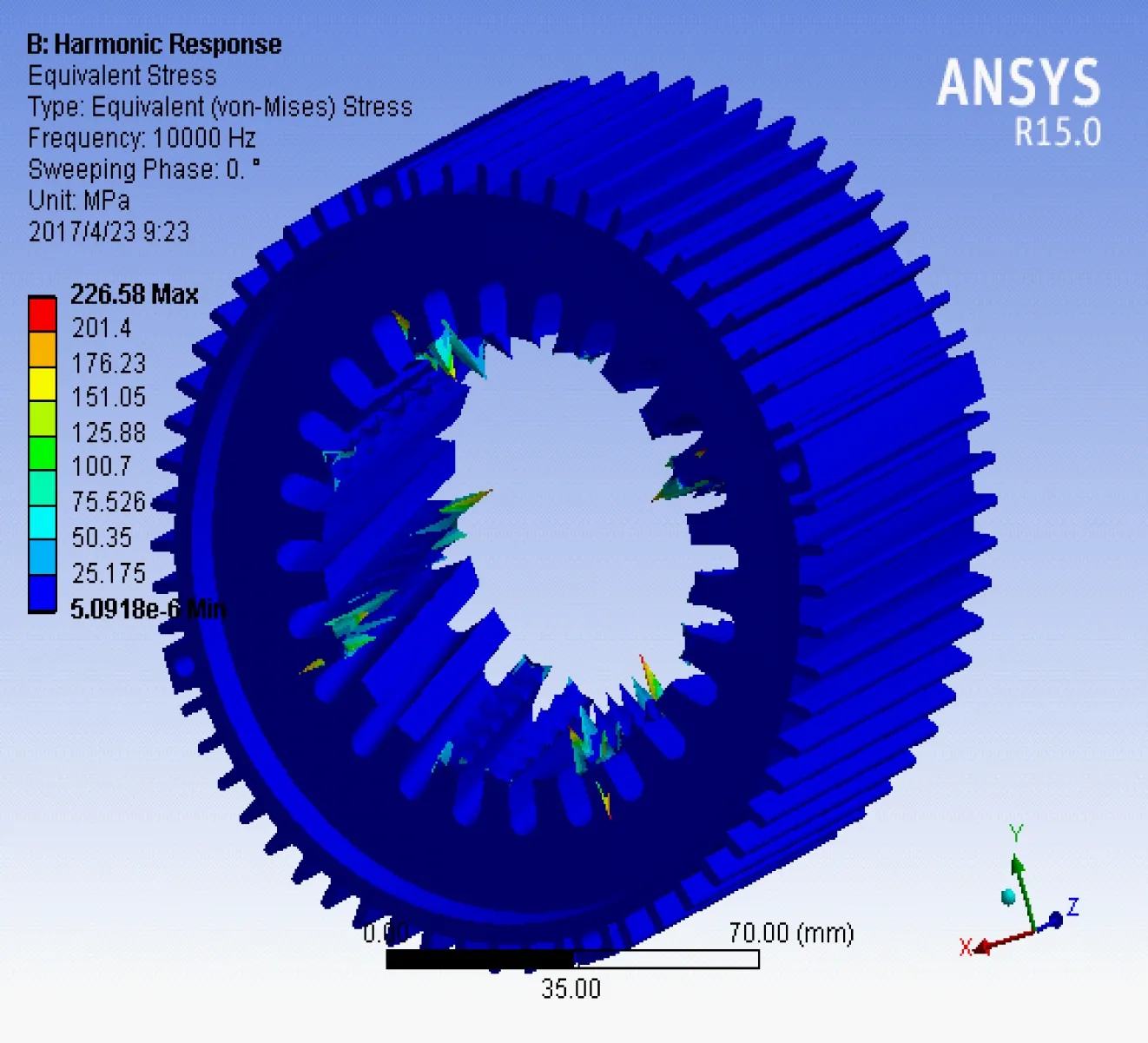
圖3 電機的初始等效應力

3.2 數據樣本的建立

此過程的建立是為后面支持向量機的擬合提供樣本空間。數據樣本由5個設計變量(磁極厚度、極弧系數、槽深、磁極偏心距、槽口寬度)、2個目標函數(效率和噪聲)和1個約束條件(電機轉矩)組成,每個設計變量取5個值,共3 125個數據。為了抽取具有代表性的樣本數據，采用正交試驗法對數據樣本進行收集。

本文中5個因素的取值范圍分別為磁極厚度1.5 ～3.5 mm,極弧系數0.6～0.72,槽深5～8 mm,磁極偏心距1～5 mm,槽口寬度2～4.5 mm。根據因素和水平的個數，選取L25(56)的正交試驗表，各因素所對應的水平如表2所示。

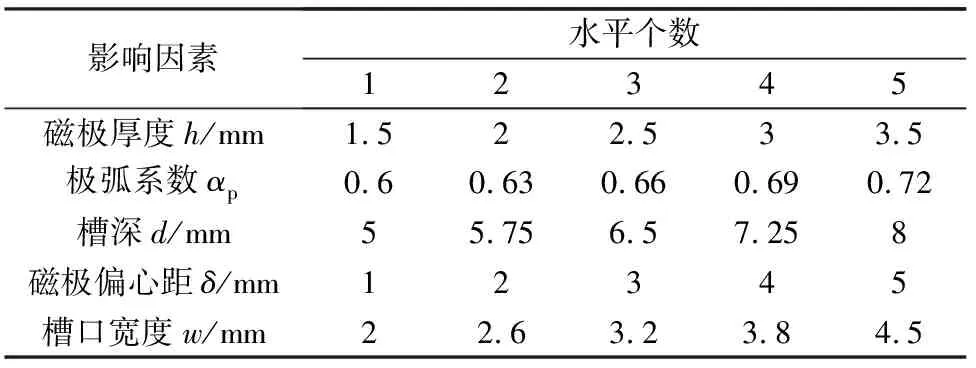
表2 因素水平表

3.3 數學模型的建立

支持向量機(以下簡稱SVM)是一種針對有限數據進行研究的新型學習方法，主要有兩大應用：函數擬合和數據分類。本文主要利用其函數擬合功能，利用高斯徑向基核函數求解約束條件和目標函數的數學模型[7]，為下面粒子群多目標優化奠定基礎。

SVM函數擬合功能的原始方程式：

(1)

式中:n代表SVM的個數,本文為25個；ωi代表SVM的系數，保存在程序結果model.coef里面；K(xi,x)=exp(-γ‖xi-x‖)2,其中‖xi-x‖為二范數距離,xi=model.svs(i,:),表示支持向量(1×5的行向量)，全部向量保存在程序結果的model.svs里面，x是待預測向量(1×5的行向量)；b*是偏置系數。從式(1)中可以看出，欲想得到3個數學模型，需要編寫程序求出高斯徑向基核函數、偏置系數及高斯徑向基核函數的系數。本文采用libsvm工具箱分別把3個數學模型的25組數據作為訓練集，另外取20組不同的數據作為測試集，通過交叉驗證的方法[8],求取3個未知參數。

將程序結果中的model值代入到式(1)中，得到約束條件和兩個目標函數的數學模型，SVM的模型預測數據和真實數據之間的對比如圖4所示。從圖4中可以看出，預測值與真實值變化趨勢基本一致，說明3個數學模型擬合有效。

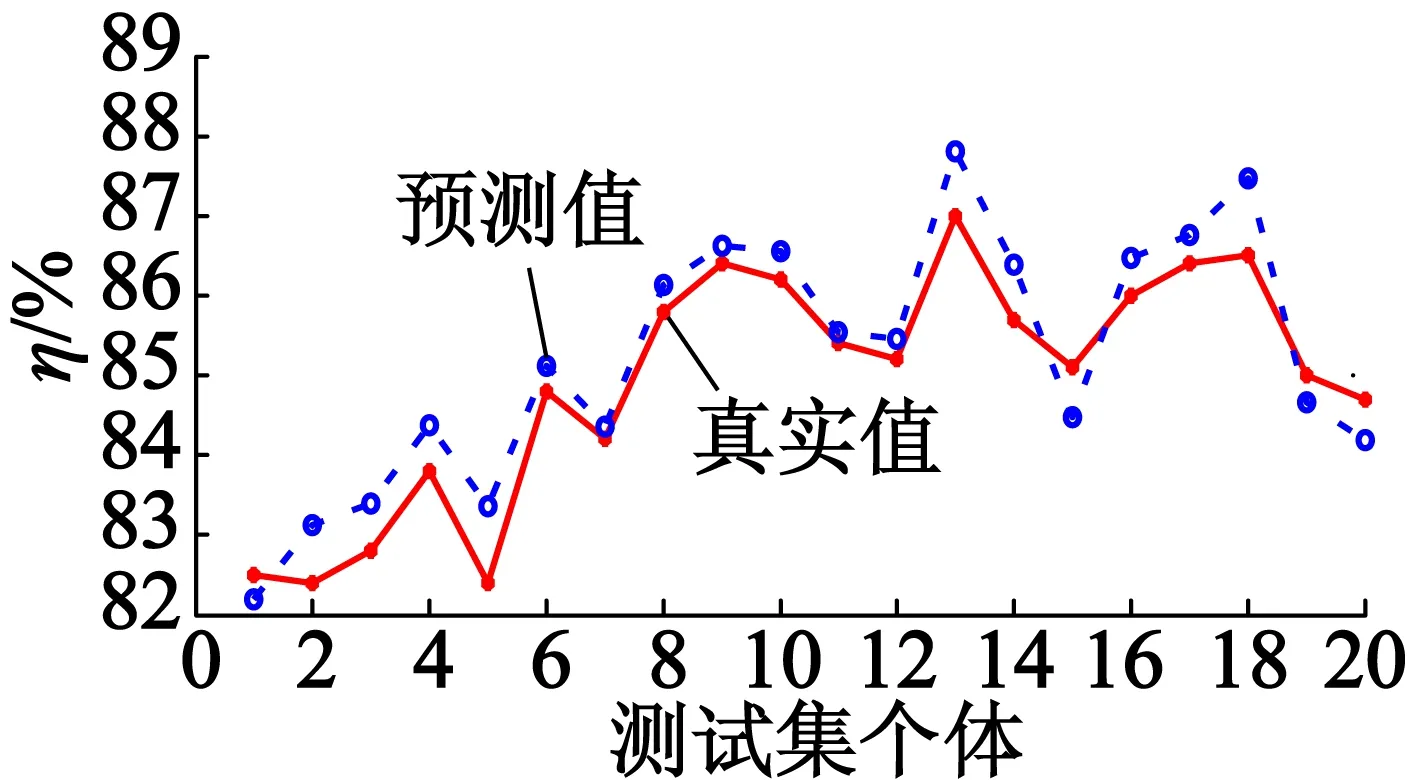
(a) 效率擬合曲線

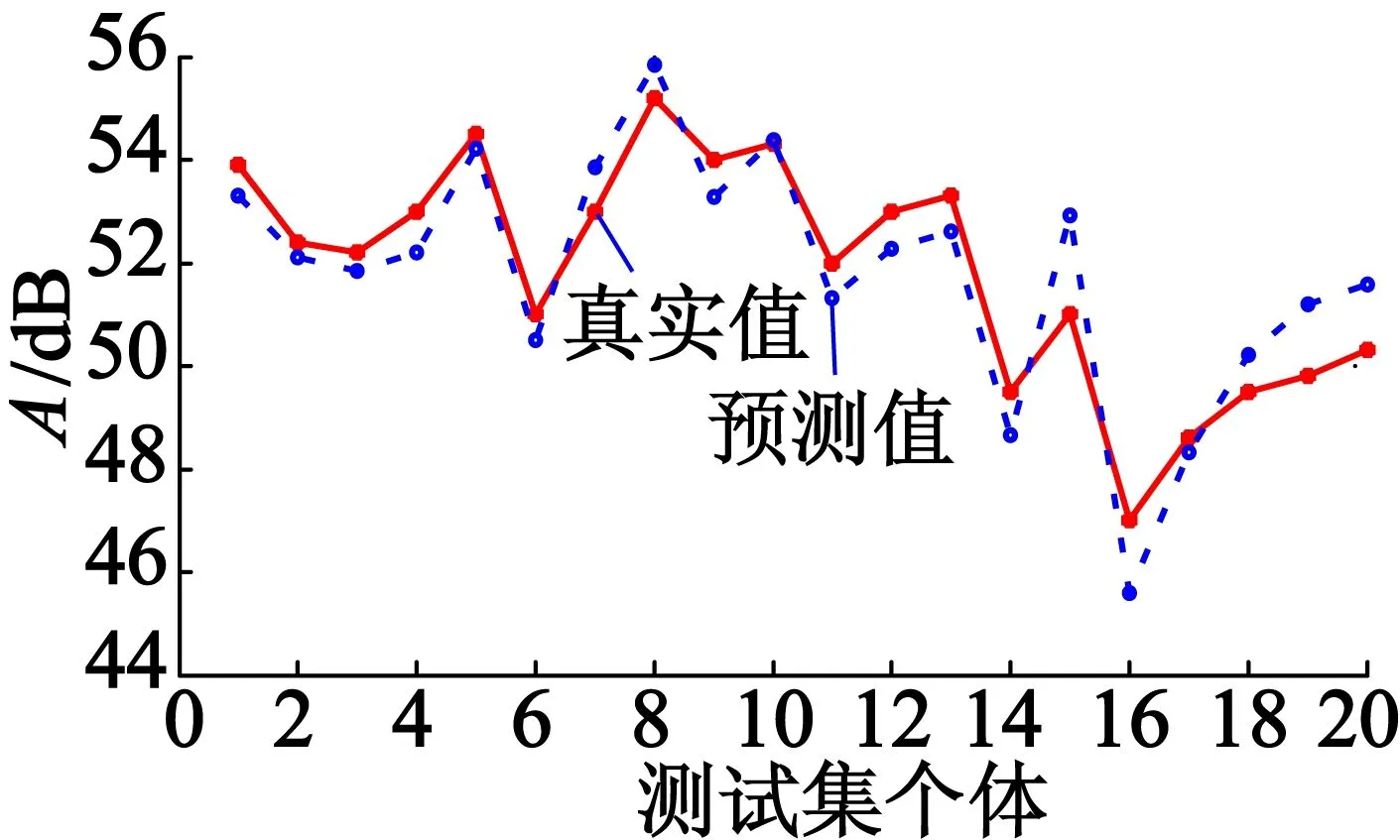
(b) 噪聲擬合曲線

(c) 轉矩擬合曲線

3.4 粒子群多目標優化

在實際工程優化問題中,多數問題是多目標優化問題,本文利用粒子群多目標優化算法,在電機轉矩一定的條件下實現對效率和噪聲的尋優[9-10]。粒子群多目標優化與單目標優化一樣,都需要不斷更新粒子的速度和位置，其速度和位置公式如式(2)、式(3)所示。

(2)

(3)

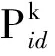
ωk是動態變化的，假設K為迭代總次數，則第k次迭代時的慣性權重：

(4)

式中:ωmax和ωmin分別為迭代前已設置好的最小值和最大值。

式(3)中ωk的值對尋優能力有較大的影響。粒子群尋優算法分為全局搜索和局部搜索，當全局搜索能力較強時，其算法收斂速度較快；當局部搜索能力較強時，其算法收斂精度較高，而較大的ωk值有利于前者，較小的ωk值有利于后者。式(4)中對ωk的處理可以同時兼顧這兩種情況，搜索能力得到加強。優化后的結果如圖5所示，圖5中每個實心點都代表一個非劣解，非劣解構成了Pareto面。從圖5中可以看出，各個非劣解分布較為均勻，并且Pareto面前端形狀良好。

圖5 非劣解空間分布

從圖5中可以看出，優化得到的不是最優解，而是一個非劣解集，需要從非劣解集中根據實際問題選擇需要的解[11]。本文從圖5中選擇,3組形狀良好的Pareto前端進行比較，每組選擇2個點，將6個值代入到軟件中進行計算，與粒子群優化(以下簡稱PSO)尋優的結果進行對比，如表3所示。

綜合考慮后選取(3.5,0.63,5,5,3.8)為實際問題的最優解，此時電機的各種損耗:鐵耗12 W，銅耗60 W，永磁體渦流損耗2.23 W，機械損耗12 W,效率為86.5%，噪聲值為46.5 dB。與初始時的效率和噪聲相比，性能得到改善。噪聲值變化曲線如圖6所示，圖7和圖8分別是優化后電機定子內表面的徑向磁拉力和等效應力。

表3 有限元計算和PSO計算結果對比表

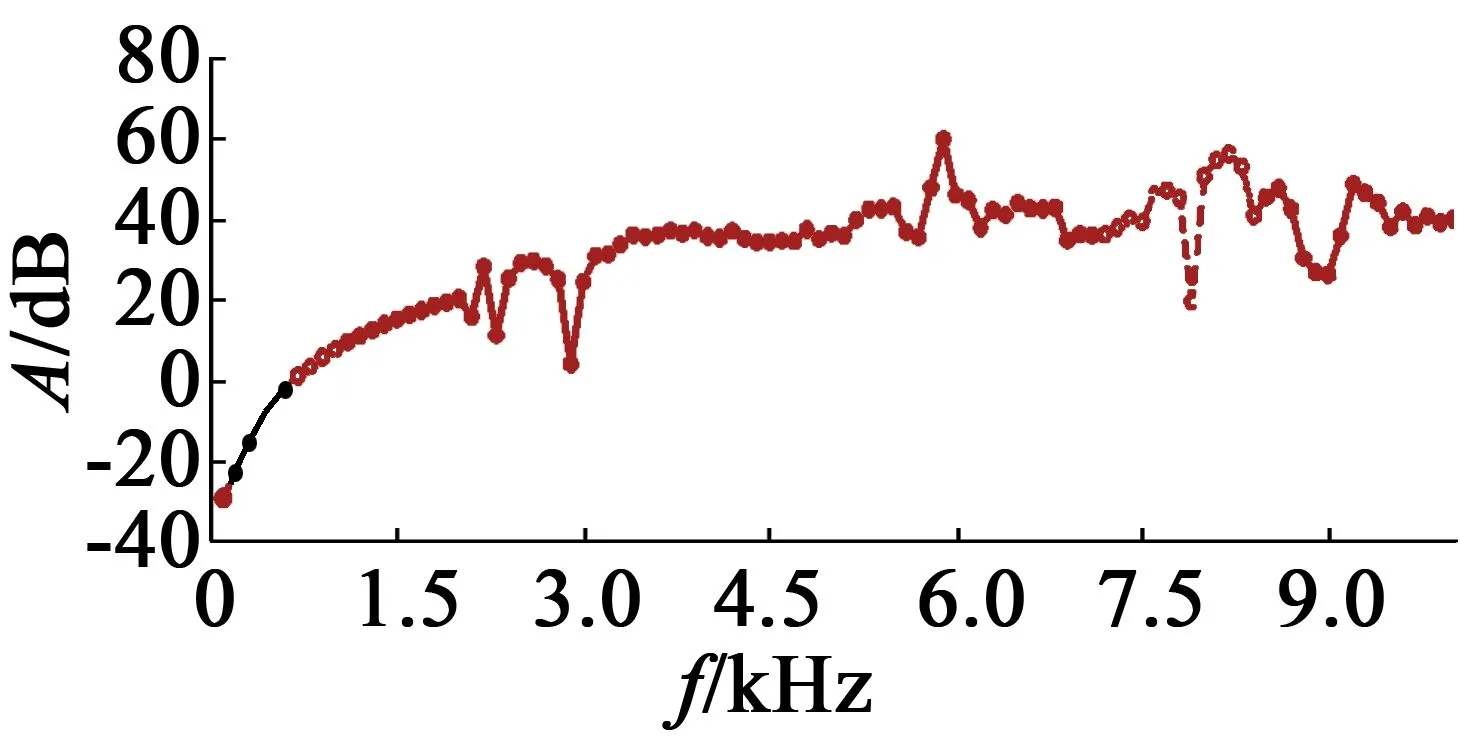
圖6 優化后聲場分析的SPL

圖7 優化后定子內表面的徑向磁拉力

圖8 優化后電機的等效應力

4 結 語

本文從影響永磁同步電機效率和噪聲的主要參數出發，通過利用具有約束條件(保證電機轉矩一定)的粒子群多目標優化算法對電機的效率和噪聲進行優化。

在優化過程中，首先利用正交試驗法為SVM的擬合選取數據樣本，然后利用SVM求解約束條件和兩個目標函數的數學模型，最后在保證電機轉矩足夠的條件下，利用粒子群多目標優化算法對效率和噪聲進行尋優。最后依次將最優解的有限元計算值與PSO優化值以及電機初始值進行對比，發現效率和噪聲均得到改善，說明研究具有一定的實際意義。