基于均一化模型的MFC懸臂梁靜態變形分析

盛賢君，周少征

(大連理工大學 電氣工程學院,遼寧 大連 116023)

0 引言

壓電纖維復合材料致動器由于兼有壓電系數高和柔韌性好的優點已逐漸在機翼變形與振動控制等領域取代了單純材料的壓電致動器[1-2]。為了準確獲取壓電纖維復合材料的宏觀性質，需要對其細觀結構進行研究[3]。粗壓電纖維復合材料(MFC)是一種由鋯鈦酸鉛壓電陶瓷(PZT)纖維、集成電極、環氧樹脂和聚酰亞胺構成的二維周期性壓電纖維復合材料，而均一化技術是根據復合材料的細觀結構分析其宏觀性質的有效方法。為了分析MFC的宏觀性質，DERAEMAEKER A等提出了一種基于平面應力假設和二維周期性位移場假設的MFC均一化模型[4]。在實際應用中，由于MFC與被驅動的結構之間存在力學耦合作用，難以完全且嚴格地滿足上述假設條件。為了研究該均一化模型在實際應用中的精確性，以MFC致動器驅動懸臂梁靜態變形為例，在ANSYS中分析了采用該均一化模型與不采用均一化模型下梁的撓度對比。在該均一化模型中，P1型MFC僅有e32和e33兩個非零的壓電應力常數，為了進一步簡化該模型，提高分析效率，研究了忽略該模型中的e32效應對于分析MFC懸臂梁靜態變形撓度精確性的影響。

1 MFC致動器的結構

由美國蘭利研究中心研發的MFC致動器是一種高效且柔韌的壓電致動器，目前由Smart Material 公司生產和銷售。P1型MFC致動器的結構如圖1所示。

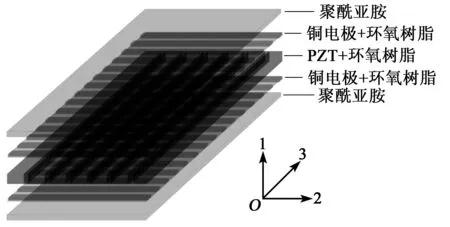
圖1 P1型MFC致動器的結構

其中，聚酰亞胺層為MFC致動器的表皮；銅電極為交替排列的正負電極，中間由環氧樹脂填充；PZT為并列的長方體粗纖維，型號為PZT-5A1，中間由環氧樹脂填充。PZT與銅電極的長度方向相互垂直，各層之間緊密相接。圖1中，MFC致動器各組成部分的幾何、力學和電學參數分別如表1～4所示。

表1 聚酰亞胺的幾何和力學參數

表2 環氧樹脂的力學和電學參數

表3 銅電極的幾何和力學參數

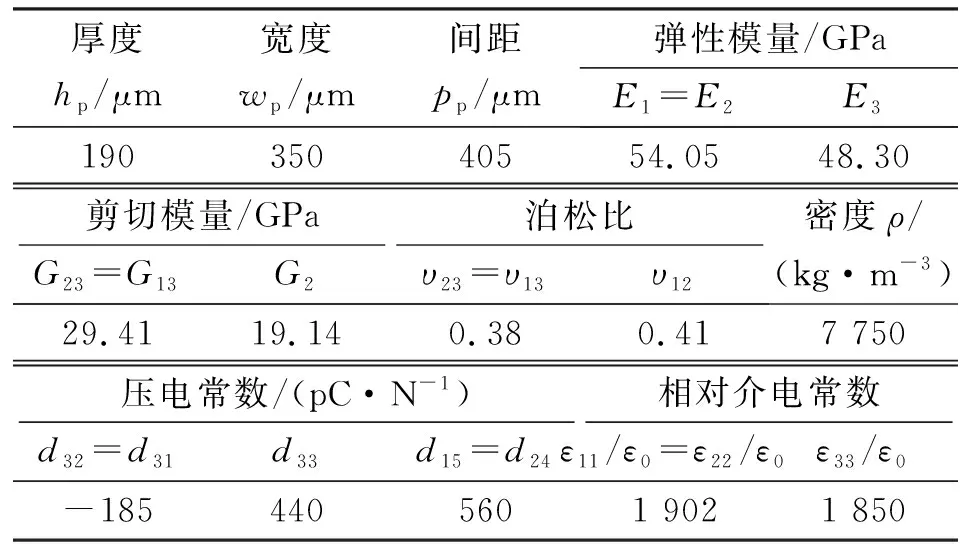
表4 PZT粗纖維的幾何、力學和電學參數

表4中，下標1、2和3表示的方向如圖1所示，超過3的下標按IEEE標準定義。

2 MFC的均一化模型

采用均一化模型分析MFC懸臂梁的靜態變形需要先利用MFC的典型體積單元(RVE)獲得其均一化的宏觀性質參數。P1型MFC的RVE的結構如圖2所示，其均一化模型如圖3所示。

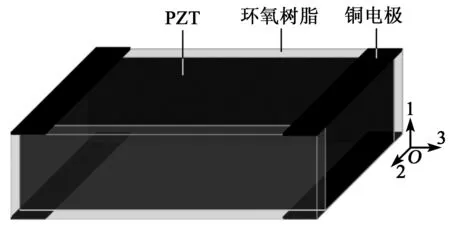
圖2 P1型MFC的RVE的結構

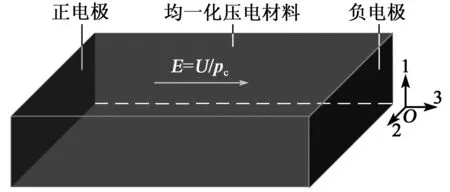
圖3 P1型MFC的均一化模型

圖3中，E為MFC的均一化電場強度大小，U為施加在MFC相鄰銅電極上的電壓大小。采用平面應力假設：MFC在1方向上的正應力(T1)為0，則MFC的均一化壓電方程[4-5]為

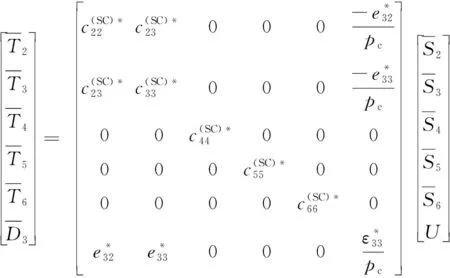
(1)

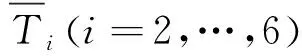
(2)

(3)

(4)

式中：VRVE為RVE的體積；Ti(i=2,…,6)和Si(i=2,…,6)分別為RVE中對應的應力和應變分量；D3為RVE中電位移矢量的方向3分量。

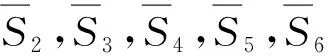
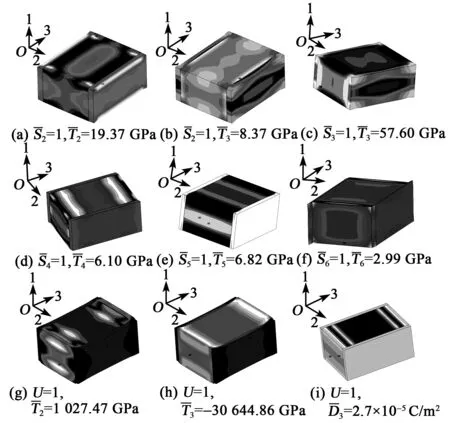
圖4 RVE在6種周期性邊界條件下的應力和電位移矢量

3 MFC懸臂梁靜態變形分析

為了研究基于平面應力假設和二維周期性位移場假設的均一化模型在MFC懸臂梁靜態變形分析中的適用性，在ANSYS中建立了一個利用MFC致動器驅動一個同等面積的厚為1 mm的鋁懸臂梁仿真模型，此MFC致動器在圖1中的2和3方向上分別包含5和20個RVE。仿真中考慮了MFC致動器的聚酰亞胺層和銅電極層，并且MFC致動器與鋁懸臂梁由一層厚為18 μm的環氧樹脂粘接。

MFC的均一化參數是基于平面應力假設的，不同于常規的三維模型參數，因此在使用MFC的均一化模型進行ANSYS仿真時進行了一些特殊的設置，具體包括：

2) 利用結點約束方程使MFC的均一化壓電材料區域的S1為0。

以上設置考慮了MFC的均一化模型中電場只有方向3上的分量和平面應力假設，且能夠保證材料剛度矩陣和介電常數矩陣的正定型。

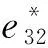
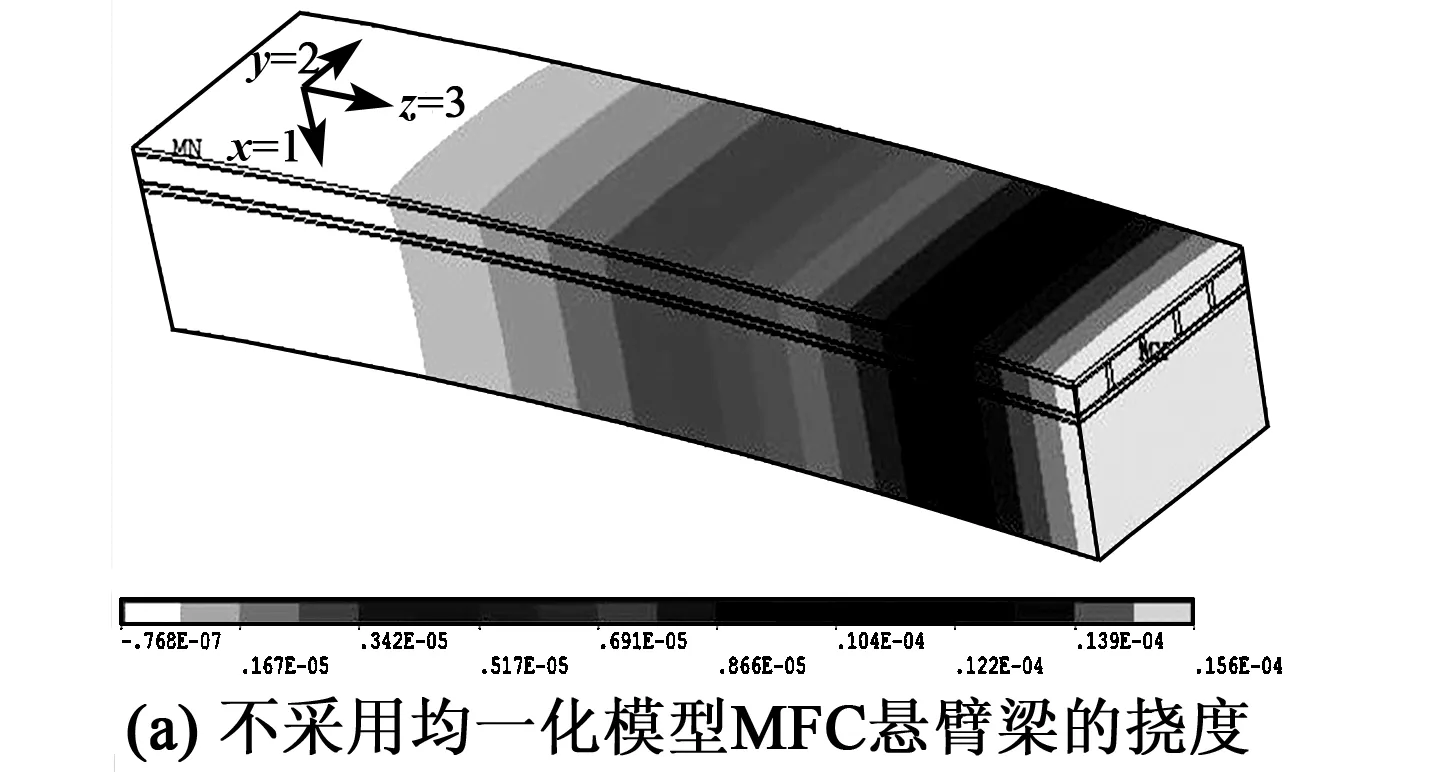
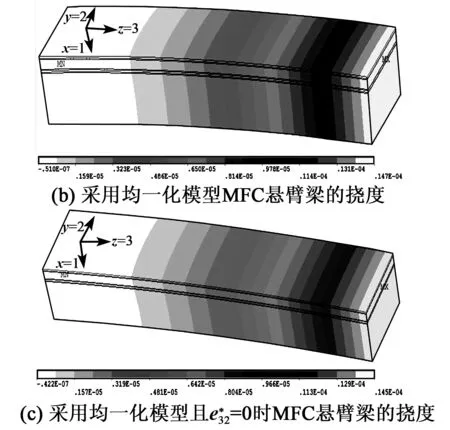
圖5 MFC懸臂梁在3種情況下的撓度

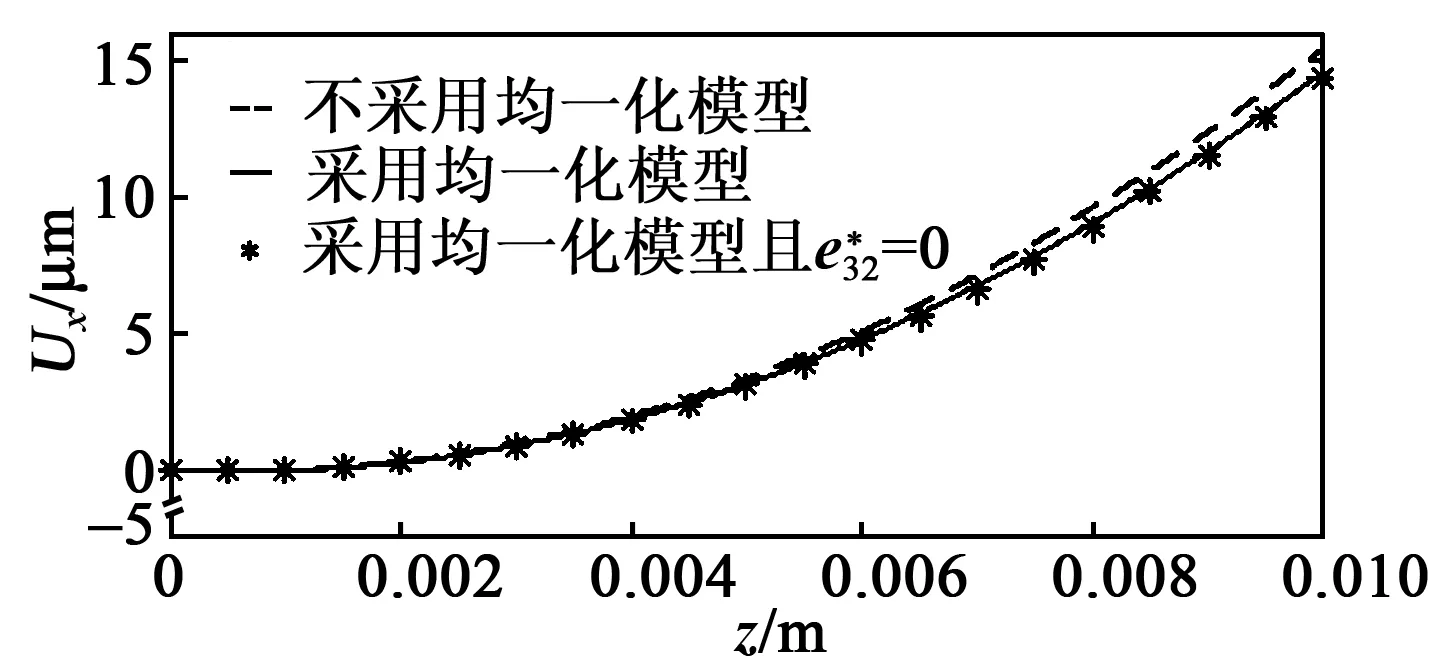
圖6 MFC懸臂梁3種情況下的撓度曲線對比

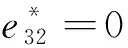
4 結論

采用基于平面應力假設和周期性位移場假設的均一化模型分析了P1型MFC的宏觀性質，給出了計算該均一化模型材料參數的方法和利用該均一化模型進行MFC懸臂梁ANSYS仿真的設置方法。分析了采用該均一化模型、不采用均一化模型及在采用該均一化模型基礎上忽略e32效應3種情況下MFC懸臂梁的撓度。根據以上仿真分析結果可得如下結論：

1) 采用基于平面應力假設和二維周期性位移場假設的均一化模型分析MFC懸臂梁靜態變形是可行的，采用該均一化模型仿真與不采用均一化模型仿真的MFC懸臂梁靜態變形的撓度的相對誤差不超過5.77%。

2) 在精度允許范圍內，使用均一化模型分析P1型MFC懸臂梁靜態變形撓度時可忽略其e32效應，從而進一步簡化模型，提高分析效率。采用均一化模型且忽略其e32效應與采用原均一化模型相比，粱撓度的相對誤差不超過1.36%。