外轉子支點不同心的雙轉子系統振動特性
徐梅鵬, 侯 磊, 2, 李洪亮, 陳予恕
(1.哈爾濱工業大學 航天學院,哈爾濱 150001; 2.哈爾濱工業大學 能源科學與工程學院,哈爾濱 150001)
現代航空發動機多為雙轉子結構,即由內外轉子套裝,通過中介軸承聯接成為一個并聯雙轉子系統。由于在裝配中或機器長期運轉中的熱、疲勞等問題往往難以保證內外轉子的轉軸中心線完全重合,使得系統振動變得復雜,危害航空發動機的安全穩定運行[1],其中主要原因之一是外轉子支承部位發生偏移,造成外轉子支點不同心問題[2]。
雙轉子系統動力學建模常見方法有模態綜合法[3],有限單元法[4-5],傳遞矩陣法[6]等。孫傳宗等[7-9]對復雜結構雙轉子系統的建模和模型簡化方法進行了較為細致的研究,通過對比臨界轉速和振型驗證了簡化方法的有效性。隨著計算機計算速度的發展,有限元軟件仿真方法[10]和數值積分方法[11-12]成為多自由度大模型分析方法的代表。Ferraris等[13]通過有限單元法和實驗雙重手段得到帶機匣的雙轉子系統臨界轉速。Glasgow[14]利用模態綜合法進而計算了雙轉子-軸承系統的臨界轉速和振型。此外,Hou等[15-16]基于改進的諧波平衡法對含強非線性雙轉子系統的近似解析求解方法開展了研究,為雙轉子系統的理論分析提供新的思路。
航空發動機轉子系統易產生多種不對中及不同心形式,并引起學者們關注。Al-Hussain等[17]建立兩跨對稱Jeffcott柔性轉子剛性聯軸器混合不對中模型,分析得到不對中改變了系統的剛度矩陣。Xu等[18-19]根據Hooke鉸的力矩分解,分析得到系統各部分的固有頻率及聯軸器不對中系統的多階偶次倍頻特征,并從實驗上驗證該方法的可行性。李明等[20]建立了具有平行不對中故障的非對稱柔性轉子系統,并探討其非線性動力學行為。張振波等[21]建立多支點柔性轉子系統模型,在不同連接結構下分析得到:支承不同心使得結構剛度呈現非線性且會激起2倍頻分量。Li等[22]通過改進諧波平衡法不對中轉子系統的響應特征。陳果等[23]建立了轉子-滾動軸承-機匣耦合動力學模型,發現不對中和碰摩故障使得高次諧波尤其是偶次諧波成分將顯著增高。對于雙轉子系統,李全坤等[24]建立了雙轉子聯軸器不對中故障模型,研究發現高低壓轉子振動相互耦合,使得2倍頻共振在高低壓轉子上均有體現。馮國全等[25]給出了雙轉子系統支撐軸承不對中的建模分析方法,分析了系統的臨界轉速和響應特征。
本文針對內外軸不重合的故障,建立外轉子支點不同心雙轉子模型,并將不同心影響轉化為支承上附加的等效不同心彎矩,采用二維諧波平衡法求解得到幅頻響應曲線,獲得了由不同心引起的故障共振區,通過分析頻譜和軸心軌跡幾何形狀揭示了不同心故障特征,可為不同心故障診斷提供依據。
1 航空發動機雙轉子簡化模型
為使雙轉子系統簡化模型盡可能反映結構特點,做出以下模型假設:①轉軸簡化為不考慮轉軸的扭轉力及軸向力的影響,僅考慮轉子的橫向彎曲振動的剛性軸; ②考慮具有回轉效應的剛體轉盤,其質量和轉動慣量聚集在質心位置,圓盤的不平衡量始終位于回轉平面;③支承處包含中介軸承均簡化為各向同性線彈性支承。
根據假設建立如圖1所示的簡化模型,轉盤的幾何中心分別為O1和O2;m1,m2,e1,e2,Jp1,Jp2,Jd1,Jd2分別為低、高壓軸上的圓盤質量、偏心距、直徑轉動慣量和極轉動慣量。k1,k2,k3,c1,c2,c3,kb分別為3個支座的剛度和阻尼系數及中介彈簧剛度。ω1和ω2分別為內、外轉軸的轉速。

圖1 雙轉子系統簡化模型示意圖Fig.1 Diagram of simplified model for dual rotor system
取內外轉盤質心橫向位移和偏轉角共8個為自由度組,各能量式為
(1)
(2)
(3)
并利用Lagrange方程式(4)來推導振動方程
(4)
式中:L=T-U為拉格朗日函數;ψ為瑞利耗散函數;F(t)為不平衡力。
2 外轉子支點不同心模型
本文研究的模型如圖2所示,由于外轉子在與基礎連接地方發生偏差,大小為Δ,主要造成外轉子軸線發生傾斜,與內轉子軸心線產生角度為α的偏角。外轉子支點不同心的影響可以等效為外轉子支點處的附加不對中彎矩Fm,從而得到外轉子支點不同心雙轉子系統的振動方程
(5)
式中:X={x1,y1,θx,θy,x2,y2,φx,φy};M,D,K分別為質量陣、阻尼陣和剛度陣;G為反對稱陣。
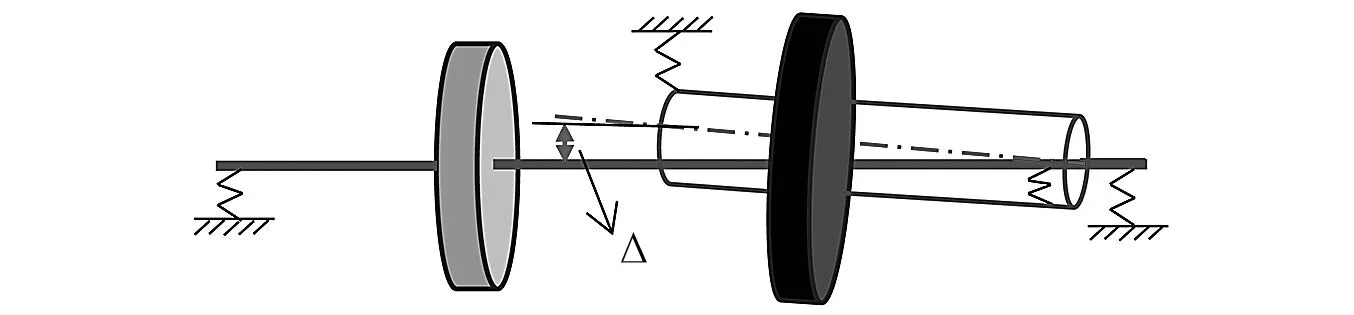
圖2 外轉子支點偏移示意圖Fig.2 Fulcrum-offset schematic diagram
2.1 力矩分解
如圖3所示,假設外轉子的驅動力矩Td水平向左,坐標系o-xyz為固連在外轉子上的坐標系,外轉子的軸心線與z軸重合。將力矩沿z軸分解,有
(6)
根據繞定點轉動的歐拉方程,有
(7)
式中:Iz為外轉子對z軸的主慣量矩。
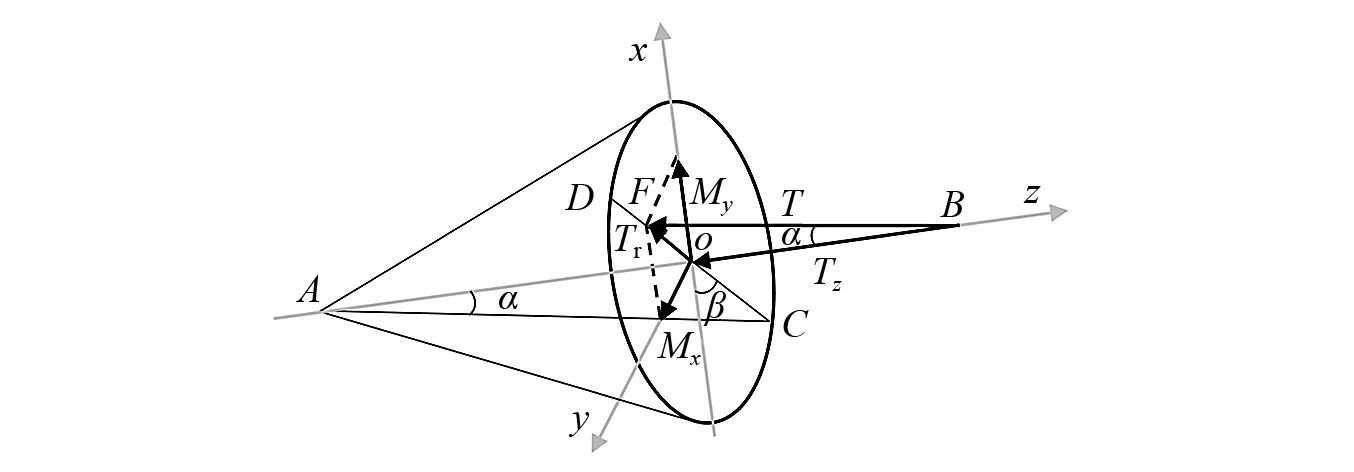
圖3 力矩分解圖Fig.3 Moment decomposition diagram
2.2 帶偏角的角速度傳遞
兩相交轉動軸的角速度比的關系為
(8)
式中:ωd,ωp分別為主從動軸角速度;θd為主動軸轉動角度。
(9)
式中:Δx2, Δy2為外轉子支點橫縱向偏移量。
2.3 諧波分解
(10)
P,Q分別為
(11)
對式(10)左邊項進行諧波分解,得到
(12)
(13)
由θd=ωdt,ωp=ωz, 并將式(12)兩端對時間t微分得到
(14)
式中:B2n=2nA2n,(n=1,2,3,L) 。
在同心的雙轉子系統中,外轉子與驅動軸有著共同的轉動角速度,假設當雙轉子系統出現小角度不同心時,驅動軸的轉動角速度與外轉子轉動角速度保持近似相等ωd≈ω2,進而有
(15)
由外轉子支點不同心轉化的等效不同心彎矩可寫為
Fm=[0, 0, 0, 0, 0, 0,My,Mx]T
(16)
3 二維諧波平衡法
鑒于雙轉子系統受不成比例的ω1和ω2雙頻激勵,需構建二維諧波平衡法。式(5)可以通過以下設解方式來求解。通過引入
τk=ωkt(k=1, 2)
(17)
式中:0≤τk≤2π(k=1, 2)來作為求解的時間尺度則
(18)
(19)
對設解進行諧波分解,有
(20)
式中:aij和bij為諧波項系數,代入動力學方程式(5)有
(21)
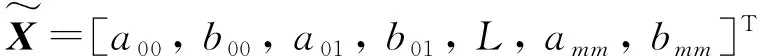
(22)
其中各分塊矩陣為
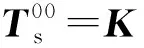
(22)
(24)
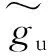
4 研究結果與分析
參數設置:
m1=20 kg,m2=13 kg,Jp1=0.18 kg·m2,Jp2=0.18 kg·m2,Jd1=Jp1/2,Jd2=Jp2/2,e1=1.5×10-6m,e2=1.0×106m,L1=0.275 m,L2=0.36 m,L3=0.165 m,L4=0.105 m,L5=0.05 m,c1=16 N·s/m,c2=16 N·s/m,c3=16 N·s/m,k1=7.5×106N/m,k2=7.5×106N/m,k3=5.0×106N/m,kb=7.5×
106N/m。
4.1 關于諧波平衡法算法可靠性的檢驗
Runge-Kutta法是求解含初值條件微分方程組的強有力工具,具有收斂性好,精確度高等優點,但是求解時間歷程受初值影響大。如圖 4 所示,在不同的不同心角度下,系統的振動響應分別通過HB法和Runge-Kutta法求得,對比發現:當諧波項中m≥6時,兩者的穩態解吻合的較好,但是前者無需多次積分去逼近穩態解,其求解速度更快(兩者求解時間相差兩百多倍),故可取HB法來進行后續求解與分析。

圖4 不同偏角下二維諧波平衡法和Runge-Kutta法的求解對比(-為RK; ·為HB)Fig.4 Comparison between HB and Runge-Kutta under angular variation
4.2 計算結果及分析
雙轉子系統的幅頻曲線出現4個主共振區,同向轉動時,如圖5所示:6 016 r/min,7 162 r/min,10 790 r/min和13 080 r/min(反向轉動時,如圖6所示:6 016 r/min,7 066 r/min,10 310 r/min和11 360 r/min)分屬于外、內轉子自身不平衡力激起的第一、第二階臨界轉速;當雙轉子系統的外轉子支承發生偏移出現支點不同心問題時,幅頻曲線出現新的共振區;由于研究對象是剛性軸,所以研究轉速范圍應低于一階臨界轉速,取低于6 016 r/min的轉速,在偏移角度為0~1.59°時,得到這些共振區的軸心軌跡圖和頻譜圖;當不同心偏角較小時,軸心軌跡在同向轉動時為多橢圓內切圓形(反向轉動時為多橢圓包絡圓形);隨著角度的增大,出現2倍頻率成分并逐漸增大,軸心軌跡形狀出現不同的變化:軌跡移動范圍也變大。當轉速為2 880 r/min時,同向轉動時軸心軌跡出現多橢圓內切圓形→月牙形→剪刀形變化,如圖 7所示(反向轉動時軸心軌跡出現多橢圓包絡圓形→月牙形→剪刀形變化,如圖 8所示);當轉速為5 100 r/min時,同向轉動時軸心軌跡出現多橢圓內切圓形→桃形→“8”字形變化如圖9所示(反向轉動時軸心軌跡出現多橢圓包絡圓形→桃形→內“8”字形變化,如圖10所示)。
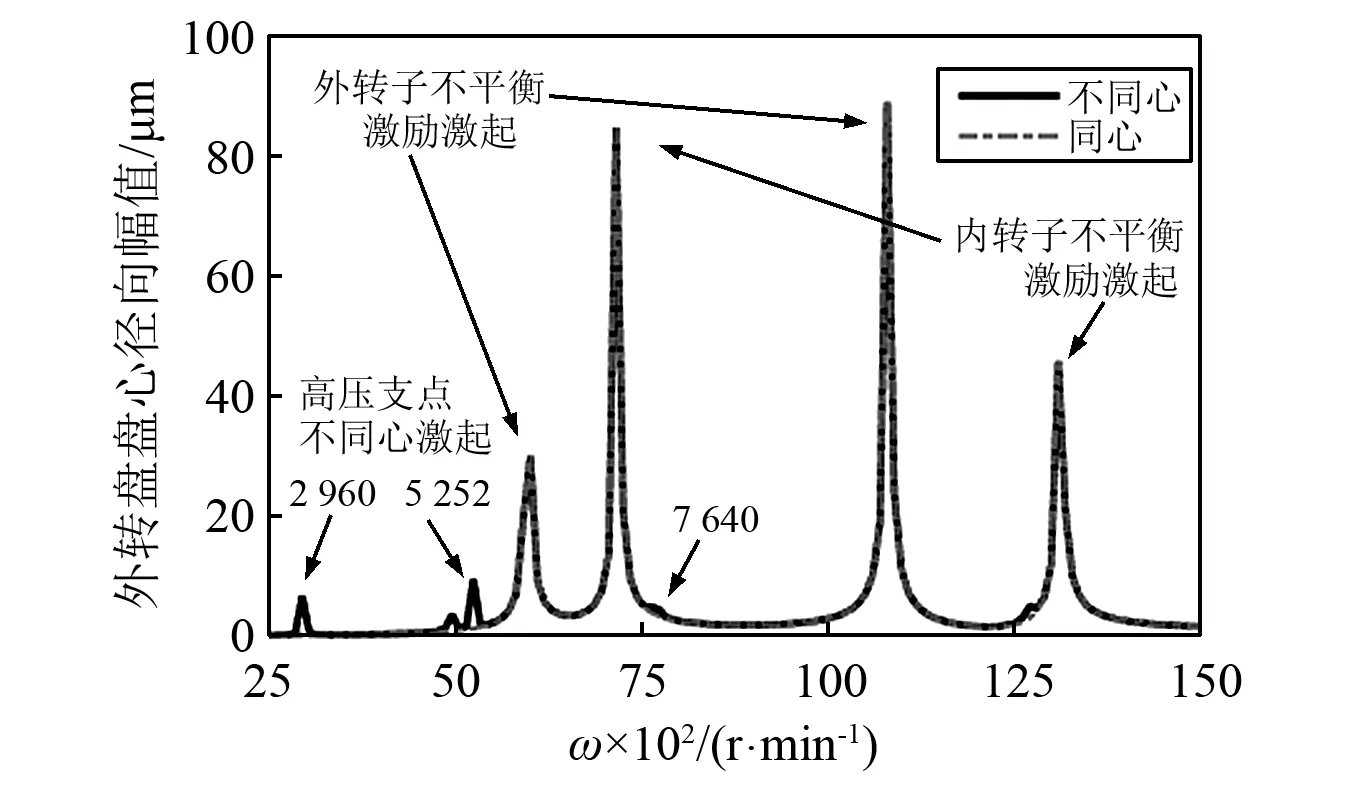
圖5 雙轉子系統同向轉動幅頻響應曲線(α=0, α=1.5°)Fig.5 Frequency-response curves of co-rotational dual-rotor system
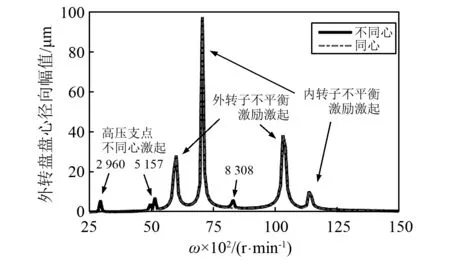
圖6 雙轉子系統反向轉動幅頻響應曲線(α=0, 1.5°)Fig.6 Frequency-response curves of counter-rotational dual-rotor system
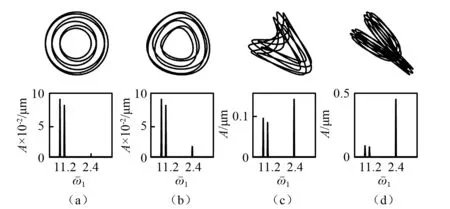
圖7 同向轉動下,轉速ω1=2 880 r/min時外轉子軸心軌跡和x2頻譜隨偏角的變化Fig.7 Outer-rotor orbits and x2 spectrum changing with angle for co-rotation when ω1=2 880 r/min

圖8 反向轉動下,轉速ω1=2 880 r/min時外轉子軸心軌跡和x2頻譜隨偏角的變化Fig.8 Outer-rotor orbits and x2 spectrum changing with angle for counter-rotation when ω1=2 880 r/min
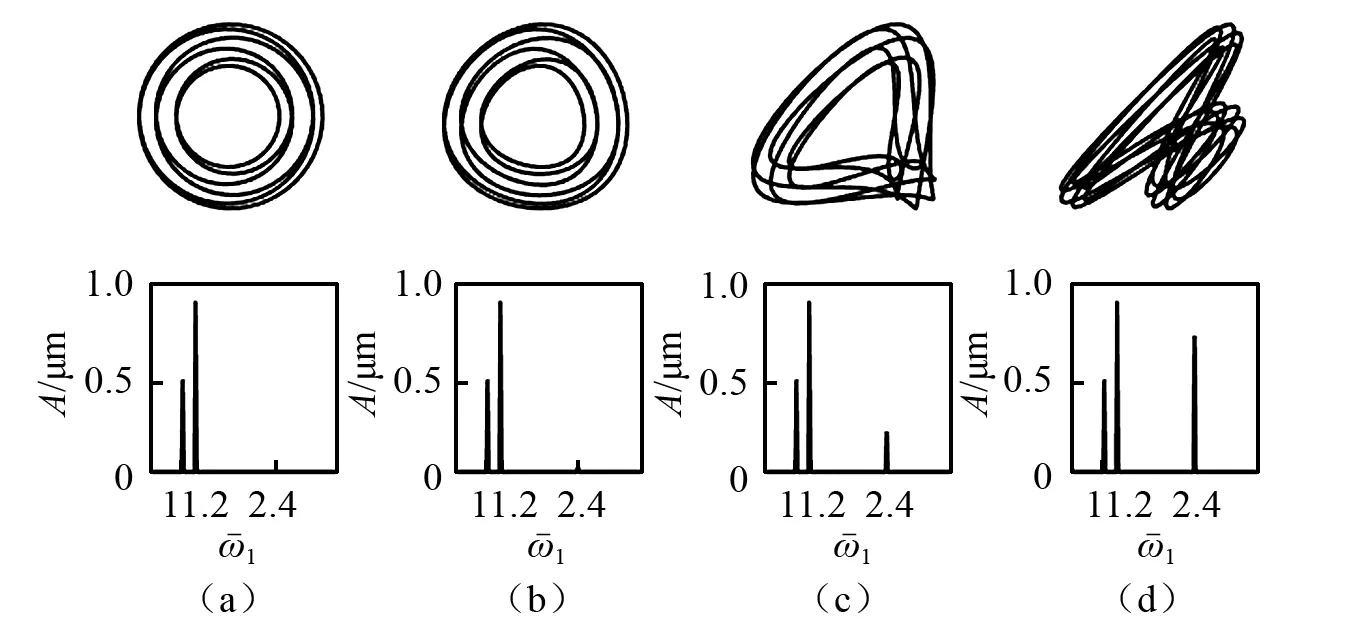
圖9 同向轉動下,轉速ω1=5 100 r/min時外轉子軸心軌跡和x2頻譜隨偏角的變化Fig.9 Outer-rotor orbits and x2 spectrum changing with angle for co-rotation when ω1=5 100 r/min
圖10 反向轉動下,轉速ω1=5 100 r/min時外轉子軸心軌跡和x2頻譜隨偏角的變化Fig.10 Outer-rotor orbits and x2 spectrum changing with angle for counter-rotation when ω1=5 100 r/min
5 結 論
基于質心集中質量法和Lagrange方程建立了外轉子支點不同心的雙轉子系統簡化模型,并通過求解效率高的諧波平衡法求解了系統的振動響應,參數分析可以得出以下結論:
(1) 航空發動機雙轉子系統受雙頻不平衡力激勵,其幅頻響應曲線上出現4個共振區,分別對應由高、低壓轉子自身不平衡力激起的前二階臨界轉速。
(2) 受外轉子支點不同心影響,其幅頻響應曲線出現新的共振區;當不同心偏角較小時,軸心軌跡為多橢圓內切圓形(同向轉動)或多橢圓包絡圓形(反向轉動);其主導頻率成分2倍隨不同心偏角增大,使得軸心軌跡移動并增大而且在不同轉速下,軸心軌跡形狀出現不同的變化形式:在低轉速共振響應區域(小于一階主臨界轉速),軸心軌跡受不同心角度影響,成月牙形,剪刀形或(內)“8”字形,與典型的不對中軸心軌跡特征相似。
本文的研究成果有助于理解不同心雙轉子系統的振動響應特征,從而為不同心故障診斷提供依據。后續將進一步研究考慮支承非線性的不同心雙轉子系統的動力學特性。

