高海拔隧道施工通風風管漏風率研究
李 琦, 于 麗, 嚴 濤, 劉 祥, 王明年
(1. 西南交通大學 土木工程學院,四川 成都 610031; 2. 西南交通大學 交通隧道工程教育部重點實驗室, 四川 成都 610031;3. 中國中鐵二院工程集團有限公司, 四川 成都 610031)
隧道施工中,通常采用管道把新鮮的空氣送到掌子面,把粉塵、有害氣體等排出隧道,以創造必要的作業施工環境,控制漏風量是保證長隧道管道式通風成敗的關鍵。評價和計算通風管路漏風的主要理論有平均百米漏風率理論、高木英夫理論、青函隧道理論和沃洛寧理論等,國內外學者在風管漏風率方面進行了較多研究,其中:Dindorf等[1]研究得到了管道中的空氣泄漏流量要基于在兩個時間間隔中的壓力比測量計算,測量方法在于確定管道中的空氣泄漏流量與受控空氣流量間的關系;Ma等[2]采用實測的方法驗證并得到一種簡化的空氣泄漏測試方法,并證明該方法具有很強的可操作性;趙力等[3]采用試驗的方法對風管的漏率進行研究,最終獲得了簡單可行的風管漏風量及漏風率的計算方法;楊立新[4]針對現有通風管路漏風理論存在的問題,提出通風管路漏風量新的評價指標,通過分析研究推出末段百米漏風率的測定方法,得出了由末段百米漏風率計算漏風量和風機供風量公式;倪文耀[5]基于理想氣體風流連續性方程的近似方法計算礦井外部漏風率所帶來的缺陷,以熱力學基本原理為依據,推導出了測算礦井外部漏風率的正確方法。
高海拔地區主要集中于西部地區,其面積占到我國國土面積的60%以上。為了推動西部經濟跨越式發展,其鐵路交通網不斷在延伸,因而,高海拔隧道的數量和里程也隨之增多。由于隨著海拔高度的提升,大氣環境中出現氣壓降低、空氣密度減小等特點[6]。在高海拔環境中,隧道施工時風管在通風一段距離后便會出現風筒干癟,漏風嚴重的情況,在平原地區情況相對較好,見圖1。高海拔地區由于其特有的氣候特點,即使在風機功率、風壓、風量、風管長度以及破損程度都相同的條件下,風管漏風率在高海拔地區與平原地區也是有差別的。對于高海拔地區隧道的研究目前主要集中在運營通風、制氧供氧、排污衛生等方面[7-12],對于高海拔隧道施工通風風管漏風率的研究還相對比較少。

雀兒山隧道全長7 048 m,洞口海拔高度4 377 m,是目前世界上海拔高度最高的公路隧道。隧址區大氣壓力約為59 kPa,空氣中氧含量約為174 g/m3,兩者均僅為平原地區的60%左右。本文依托雀兒山隧道,對高海拔地區隧道施工通風的風管漏風率進行研究。
1 風管漏風率計算原理
對于通風風管,由于材料和工藝原因,其密閉性存在欠缺,而且在施工過程中,由于一些不可避免的原因造成風管管壁出現破損等情況,導致氣體在風管內輸送時從破損處漏出。原因是當氣體在風管內流動時,流動產生的靜壓將垂直作用于風管管壁,并且氣體的流動會造成風管內外存在靜壓差,因此,如果風管側壁上有孔洞,氣體便會沿著垂直于風管壁的方向從開孔處流出[13]。管道內的風速越大,管道內外的靜壓差越大,則風管的漏風量越大。
靜壓差產生的流速為
( 1 )
風管內產生的流速為
( 2 )
式中:pj為風管內空氣的靜壓差,Pa;pd為風管內空氣的動壓,Pa;ρ為空氣密度,kg/m3。
由于風管內流速的影響,孔口出流方向要發生偏斜,實際流速為合成流速[13],見圖2。

由圖2可知,孔口實際流速為
( 3 )
孔口流出風量為
qv=3 600μfv
( 4 )
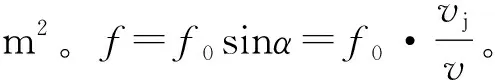
孔口出流風量為
( 5 )
風管的漏風率為
( 6 )
式中:Q為風管內風量。
2 高海拔地區風管漏風率計算
由于風管存在沿程阻力,則風管內各個部位的靜壓有所變化。根據風管漏風率理論以及各個斷面能量守恒公式,可以計算出其各段的漏風率大小,具體計算示意見圖3[13]。
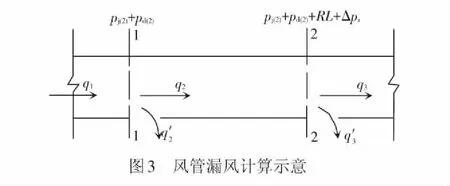
各個斷面能量守恒式為
pj(n)+pd(n)=
pj(n+1)+pd(n+1)+(RL+Δpz)n-(n+1)
( 7 )
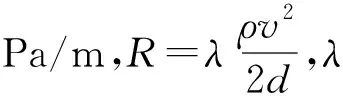

表1 空氣流過側孔直通部分的局部阻力系數
注:表中v1為1-1斷面流速,v2為2-2斷面流速。
由式( 7 )可知,當海拔升高時,空氣密度會減小,則風管中的沿程阻力和動壓減少,由于全壓不變,所以靜壓會增大。由式( 5 )可知,漏風量與靜壓成正比、與空氣密度成反比。因此,在相同條件下,隨著海拔高度的升高,隧道施工的風管漏風率將逐漸增大。
對于風管漏風率計算,可將風管分為n段,每段10 m,分別計算各段的漏風率,在各段風管內可認為風量、風壓、風速不變,根據JTG F60—2009《公路隧道施工技術規范》規定[15],風管的百米漏風率不大于2%,則每段的漏風口面積可近似取為0.008 m2,孔口流量系數μ取為0.63[13],通風風管摩阻系數為0.014,風管直徑d為1.8 m,所用通風機械參數見表2。平原地區空氣密度為1.22 kg/m3,雀兒山隧道海拔4 300 m,空氣密度為0.8 kg/m3。計算得到平原地區和高海拔地區各段風管漏風率見表3、表4。

表2 風機參數
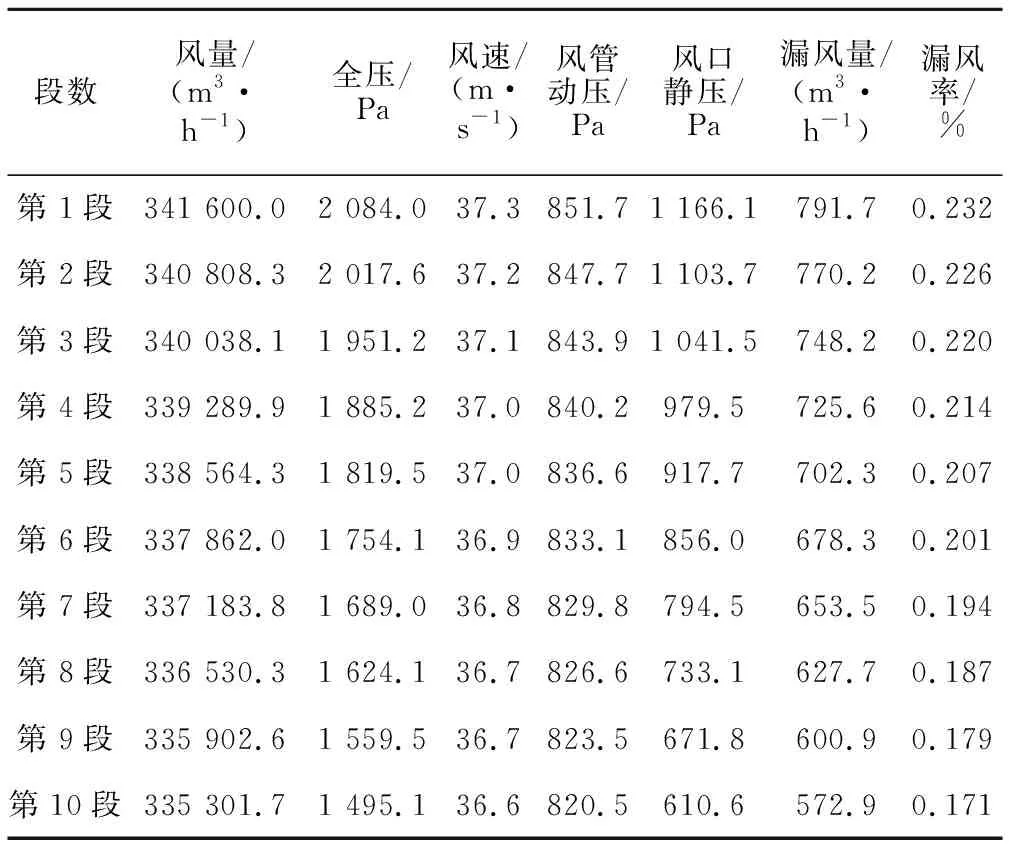
表3 平原地區各段風管漏風率計算結果
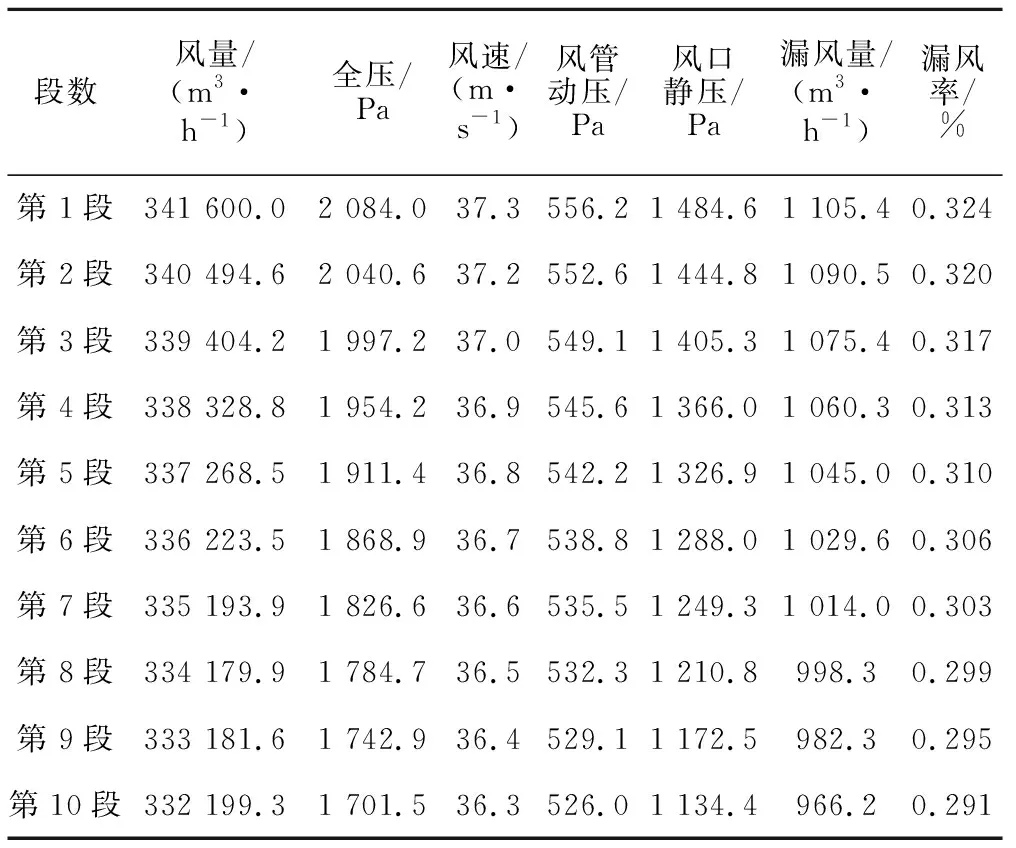
表4 高海拔地區各段風管漏風率計算結果
平原地區和高海拔隧道的風管漏風率曲線變化,見圖4。
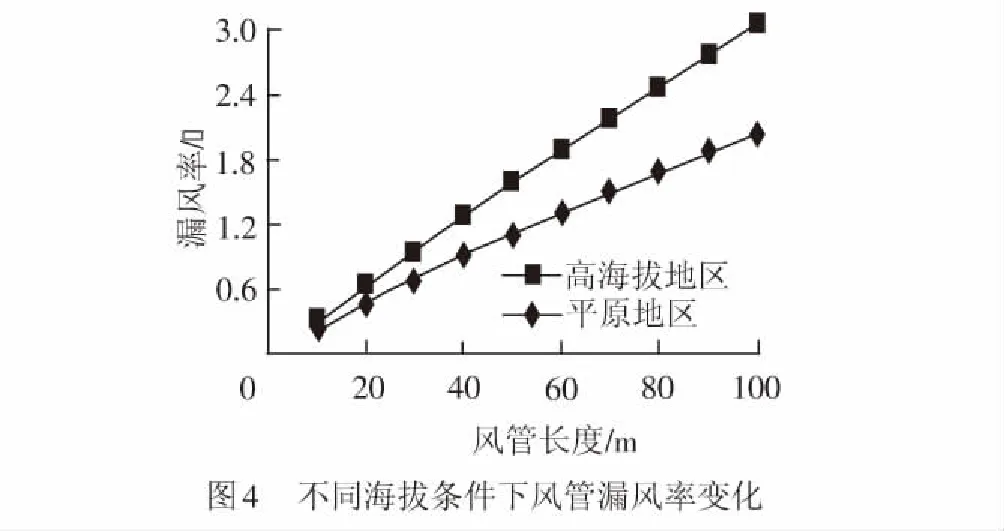
由表3、表4和圖4可知:平原地區的風管百米漏風率約為2.0%,高海拔地區的風管百米漏風率約為3.1%,則高海拔地區的風管百米漏風率約為平原地區的1.5倍,且在高海拔地區風管漏風率隨風管長度增加而增大較快。說明隨著海拔高度的升高,風管的漏風率相應增加,故在高海拔地區更需要對風管進行維修保護,防止漏風率進一步增加。
3 高海拔地區風管漏風率修正
為了得到高海拔地區風管漏風率的修正系數,假設平原地區與高海拔地區風管的破損程度f0和孔口的流量系數μ相同。
則高海拔地區風管漏風率與平原地區風管漏風率相比,可得
( 8 )
式中:c為風管漏風率的海拔高度修正系數。
不同海拔高度的空氣密度見表5,則由式( 7 )可以計算得到海拔高度與風管漏風率修正系數的關系,見圖5。

表5 不同海拔高度的空氣密度
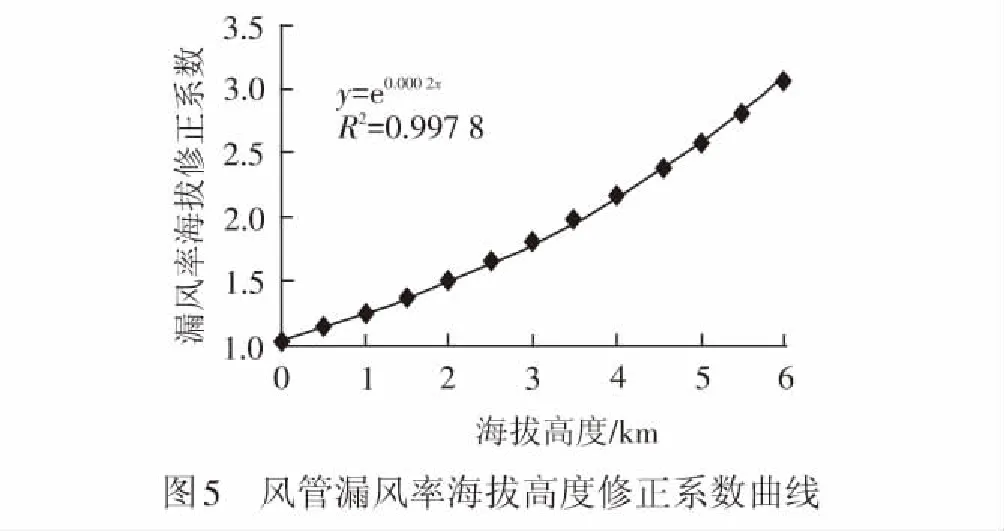
根據高海拔地區風管漏風率修正系數曲線,可以得出高海拔風機漏風率的修正系數理論公式模型為
c=e2×10-4H
( 9 )
式中:H為海拔高度,m。
4 高海拔地區風管漏風率現場實測
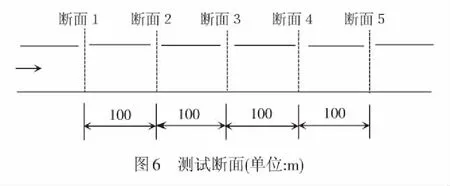
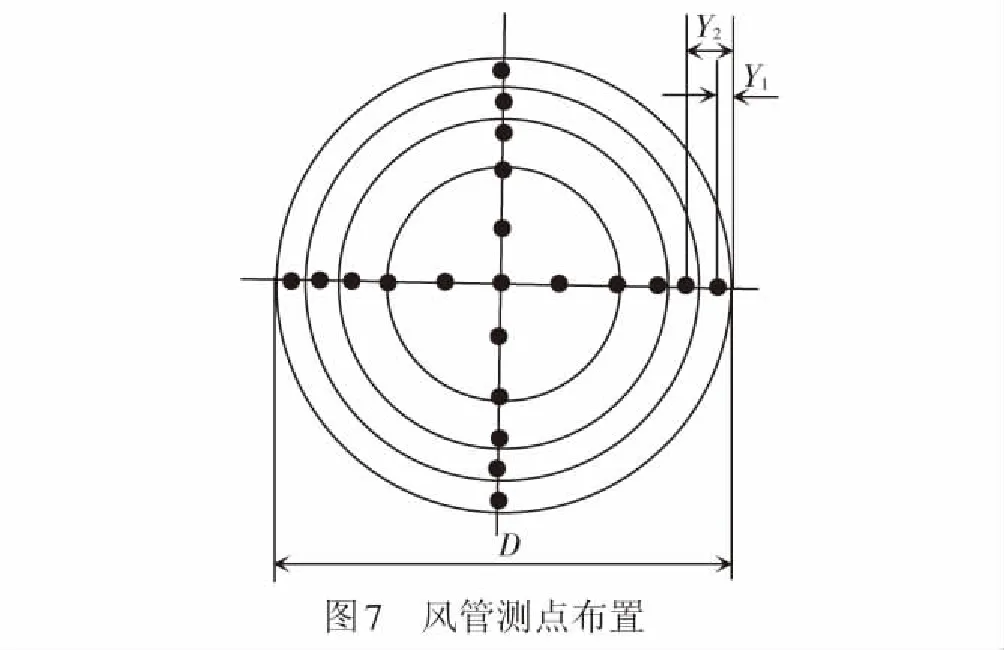
本次測試在海拔4 300 m的雀兒山隧道內,測試段在距風機入口4.5 km附近進行測試,此段風管平直、風流較穩定,每個斷面間距100 m,測試斷面見圖6。所測風機的直徑為1.8 m,由于風管的斷面形狀為圓形對稱,因此,可根據對數線性法確定每個斷面的測點個數為6個,風管橫斷面測點位置見圖7。通過電子風速儀測得每個斷面的6個點位風速值,再取其平均值作為該斷面的斷面風速值。
根據現場測試直線段各個斷面的風速結果進行處理,可以得到風管斷面風速的分布規律見圖8,直線段各個斷面的平均風速見表6。根據理論方法可以計算出400 m直線段的理論漏風率,實測結果和理論結果對比見表7。
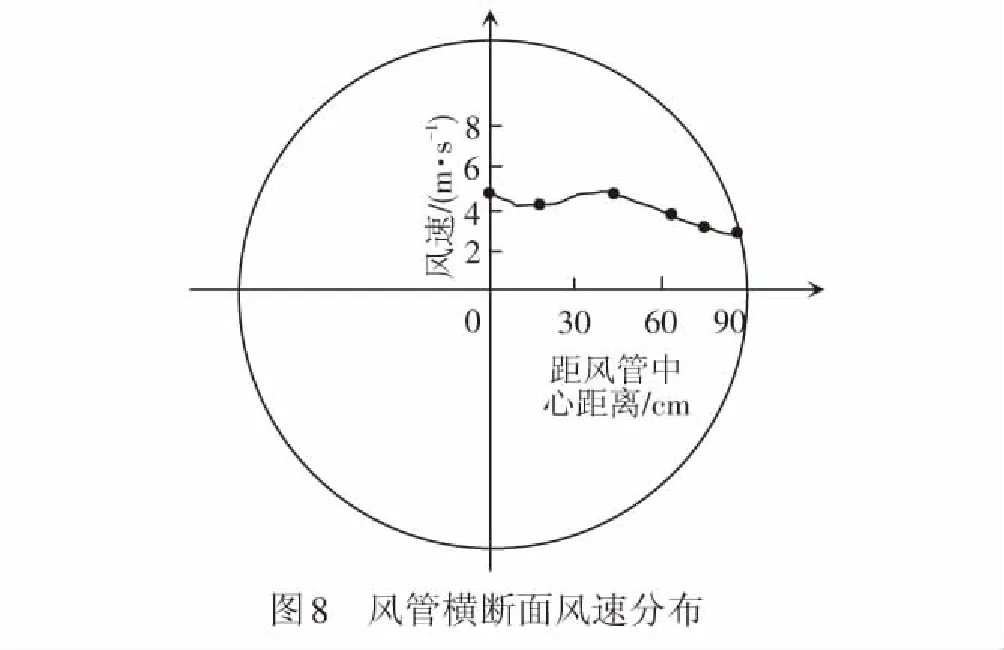
由圖8可知,風管橫斷面上的風速變化規律為風管中心處風速最大,管壁處風速最小,風速整體呈現隨遠離風管中心逐漸減少的分布規律。
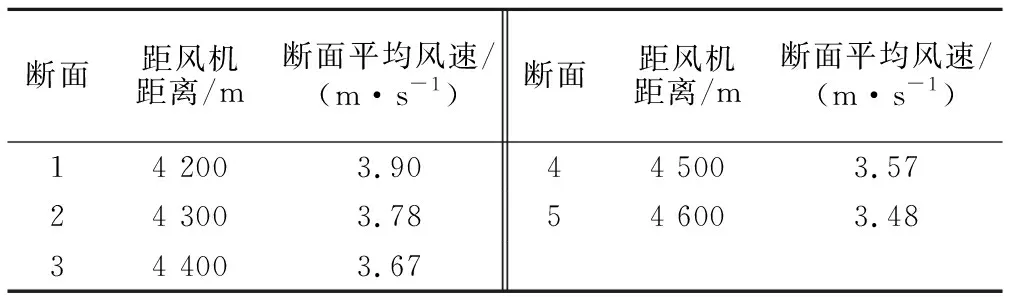
表6 雀兒山隧道風管直線段各個斷面風速測試結果
根據表7計算所得理論上的漏風率可以發現,理論上計算得到的風管漏風率與實際測試得到的漏風率基本相符,約為3%。因此,高海拔隧道施工通風風管漏風率的修正理論公式可靠性得以驗證。
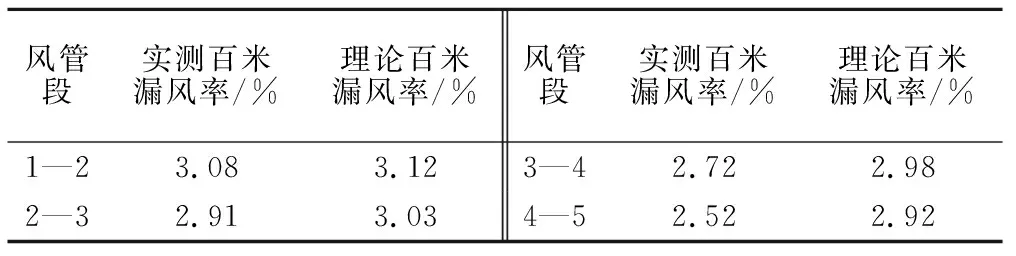
表7 雀兒山隧道風管百米漏風率對比
5 結論
通過對高海拔隧道施工通風風管漏風率的研究,得到如下結論:
(1) 基于風管孔口流量理論,推導得到了風管漏風率的海拔修正系數計算公式。
(2) 通過平原地區和高海拔地區隧道施工風管漏風率的比較,得出高海拔地區隧道施工風管漏風率約為平原地區的1.5倍,且在高海拔地區風管漏風率隨風管長度增加而增大較快。
(3) 實測雀兒山隧道風機風管百米漏風率約為3%,與理論計算結果較吻合。

