小議用合理的情境實現數學抽象教學

馬衛華

(江蘇省南通市通州區金沙中學 226300)

一、生活情境的重要性

生活情境是數學教學使用頻率最高的一種情境，也是數學生活化最貼切的展現．以函數概念教學為例，函數概念教學是中學數學高度抽象、概況的重要概念，影響學生是否能對函數學習掌握得扎實．

案例1 《函數》概念

給出兩段視頻展示(視頻略)：其一，木頭用機器加工成木凳、木桌、木床、柜子等等一系列木制品；其二，面粉用機器加工成包子、饅頭、面條、面餅等．請學生思考，給出的兩段視頻的共性．

生：一段視頻是用木頭加工各種木制品，一段視頻是用面粉加工各種食品．

師：那請把問題抽象一下，你能獲得什么思考？

生：我感覺都是用一種物質加工成各種材料．

師：的確如此，那恰恰想告訴我們，如何從生活的情境中去抽象物理屬性，獲得數學本質呢？讓我們將木頭和面粉一起看成是自變量x，經過一個機器加工獲得了不同的加工品，我們不妨將其看成是y．你能不能用這樣的視頻情境來回顧下初中數學給予的函數概念？

生：就是每一個自變量x經過變化總能得到一個因變量y，這樣的對應關系就是一種函數關系．

生：原來這就是高中函數概念，一點也不難懂．

說明：函數概念是極具抽象的數學概念，其形成的過程歷經數百年．對于如此抽象的函數概念，以往我們不可能僅僅通過數十分鐘的教學就能到位，需要從多個角度去感性的認識，進而獲得數學抽象的形成，可以這么說類似的加工情境很好地展示了函數變化的過程，體現了變量的思想，實現了數學抽象的形成．

二、特殊情境的簡捷性

特殊情境，也是特殊化思想的一種體現．如何利用特殊的數學情境解決問題呢？筆者始終認為，存在即是合理，特別是對于并不追求過程的小題，我們可以創設特殊情境來解決數學抽象的問題．

案例2 抽象函數定義域的求解

抽象函數定義域的求解是難點，學生對這里自變量實在是分不清楚，如：函數f(2x-1)的定義域是指哪個量？函數f(3x+1)的定義域是x∈]1,2]，怎么求f(3x-1)的定義域？的確對于初學者來說，有些分辨不清．我們不妨創設特殊情境，實現數學抽象問題的教學．

問題：(1)函數y=f(x+1)的定義域是(-∞,1]∪]2,+∞)，求函數y=f(x)的定義域．

(2)函數y=f(x)的定義域為(-,1]∪]2,+)，求函數f(x-1)的定義域．

(3)函數y=f(x)滿足f(a+x)=f(b-x)，則函數y=f(x)的圖象關于____對稱．

(4)函數y=f(x)滿足f(a+x)+f(a-x)=2b，則函數y=f(x)的圖象關于____對稱．

分析上述四個小問題，是筆者在抽象函數學習中給學生提出的．學生在學習過程中對于抽象函數的求解陷入了困境，如何理解抽象函數中的定義域？對稱性？在解析式缺失的情況下，如何利用已經掌握的數學知識？這都成了學習的難點．因此，對于初學者來說，我們暫時回避抽象問題的解決過程，而是利用特殊情境的手段換元題目，讓其形態具體展示出來．筆者請學生開發問題(1)和問題(2)的具體特征形態，如下表：

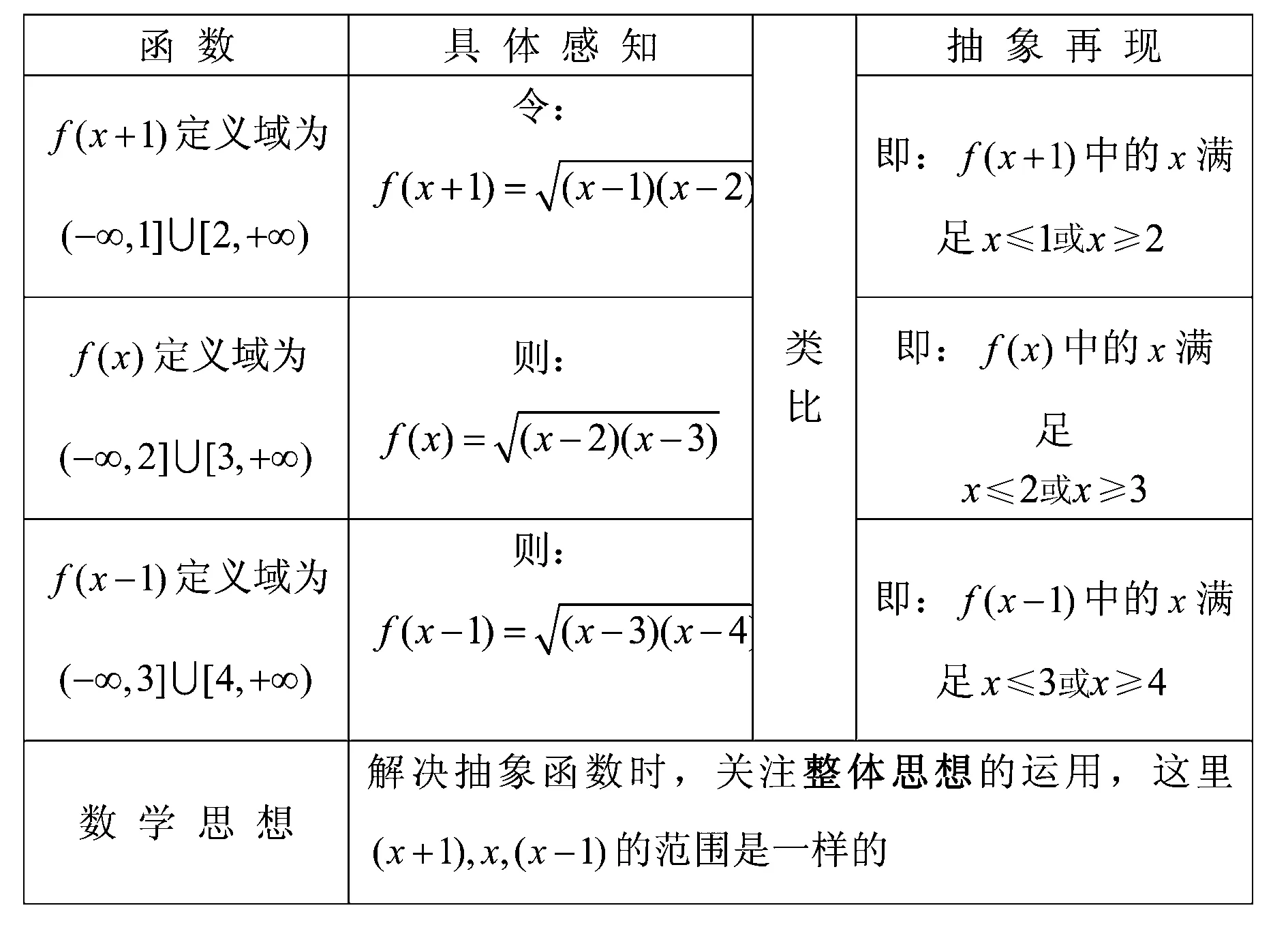
問題(3)和問題(4)，如下表：

顯然，任何一個抽象定義域指的都是自變量x的取值范圍，如函數y=f(x+2)的定義域所求的是“x”的范圍，而不是“x+2”的范圍；其次在解決問題過程中，法則f作用的部分，要關注其整體，即對于法則“f”來說，勢必要關注其針對的整體，即法則“f”下兩個整體部分的范圍的一致性，如“函數x=f(x+1)”和“ 函數f(x-1)”中，“x+1”和“x-1”的取值范圍是一致的．

總之，能幫助理解數學知識、抓住數學本質的都是數學情境，只要合理利用、善于設計都是我們教學的好手段，有助于我們實現數學抽象的教學過程，加快數學抽象素養的培養．