N摻雜LaAlO3電子結構的第一性原理研究

李 強，譚興毅

(1.湖北民族大學新材料與機電工程學院，恩施 445000;2.湖北民族大學新材料成型及裝備技術產學研中心，恩施 445000)

1 引 言

鈣鈦礦結構氧化物(ABO3)具有豐富的物理和化學性質，廣泛應用于人類的生產、生活中，其命名源于礦物質鈣鈦礦(CaTiO3)[1]。理想的ABO3屬于立方晶系，空間群為Pm3m(No.221)，單胞中原子的分數坐標為：A (0,0,0)，B (1/2,1/2,1/2)，O (1/2,1/2,0)。一般而言，A位是半徑較大的稀土或堿土元素離子，其化學價可以是+1，+2，+3價；相應的B位為半徑較小的過渡元素離子，其化學價為+5，+4，+3價；而O離子價態固定為-2價；并且要組成ABO3型鈣鈦礦結構，離子A，B，O的半徑應滿足緊密堆積原則，即[1]:

式中RA,RB和RO分別為A, B和O離子的半徑，t為容忍因子。一般情況下，t介于0.86～1.03之間可組成鈣鈦礦結構，當t=1時，體系為理想鈣鈦礦結構。常見的鈣鈦礦氧化物材料有KNbO3、BaTiO3、LaAlO3等。

另一方面，近年來，2p輕元素摻雜氧化物產生了鐵磁性，由于其磁性起源不同于傳統的鐵磁性材料而成為凝聚態物理領域研究熱點[2-9]。科學家們對C、N、B等輕元素摻雜二元氧化物ZnO進行了大量研究。Pan等[2]制備了C摻雜ZnO薄膜，發現該薄膜具有室溫鐵磁性，理論計算表明磁性起源于鋅原子與碳原子之間的電子交換。Xu等[10]研究發現B元素摻雜ZnO體系同樣具有室溫鐵磁性，但是將磁性歸結為B和Zn最鄰近的O原子的p電子。Shen等[11]研究了N摻雜ZnO的磁性，將其歸結為N原子p電子和O原子p電子間的p-p耦合。Yang等[6]將研究擴展到了具有鈣鈦礦結構的三元氧化物，并將其磁性歸結為摻雜N原子之間的耦合作用。隨后，本課題組[12-14]研究發現C和B原子間隙摻雜BaTiO3的磁性源于Ti原子未配對的3d電子自旋極化；C原子替位摻雜BaTiO3的磁性源于C原子未配對的2p電子自旋極化，N原子替位摻雜BaTiO3磁性源于N原子的2p電子與O原子的2p電子的p-p耦合作用，B原子替位摻雜BaTiO3的磁性機制可歸結為B原子2p和O原子2p與Ti原子3d電子的p-d耦合作用。本課題組[15]也對另一種鈣鈦礦氧化物KNbO3的空位磁性進行了研究，發現Nb空位和K空位均有磁性，且磁性起源于O原子的2p電子極化。但是在LaAlO3中，其B位的Al原子的電子組態為3s23p1，沒有d電子，2p輕元素摻雜是否可以產生鐵磁性？若存在鐵磁性，其磁性起源機制是什么？這些都值得探究。基于此，本文采用第一性原理計算N摻雜LaAlO3電子結構，發現N替代LaAlO3中的O原子和位于LaAlO3晶胞間隙均產生鐵磁性，其磁性都源于雜質N原子的2p電子與體系價帶頂O原子的2p電子間的p-p耦合。

2 理論模型與計算方法

本文計算工作采用VASP軟件包[16]完成。計算選取立方相LaAlO3為原胞，然后構建2×2×2的超晶胞作為基本計算模型，如圖1(a)所示；本文主要研究了N原子替位、間隙摻雜模型，即N原子替代超胞中的一個O原子和處于超胞的間隙中，分別標記為Nsub-LaAlO3和Nins-LaAlO3，如圖1(b)和1(c)所示。首先對構建的計算模型進行了幾何結構優化。參與計算的價態電子為：N 2s22p3, La 5d16s2, Al 3s23p1, O 2s22p4。電子與離子實之間的相互作用勢采用基于廣義梯度近似(GGA)的超軟贗勢(ultra-soft)[17]和PBE交換關聯函數[18]。作用在單個原子上的力小于0.1 eV/?，平面波截斷能量取400 eV。

圖1 N摻雜LaAlO3的幾何結構 (a)LaAlO3;(b)Nsub-LaAlO3;(c)Nins-LaAlO3 Fig.1 Geometry structure of N-doped LaAlO3 (a)LaAlO3；(b)Nsub-LaAlO3;(c)Nins-LaAlO3

3 結果與討論

3.1 穩定性分析

生成焓和結合能是判定物質穩定性的重要參數[19-20]，生成焓ΔHf定義為：

ΔHf(LaAlO3)=[Et(LaAlO3)-nLaEbulk(La)-nAlEbulk(Al)-3nOE(O2)/2-nNE(N2)/2]/n

(1)

式中Et(LaAlO3)為摻雜體系的總能量，Ebulk(La) 為穩定La單質的總能量，Ebulk(Al)為穩定Al單質的總能量，E(O2)為一個氧氣分子的總能量，E(N2)為一個氮氣分子的總能量，nLa、nAl、nO、nN分別為超胞中所含的La、Al、O、N原子個數。計算的生成焓數值如表1所示，發現Nsub-LaAlO3，Nins-LaAlO3體系的生成焓小于零，說明N摻雜LaAlO3體系的結構穩定；而且發現ΔHf(LaAlO3)<ΔHf(Nsub-LaAlO3)<ΔHf(Nins-LaAlO3)<0，說明體系結構穩定性按LaAlO3，Nsub-LaAlO3，Nins-LaAlO3的順序依次降低。

體系的結合能的定義為[21]:

Eb(LaAlO3)=[Et(LaAlO3)-nLaEisolate(La)-nAlEisolate(Al)-nOEisolate(O)-nNEisolate(N)]/n

(2)

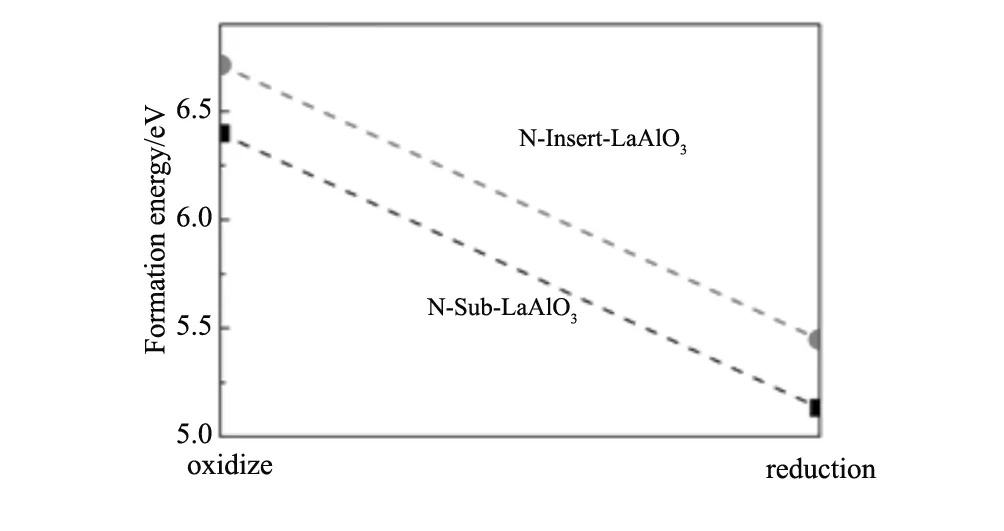
式中Et(LaAlO3)為摻雜體系的總能量，Eisolate(La)為一個La原子的總能量、Eisolate(Al)為一個Al原子的總能量，Eisolate(O)、Eisolate(N)分別為一個O、N原子的總能量，nLa、nAl、nO、nN分別為超胞中所含的La、Al、O、N原子個數。計算的體系結合能數值如表1所示，發現Eb(Nins-LaAlO3)

表1 N摻雜前后LaAlO3的生成焓、結合能和自旋極化能Table 1 Enthalpy of formation, cohesive energy and spin polarization energy of N-doped LaAlO3

3.2 缺陷形成能

為進一步研究N摻雜LaAlO3結構的穩定性，計算了摻雜體系的形成能。對Nsub-LaAlO3模型，其形成能計算公式如下[12,21]：

Eform=Etot(N-doped)-[Etot(pure)+μN-μO]

(3)

對Nins-LaAlO3模型，其形成能計算公式如下：

Eform=Etot(N-doped)-[Etot(pure)+μN]

(4)

式中Etot(N-doped)和Etot(pure)分別為N摻雜后和未摻雜的LaAlO3晶胞總能量， N和O原子的化學勢分別為μN和μO。考慮生長條件對形成能的影響，即分別在氧化狀態下和還原狀態下形成能。在氧化狀態下，O原子的化學勢取基態氧分子的能量，即μO=μO2/2；對N原子，其化學勢取自N的最高穩定化合價的氧化物，即NO2分子與氧分子O2的差值，即μN=μNO2-μO2。在還原狀態下，替位摻雜時，考慮到化學方程式：

LaAlO3+(x/2)N2→LaAlO3-xNx+(x/2)O2

(5)

式中的x為摻雜的N原子的個數。所以對O原子，其化學勢依然取基態氧分子的能量，即μO=μO2/2。

計算結果如圖2所示，表明替位摻雜和間隙摻雜體系在還原狀態下的形成能更低，即在還原條件下更能實現N摻入LaAlO3中。且對比替位摻雜的形成能比間隙摻雜的形成能更低，即在制備過程中，N更多以替位而非間隙形式存在。

圖2 N摻雜LaAlO3的形成能 Fig.2 Formation energy of N-doped LaAlO3

圖3 不同N源摻雜LaAlO3的形成能 Fig.3 Formation energy of doped LaAlO3 with different N source

基于以上結論，繼續探討不同的N源對摻雜的影響。分別以NH3和N2為N源時，替位摻雜時形成能計算方程式分別為：

LaAlO3+(x/2)N2→LaAlO3-xNx+(x/2)O2

(6)

LaAlO3+x(NH3)→LaAlO3-xNx+xH2O+(x/2)H2

(7)

定義以NH3和N2為N源時，間隙摻雜時形成能計算方程式分別為：

LaAlO3+(x/2)N2→LaAlO3Nx

(8)

LaAlO3+x(NH3)→LaAlO3Nx+(3x/2)H2

(9)

其中x為氮源的個數，計算結果如圖3所示，表明對替位摻雜而言，NH3源的形成能更低，更容易摻雜；對間隙摻雜而言，N2源的形成能更低，更容易形成摻雜。綜上，發現以NH3為N源制備的N替位摻雜LaAlO3的形成能最低，最易合成LaAlO3-xNx。

3.3 電子結構

Nsub-LaAlO3體系和Nins-LaAlO3體系的總態密度(DOS)以及La、Al、O、N原子的分波態密度(PDOS)如圖4所示。從圖4(a)看出，在Nsub-LaAlO3體系中能量E=0即費米面附近自旋向上和自旋向下的態密度不相等，具有明顯的劈裂現象，說明Nsub-LaAlO3體系中對外表現出凈磁矩，呈現鐵磁性。從分波態密度圖可發現N原子的2p電子態與O原子的2p電子態在費米面附近具有明顯的重疊現象，說明N-2p電子態與O-2p電子態產生了雜化，形成共價鍵，該雜化耦合作用導致費米面附近的能級退簡并，從而使得能量E=0附近的自旋向上和自旋向下的態密度不相等，Nsub-LaAlO3體系因此產生鐵磁性；即Nsub-LaAlO3體系的鐵磁性源于雜質N原子的2p電子與價帶頂O原子的2p電子間的類似p-d耦合的p-p耦合作用。一個氮原子替位一個氧原子產生的總磁矩為1.00 μB，相應的自旋電子密度分布圖如圖5(a)所示。

從圖4(b)看出，在Nins-LaAlO3體系中，同樣地，在費米面附近自旋向上和自旋向下的態密度不相等，具有明顯的劈裂現象，說明Nins-LaAlO3體系中電子間的耦合作用使得自旋排列出現有序，體系對外表現出凈磁矩，呈現鐵磁性。同樣從分波態密度圖也可發現自旋密度局域在摻雜的N離子本身以及鄰近的O原子上，說明Nins-LaAlO3體系的磁矩可歸結為N-2p電子態與O-2p電子態間的耦合作用。由于LaAlO3體系的價帶頂部由O-2p態電子構成，而雜質N-2p電子態的對稱性以及波函數均與O-2p電子類似，所以在費米面附近O-2p和N-2p電子態會發生p-p耦合，使得2p軌道分裂，進而使得自旋向上和自旋向下的態密度不相等，體系產生鐵磁性。每個N原子間隙摻雜產生1.00 μB的總磁矩，相應的自旋電子密度分布圖如圖5(b)所示。

圖4 N摻雜LaAlO3體系的電子總態密度及部分原子的分波態密度圖 (a)N替位摻雜LaAlO3;(b)N間隙摻雜LaAlO3 Fig.4 Total and partial density of states of N-doped LaAlO3(a)Nsub-LaAlO3;(b)Nins-LaAlO3

圖5 N摻雜LaAlO3體系的自旋電子密度分布圖 (a)N替位摻雜LaAlO3;(b)N間隙摻雜LaAlO3 Fig.5 Spin electron density distribution of N-doped LaAlO3 (a)Nsub-LaAlO3;(b)Nins-LaAlO3

4 結 論

采用第一性原理計算方法，研究了Nsub-LaAlO3和Nins-LaAlO3的穩定性和電子結構，發現二者都具有穩定的結構，且Nsub-LaAlO3穩定性比Nins-LaAlO3更高；形成能表明在還原條件下，Nsub-LaAlO3比Nins-LaAlO3更容易制備。電子結構表明Nsub-LaAlO3和Nins-LaAlO3體系均具有鐵磁性，其磁性均源于雜質N原子2p電子與價帶頂O原子2p電子間的p-p耦合，計算結果給制備鐵磁性LaAlO3氧化物材料提供了理論指導。